基于DOE、RSM及PSO的大尺寸板类塑件的翘曲优化

刘月云， 刘碧俊

(江苏食品药品职业技术学院机电工程学院，江苏 淮安 223005)

0 前言

注射成型具有成型周期短、生产效率高、易实现自动化生产等特点，目前半数以上塑件是注射成型生产的[1]。在大尺寸平板及类平板塑件的注塑过程中经常出现翘曲变形，翘曲变形过大会影响产品的装配、合格率及使用寿命。影响塑件翘曲的因素较多，有塑件结构、模具设计及工艺参数等。在实际生产中塑件及模具结构已经确定，如果轻易更改则会增加成本、降低效率，所以通过优化工艺参数来减少翘曲变形是较为有效的方法[2]。本文以柜式空调面板为研究对象，首先通过DOE分析出影响塑件翘曲变形的主要工艺参数，再利用RSM构建出翘曲量与主要工艺参数之间的响应面模型，最后运用PSO对响应面模型进行迭代寻优，获得柜式空调面板翘曲量最小的最优工艺参数。

1 模型建立与DOE分析

1.1 模型建立

柜式空调面板的形状规则，正面为光面，背面布置有加强筋，塑件最大外形尺寸为490 mm×400 mm，壁厚为3 mm，中间仪表孔尺寸为360 mm×80 mm。将塑件三维模型导入到Moldflow软件中进行网格划分、诊断和修复。将网格最大纵横比降为6，消除模型中的自由边、多重边、配向不正确单元和相交单元等缺陷，网格的匹配率达96.5 %，满足分析要求。

根据塑件尺寸大小及结构特点，在模型中间仪表孔处设置4个平缝浇口进料，平缝浇口的尺寸为40 mm(宽)×1.5 mm(厚)×1.5 mm(高)。浇注系统中主流道尺寸为：始端直径5.5 mm，末端直径8 mm，长55 mm；分流道直径为8 mm。

在模具的型芯板和型腔板内分别布置冷却水道，水道直径为12 mm，水道数18个；水道与零件间距离为30 mm，水道中心距为30 mm，塑件之外距离为30 mm。

柜式空调面板材料选用LG Chemical公司牌号为HIPS 60HR的抗冲击性聚苯乙烯(PS-HI)，PS-HI具有刚性好、易成型及着色性能好等优点，被广泛用于家用电器、仪器仪表和玩具用品[3]。

1.2 DOE分析

Moldflow中的DOE模块是通过设计一系列的实验，用最少数量的实验完成所有参数在不同水平上的全部实验，并确定出各个参数变量对质量指标的影响程度[4-5]。

影响塑件注射成型质量的因素较多，本文在研究时选择尽量多的工艺参数进行实验，如熔体温度、模具温度、注射压力、注射时间、保压压力、保压时间、冷却时间等，选取翘曲变形作为质量指标。

工艺参数的范围以Moldflow材料库推荐的工艺参数为中间值，进行上下浮动。定义所有工艺参数对质量指标的影响程度总和为100 %，占百分比越高，则该工艺参数对质量指标的影响程度就越大。运用DOE进行设计、分析，得到工艺参数对柜式空调面板翘曲变形的影响程度如表1所示。

表1 工艺参数对翘曲变形的影响程度Tab.1 Influence of process parameters on warpage

从表1可以看出，对柜式空调面板翘曲变形影响较大的工艺参数有熔体温度、模具温度、保压压力和保压时间，其中保压压力的影响最大，达到36.87 %，然后分别是模具温度的29.48 %和熔体温度的23.13 %，保压时间的影响最小，影响程度为8.13 %。除这4个工艺参数之外，其他工艺参数对翘曲变形的影响程度总和为2.39 %，影响较小，可以忽略不计。

2 响应面实验

2.1 实验方案与结果

RSM是利用合理的实验设计采用多项式函数来拟合实验因素与响应值之间的函数关系，并通过对回归方程的分析来寻求最佳工艺参数，是解决多变量问题的一种统计方法[6]。

在RSM设计时，以柜式空调面板注塑时的翘曲量作为响应值，以DOE分析出的对翘曲变形影响较大的熔体温度、模具温度、保压压力和保压时间为实验因素。采用4因素5水平的组合来进行RSM实验中的中心复合设计(CCD)实验规划，并根据塑件的外形尺寸、壁厚以及PS-HI的推荐工艺参数来选取4个实验因素的实验水平，具体的实验因素、水平及编码如表2所示。

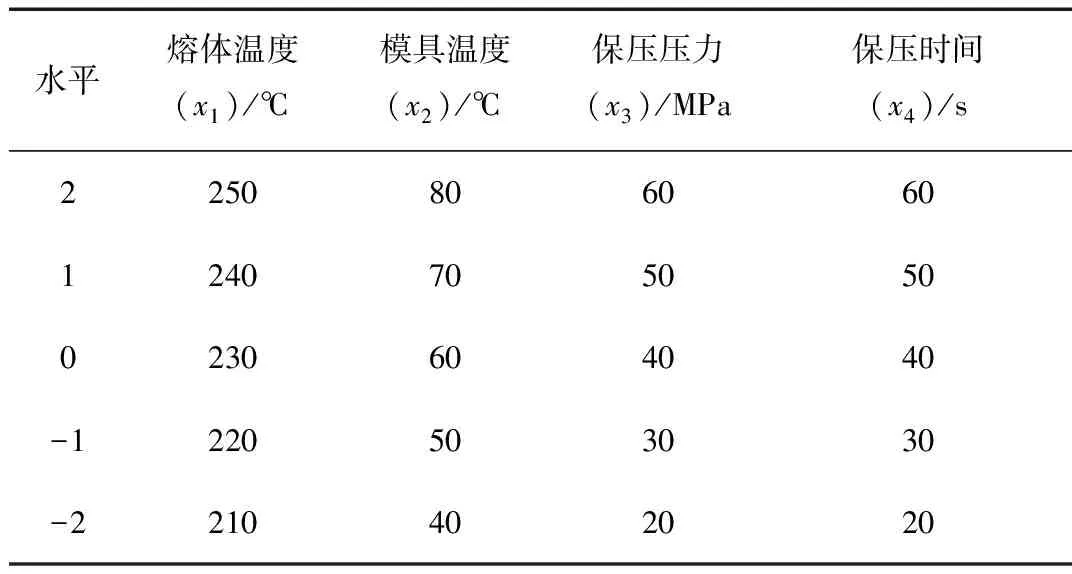
表2 响应面实验因素、水平及编码Tab.2 Response surface experimental factors, levels and coding

CCD需进行的实验次数为：

2n+ 2n+m

(1)

式中n——因素的个数

2n——角点实验数

2n——轴点实验数

m——中心点处的重复实验数

当n= 4时，角点实验数为16，轴点实验数为8，中心点处的重复实验数为6，共计30组响应面实验，具体的实验方案与对应的翘曲量如表3所示。

表3响应面实验方案与结果

Tab.3 Response surface experimental scheme and results

实验编号x1x2x3x4y11-11-15.6722-1-1-1-16.79931-1-116.916400006.26950-2006.1796-20006.4747-1-1-116.945811-116.689900006.2691000006.2691100006.2691200026.29013000-25.886141-1115.67915-1-11-15.8631611-1-16.3651700-207.984181-1-1-16.73419-11115.8892000205.65921-11-116.8752200006.2692320005.98724-11-1-16.53725-111-15.66026111-15.4472702006.1162811115.6602900006.26930-1-1116.010

2.2 响应面模型建立

响应面模型能够用来建立实验因素和响应值之间的函数关系，塑件的翘曲量与工艺参数之间是非线性关系，描述这种非线性关系常用二阶多项式的响应面模型，其数学表达式为：

(2)

式中y(x)——翘曲响应目标函数

x——工艺参数

α——各项系数

k——待优化工艺参数个数

以式(2)的函数为理论基础，根据表3的实验数据，运用Design-Expert软件进行多项式回归拟合分析，得到的二次响应面模型为：

y(x)=10.352 56+0.035 306x1-0.100 43x2-0.025 631x3-0.092 991x4+4.145 85×10-4x1x2-5.067 00×10-4x1x3+4.458 35×10-4x1x4+3.830 01×10-5x2x3+9.183 35×10-4x2x4-4.329 50×10-4x3x4-1.548 61×10-4x12-3.623 61×10-4x22+1.322 64×10-3x32-5.111 11×10-4x42

(3)

式中y——塑件最大翘曲量，mm

x1——熔体温度， ℃

x2——模具温度， ℃

x3——保压压力， MPa

x4——保压时间，s

2.3 方差分析

运用Design-Expert软件对实验数据进行方差分析，得到的结果如表4所示。“平方和”表示每一个系数值平方的和，这些值是用来衡量每个系数的可变性对数据的获得所作的贡献。自由度则表示会诱导错误预测的系数个数[7]。“P值”为大于“F值”的概率，“P值”小于0.05时，代表此模型项显著，即对响应的影响大。从分析结果发现x1、x2、x3、x32都是模型的显著项，保压压力对翘曲变形影响最为显著(P<0.000 1)，模具温度(P=0.003 1)和熔体温度(P=0.007 7)的影响也较为显著，而保压时间对翘曲变形的影响不显著，这与DOE的分析结果一致。响应面模型的“F值”为12.18，模型显著，意味着模型在统计学上是有意义的，仅有0.01 %的概率会产生噪音。失拟项的“F值”为0.33，这相对于纯误差并不显著，表明模型的拟合度较高。

表4 方差分析结果Tab.4 Analysis of variance

2.4 模型检验

在运用构建好的响应面模型对工艺参数进行优化求解之前，首先通过残差分析来检验模型的准确性及合理性。经过分析所得的残差正态概率如图1所示，从图中可以发现残差序列点基本位于一条直线上，这说明残差呈现正态分布，满足最小二乘拟合方法的要求。而残差与拟合值分布如图2所示，可以看出残差序列点分布较分散，随机性较好。残差序列点的正态性、随机性充分证明了响应面模型是准确和合理的。

图1 残差正态概率图Fig.1 Residual normal probability graph

图2 残差与拟合值分布图Fig.2 The residual and fitted value distribution

以上分析表明根据CCD实验数据所构建的响应面模型较好，能够很好地运用于拟合塑件工艺参数对翘曲变形的影响研究。

2.5 工艺参数的RSM优化

以柜式空调面板翘曲量最小为目标，根据构建的响应面模型对4个工艺参数进行优化，得到最小翘曲量为5.351 mm，对应的工艺参数为：熔体温度237.26 ℃、模具温度61.40 ℃、保压压力54.82 MPa、保压时间20.77 s。

图3 工艺参数经RSM优化后的翘曲变形Fig.3 Warpage of process parameters optimized by response surface method

运用以上工艺参数对塑件模型进行模流分析，得到的翘曲变形情况如图3所示。从图3可以看出，塑件中心部位的翘曲变形较小，四周的翘曲变形较大，最大翘曲量为5.271 mm，与由响应面模型优化得到的最小翘曲量5.351 mm相比，误差仅为2.486 %，响应面模型的预测及优化效果较好。

3 粒子群优化

3.1 工艺参数的PSO优化

PSO是模拟鸟群随机搜寻食物的捕食行为，因算法简单、收敛迅速、全局搜索能力强等优点被广泛应用于求解多目标优化问题，并取得了较好的效果[8]。

以式(3)的响应面模型作为适应度函数，将4个工艺参数的实验取值范围作为约束条件，具体约束条件为：210≤x1≤250，40≤x2≤80，20≤x3≤60，20≤x4≤60。

以适应度值为函数值，将函数的最小值作为寻优目标，对熔体温度、模具温度、保压压力和保压时间等4 个工艺参数进行优化。

PSO的参数设置为：惯性权重ω=0.8，c1=c2=2，种群粒子数为30，算法迭代次数为100次，精度为0.001。利用Matlab软件编写PSO程序并运行，经过100次迭代寻优，PSO最优个体适应度值变化如图4所示。

图4 PSO最优个体适应度值变化情况Fig.4 The optimal individual fitness value of PSO

图5 工艺参数经PSO优化后的翘曲变形Fig.5 Warpage after optimization of process parameters by PSO

从图4可以看出，目标函数在迭代30次左右时已经达到最小，最小值为3.298 mm，对应的工艺参数为：熔体温度241.63 ℃，模具温度60.32 ℃，保压压力56.94 MPa，保压时间18.29 s。将经过PSO优化所得的工艺参数输入Moldflow软件中进行翘曲分析，分析结果如图5所示。从图5中发现柜式空调面板的最大翘曲量为3.459 mm，与计算值3.298 mm相比，误差仅为4.882 %，误差较小。

3.2 RSM与PSO优化效果对比

RSM与PSO 2种优化方法的优化结果对比如表5所示，经过PSO优化后的翘曲量的计算值比RSM优化值降低了2.053 mm，降低了38.367 %，而经过模流分析验证后的翘曲量由5.217 mm降至3.459 mm，降低了33.698 %，PSO的优化效果更好。

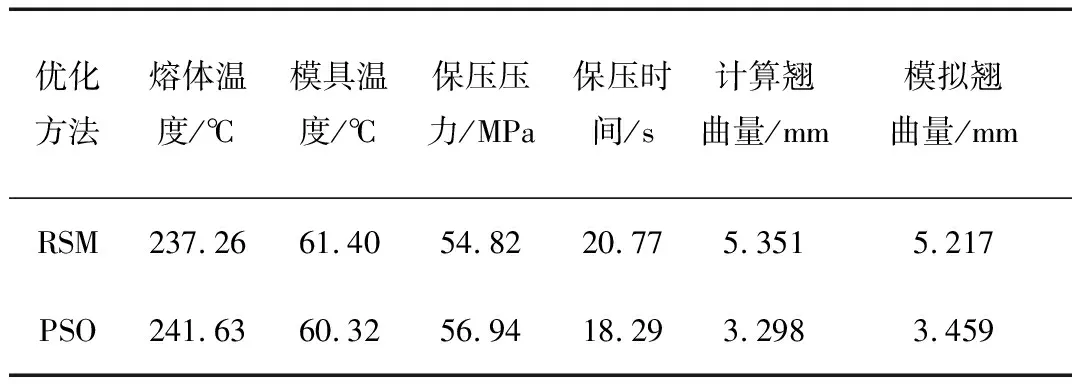
表5 2种优化方法分析结果对比Tab.5 Comparison of the analysis results of two optimization methods

4 结论

(1)利用DOE分析出对柜式空调面板翘曲变形影响较大工艺参数有熔体温度、模具温度、保压压力和保压时间；

(2)以DOE分析出的4个工艺参数为实验因素进行RSM实验设计，并构建出工艺参数与翘曲量之间的响应面模型，优化获得最小翘曲量为5.351 mm，对应的工艺参数为：熔体温度237.26 ℃、模具温度61.40 ℃、保压压力54.82 MPa、保压时间20.77 s，用此组工艺参数验证得最大翘曲量为5.217 mm，误差仅为2.486 %，响应面模型精度高；

(3)运用PSO对响应面模型进行迭代寻优，得出最小值3.289 mm，对应的工艺参数组为：熔体温度241.63 ℃，模具温度60.32 ℃，保压压力56.94 MPa，保压时间18.29 s，验证出最小翘曲量为3.459 mm，与PSO计算值的误差为4.882 %；相比于RSM，PSO优化后的面板模拟翘曲量降低了1.758 mm，降低33.698 %，优化效果较好。