能源混沌系统基于事件触发采样的同步算法

郭白璐，肖小庆

(南通大学 电子信息学院, 江苏 南通 226019)

作为非线性系统的有趣现象，混沌展现了极其复杂的动态行为。由于混沌系统的解对初值极其敏感，使得其长期具有不可预测性。混沌现象出现在许多工程领域，比如，化学工程，生物工程，安全通信，机器人技术等[1]。混沌现象极其相关研究已经受到了极大的关注。其中关于混沌系统同步的研究也引起了许多研究者的兴趣。混沌同步指的是不同混沌系统的状态轨迹运行逐渐趋向一致的现象。目前混沌同步的主要方法有驱动—响应同步方法、主动—被动同步方法、基于相互耦合的同步方法、自适应同步方法等[2]。

另一方面，随着计算机技术、微处理器以及通信技术的发展，离散时间控制器在很多实际应用中获得了广泛的应用，它仅需要在离散时间获得系统测量输出的采样数据。近年来，利用采样数据研究混沌系统同步的问题取得了一些重要的研究成果[3-5]。文献[4]针对一类Lur'e混沌系统，通过将采样同步的误差系统表示为具有时变时延的系统, 并利用自由权矩阵方法给出了系统全局混沌同步控制器的线性矩阵不等式设计方法。在此基础上，文献[5]做出了进一步的改进，得到了可以在更大的采样周期下保证主从系统同步的采样控制器设计方法。

上述基于采样数据的混沌系统同步方法都是基于时间触发的，即传感器对系统输出信号的采样是在预先设定的时刻进行的。由于数据采样没有考虑到系统本身的运行状态，因此时间触发采样方法并不是一种十分有效的采样控制方法。为了减少不必要的数据传输，人们提出了一种有效的采样控制方法—事件触发采样方法[6-7]，即设计合适的事件触发机制，产生比较大的变化时才对系统进行采样的一种方法。实验表明，与时间触发采样方法相比，事件触发方法可以在减少系统对资源占用的同时获得所期望的性能[8-10]。针对由混沌动力学模型表示的能源系统[11]，本文基于事件触发采样方法，研究了其渐近同步的事件触发控制方法，并且基于Matlab软件提出了能源混沌系统的事件触发采样同步算法设计。不同于文献[11]中的连续线性反馈控制律，本文采用的是基于事件触发采样数据的离线反馈控制律，在减少数据传输的同时也能够使得主从系统较快的达到同步。最后，利用Matlab软件通过数值仿真说明了所给算法是有效的。

1 能源混沌系统的事件触发采样同步模型

本文考虑由下面的混沌动力学模型所表示的能源系统[8]

(1)

其中，a1=0.09,a2=0.15,

b1=0.06,b2=0.083,b3=0.07,c1=0.2,

c2=0.5,c3=0.4,M=1.8,N=1.0.令：

a3=a1/M,b4=b3N,d1=c1c2,d2=c1c3,则系统(1)改写为：

(2)

考虑基于事件触发采样的混沌系统同步问题，从系统为:

(3)

其中u1,u2,u3为待设计的同步控制输入。

设同步误差状态分别为

则由(1)和(3)得到如下同步误差方程

(4)

在不考虑数据采样的情形下，文献[11]设计了连续线性反馈控制律：

u1=-ge1,u2=-ge2,u3=-ge3，

当g充分大时, 所设计的控制器可以使得系统(1)和(3)达到全局指数渐近同步。

本文考虑如图1所示的基于事件触发采样的同步模型, 同步反馈控制律:

ui(t)=-kiei(tk),i=1,2,3,t∈(tk,tk+1) (5)

其中tk为事件触发采样时刻。

图1 混沌系统的事件触发采样同步模型
Fig.1 Event-triggered sampling synchronization model of chaotic systems

记同步误差向量为

e(t)=[e1(t)e2(t)e3(t)]T，

反馈控制增益矩阵为K=diag(k1,k2,k3).

定义事件触发采样时刻tk如下:

(6)

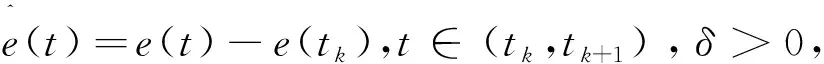
注1：本文考虑的基于事件触发采样的同步方法，采样时刻由事件触发条件(6)得到，即只有满足触发条件(6)的时刻才进行采样，从而可以在一定程度上减少不必要的数据采样。

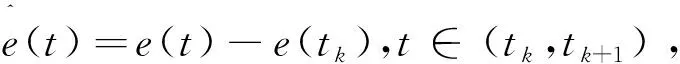
(7)

2 能源混沌系统的事件触发采样同步分析

由上述分析可知，能源混沌系统(1)的同步问题等价于同步误差系统(7)渐近稳定的问题。接下来我们利用李雅普诺夫稳定性理论给出充分条件使得同步误差系统(7)是渐近稳定的。

选择李雅普诺夫函数

V(e(t))=eT(t)Pe(t).

当t∈[tk,tk+1)时，计算V(e(t))沿着误差系统(7)的状态轨线关于时间的导数得到:

e1[a1e1-a2(e2+e3)-a3x2+

e2[b4e1-b1e2-b2e3-b3(x-z)+

(8)

由于混沌系统的轨线是有界的，于是存在正常数c使得:

(9)

注意到事件触发条件(6)的定义, 可知当t∈[tk,tk+1)时,

将上式代入(9)中, 有：

P[|e1(t)||e2(t)||e3(t)|]'+δ‖e(t)‖2≤

-(λ-δ)‖e(t)‖2,t∈(tk,tk+1)

其中:

P=

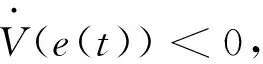
3 能源混沌系统的事件触发采样同步算法设计

(1)选择控制器参数ki，使得矩阵P为正定矩阵。通过命令eig(P)求P的特征值，验证P是否为正定矩阵。

(2)计算P的最小特征值λ=λmin(P)>0，选取事件触发参数δ∈(0,λ).

(3)由上述所得的控制增益矩阵K，以及事件触发规则(6)，通过Matlab软件编写相应程序进行仿真验证。

4 数值仿真

通过Matlab软件进行仿真以说明所给同步算法是有效的。选取系统(1)和(2)的初值分别为(0.1,0.2,0.5)和(2,1,-3).通过Matlab软件进行仿真可得能源混沌系统(1)的轨线的界c=37.

(1)将c=37代入矩阵P，选取控制器参数分别为k1=10,k2=12,k3=6，计算P的特征值分别为 0.786 2，5.768 3及14.095 6，显然P是正定的。

(2)λ=λmin(P)=0.786 2，由此得到事件触发参数的取值范围为δ∈(0,0.786 2).

(3)利用所得控制增益矩阵K，选取事件触发参数δ=0.75，利用Matlab仿真对同步结果进行进一步的分析。

由图2也可以很明显的看出能源系统与其从系统均呈现混沌状态，具有类似的混沌吸引子。基于事件触发的采样间隔如图3所示。利用所给的事件触发机制，同步误差状态均快速收敛到0，能源混沌系统及其从系统之间的误差状态的仿真图形如图4所示。

5 结论

针对能源混沌系统，利用事件触发采样方法，设计了能源混沌系统的同步模型。根据李雅普诺夫稳定性理论得到了系统同步的充分性条件。并基于Matlab软件，给出了同步算法设计。仿真结果说明所给的算法容易实现，而且同步的效果较好，同时减少了数据的采样次数。利用本文类似的方法也可以解决蔡氏混沌系统、洛伦兹系统等混沌系统的同步问题。

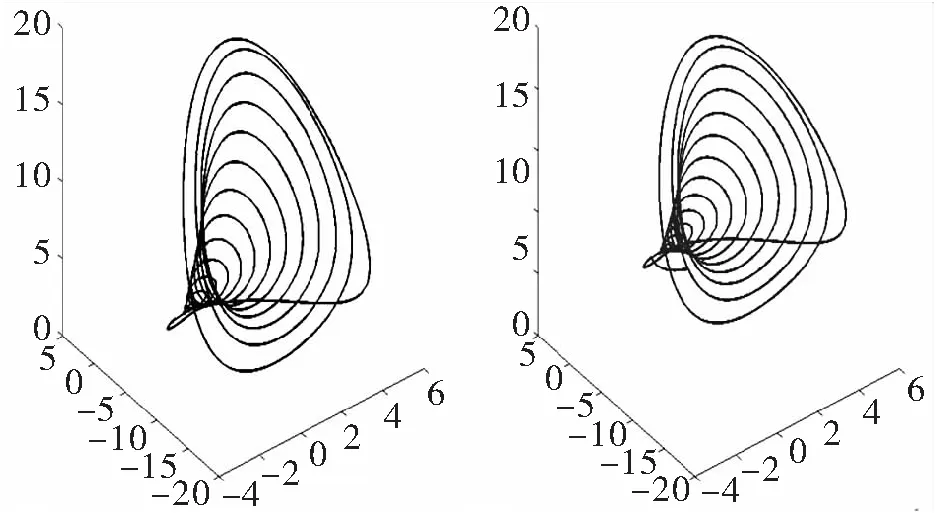
图2 混沌吸引子
Fig.2 Chaotic attractor

图3 事件触发采样间隔
Fig.3 Event-triggered sampling interval

图4 同步误差状态
Fig.4 State of synchronization error