基于不同材料的汽车车轮的模态分析

苏仕见，徐元利，张泽豫

（1.天津科技大学机械工程学院，天津 300222；2.中国汽车技术研究中心汽车工程研究院，天津 300300）

前言

车轮是汽车行驶系统中的重要部件，起着承载、驱动、转向和制动等作用，其性能的好坏直接影响汽车操纵的稳定性、行驶安全性、乘坐的舒适性等[1]。为了避免汽车在行驶时车轮发生共振，车轮的振动频率需要避开外部的激励频率。外部激振主要包括发动机的振动频率和路面激励频率。

对于汽车车轮的结构和材料特性对模态、疲劳的影响，有许多学者和工程师进行了卓有成效的探索[2,3]。本文对于相同结构不同材料的车轮的模态分别做了仿真计算，并对其变化规律进行了研究。掌握车轮在不同材料下模态的差异性和变化规律，对提高车轮在不同工况下行驶的稳定性和安全性，进而提高汽车整车的操纵稳定性和乘坐舒适性具有极为重要的意义。

1 车轮有限元模型的建立

1.1 网格划分

将车轮的CAD模型导入HyperMesh划分四面体网格。首先对模型进行几何清理，在不影响计算结果精度的情况下清理掉不必要的倒圆角，以保证生成质量合格的网格；其次是二维网格划分与单元质量检查，此时划分的二维网格将对后面的三维网格划分起引导作用；最后是在Tetra Meshing下划分出四面体三维网格。此次车轮模型的网格划分节点数为17924，单元数为54813。

图1 车轮的有限元模型

1.2 材料参数的设置

本次模态研究主要是对钢、铝合金和镁合金三种材料的车轮进行模态计算及分析，所以分别设置如下三种材料参数。

表1 车轮材料参数

2 模态分析

2.1 模态分析的理论基础

对于一个弹性系统来说，其动力学通用的微分方程为[4]

式中：[M]是质量矩阵；[C]是阻尼矩阵；[K]是刚度矩阵；是加速度向量；是速度向量；[u]是位移向量。

由于在进行模态分析时，汽车车轮结构的固有特性与外部的载荷和激励条件均无关，因此式(1)中=0，而[C]在分析的过程中一般忽略。所以其方程简化为：

由于弹性体的自由振动总可以分为一系列简谐振动的叠加，当发生谐振动时，即时，方程变形为：

式(3)是关于 的n次方程，解方程可得到结构的n个固有频率，每个固有频率都有一个相应的振型向量。

2.2 边界条件

模态分析中有自由模态和约束模态两种边界条件，车轮在实际工况中，轮毂轴承是通过法兰盘轮毂的螺纹孔与螺栓固定联接，所以对轮毂所有的螺栓孔施加全约束。

2.3 模态计算与后处理

对结构进行模态分析时，是为了得到零件的多阶固有频率、振型等。一般不需要求出全部固有频率和振型，应着重考虑车轮在实际工况下所涉及的低阶频率，低频振动往往引起零件的破坏性共振且不易被阻尼消耗[5]。通常也只有这些频率能激励车轮的振动从而引起共振。因此，选择车轮的前八阶模态进行分析。

将车轮有限元模型导入 MSC.Nastran软件进行模态计算，然后将计算结果导入HyperView进行数据后处理。模态计算后得到的三种不同材料的车轮的前八阶模态的振型基本相同，振型图如图2所示。

图2 车轮前八阶模态振型图

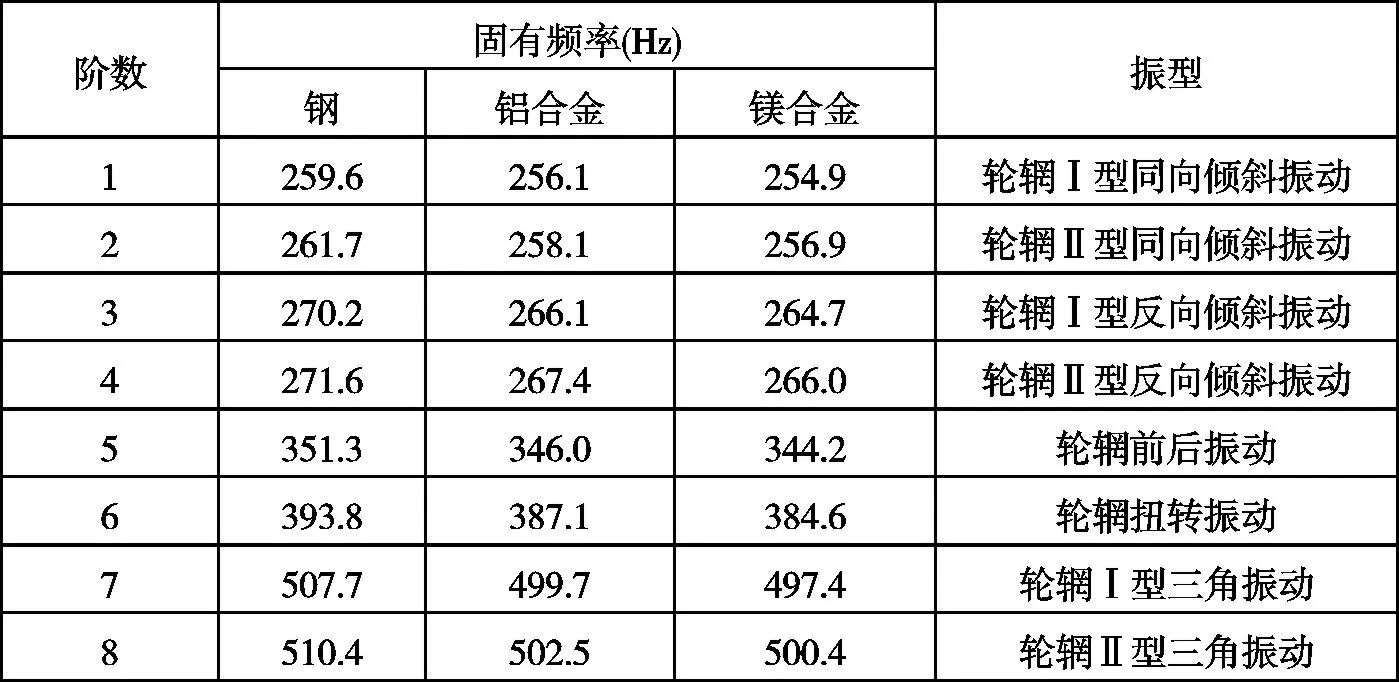
表2 三种材料车轮的前八阶模态

钢、铝合金和镁合金车轮前八阶模态的数值见表 2。从表中可以看出，该车轮在三种不同材料属性条件下的各阶固有频率数值非常接近， 说明相较于车轮的结构，材料对模态的影响较小。

3 模态计算结果分析

3.1 外部激励频率

（1）路面激励频率

高速公路和城市较好的路面，路面激励频率一般在3Hz以下，凹凸不平路面或者乡村路面激励频率一般低于11Hz。

（2）发动机激励频率

四缸发动机在怠速下振动频率范围一般为 23-40Hz；启动后在最高转速下的振动频率为200Hz左右。

因此，该车轮在三种不同材料下的各阶固有频率均远离发动机振动频率和路面激励频率，即此车轮将不会被外部激励源激励而引起共振。

3.2 不同材料属性下车轮固有频率变化规律分析

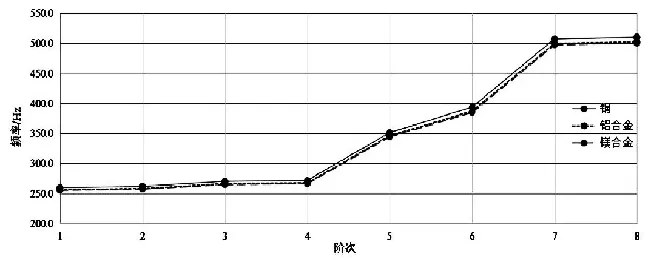
图3 钢、铝合金和镁合金车轮固有频率对比曲线

钢、铝合金和镁合金车轮固有频率对比曲线见图 3。从图中可见，材料为钢的车轮的固有频率相对于材料为铝合金和镁合金的稍偏高一些；铝合金和镁合金材料属性的车轮的固有频率数值基本接近；三种不同材料下此车轮的固有频率各阶次的变化规律基本一致。所以可以得出结论：材料属性对车轮的固有频率影响不大。

4 结论

此次模态计算得到了该车轮结构的前八阶固有频率和振型，可以体现出车轮的结构特性；在前期的设计过程中对车轮进行模态分析，可以有效地避开共振区，为进一步动态分析和优化设计奠定了基础，也为实验研究提供了参考；通过对比分析，发现三种不同材料下该车轮的各阶次固有频率变化规律基本一致，而且固有频率的数值也非常接近，说明材料属性对车轮的模态影响不大。