基于新型趋近律的PMSM超扭曲滑模直接转矩控制

仉 毅，闻振璇，张兴军，王 亮

(1.山东科技大学，青岛 266590；2.山东能源集团山东新巨龙能源有限责任公司，菏泽 274900 )

0 引 言

永磁同步电动机(以下简称PMSM)以其高功率密度、高效率以及高可靠性等优点，在电动汽车、机器人和工业控制等领域具有广阔的前景[1]。然而，PMSM的非线性、强耦合等特性决定了其必须采用先进控制策略如自适应控制、神经网络控制、滑模控制等解决控制系统的非线性、自适应能力差等问题[2]。

直接转矩控制(以下简称DTC)是在矢量控制之后发展起来的，它的控制变量是定子磁链和转矩，不需要进行矢量变换等复杂的运算，且结构简单，动态响应好[3]。虽然传统DTC结构简单，对于参数摄动控制效果好，但是磁链和转矩波动较大，低速时更加难以控制，对系统精度和稳定性控制影响很大[4]。为了解决这些问题，国内外学者提出了诸多的方法，参考文献[5-6]通过增加电压矢量，进而改进开关，但并不能彻底解决引起转矩脉动的问题。文献[7-11]将空间矢量调制(以下简称SVPWM)引入到DTC中，研究表明，此方法对抑制磁链和转矩脉动有较好的效果，而且能够彻底解决逆变器开关频率不稳定的问题。

滑模变结构控制因其鲁棒性强，响应迅速，以及对外界扰动不敏感而备受关注[12]，超扭曲滑模变结构控制论是在高阶滑模的基础上发展而来的，该控制方案具有较好的鲁棒性和动态特性。本文将超扭曲滑模控制方案引入基于到SVPWM的PMSM-DTC系统中,同时用饱和函数sat(s)取代符号函数sgn(s)，改进了滑模控制的趋近律。由于饱和函数变化曲线平滑，当系统状态点远离切换面时，趋近的速度会大大增加；当系统状态点靠近切换面时，趋近的速度能够缓慢下降。调节控制器的参数，能够使函数工作在线性空间，从根本上解决开关切换的问题，消除了滑模控制中的抖振问题，使系统鲁棒性显著提高[13]。

1 PMSM数学模型

1.1 PMSM在静止坐标系下的数学模型

定子电压方程：

(1)

定子磁链方程：

(2)

电磁转矩方程：

(3)

电机运动方程：

(4)

式中：uα,uβ为定子电压的α，β轴分量；iα，iβ为定子电流的α，β轴分量；Ls，Rs为定子电感和定子电阻；ωe为电机的电角速度；φf为永磁体磁链；θe为位置角；p代表磁极对数；J为转动惯量；B为阻尼系数；TL为负载转矩。

1.2 PMSM在旋转坐标系下的数学模型

定子电压方程：

(5)

定子磁链方程：

(6)

电磁转矩方程：

(7)

式中：ud，uq为定子电压的d，q轴分量；id，iq为定子电流的d，q轴分量；φd，φq为定子磁链的d，q轴分量；Ld，Lq为电感的d，q轴分量。

2 基于超扭曲的滑模变结构控制

2.1 滑模控制器的设计

对于一个动态系统，如下：

(8)

式中：x∈Rn为状态变量；u∈R为控制输入量；y为被控制量的输出；A,B,C为未知函数。

滑模变量的一阶、二阶导数如下：

(9)

(10)

则定义二阶滑模如下：

(11)

超扭曲算法表示如下：

(12)

式中：Kp>0，Ki>0,Kp,Ki为增益；滑模变量s=y。

该控制算法不需要滑动变量的导数，滑模面的收敛性和稳定性的充要条件是增益要足够大[15]：

(13)

式中：CM≥|C|，并且DM≥D≥Dm。同时C和D由y的二阶导数所定义：

(14)

在旋转坐标系下的PMSM矢量模型中，定义式(14)中C=ωeφf-Rsid，D=1，因为电机的电流与转速有限制，则满足式(13)。

定义定子磁链的滑动变量表达式：

(15)

式中：φr是定子磁链。

由超扭曲算法可知，定子磁链滑模控制器的表达式：

(16)

式中：Kp，Ki满足式(13)的收敛性条件。

同样电磁转矩的滑动变量表达式：

(17)

则电磁转矩滑模控制器的表达式：

(18)

2.2 新型趋近律滑模控制器

传统超扭曲算法采用的切换函数sgn(s)是一种不连续型函数，会导致系统出现抖振现象。这里引入饱和函数sat(s)取代函数sgn(s)，不仅能保证切换函数的开关特性，同时还能减小抖振和系统的不连续。由于sat(s,δ)·s与sgn(s,δ)·s的符号特性相同，故同样满足稳定性与收敛性条件。

饱和函数sat(s,δ)的表达式：

(19)

式中：δ为较小的正常数，但不宜过小。如果δ取值太小，则会导致抖振问题。所以改进后的定子磁链控制器：

(20)

改进后的电磁转矩控制器：

(21)

3 仿真与分析

借助MATLAB /Simulink仿真工具，对传统PMSM-DTC系统与本文方法进行仿真对比分析。传统PMSM-DTC系统控制框图如图1所示；基于新型趋近律的超扭曲滑模的PMSM-DTC系统控制框图如图2所示。

图1 PMSM-DTC系统控制框图

图2 基于新型趋近律的超扭曲滑模的PMSM-DTC系统控制框图

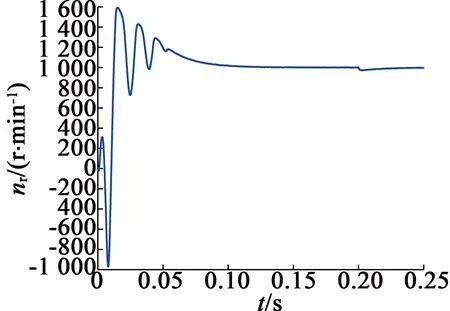
图3 PMSM-DTC系统转速响应图

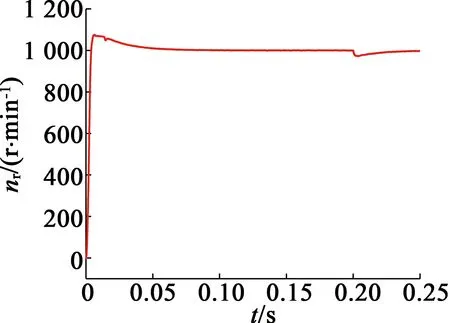
图4 基于新型趋近律的超扭曲滑模的PMSM-DTC系统转速响应图

图5 PMSM-DTC系统转矩响应

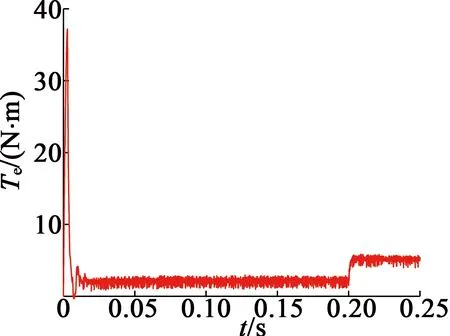
图6 基于新型趋近律的超扭曲滑模的PMSM-DTC系统转矩响应图

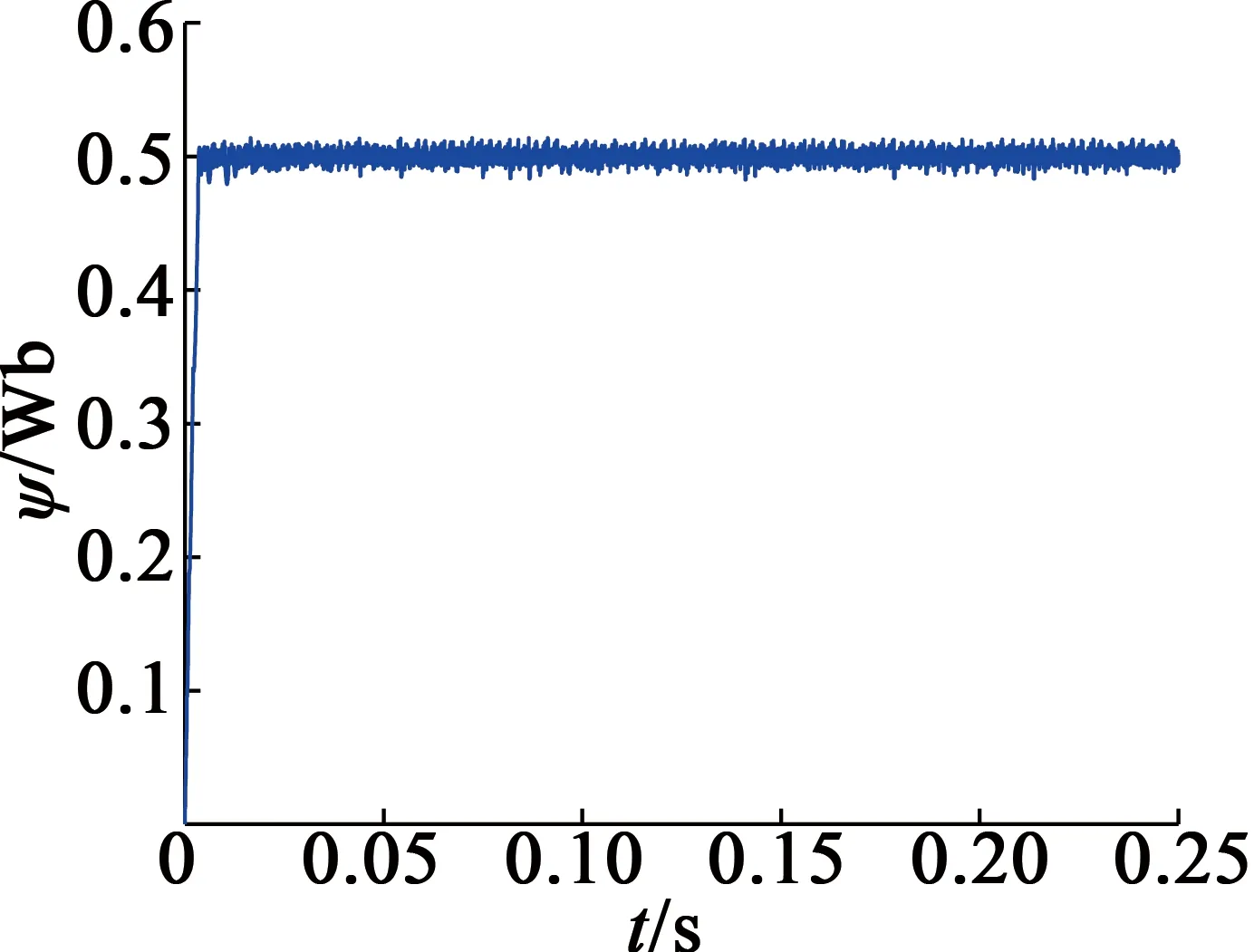
图7 PMSM-DTC系统磁链响应图

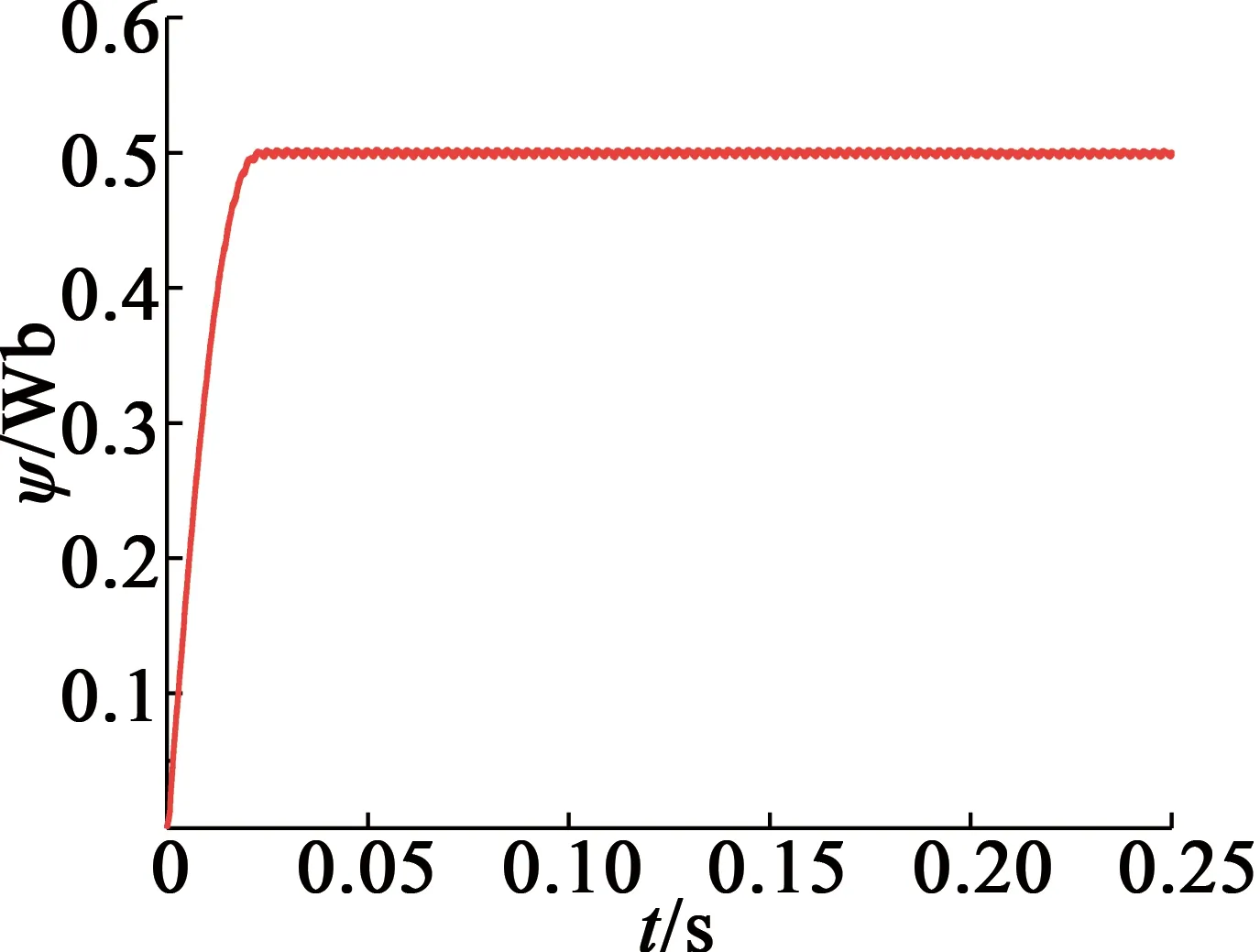
图8 基于新型趋近律的超扭曲滑模的PMSM-DTC系统磁链响应图

电机转速设定为1 000 r/min,在t=0时负载转矩为0.5 N·m，t=0.2 s时其阶跃为5 N·m，2种方法的转矩响应波形对比如图9所示。传统PMSM-DTC系统转矩稳定时间为0.06 s,而改进后系统转矩稳定时间为0.02 s，响应时间减小了0.04 s。同时，改进后转矩脉动明显减小，系统的稳定性得到了显著的提高。

图9 系统转矩响应对比图

2种方法的转速响应波形对比如图10所示。传统PMSM-DTC系统转速稳定时间为0.10 s,而改进后系统转速稳定时间为0.04 s，响应时间减小了0.06 s，同时改进后的转速波动较小，能够快速达到稳定状态。以上分析说明了改进后的系统优于传统的PMSM-DTC系统。

图10 系统转速响应对比图

4 结 语

本文在PMSM-DTC基础上，采用超扭曲结构设计了磁链和转矩的滑模控制器，采用饱和函数sat(s)代替传统方法中的符号函数sgn(s)，并且利用MATLAB/Simulink仿真工具进行仿真分析。仿真结果表明，改进后控制系统速度响应比传统PMSM-DTC系统速度响应在时间上减小了0.06 s，能在更短的时间内使速度趋于稳定。同时对转矩的突变有较好的鲁棒性，转矩脉动更小，系统的稳定性优于传统的PMSM-DTC系统。