基于温升曲线的电机过载控制研究
张豫南,史浩楠,杨怀彬,房 远,董 政
(陆军装甲兵学院,北京 100072)
0 引 言
履带式全方位地面平台从根本上解决了全方位车辆通过性能的问题,兼顾传统全方位平台的机动灵活性与履带车辆的复杂路面越野能力,具有很高的军事及民用前景。但复杂的越野环境对车辆电机的负载能力提出了更高的要求[1],如果选用大功率电机将不可避免增加平台质量,甚至影响整车设计;同时电机多数状况下工作在平地运行状态,选用大功率电机造成了电机资源的浪费。基于平台的特殊应用要求,本文提出一种基于一定过载倍率下电机温度特性曲线的电机控制方法,当平台工作在爬坡工况时,在不损坏电机的情况下,一定时间内大扭矩输出,最大限度地提高了电机的过载运行能力,同时降低了车身重量,提高了电机利用效率。
1 匹配计算与方案提出
履带式全方位地面平台的主要性能指标如表1所示。

表1 平台主要结构参数
若不考虑某些极端情况,当平台爬坡角度αm=32°时,电机达到最大持续输出功率:
(1)
式中:μs为地面滚动摩擦阻力系数,取0.05;ηch为电机到传动轮的传动效率;ηx为行动装置效率;z为电机数量。
若平台爬坡速度为vm≥5 km/h,由式(1)可得电机的最大持续输出功率:
Pem≥863.36 W
(2)
根据上述计算,平台选用AMETEK公司的IB340006电机,其具体参数如表2所示。

表2 无刷直流电动机主要参数
若要保证平台的最高速度达到25km/h,则电机的减速比:
(3)
式中:rz为履带半径;nmax为电机最高转速。计算可得i0≤20.08。
减速比的下限由电机的最大输出转矩和最大爬坡对应的行驶阻力决定[2]:
(4)
式中:Τm_max为电机的最大输出转矩。如果取Τm_max=2.32N·m(额定扭矩),计算得:i0≥59.48。
根据上述匹配计算,若要达到减速比i0≤20.08,电机必须过载3倍以上运行,但电机持续长时间过载运行将对电机本身产生损害。过载运行对电机的损害主要由电机发热产生,如果将电机始终控制在一定的温度范围内工作,将大大减少过载运行对电机的伤害,提高电机过载运行性能。但无刷直流电动机结构紧密,在电机之内安装温度传感器存在许多困难,基于上述应用实践需求,提出一种基于一定过载倍率下电机温度特性曲线的电机控制方法。
2 理论分析
2.1 热源分析
2.1.1 热源产生
铁耗:
pFe=KαρFeGFe
(5)
式中:Kα为损耗增加系数,与磁通密度的分布硅钢片加工等有关;ρFe为单位质量铁心材料产生的损耗,与铁心材料有关;GFe为铁心的质量。当电机选定时,电机单位时间内铁耗基本为定值。
铜耗:
pCu=3I2R
(6)
在分析电机的铜耗时,为了便于计算,通常认为绕组截面上的电流为均匀分布,故可将式(6)中的电阻看作直流电阻进行计算。
机械损耗是电机运行过程中产生的,相较于铜耗、铁耗,机械损耗较小,且因不同电机安装运行过程难以定量计算,故一般在分析时忽略不计。
2.1.2 电机散热
电机的散热过程主要是电机与周围物质的热交换,根据傅里叶提出的导热基本定律可知[3-4]:
q=λA(T-T0)
(7)
式中:q表示热流密度;λ表示导热系数;A表示物体与周围环境接触面积;T-T0表示温度梯度。当电机确定时,电机结构、材料等随之确定,当到达某一温度时电机导热系数不变,由傅里叶导热定律可知,当温度梯度确定时,电机与周围环境的热交换速度不变。
2.2 电机热计算
通过上述分析可得当选取某一款电机时,不改变冷却方式,电机单位时间内获得的热量具体可表示:
ΔQ=(pCu+pFe-q)Δt
(8)
式中:ΔQ表示电机增加热量;Δt为电机运行时间。当电机升温时,电机温度场由于多部件结构、导热系数等因素的不同,呈现出强耦合、复杂分布的现象,如果将电机等效为一个单独热源,则电机温升公式可表示:
K0ΔT=(pCu+pFe)Δt-λA(T-T0)Δt
(9)
式中:K0表示等效电机温度系数;T0表示环境温度。式(9)可等效:
(10)
解得:
(11)
将式(11)化简:
T=-K1e-K2t+K1+T0
(12)
当电流一定时,电机温度为时间的指数函数。将式(6)代入式(11)得:
(13)
整理式(13)得到电机温度与电流的函数关系:
(14)
将式(14)化简得到:
T=K3I2+T1+T0
(15)
当时间一定时,电机温度为电流的幂函数。当电机预计达到的温度确定,即T为一定值时,由式(13)可得:
(16)
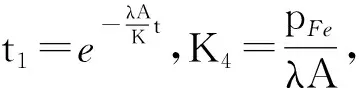
(17)

T-T0=(1-t1)(K4+K5I2)
(18)
将1-t1设为时间参数t2,将T-T0设为温度常数参数C,将I2设为电流参数I1,则式(18)可化简:
(19)
故当电机温度为定值时,时间参数t2与电流参数I1为反比例函数。
3 实验与参数整定
3.1 实验方法与数据处理
由于电机内部温度的直接测量不易实现,参考电机温度场相关文献[5-8]发现,电机运行中各点温升情况不同,选取电机外壳定子绕组的安装位置作为温度测量点,该测量点温升较快且便于测量.假设电机温度测量点的温度变化与整体电机成线性关系,则式(12)和式(15)以及式(19)适用于选取的测量点温升情况。为验证上述方法的正确性,同时考虑到实验的操作性与安全性,选取一款24W小功率电机进行实验,电机额定电压24V。在室温环境下进行实验,利用测温枪测量测试点温度并记录,将测量数据利用MATLAB中CurveFitting模块进行数据处理拟合电机温度特征曲线。多次实验后将所得曲线参数进行处理得到该电机特征曲线。部分实验数据如表3~表5所示。
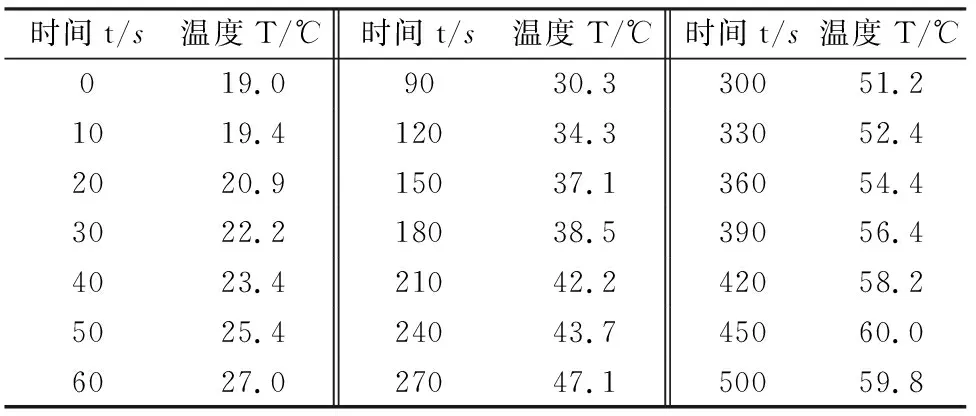
表3 电机温度变化Ⅰ
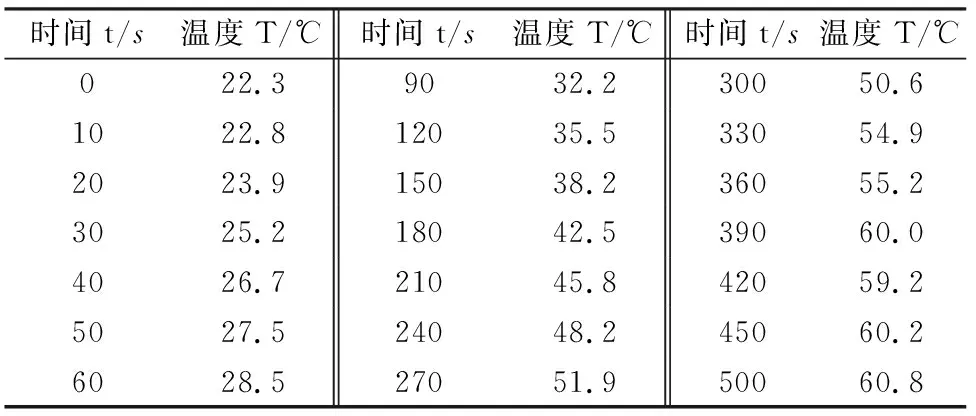
表4 电机温度变化Ⅱ
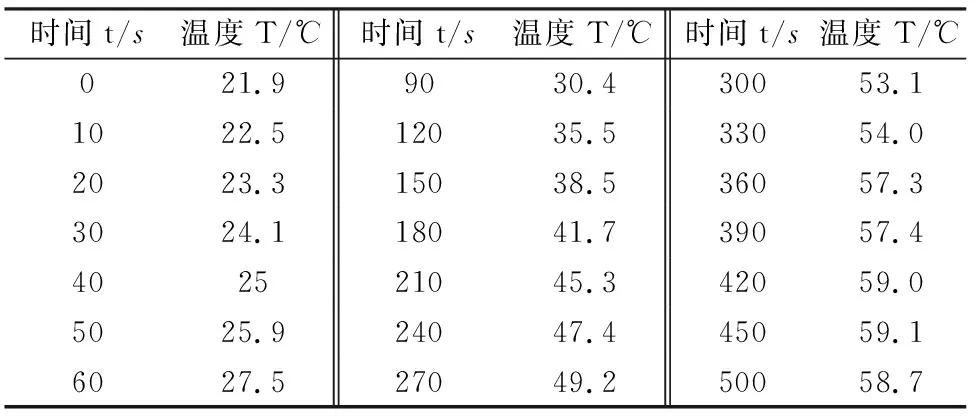
表5 电机温度变化Ⅲ
得到的部分电机温度特性曲线如图1所示。

(a) 表3温度变化及拟合曲线

(b) 表4温度变化及拟合曲线

(c) 表5温度变化及拟合曲线
图1电机温度特性
拟合的部分特性曲线参数如表6所示。

表6 部分温度特性曲线参数
由于T0包含电机初始温度即环境温度,假设环境温度为一定值,对参数T0进行处理得:
T1=T0-T2+T3
(20)
式中:T1为转换后的电机参数;T2为电机初始温度;T3为环境温度。将电机温度特性曲线参数进行最小二乘法计算处理,得到最终该电机温度特性曲线:
T=-41.32e-0.004 1 t+41.32+T3
(21)
改变电机附加扭矩,采用上述方法得到该电机不同负载即不同电流时的电机特性曲线,以电流0.6 A时为例,测得部分电机参考点温度如表7所示。

表7 电机参考点温度
其特征曲线如图2所示。

图2电机部分温度特性
得到电流0.6 A时电机特性曲线表达式:
T=-13.49e-0.004 1 t+40.02
(22)
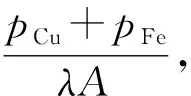
K1=K4+K5I2
(23)
将上述电流值与K1值代入式(23)可得K4,K5值,K4=1.71,K5=32.74。为验证上述计算的正确性,进行多次实验,测定不同电流时电机特性曲线。选取电机测量点温差为25℃,即温度常数C为25时,对电机温度参考点进行曲线拟合,部分电机温度参考点参数如表8所示。

表8 部分过载时间参数
得出结果与上述计算基本相同,基本检验了电机过载时间曲线的正确性。由于温度常数参数C为电机实际温度与环境温度的差值,则当电机到达任一温度时,该电机任一温度时的过载时间曲线:
(24)
同时,为进一步验证上述理论计算与实验的正确性。采用另一款功率为26 W无刷直流电动机进行实验,实验结果与上述实验基本相符。
3.2 实验结果误差分析
1)电流波动引起电机铜耗波动
电机加载运行过程中,电机母线电流存在一定程度的波动,这将引起电机铜耗热量,产生一定程度的波动。
2)电机温升引起的电机绕线电阻的变化
铜的电阻随温度升高而增加,会导致当电机温度升高时参数 会小幅度上升,电机实际值应略大于电机计算值,但铜的电阻值受温度影响变化较小,对电机温度曲线影响不大。
3)电机导热速率的影响
电机导热速率的影响是上述实验误差的最主要原因。由上述实验可以看出,电机拟合温度曲线与温度实际测量值相比,拟合温度曲线初始温度低于实际温度;当电机加载运行时间较长时,电机实际稳态温度高于拟合曲线温度。这是因为选取的电机温度测量点受电机导热速率影响,当电机加载运行初期,由于导热速率受限,测量点温度变化较为缓慢,导致曲线初始温度低于实际温度,当电机运行时间较长,基本达到稳态温度时,电机导热充分,测量点温度更加接近电机内部线圈温度,所以电机测量点实际稳态温度高于拟合曲线温度。
3.3 参数整定
基于上述误差原因分析,在电机的实际工作过程中,当电机高倍过载工作时电流较大,由于稳态温度较高,当电机工作在温度上升区间时即进入电机温度保护状态,在实际应用中电机温升曲线绘制应选择电机温升区间并去除初始短时间内参考温度进行曲线拟合,得到电机温升公式,利用最小二乘法对电机温升参数进行参数整定,得到与电机实际工况下最为接近的温升曲线。
4 结 语
1) 针对某履带全方位无人平台的特殊需求,提出了一种基于特定电机过载时间曲线的电机控制方法。通过理论分析得出了特定电机负载恒定时电机温度与时间、电机预期温度恒定时电机负载与时间之间的函数关系,通过多次实验得出了电机温度特性曲线与过载时间曲线,并对实验结果进行了误差分析,实验结果与理论分析基本相符,基本验证了该电机控制方法的正确性。
2) 利用上述方法得出电机负载时间曲线可以最大程度地提高电机的过载能力,对于减小该地面平台质量,提升其越野加速性能有重要意义。
3) 本文提出了一种全新的电机过载控制方案,该控制方案不仅可以满足该履带平台,同时可以推广到各种运动环境较为复杂的地面平台。该方法可以改善电机外特性曲线,扩宽电机的负载范围,具有较高的应用前景与研究价值。

