具有Holling III类功能性反应的非自治扩散系统的持久生存

梁桂珍 ，赵 晓 ,2

（1.新乡学院 数学与信息科学学院，河南 新乡453003；2.郑州大学 数学与统计学院，河南 郑州450001）

随着全球性的环境污染及生态环境破坏程度的加剧，种群会从一块栖息地迁移到另一块栖息地。另外，环境随季节呈现出的周期性变化也会导致种群的迁栖。因此，在考虑种群的密度制约因素以及交互作用过程、捕食者对食饵的功能性反应等情况时，考虑时变环境特别是周期环境下的扩散系统才更贴近现实。1974年，S.A.Levin［1］首先建立了斑块环境下的种群动力学系统，随后其他学者考虑了扩散对种群持续生存的影响［2-5］。 1965 年，C.S.Holling［6］针对不同类型的物种提出了3种不同的功能性反应函数。后来，不少学者对带有Holling型功能反应函数的种群系统模型做了进一步的研究分析，得到了一些有价值的成果［7–8］。罗红英等［9］研究了一类带有HollingⅡ型功能反应函数的非自治捕食扩散系统的周期解及其渐近稳定性。HollingⅡ类功能反应函数由于是线性的，只适用于无脊椎动物，具有一定的局限性。为了准确描述实际的生态捕食系统，我们将在文献［9］的基础上研究如下带有HollingⅢ类功能性反应函数的非自治扩散捕食系统：

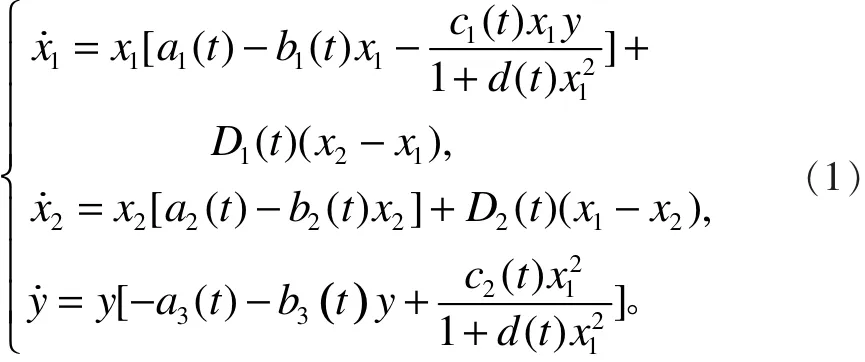
1 基本引理

引理 2：若 ( x1( t), x2(t),y(t ))是系统（1）满足初始条件的任一正解，则在满足条件（2）的前提下有以下结论成立：

1）存在正数 T1，使得 t ≥ T1时有

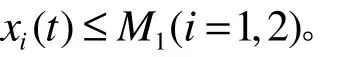
在以上式子中，有

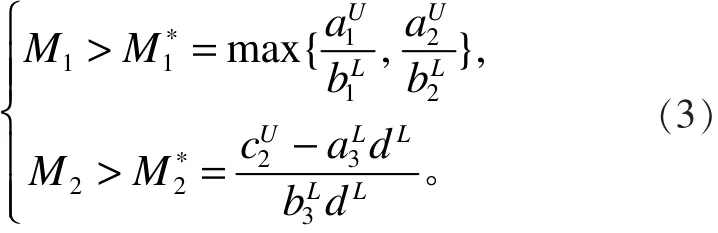
证明：先证结论1）。由系统的前两个方程可得

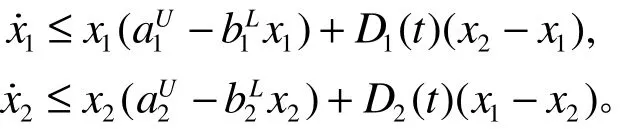
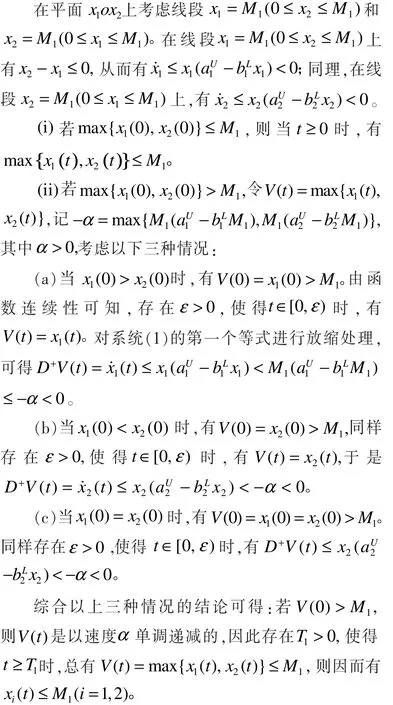
再证结论2）。由系统的第三个方程可得

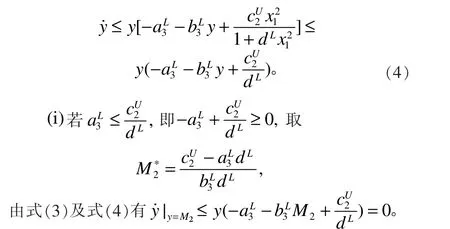
考虑以下两种情况：

（a）若 y (0) ≤ M2,则当 t ≥0时，有y(t)≤M2。

（b） 若 y ( 0) > M2,则 存 在 T2> 0 ,当 t ≥ T2时 ， 有y(t) ≤M2。

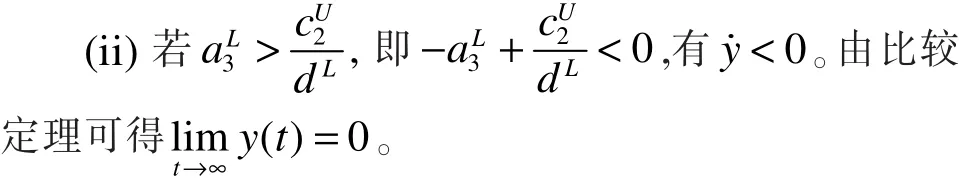
推论1：定义S ≜ {(x1, x2, y) |0 < xi≤ M1, 0 < y≤M2,i=1,2},则在条件（2）成立的前提下,当时，S是系统（1）的正向不变集和最终有界集。

2 一致持久生存

定理 1：若系统（1）满足假设（2），条件

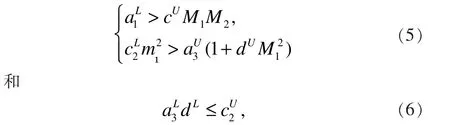
则系统（1）是一致持久生存的。

证明：由推论 1 可知，当系统（1）满足条件（6）时，S 是系统（1）的正向不变集和最终有界集。不失一般性，假设系统（1）具有正初始值的任一解(x1( t) ,x2(t) ,y(t) ) ∈ S,其中 t ≥0。取

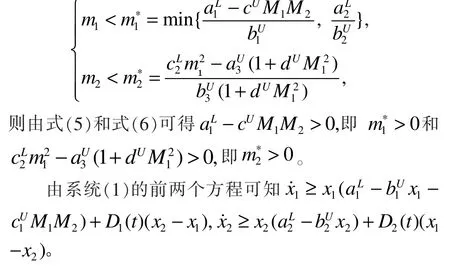
令V(t) = min{ x1( t), x2(t) } ,0 < m10,当 t ≥T3时，有 V (t) ≥m1。 因此，对于充分大的t，有xi(t) ≥ m1(i =1,2)。

又由系统（1）的第三个方程可知

3 周期解的存在性与全局渐近稳定性

假设系统（1）中的所有参数都是 [ 0,+ ∞)上周期为ω的连续函数，则称该系统是 ω -周期的系统。

则有 A (S1) ⊂S1。又由解对初值的连续依赖性可知映射A是连续的，且S1显然为闭的有界凸集，故由定理2可知，A在S1中必有 z*满足 A (z*) =z*，因而系统（1）存在一个周期为 ω 的正解。

下面考虑系统（1）的周期解的唯一性及全局渐近稳定性。

定理 4：周期系统（1）在满足假设（2）、式（5）、式（6）及下列条件

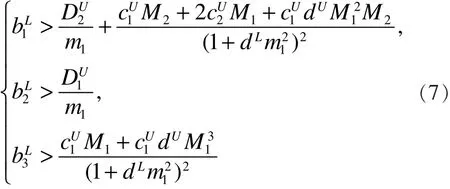
的前提下存在唯一的全局渐近稳定的周期解。

证明：由定理 3可知，系统（1）在满足假设（2）和式（5）、式（6）的前提下，至少存在一个严格正的周期解U(t) ={v1( t),v2(t),w(t)}。

设X(t) ={x1( t), x2(t),y(t )}是系统（1）具有正初始值的任一解，则由定理1可知系统（1）具有正初始值的任意解都将最终进入 S1。因此，存在 T > 0 ，当 t ≥ T时，有 U (t) 和 X (t)∈S1。设 f (t)为 [ 0,+∞)上的连续可微函数，则有

构造Liapunov函数

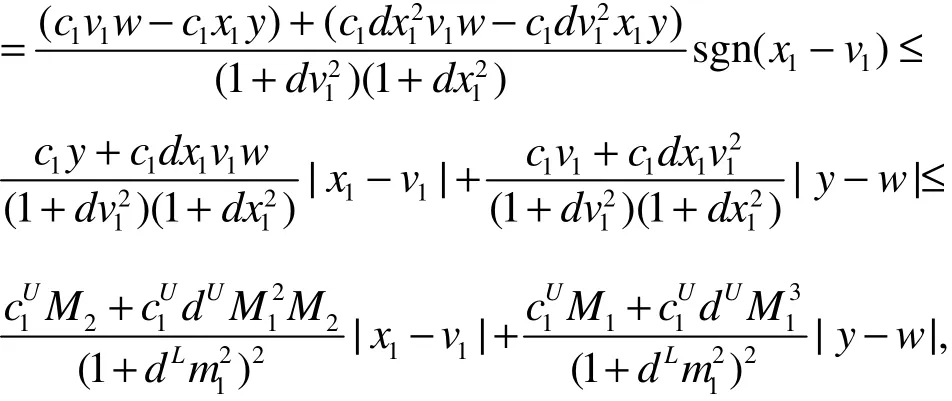
于是有

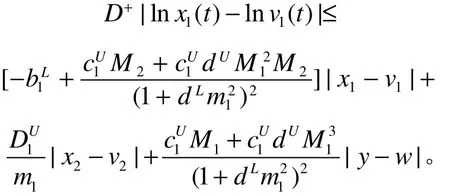
同理可得

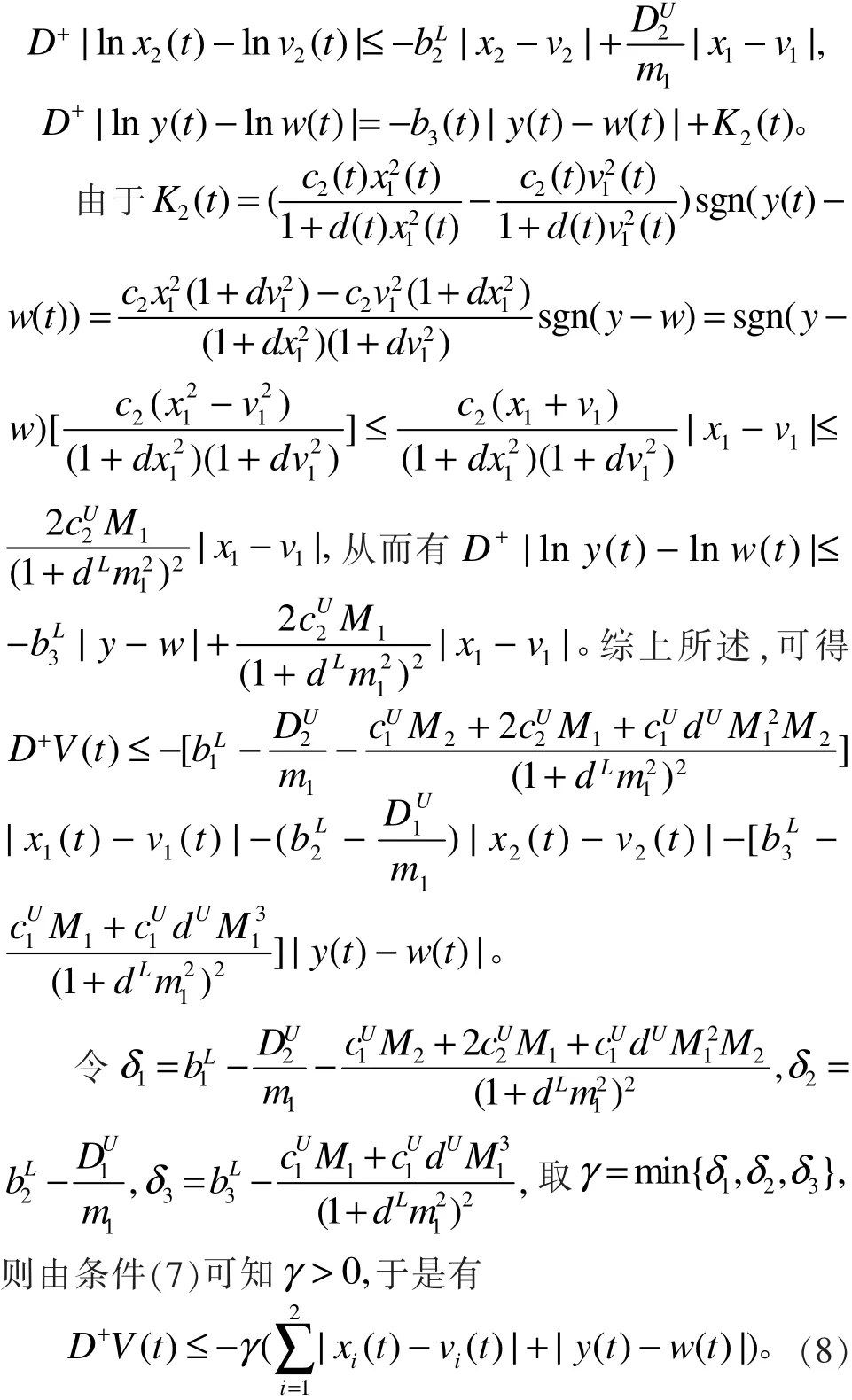
由式（8）可知在Liapunov意义下系统是稳定的。

对式（8）两端求从0到t的积分，有

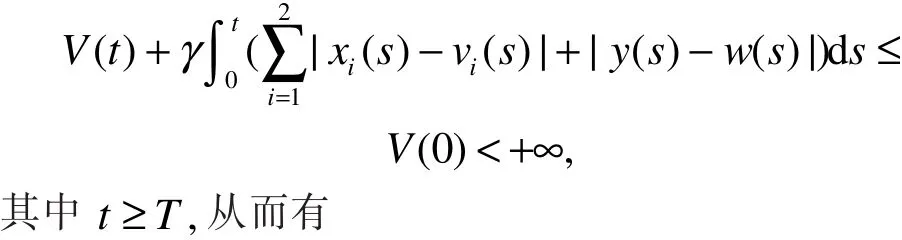
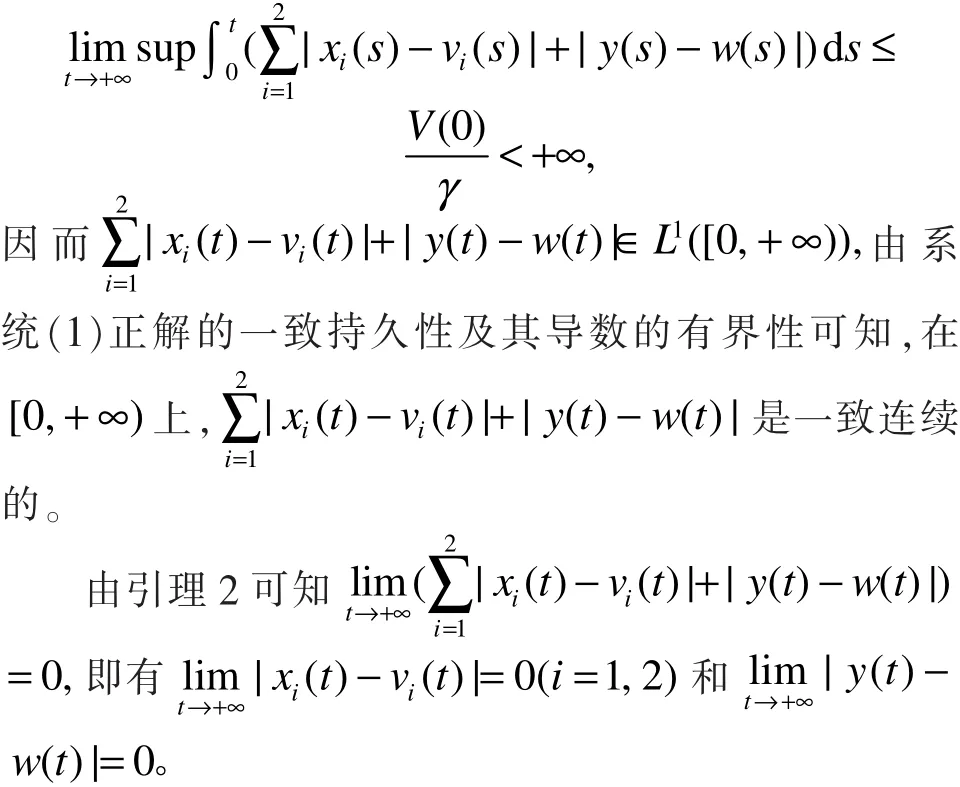
由定义2可知系统（1）存在唯一全局渐近稳定的周期解。

4 数值模拟

为了验证定理1结论，我们如下建立系统

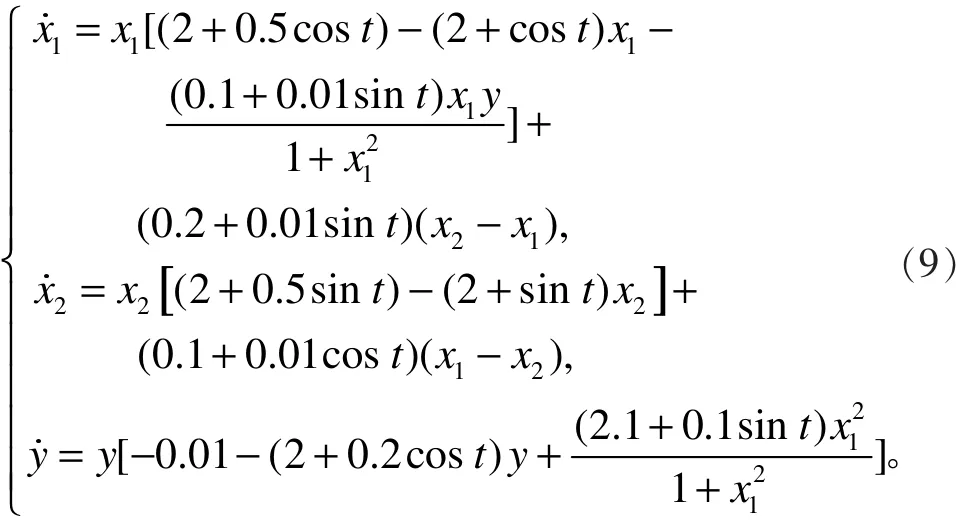
显然，该系统以 2 为周期，并满足定理1的所有条件。取m1= 0.37, m2= 0.01, M1= 2.6,M2=1.3,则有

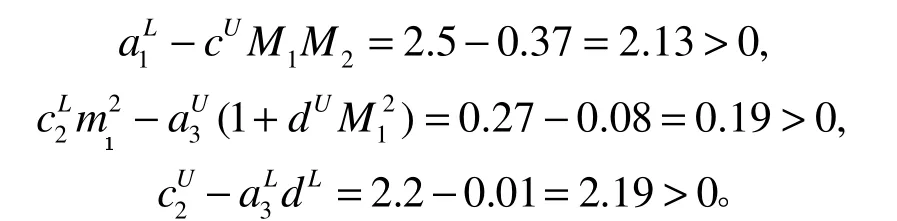
取初始条件 x1(0) = 2 , x2(0) = 2 ,y (0)=1，运用Matlab软件进行数值模拟，结果见图1。

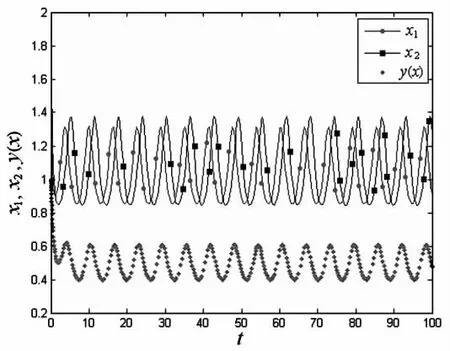
图1 系统（9）的数值模拟结果

5 结束语

在本文中，我们研究了一类非自治捕食扩散系统，得出了以下结论：当系统（1）满足定理1的条件时，该系统会一致持久生存下去，且该系统的持久性与扩散系数时,捕食者种群将趋向灭绝；定理4的结论表明该系统的全局渐近稳定性与扩散系数D1和D2密切相关。该结论对实际生产、生活有一定的启示，为有关部门的决策提供了有价值的参考。