基于RSSR机构的无碳小车运动分析及优化

陈 雷, 刘同义, 许同乐

(1.中北大学 仪器与电子学院 山西 太原 325000;2.山东理工大学 机械工程学院,山东 淄博 255049)

基于RSSR机构的无碳小车运动分析及优化

陈 雷1,2, 刘同义2, 许同乐2

(1.中北大学 仪器与电子学院 山西 太原 325000;2.山东理工大学 机械工程学院,山东 淄博 255049)

为解决基于空间RSSR机构“8”字形轨迹无碳小车在运行中稳定性不高的问题，采用当量平面机构法分析空间RSSR机构，对其驱动机构进行运动分析，并运用微元法计算车轮的运行方程从而建立完全参数化的系统模型.运用MATLAB的计算功能对系统运动进行仿真，得到了整体的优化方法，从而优化了小车的运动轨迹.

无碳小车；“8”字形轨迹；空间RSSR结构；转角

“8”字形轨迹无碳小车是全国大学生工程训练综合能力竞赛项目，要求小车必须具有自动控制转向机构,且此机构应具有可调节功能,经过调试小车能自动行驶出闭合轨迹.该小车轨迹平滑度和运行稳定性是由转向机构决定的，当前参赛队伍设计的转向机构大都采用间歇性机构[1-2],如不完全齿轮、槽轮等,此类结构的小车在运行中平稳性不高.要解决这一问题，可采用连续性机构(如连杆机构)作为转向机构.空间四杆机构不但结构紧凑，而且灵活可靠，因此空间四杆机构在无碳小车转向设计中将具有更高的可调性.本文以空间RSSR机构为原型设计“8”字形轨迹无碳小车的转向机构，对无碳小车各机构进行运动学分析，创建完全参数化的系统模型并对其优化，以期得到理想的运行轨迹.

1 驱动原理及其优化

1.1 驱动原理分析

基于RSSR机构的无碳小车整体结构如图1所示，自上而下，T为定滑轮固定在车架顶端，绳l绕过定滑轮T悬挂砝码F，于是砝码的重力经绳l传递到了位于车架低端的主动轮1(半径为r1)上，即在绕线轴上产生驱动力矩M=Gr1.主动轮1的转矩经一级齿轮传动传递到后轮H1/H2(一级齿轮的传动比为i23)，组成定轴轮系1-2-3-H1/H2，同时主动轮与空间RSSR机构的曲柄L1联接，曲柄L1、连杆L2和摇杆L3通过两个球铰链连接成空间曲柄摇杆机构，即空间RSSR机构[3]，小车正是通过该机构控制前轮的转向.

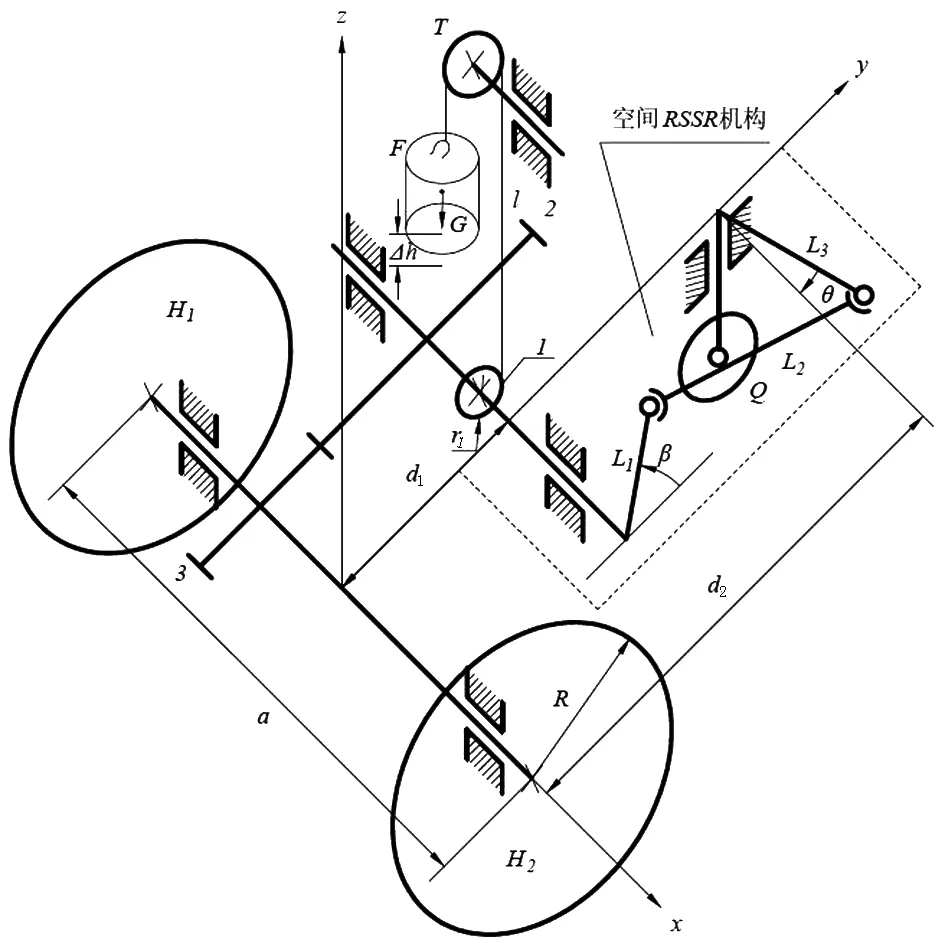
图1 小车整体结构图Fig.1 Overall structure of the vehicle

如图1所示，β、θ分别为空间RSSR机构的输入角和输出角.由于绳l为轻质刚性绳，砝码下落的速度等于主动轮1外圆上任意点的线速度，当砝码下落一定高度h时，有

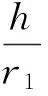
(1)

设后轮转过的路程为s，在定轴轮系1-2-3-H1/H2中有

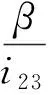
(2)

将(1)式代入(2)式得

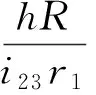
(3)

1.2 驱动系统的优化

以往采用单轮驱动方案实现左右轮的差速运动.单轮驱动是将一后轮直接与从动轮3联接，驱动力矩经一级齿轮传动传递到该后轮，该后轮始终作为驱动轮驱动小车运动.另一后轮采用深沟球轴承作为差速器支撑从动轮3，以实现差速运动.由于在单轮驱动方案下，小车运行在左、右两半周期时所需的驱动力矩不同，将导致小车两半周期的运行速度出现一定的波动，不利于小车的平稳运行.

本文采用双轮驱动方案对小车驱动系统进行优化，双轮驱动原理如图2所示.两后轮都采用单向滚针轴承作为超越离合器，同时支撑从动轮3.超越离合器可以实现后轮的转速超越从动轮3的转速，而从动轮3的转速不可以超越后轮的转速.当小车运行时，外侧轮的转速总是大于内侧轮的转速，因此外侧轮的转速将超越从动轮3的转速.而内侧轮的转速等于从动轮3的转速，从动轮3带动内侧轮驱动小车运行.在一个周期内，小车分别以左右轮为内侧轮的运行阶段各为半个周期，因此小车运行时左右轮将交替作为驱动轮驱动小车运行，进一步提高了小车运行的稳定性.

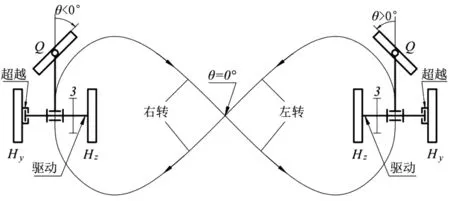
图2 双轮驱动原理图Fig.2 Two-wheel drive principle

2 转向机构分析

如图3所示空间RSSR机构中，在A、B、C和D处的运动副依次为转动副R、球面副S、球面副S和转动副R.该无碳小车采用的RSSR机构是一种主、从动轴垂直交错(叉角等于90°)的正置式空间连杆机构[4].主动轴装配在绕线轴上，由重物牵引绳牵引驱动，从动轴装配在前轮转向轴上直接控制前轮的转向.

2.1 空间RSSR机构的运动分析

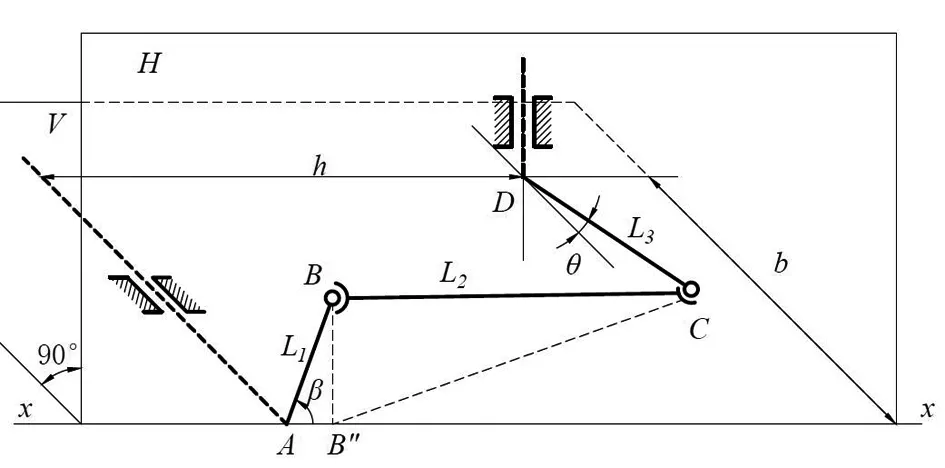
图3 空间RSSR机构Fig.3 The spatial RSSR mechanism

采用当量平面机构法对空间RSSR机构进行运动分析.如图3所示，主动杆AB和从动杆CD分别与机架组成转动副，且主动轴A在从动杆CD的摆动平面内，而连杆BC分别与主动杆AB和从动杆CD组成球面副.通过B和C各做平面H和V分别垂直于主动轴A和从动轴B，两平面的交线为xx.B点在平面V上的投影为B″，它一定在直线xx上.当主动杆AB绕轴A回转，即点B作以A为圆心、L1为半径的圆周运动时，其投影B″沿xx作直线往复运动.从而，在平面V内可构造摇杆滑块机构DCB″，其中从动杆DC具有实长L3，而连杆B″C的长度l2是变化的，空间RSSR机构的当量平面机构如图4所示.又在平面H内构造正弦机构，正弦机构的导杆运动与点B″的运动相同[5].在该正弦机构中有

g=h-L1cosβ

(4)

在V平面内的摇杆滑块机构中，连杆B″C的可变长度l2由图4所示的直角三角形BB″C求得，即

(5)

以BB″=L1sinβ(见图4)代入(5)式得

(6)

在图3所示的V平面内建立右手坐标系xDy，按多边形各边的几何关系，有

(7)

消去α并整理，得

hcosθ+dsinθ+J=0

(8)

解得

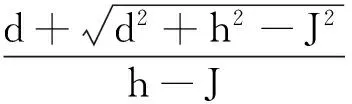
(9)

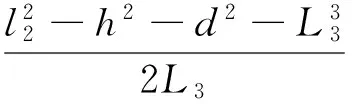
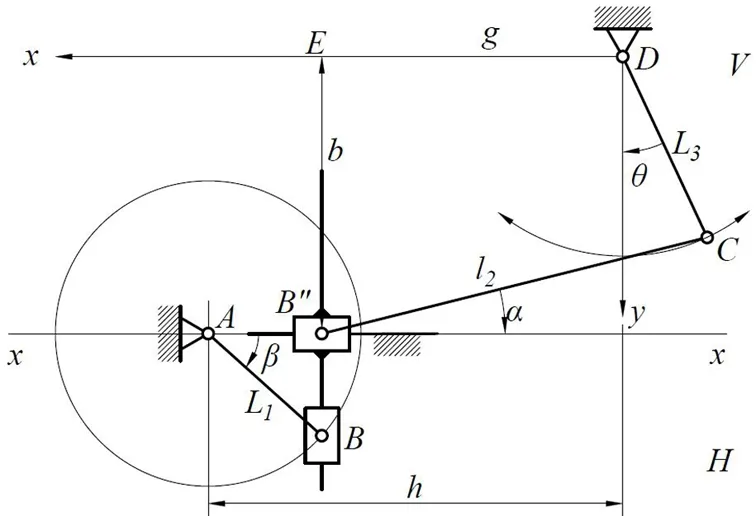
图4 当量平面机构Fig.4 The equivalent plant mechanism

2.2 空间RSSR机构的传输特性

空间RSSR机构的自由度为1，将主动轴的回转角定义为输入角，从动轴的摆动角定义为输出角.按上述的运动分析，得到正置式空间RSSR机构的传输特性θ=θ(β)，对θ(β)求一阶导数得到θ′(β)，求二阶导数得到θ″(β)，它们分别对应L3的角位移、角速度和角加速度.如给定：L1=28.7mm,L2=74.1mm,L3=38mm,h=74mm，b=40mm，则其传输特性曲线如图5所示.由图5可知，一个周期内的θ(β)曲线关于直线β=π对称，正置式空间RSSR机构无急回特性；θ′(β)曲线和θ″(β)曲线变化平稳、无突变，该机构在运行过程中并无冲击和跃度，在高速运行下也不会产生振动，因此采用空间RSSR机构有利于小车的平稳运行.RSSR机构的传输特性将直接决定了小车的运行轨迹，合理的选配其各构件的尺寸可以优化运行轨迹.

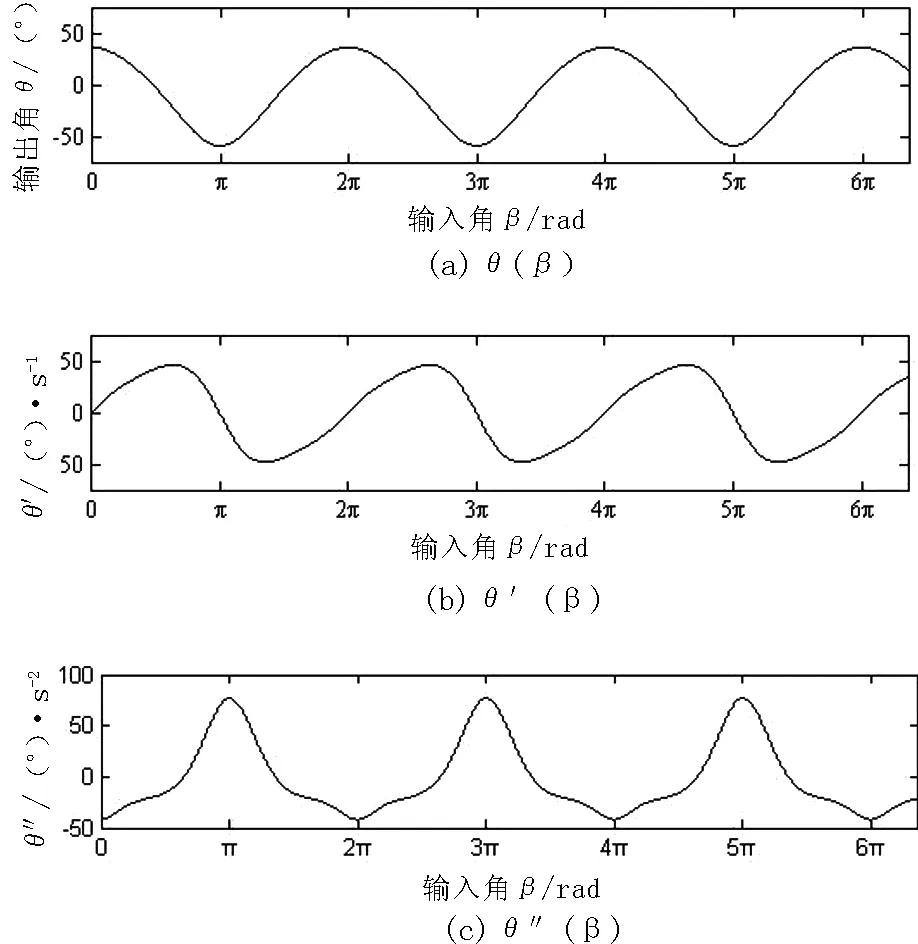
图5 空间RSSR机构的传输特性Fig.5 Transfer characteristic of spatial RSSR mechanism

3 小车轮迹求解

方便起见，以右轮为例分析其运行轨迹.如图6建立坐标系xOy，在一个轨迹周期内，若小车以左轮(内侧轮)为驱动轮运行在右半周期(即θ>0°)的某一位置，砝码下落的高度为h，由式(1)知曲柄的回转角为β=h/r1，车体相对地面转过的角为φ，由空间RSSR机构的传输特性可得前轮转角θ.

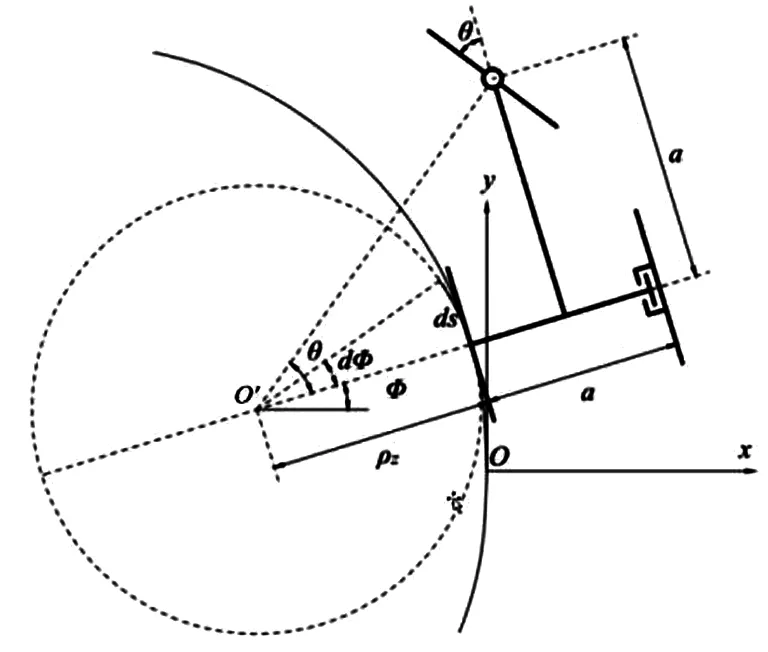
图6 微元法轨迹解析Fig.6 Trajectory analysis by infinitesimal method

3.1 车轮运动学分析

采用微元法对小车进行运动学分析，在砝码下落极小的高度dh内，由式(3)得左轮(内侧轮)绝对位移为

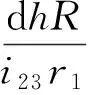
(10)

由图6中的几何关系得轨迹半径[6]为

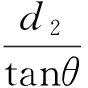
(11)

图6中点O′即为曲率中心，同时也为瞬心，故右轮(外侧轮)绝对位移为

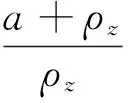
(12)

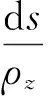
(13)

式中,θ=θ(h).

3.2 车轮的运动方程

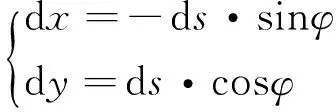
(14)

式中，φ=φ(h).

当小车运行在左半周期时，左轮转变为外侧轮，其绝对位移ds=ds'，同理可得小车运行在左半周期时左轮的运动方程为

(15)

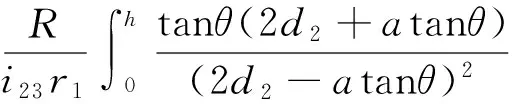
由几何关系可得右轮的运动方程为

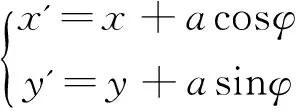
(16)

前轮的运动方程为

(17)

4 运动仿真

根据小车各机构的参数化模型，在MATLAB软件中编程模拟小车系统，给各参数赋初值，便可得到小车运行的仿真轨迹[7].但还需要对各初始值进行调整，才能使模拟系统仿真出“8”字形轨迹.驱动系统中的参数(d1、d2、a、R、r1、i23)可以通过外形尺寸的设计首先确定下来，转向系统中的参数(L1、L2、L3、b、h)需要多次调整才能使小车的模拟路径趋于闭合,其调整过程如图7所示.由此可知，若要实现无碳小车按“8”字形轨迹运行，要求前轮的摆动角Δθ=θmax-θmin≥82.5°.图8给出的是构件L2=75mm，h=70mm时Δθ-k-L1曲线变化情况.其中k=L1/L3，用来为满足前轮摆动角Δθ≥82.5°的要求，调节各构件尺寸时提供参考.

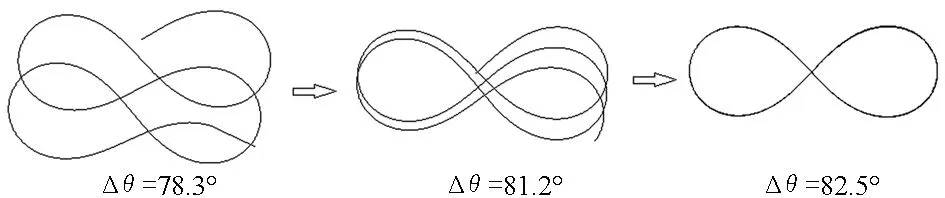
图7 仿真调试过程Fig.7 The process of debugging simulation

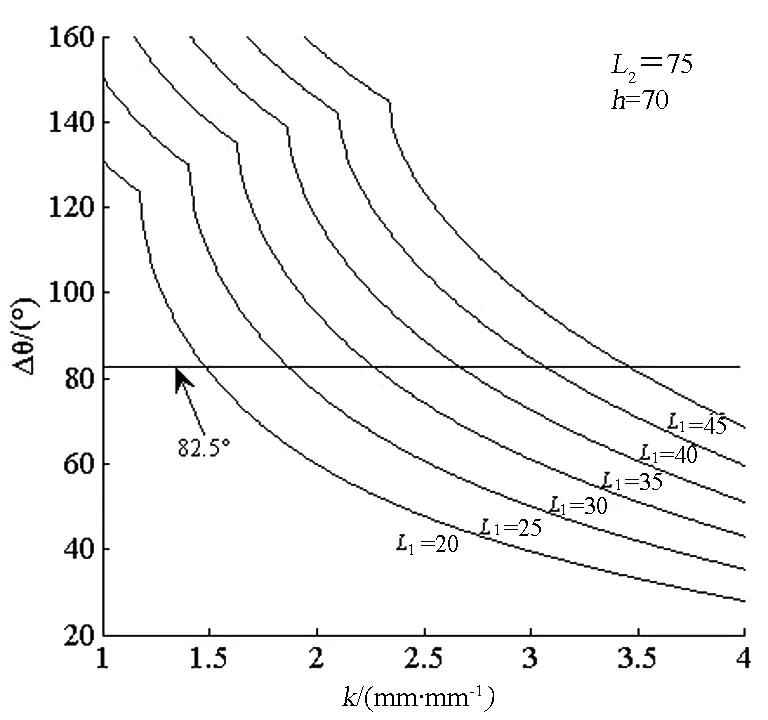
图8 Δθ-k-L1曲线Fig.8 Δθ-k-L1 curvecurve

采用单轮驱动时各机构尺寸具体的赋值参数与仿真轨迹如表1和图9所示; 采用双轮驱动并对各参数值优化的结果如表2和图10所示.

表1 无碳小车赋值参数
Tab. 1 Assigned parameters of the carbon-free vehicle

绳后轮轴距d1/mm前后轮轴距d2/mm两后轮间距a/mm后轮半径R/mm绳轮半径r1/mm传动比r12曲柄L1/mm连杆L2/mm摇杆L3/mm绳前轮轴距h/mm曲柄面距b/mm40110808040.3332774376030

表2 无碳小车优化参数
Tab. 2 Optimization parameters of the carbon-free vehicle

绳后轮轴距d1/mm前后轮轴距d2/mm两后轮间距a/mm后轮半径R/mm绳轮半径r1/mm传动比r12曲柄L1/mm连杆L2/mm摇杆L3/mm绳前轮轴距h/mm曲柄面距b/mm43113907520.26528.774.1387040

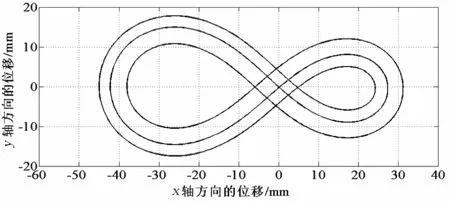
图9 仿真轨迹1Fig.9 The simulation trajectory 1

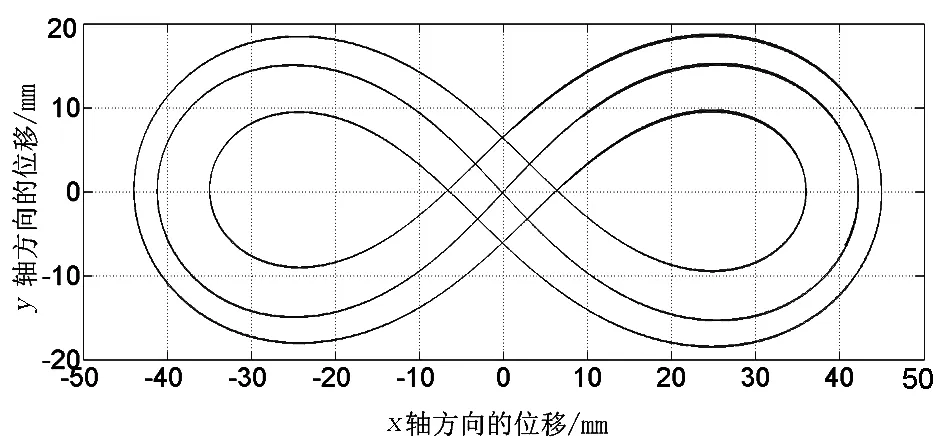
图10 仿真轨迹2Fig.10 The simulation trajectory 2

从轨迹图9和图10中看出，曲线光滑、连续，无跳跃， 即表明小车可以平稳运行. 由于加工制作中存在一定的误差，所以多个周期后小车会逐渐偏离原始的路径，其右侧轨迹直径较小造成小车右侧容易撞杆，大大影响运行的圈数.

[1]张宝庆，肖富阳，黎晓琳，等. 重力势能小车“轨迹法”创新结构优化设计[J].机械传动, 2012，32(3):32-34.

[2]张春，郑应彬，马永昌. 三轮重力势能小车大角度转弯性能优化[J]. 机械设计, 2014，31(10):50-55.

[3]周勇, 孙海刚. 某型空间RSSR机构图解分析与设计[J]. 北京理工大学学报, 2011,31(4):394-397.

[4]苗鸿宾，乔峰丽.空间RSSR机构运动分析的研究[J]. 机械设计与制造， 2008(2):7-9.

[5]林光春,高山，徐礼钜，等. 杆长和惯性参数可变的平面可调5杆机构的动力学解析模型[J]. 四川大学学报(工程科学版), 2005, 37(5):139-143.

[6]王政，何国旗，胡增. 基于ADAMS软件的无碳小车转向机构设计[J]. 湖南工业大学学报，2013，27(5)：28-32.

[7]王琦, 徐式蕴, 赵睿涛, 等. MATLAB基础与应用实例集粹[M]. 北京: 人民邮电出版社，2007.

Motionanalysisandoptimizationofthecarbon-freecarbasedonRSSRmechanism

CHEN Lei1,2, LIU Tong-yi2, XU Tong-le2

( 1. School of Instrument and Electronics,North University of China, Taiyuan 325000, China;2.School of Mechanical Engineering, Shandong University of Technology, Zibo 255049, China)

For this problem that the “8” shaped trajectory carbon-free vehicle which based on spatial RSSR mechanism is unstable in the operation, this paper applies the theory of equivalent plant mechanism to analyze the spatial RSSR mechanism, does a kinematics analysis of its driving mechanism and uses the micro-element method to compute the operating equation of its wheels in order to establish a fully parameterized model. By using MATLAB computing functions to do kinematics simulation analysis of the system, this paper gets an overall optimization methods, optimizing the car's trajectory.

carbon-free vehicle;“8”- shaped trajectory;spatial RSSR mechanism;corner

2017-01-05

陈雷，男，2545506372@qq.com；

刘同义，男，lty-0611@163.com

1672-6197(2018)01-0051-05

TP235

A

(编辑：郝秀清)