基于关联维计算的软件失效混沌识别研究

钱 丽，胡 俊，王美荣，沈桂芳, 陈 平

(安徽新华学院 信息工程学院,安徽 合肥 230088)

基于关联维计算的软件失效混沌识别研究

钱 丽，胡 俊，王美荣，沈桂芳, 陈 平

(安徽新华学院 信息工程学院,安徽 合肥 230088)

针对大数据环境下软件失效行为的复杂性问题，提出了一种基于关联维数的软件失效混沌识别算法.通过计算软件失效数据是否具有关联维特征来验证失效的混沌性，利用相空间方法重构软件失效系统，验证了软件失效行为的混沌性.实验结果表明，混沌关联维算法能够有效识别软件失效的混沌性，精确地描述软件失效行为的无序性和无规则性，同时也能解决复杂软件系统失效、大数据混沌性这类复杂问题.

大数据；软件失效；关联维；混沌识别

随着互联网、云计算技术的不断创新与发展，数据呈现爆炸式的增长，软件系统也变得日益复杂.软件安全性问题一直以来都是企业在运营过程中关注的焦点问题，复杂软件系统给企业的软件安全提出了更高的要求[1-2].目前比较常用的研究方法是通过对软件失效行为的分析，挖掘出复杂软件系统内在的本质演化规律[3].国内研究中，YANG等[4]采用叠加NHPP模型极大似然估计法来研究软件失效行为；程跃华等[5-6]采用主成分分析法研究软件失效机理，解决软件可靠性度量存在的多重共线性问题；台湾LIN等[7]提出性能模型演示的实验方法进行软件失效分析；楼俊钢等[8]采用主成分回归算法和支持向量回归等核函数回归估计方法研究软件失效行为.国外研究中，INOUE等[9]提出离散型软件可靠性模型，不同于连续时间上的软件可靠性模型，较好解释软件失效行为；LANDONA等[10]开发贝叶斯推理模型和强化泊松过程模型，并且实施于实际软件故障数据预测模型的过程；ZHENG等[11-12]研究者提出基于神经网络的非参数式建模方法研究软件失效行为，这种方法不同与以往基于一些主观假设条件的SRGM，对软件可靠性的度量、预测的精度有很大的提高，但对软件失效行为的本质分析不够透彻.

以上研究主要基于概率论与数理统计方法，假定软件失效行为符合某种概率分布，使用可靠性随机模型来分析软件失效过程，这种研究观点与方法具有一定的主观性，较难解决软件失效、复杂软件系统失效行为的混沌性问题.大数据环境下的软件失效行为不仅具有随机性，也具有确定性，软件失效行为的本质与混沌特性是具有相似性的，虽然受到确定规则的约束，但是其行为却表现出无序性.因此，本研究将混沌关联维特征计算应用到软件失效行为的分析上，比随机模型更好地描述软件失效行为的无序性和无规则性，同时也能够解决软件失效、大数据混沌性这类复杂的问题.

1 混沌识别特征量分析

复杂软件系统失效行为的演化过程中，可以将测试人员、软件和运行环境看做一个复杂混沌系统，系统中各个分量之间相互影响作用，复杂软件系统不断地向前演化，在此过程中应用混沌时间序列分析软件失效行为的演化规律.软件失效的混沌现象是指系统在确定系统中貌似随机的不规则运动，其行为表现出不可预测，无序的状态.软件失效行为的混沌特征通常表现为无明显规则和次序、非同期性的复杂折叠和扭曲，软件失效行为的混沌识别通过计算Lyapunov指数和关联维数等混沌特征量来判断软件失效数据是否具有混沌性.

1.1 Lyapunov指数

在对软件失效行为的分析过程中，所收集的失效数据只是整个软件失效系统的局部观测值，如果要研究系统的演化规律，就要计算嵌入维、时间延迟，重构与原空间微分同胚的相空间.相空间是一个六维假想空间，其中动量和空间各占三维.物理学中的相空间由系统的状态点组成，相空间的维数由质点系的“自由度”个数来决定.若用x来表示质点所在的位置，那么质点速度由x对时间t的一阶导数xdx/dt表示，(x，y)表示系统的一个状态点，所有状态点的集合就构成了系统的相空间.通过重构相空间可以挖掘系统的演化规律.

混沌系统的运动轨道具有初值非常敏感性，相空间中初始距离靠近的两条轨迹以指数速率发散，通过Lyapunov指数形式描述.初始两点在一维动力系统xn+1=F(xn)中迭代后，它们的分合程度取决于|dF/dx|的值：大于1则两点分离；反之则靠拢.假设初始点x(t0)附近有一点x(t0)+Δx(t0)，则经过n次迭代后，

x(tn+1)+Δx(tn+1)=f[x(tn)+Δx(tn)]≈

f[x(tn)]+Δx(tn)f′[x(tn)]

因此，

Δx(tn+1)=Δx(tn)f′[x(tn)]

(1)

其中，t0和tn分别为初始时间和当前时间.假设相空间两点轨迹的初始距离为|Δx(t0)|，经过n次迭代后两点的距离为|Δx(tn)|，由上面式(1)得出：

|Δx(t0)|exp(λtn)

系统的Lyapunov指数, 当λ<0时，则系统是稳定的；λ=0时，则系统是周期的；λ>0时，则系统是混沌的.

1.2 关联维数与嵌入维数

大数据环境下的软件系统是确定的，系统的变化状态由若干变量决定，其中变量的个数即为系统的维数.混沌系统虽然在高维空间上表现无序、无规则，但是由于相空间的收缩，系统中的自由活动将越来越少，而相空间联系和整体约束越来越强，最终趋向于低维空间的极限，也就是所谓的奇异吸引子.如果奇异吸引子存在于软件失效的观测时间序列{x(t)}中，关联指数D随着嵌入维数m的增大而增加，直至观测到关联指数D收敛为一饱和值时，那么可以用关联维数描述此吸引子的特征.关联维通常采用关联积分计算观测变量前后的相互关联性，从而描述信号的确定程度和规律.

本研究借助G-P算法计算大数据环境下的软件失效数据的关联维数，其算法主要思想是选择不同的领域半径r，分别计算相应的C(r)，从而得到D.当求得数据的饱和值后，根据失效数据的嵌入维数(m≥2d+1)，即可确定维数m.复杂软件环境下混沌系统在高维空间是无序的，但当其投射到低维空间时，就会得到规律性的轨迹，在这个过程中，系统的轨迹也会产生变化.混沌运动表现出的特征在很多方面，例如，某些点虽然在高维空间中相邻，但是投射到低维空间后却不相邻；而某些在高维空间不相邻的点投射到低维空间时却相邻，这也是混沌运动表现出的特征.在重构系统相空间的时候，通常去除这些伪邻居点，根据复杂环境下混沌系统的这种几何原理来计算嵌入维，其计算步骤如下：假设{Xn}为混沌时间序列，τ为时间延迟参数，针对某个维数d，可以重构向量序列{yi(d)}，

yi(d)表示d维重构所得到的第i个向量.这里定义：

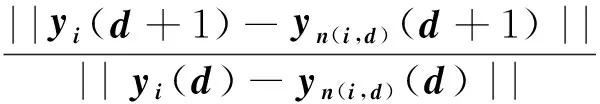
其中i= 1，2，…，N-dτ，||…||为无穷范数.n(i,d)为大于等于1且小于N-d的整数.：yn(i,d)(d)为离yi(d+1)最近的向量.a(i,d)均值定义为).

为了解E(d)的变化，定义：

E1(d)=E(d+1)/E(d)

若吸引子被包含在时间序列中，当维数d大于某个初始值d0时，E1(d)就会停止变化.那么最小嵌入维数为d0+1.

在实际复杂环境中得不到系统的所有分量，所以只有将系统投影到平面或直线上观测，进而采集系统局部的一个到两个分量的时间序列，空间维数的估算可以通过嵌入维靠近关联维数算出.软件失效的混沌识别，在于关联维数随着嵌入维数的增大最终是否收敛，如果收敛于一个稳定值则系统是混沌的；如果不收敛，则是随机的.软件可靠性建模通常先收集软件的失效数据来进行混沌识别，然后通过计算特征量来验证失效行为的混沌性.

2 软件失效行为的混沌识别

大数据环境下的复杂软件系统需要满足数据量大，数据类型多、运算速度高的特点，并且软件系统本身具有复杂性和不透明性等特点，使得软件失效行为变得不确定和难以预测.在实际软件系统运行过程中，软件失效的无序性、无规则性，不仅仅具有随机的特点，更具有混沌的性质，正如现实中大多数系为也是如此.复杂环境下软件失效行为的混沌性识别过程中，首先收集失效数据，然后验证失效数据的混沌性，进而分析与预测软件失效行为.

软件失效行为的分析和预测的前提是对软件失效数据的验证，通过验证软件失效数据来分析软件失效行为的混沌性.失效数据的收集一般在软件实际运行中进行，分为完全数据和不完全数据两种类型：

(1)数据集合{y(i) |y(0) =0，i= 1, 2, …, n }为完全数据集合，如果：∀：i(i∈{1, 2, …,n}→y(i)-y(i-1) = 1)，其中y(i)为直到时间t(i)时的累积故障数.

(2)数据集合{y(i) |y(0) =0，i= 1, 2, …,p}为不完全数据集合，如果：∃i(i∈{1,2,…，p}→y(i)-y(i-1)> 1).

复杂环境下软件失效行为虽然表现为无序、随机，但其本质上是具有一定的确定性的，通过计算混沌特征量来判断软件失效行为是否具有混沌性，并且借助G-P算法计算关联维和嵌入维数，进而验证失效行为的确定性，具体计算过程如下：

(1)对于时间序列x1,x2,…,xn, 假设其中m0为一个较小值，则重构相应的相空间为Yi=(xi,xi+τ,…,xi+(m-1) τ), i = 1, 2, 3,…,M.

(2)计算关联函数

其中θ(·)为Heaviside函数

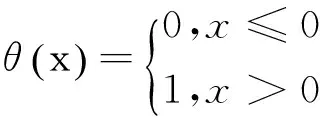
(3)当r→0时，关联积分与r存在以下关系：

上式参数r的选取需要考虑D能否描述奇异吸引子的自相似结构.

D=lnC(r)/lnr

维数D与函数C(r)需要满足对数线性关系，并且通过最小二乘法拟合，求出一条最佳直线，该直线的斜率即是对应于m0的关联维数的估计值d(m0).

(4)重复以上步骤(2)和(3)，继续增加嵌入维数m，直至关联维数d(m)不再随m的增加而增大，并且收敛于一个稳定值状态，此时求到的d值即为吸引子的关联维数.如果d值随m的增长而增长，并不收敛，则表明系统是随机的.

3 仿真实验验证

本次实验软件编程环境：Windows7；MATLAB7.0；硬件环境处理器: Intel(R) Core(TM)2 Duo CPU E4500 @2.20GHz.本实验采用记录累计失效时间来描述软件失效行为.首先收集公共测试(Beta)软件运行过程中的失效数据，然后通过MATLAB7.0语言编程，实现对失效数据关联维数的仿真，最后分析软件失效行为是否具有混沌性.

实验数据1[13]采用美国海军战术数据系统NTDS(Naval Tactical DataSystem)公开发表的失效数据.这些数据是从美国海军战术数据系统保存的一个实时多处理机系统软件开发过程的资料中提取的，包括38个不同的模块，每个程序模块都经过了开发阶段、测试阶段和使用阶段，数据见表1.

表1 NTDS数据集1
Tab.1 NTDS failure dataset 1

失效序号失效间隔/d失效序号失效间隔/d1918982211910433220105436211165432214964523156750242478582524996326250107027337117128384127729396137830405148731540159132798169233814179534849

实验数据集2[13]来源于Musa数据集，由Musa发表(Musa 1990).失效数据由实时命令与控制系统的测试得来，数据集2源于贝尔实验室，由9个程序员对包含21700条指令的系统的测试得来，系统运行时间为24.6 h，经历的日历时间为92 d.数据集包含了72个失效数据，描述了每个失效的CPU时间.整个失效数据集记录了失效发生的CPU时间，是失效时间数据集，具体见表2.

根据失效数据，利用G-P算法计算失效数据的关联维和嵌入维，部分编程如下：

G-P算法计算关联维数

form=min_m:max_m

Y=reconstitution(data,N,m,tau);

%重建矢量空间

M=N-(m-1)*tau;%矢量空间的点数

表2Musa失效数据集2
Tab.2Musafailuredataset2

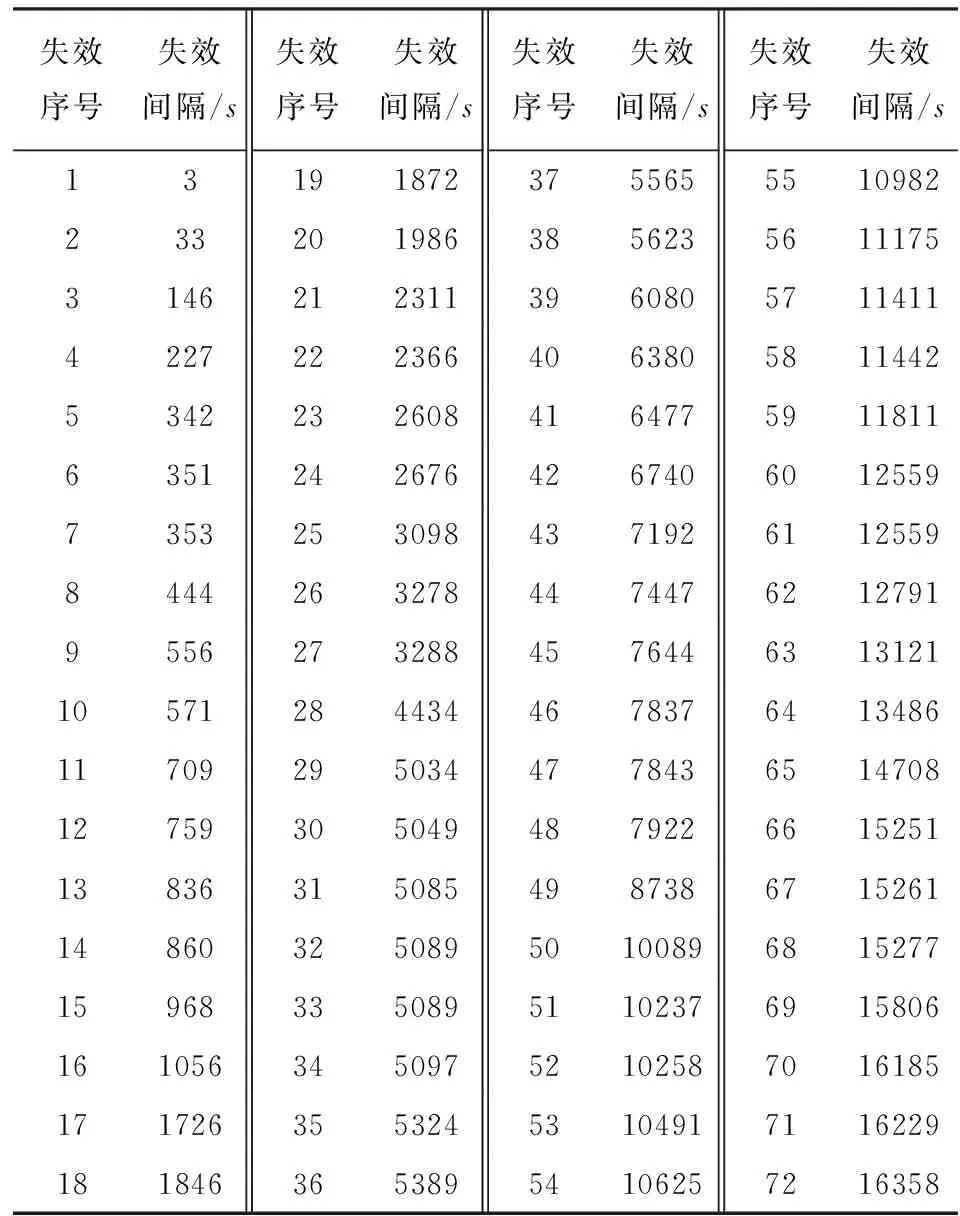
失效序号失效间隔/s失效序号失效间隔/s失效序号失效间隔/s失效序号失效间隔/s13191872375565551098223320198638562356111753146212311396080571141142272223664063805811442534223260841647759118116351242676426740601255973532530984371926112559844426327844744762127919556273288457644631312110571284434467837641348611709295034477843651470812759305049487922661525113836315085498738671526114860325089501008968152771596833508951102376915806161056345097521025870161851717263553245310491711622918184636538954106257216358

fori=1:M-1

forj=i+1:M

max(abs(Y(:,i)-Y(:,j)));

%计算其余点到点Xi的距离

end

end

max_d=max(max(d));%求出距离最远的点

d(1,1)=max_d;

min_d=min(min(d));%求出距离最近的点

delt=(max_d-min_d)/ss;%计算r的步长

for k=1:ss

r=min_d+k*delt;

C(k)=correlation_integral(Y,M,r);

%计算关联积分函数

ln_C(m,k)=log(C(k));%lnC(r)

ln_r(m,k)=log(r);%lnr

end

plot(ln_r(m,:),ln_C(m,:));

hold on;

end

使用Matlab软件工具运行NTDS 数据集1和Musa数据集2，结果分别如图1和图2所示.

图1 NTDS 数据的关联维数Fig.1 The correlation dimension of NTDS data

图1是NTDS 数据集的运行结果，关联维数d(m)随m的增加而增大，最终没有收敛于一个稳定值，并且关联维数中间有间断，说明系统是随机的.因此，NTDS 数据所表示的系统不具有混沌性.

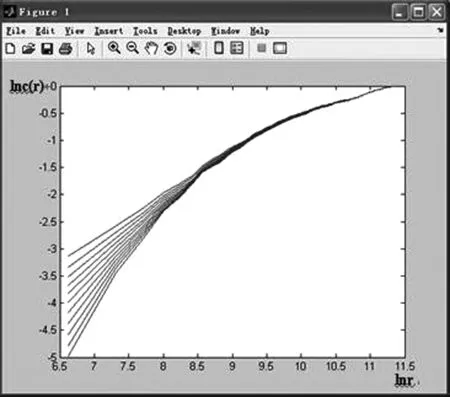
图2 Musa数据集的关联维数Fig.2 The correlation dimension of Musa dataset

图2是Musa数据集2的运行结果，关联积分曲线随着嵌入维m的增大而发生相应变化，对其进行线性拟合计算，求得关联积分曲线斜率就是关联维.关联维数d(m)随m的增加而增大，当m在[1-20]的范围内增长时，关联维d最终收敛于一个稳定值.因此，Musa数据集具有混沌性，表明了软件系统失效行为具有混沌性.

4 结束语

大数据环境下的软件失效行为不仅具有随机性，也具有确定性，软件失效行为的本质与混沌特性是具有相似性的，虽然受到确定规则的约束，但是其行为却表现出无序性.

本文提出一种基于关联维数的软件失效混沌识别算法，通过计算软件失效数据是否具有关联维特征来验证失效的混沌性，利用相空间方法来重构软件失效系统，定性定量地验证了软件失效行为的混沌性.实验表明，混沌特征量算法能够有效识别软件失效的混沌性，突破了软件失效分析一贯使用随机理论和数理统计方法的局限, 更加精准地描述大数据环境下的软件失效行为的无规则性和无序性，并且解决了软件失效、大数据混沌性等软件可靠性复杂问题，为大数据环境下的软件失效行为的研究带来了新的方法和思路.

[1]苗放.面向数据的软件体系结构初步探讨[J]. 计算机科学与探索,2016, 10(10):1351-1364.

[2]李国杰, 程学旗. 大数据研究:未来科技及经济社会发展的重大战略领域——大数据的研究现状与科学思考[J]. 中国科学院院刊, 2012, 27(6):5-15.

[3]汪北阳, 吕金虎. 复杂软件系统的软件网络结点影响分析[J]. 软件学报, 2013, 24(12):2814-2829.

[4]YANG J F, ZHAO M. Maximum likelihood estimation for software reliability with masked failure data[J]. Journal of Systems Engineering & Electronics, 2013, 35(12):2665-2669.

[5]程跃华, 崔艳. 组合模型在软件可靠性预测中的建模与仿真[J]. 计算机仿真, 2011, 28(6):371-374.

[6]刘克,单志广,王戟,等.“可信软件基础研究”重大研究计划综述[J]. 中国科学基金, 2008, 22(3):145-151.

[7]LIN C T, HUANG C Y. Enhancing and measuring the predictive capabilities of testing-effort dependent software reliability models[J]. Journal of Systems & Software, 2008, 81(6):1025-1038.

[8]楼俊钢, 蒋云良, 申情,等. 软件可靠性预测中不同核函数的预测能力评估[J]. 计算机学报, 2013, 36(6):1303-1311.

[9]INOUE S, HAYASHIDA S, YAMADA S. Toward Practical Software Reliability Assessment with Change-Point Based on Hazard Rate Models[C]//Computer Software and Applications Conference.IEEE Computer Society, 2013:268-273.

[10]LANDON J,OZEKICI S, SOYER R. A Markov modulated Poisson model for software reliability[J]. European Journal of Operational Research, 2013, 229(2):404-410.

[11]ZHENG J. Predicting software reliability with neural network ensembles[J]. Expert Systems with Applications An International Journal, 2009, 36(2):2116-2122.

[12]BARU C, BHANDARKAR M, CURINO C, et al. Discussion of BigBench: A Proposed Industry Standard Performance Benchmark for Big Data[M].[s.l.]:Springer International Publishing, 2014:44-63.

[13]LYU M R. Handbook of Software Reliability Engineering[M/OL].Hong Kong: Department of computer science and engineering, Chinese University Hong Kong,2005[2016-11-23].http://www.cse.cuhk.edu.hk/～lyu/book/reliability/.

Researchonthechaosidentificationofsoftwarefailurebehaviorbaseoncorrelationdimensioncalculation

QIAN Li，HU Jun，WANG Mei-rong,SHEN Gui-fang，CHEN Ping

(Institute of Information Engineering，Anhui Xinhua University, Hefei 230088, China)

In view of the disorder of software failure behavior in large data environment, a software failure identification method based on chaotic correlation dimension is proposed. With the help of the G-P algorithm, the characteristics of the correlation dimension and the embedding dimension of the failure data are calculated, and the uncertainty of the software failure data is determined by the chaotic characteristic quantity. The experimental results show that the chaos correlation dimension algorithm not only can effectively identify software failure,and accurately describe the software failure behavior disorder and irregular, but also can solve the complex software system failure, and big data chaos of this kind of complex problem.

big data； software failure；correlation dimension；chaos identification

2016-12-02

安徽省教育厅自然科学基金重点项目(KJ2014A100，KJ2015A300，KJ2016A304)；安徽省质量工程项目(2015ckjh113)

钱丽，女, wulianchongjing@qq.com

1672-6197(2018)01-0021-05

TP309.2

A

(编辑：姚佳良)