结合分数阶微分与结构张量的医学图像细微结构增强

王 宇，王远军，靳珍怡，方丽萍

1(上海理工大学 医疗器械与食品学院，上海 200093)

2(复旦大学 附属中山医院，上海 200032)

3(上海市影像医学研究所，上海 200032)

1 引 言

医学图像增强主要分为对比度增强和细微结构增强，常用的对比度增强算法有对数或指数变换、灰度拉伸线性变换、直方图均衡化和Retinex算法等.但是对比度增强只能改善图像的灰阶层次，而图像的纹理细节没有得到改善，这会影响到医生对病灶细节的判读和诊断，所以研究医学图像细微结构的增强具有重要的临床意义[1].目前常用的医学图像纹理结构细节增强方法根据不同增强方法原理特点，主要可以分为锐化增强、粗糙集模糊集增强[2，3]、多尺度几何增强[4]以及基于微分算子的增强方法[5-7]等.针对不同的医学图像成像特点，各种方法既有其优势也有其缺点，例如锐化增强可以增强图像的小细节以及边缘部分，但是对噪声比较敏感；模糊集增强虽然可以处理医学图像中大量的不确定性，得到较好的增强效果，但是需要依赖较多先验知识，鲁棒性低；多尺度几何增强可以从多个尺度对图像进行有针对性的增强，但容易产生“振铃”效应；基于微分算子的增强可以有效处理角点、管状等结构，但是Hessian矩阵的特征值与特征向量计算量大，影响处理效率.所以本文在这些方法的基础上，综合其优点，选取分数阶微分与结构张量相结合，希望可以对医学图像增强具有一般适用性，实现更优的细微结构增强效果.

结构张量首先被提出主要是用于数字图像处理，现已被广泛应用于图像增强[6，7]、分割[8]、融合[9，10]以及重建[11]等方面.结构张量是基于图像的梯度信息构建的一阶矩阵，结合图像的局部信息，可以获得比梯度特征更多的图像局部几何结构信息，即更好地描述图像的边缘、形状、角点等纹理结构信息[9，12].结构张量可以反映图像邻域内的像素变化特性，并且是由张量滤波后得到，因此结构张量对噪声具有更强的鲁棒性，可以提取出图像的稳定结构特征，有利于增强图像的纹理细节[13].尽管George[6]以及Moreno等人[7]结合扩散滤波使用结构张量可以有效增强医学图像中的管状结构，但是这些方法大多都是结合扩散方程以针对血管这种管状结构进行增强，而对分形样纹理以及边缘细节等特征没有详细描述.

传统的微分算子如Sobel算子、Prewitt算子是一阶边缘锐化算子，可沿水平方向和垂直方向锐化图像的边缘，Laplacian算子是二阶边缘锐化算子，对噪声比较敏感.这些算子都是整数阶微分运算，可以增强图像的高频边缘轮廓信息，但对图像纹理细节增强效果甚微.分数阶微分算子是整数阶微分运算的推广，研究发现，分数阶微分算子比整数阶微分算子更有利于分析和强化图像纹理细节信息[14，15].

结合上述结构张量与分数阶微分算子对图像纹理细节处理的优点，本文尝试将分数阶微分算子与结构张量相结合，构建基于分数阶微分算子的结构张量，从结构张量的特征值和特征向量可以研究所构建的分数阶局部图像描述算子对区分图像纹理不同结构区域特征的特性，从低频信号分数阶微分不为零的特点可以研究其对图像纹理的弱结构、小尺度以及结构信息的保持特性，在此基础上提出了结合分数阶微分算子与结构张量的医学图像细微结构增强的方法.在实验中，我们选取了包括计算机断层扫描(Computed Tomography，CT)和磁共振(Magnetic Resonance Imaging，MR)在内的多种模态的典型医学图像做了对比增强实验，并对实验结果分别进行定性和定量评价，结果表明本文提出的方法可以有效地增强图像的纹理细节，并能较好地保留图像的平滑区域以及弱纹理区域，具有良好的视觉效果，验证了该方法的有效性.

2 理论介绍

2.1 结构张量

定义二维图像I(x，y)：Ω→R2，I(x，y)表示点(x，y)处的灰度值，点(x，y)的梯度向量为▽I=(Ix，Iy)T，则输入图像的梯度可以在欧几里得空间RT进行说明[13]：

(1)

dI的平方范数可以表示成：

=(dxdy)G(dx

dy)

(2)

其中G的表达式为：

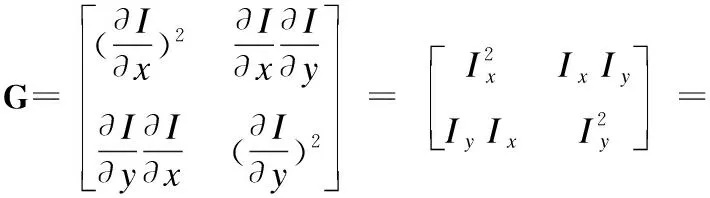
(3)

G即表示张量，T表示向量转置.通过公式(3)可以看出矩阵G是一个对称半正定矩阵，为了使其包含局部结构信息，通过滤波技术对张量场进行平滑，经过滤波平滑后的张量即为结构张量，表达式为：

(4)

gσ为方差是σ的高斯函数，*为卷积运算.矩阵的特征向量e1、e2表示该邻域内信号变化的方向，其非负特征值λ1、λ2表示沿这些方向变化的大小信息，可以反映图像的结构信息[16]：①若λ1≈λ2≈0，则表示图像在该点附近任何方向灰度变化几乎为0，可以认为是图像的平滑区域；②若λ1≈λ2>>0，则表明图像在该点无论是水平方向还是垂直方向变化率都很大，可以认为是图像的角点部分；③若λ1>>λ2≈0，则表示图像在该点附近的水平变化率要远远大于垂直变化率，可以认为是图像的边缘区域或流线区域.

根据特征值之间的关系可以进一步给出局部像素灰度值之间的相干性度量(Coherence)[17]来描述图像的局部信息，同时为了突出图像的纹理细节部分以及边缘区域，使之具有更好的结构表达能力，相干性度量Coh定义如下：

(5)

2.2 分数阶微分算子

分数阶微分增强图像主要是通过构建分数阶微分掩模算子，计算像素点及其邻域像素点关系的滤波增强.首先根据图像应用中最广泛应用的Grünwald-Letnikov(G-L)定义[18]，可推导出一维信号的分数阶差分表达式，然后在一维的基础上可推导出二维信号的分数阶差分表达式.

假设一维信号f(t)的持续时间为t∈[a，b]，通过取单位间隔h=1可将信号分成相等间隔，即m=[(b-a)/h]=[b-a]，则一维信号f(t)的α阶微分差分表达式为：

(6)

对于二维信号f(x，y)，因为像素点的最小间隔为1，根据公式(6)可以推导出f(x，y)在x和y方向的分数阶偏微分近似表达式：

(7)

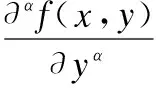
(8)

其中Γ(n)为Gamma函数，其定义为：

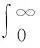
(9)

根据二维信号的分数阶表达式，可以发现分数阶微分要比整数阶微分连续性更好，对图像来说，纹理细节表达能力也要更好，连续性更强.根据不同方向上的系数取决于与中心像素点之间距离的关系，由此构建的八方向各向同性分数阶Tiansi 微分算子掩模模板如图1所示[15].在图像掩模计算时，对模板要进行归一化处理，对各项同时除以(8-12α+4α2).

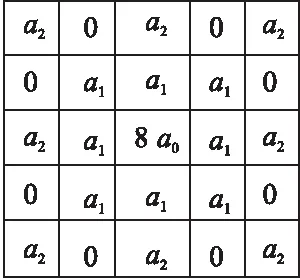
图1 Tiansi 微分算子模板Fig.1 Tiansi differential operator template

其中，a0，a1，a2分别定义如下：

(10)

2.3 基于分数阶微分算子的结构张量

由于纹理细节区域的整数阶微分值可能几乎接近零，而分数阶微分在处理图像纹理细节时，比整数阶更加精准.因此，将分数阶微分引入结构张量能更精确描述分形样纹理和边缘细节的特征，使之更加清晰连续.根据上述分析，α阶分数阶结构张量可以定义为：

(11)

为了尽量减小误差又不使运算量过大，选取公式(7)(8)中的前三项做差分运算，所以：

(12)

(13)

3 实验结果与讨论

由于图像的细微结构主要是图像的高频信息，根据小波变换可将图像分为近似信息的低频部分以及包含细节的高频部分，本文将结合小波变换实现具体算法.对图像来说，利用小波分解后得到的低频信息主要是图像变化缓慢的区域，即图像主要轮廓部分[19]，我们可利用Tiansi微分掩膜算子对低频信号进行处理，加强图像轮廓的提取；分解后得到的高频信息主要是图像变化迅速的区域，反应图像的细节信息，主要分为水平、垂直和对角线三个细节子带，利用分数阶结构张量可以描述更丰富的局部细节信息，然后可根据加权各高频分量得到具有更清晰连续的纹理细节的高频信号.根据上述分析，整个实验的算法流程图如图2所示.

图2 算法具体流程图Fig.2 Detailed algorithm flow chart

流程图中H，V，D分别代表小波分解后水平、垂直和斜对角方向的高频分量；Coh表示高频分量的相干性度量，是根据高频分量的分数阶结构张量的特征值构造而成，三个高频分量的相干性度量分别为CohH，CohV，CohD；HVD表示为加权各高频分量后得到的最后高频分量，具体定义为：

(14)

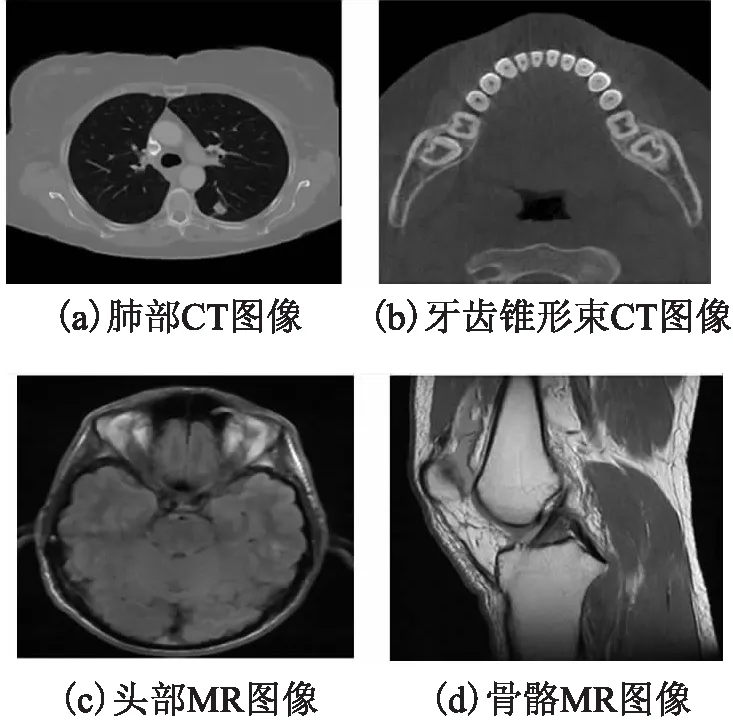
图3 实验原图Fig.3 Experiment original images

为验证算法的自适应性，我们选取了不同模态不同解剖部位的医学图像作为增强实验的原图像，具体如图3所示，其中(a)是肺部CT图像，(b)是牙齿锥形束CT图像，(c)是头部MR图像，(d)是骨骼MR图像.我们以MATLAB2016b为平台进行算法验证，选取结构张量增强、整数阶微分算子(Sobel微分算子)增强、分数阶微分算子(Tiansi算子)增强[15]、以及自适应分数阶增强[20]作为对比实验，结构张量增强方法主要是对高频分量构造的结构张量，然后再根据相干性度量加权，低频部分不做任何处理.实验中用到的分数阶次均选取α=0.6.具体实验结果如图4-图7所示.

图4是肺部CT图像的增强效果对比图，其中(a)是实验原图，(b)是本文方法得到的增强实验结果图，(c)表示的是结构张量方法得到的增强实验结果图，(d)表示的是整数阶Sobel微分算子增强方法得到的增强实验结果图，(e)表示的是文献[15]中分数阶Tiansi微分算子增强方法得到的增强实验结果图，(f)表示的是文献[20]中自适应分数阶增强方法得到的增强实验结果图.对比各实验结果图可以发现，特别是针对图(a)中标出的感兴趣区域，(b)图中的肺部血管增强较为明显，且病灶的边缘轮廓也有所增强，图像更加清晰；(d)图和(e)图中，血管的清晰度也有所相应的增强，但整体视觉效果不如(b)图；而(f)图中，文献[20]方法出现了较为严重的失真现象.

图4 肺部CT图像增强效果对比Fig.4 Effect contrast of lung CT image enhancement

图5 牙齿锥形束CT图像增强效果对比Fig.5 Effect contrast of tooth cone beam CT image enhancement

图5是牙齿锥形束CT图像的增强效果对比图，其中(a)是实验原图，(b)是本文方法得到的增强实验结果图，(c)表示的是结构张量方法得到的增强实验结果图，(d)表示的是整数阶Sobel微分算子增强方法得到的增强实验结果图，(e)表示的是文献[15]中分数阶Tiansi微分算子增强方法得到的增强实验结果图，(f)表示的是文献[20]中自适应分数阶增强方法得到的增强实验结果图.对比各实验结果图可以发现，相对(a)图中感兴趣区域中的切牙、前磨牙和磨牙部分，(b)图中牙齿的边缘轮廓相比更为清晰，有利于进一步的分割等后续处理；(f)图虽然增强效果不明显，但是有效的去除了噪声，具有良好的去噪效果.

图6是头部MR图像的增强效果对比图，其中(a)是实验原图，(b)是本文方法得到的增强实验结果图，(c)表示的是结构张量方法得到的增强实验结果图，(d)表示的是整数阶Sobel微分算子增强方法得到的增强实验结果图，(e)表示的是文献[15]中分数阶Tiansi微分算子增强方法得到的增强实验结果图，(f)表示的是文献[20]中自适应分数阶增强方法得到的增强实验结果图.从图6(b)可以看出，本文方法对头部MR图像有增强效果但不如之前CT图像增强效果明显，主要是因为头部MR图像的高频信号相对较少，所以此方法得到的图像增强效果不太明显.

图6 头部MR图像增强效果对比Fig.6 Effect contrast of head MR image enhancement

图7是骨骼MR图像的增强效果对比图，其中(a)是实验原图，(b)是本文方法得到的增强实验结果图，(c)表示的是结构张量方法得到的增强实验结果图，(d)表示的是整数阶Sobel微分算子增强方法得到的增强实验结果图，(e)表示的是文献[15]中分数阶Tiansi微分算子增强方法得到的增强实验结果图，(f)表示的是文献[20]中自适应分数阶增强方法得到的增强实验结果图.从图7中可以看出，针对(a)图中标出的感兴趣区域，(b)图中肌肉纹理以及与骨头连接处韧带的纹理细节相比其他图像增强效果更加明显，图像的细微结构更加清晰，图(c)(d)(e)相比较原图也有增强效果，其中(d)图主要是增强了图像的边缘轮廓.(b)(d)(e)图中都不可避免的增强了噪声，而(f)图中对噪声的鲁棒性较强.

对图4-图7总体对比发现，本文方法的增强效果在图4(b)、图5(b)和图7(b)中表现较明显，说明本文提出的结合分数阶微分算子与结构张量的增强方法在增强图像轮廓边缘的同时可以有效的增强图像细微结构，具有良好的视觉效果；从图4(d)-图7(d)和4(e)-图7(e)之间对比可以看出，Sobel算子虽然和Tiansi分数阶算子均可以不同程度的增强图像的细节，但是Sobel算子增强图像主要是锐化图像边缘轮廓，其中以图5(d)、图6(d)较为明显，而Tiansi 分数阶算子则主要侧重于增强图像的纹理细节部分，其中以图4 (e)和图7 (e)较为明显，说明分数阶微分算子在纹理细节增强上要优于整数阶微分算子.

为了进一步说明本文方法的有效性，将信息熵(Entropy)，平均梯度(Meangradient)以及对比度改善指数(Contrast Improvement Index，CII)作为图像纹理细节增强定量评价指标，结果如表1-表4所示.其中信息熵，平均梯度以及CII定义如下：

1)信息熵是衡量图像信息丰富程度的一个重要指标.图像的信息熵越大，则图像中包含的信息量越丰富，图像的边缘和纹理细节越明显.图像熵的定义为：

H(p)=-∑p(i，j)logp(i，j)

(15)

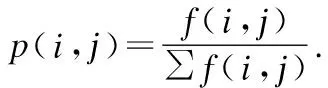
2)平均梯度又称为清晰度，反映了图像中的微小细节反差与纹理变化特征，同时也反映了图像的清晰度.其定义为：

(16)

式中ΔIx与ΔIy分别为x，y方向上的差分.

3)CII用来衡量图像的整体对比度，反映图像整体和细节的增强效果.CII值大于1，表明有增强效果，值越大，表明图像细节信息增强越明显，且具有良好的视觉效果.其定义如下[21]：

(17)

Cproposed和Coriginal分别为增强后图像和原图像的局部对比度.C定义为：

(18)

分析表1-表4中数据可以看到，本文提出的方法在平均梯度参数值上约是原图的2倍，说明本文方法有效增强了图像中的纹理细节部分，增强了图像的清晰度；同时可根据信息熵参数发现，本文方法对应增强图像的信息熵也有相应的增加，可以说明该方法丰富了图像信息，有效的保留了图像平滑区域以及弱纹理区域；另外从对比度改善指数也可以发现，本文提出的方法CII值是对比方法中最高的，说明本文方法增强的图像具有良好的视觉效果.从这三个指标可以总结出，结合分数阶与结构张量增强的图像具有分数阶增强以及结构张量增强两方面的优势，相比较单一的分数阶增强方法而言，分数阶结构张量增强的图像噪声比较小，图像信息丰富程度也较高；而相比较单一的结构张量增强方法，分数阶结构张量可以更加清晰的表达图像纹理细节.整体实验说明本文提出的方法可以有效的增强图像的纹理细节，并能较好的保留图像的平滑区域以及弱纹理区域，具有良好的视觉效果.尽管在表3和表4中，针对MR图像，文献[20]方法增强图像得到的信息熵值较为突出，主要是文献[20]方法具有良好的去噪效果，但图像的平均梯度值以及CII值都相比较低，图像的清晰度不够好.再者，从视觉评价上结构张量增强图像效果不明显，但是从客观指标上还是可以看出结构张量增强方法对图像的纹理细节还是有增强效果的.

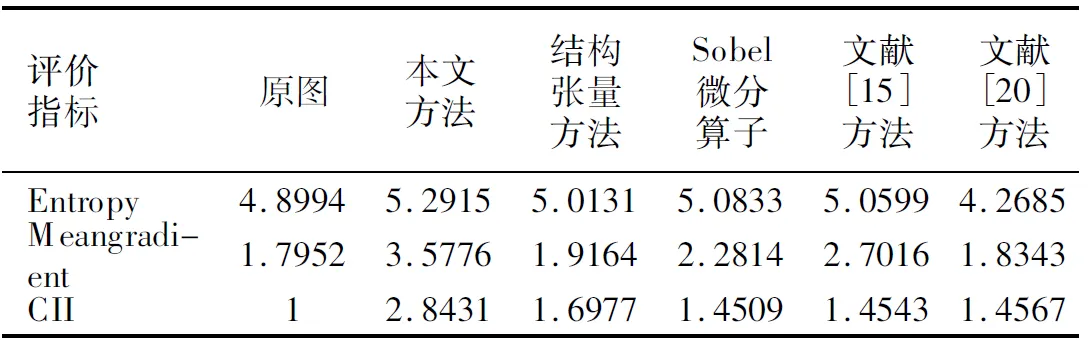
表1 图4中各图像评价参数

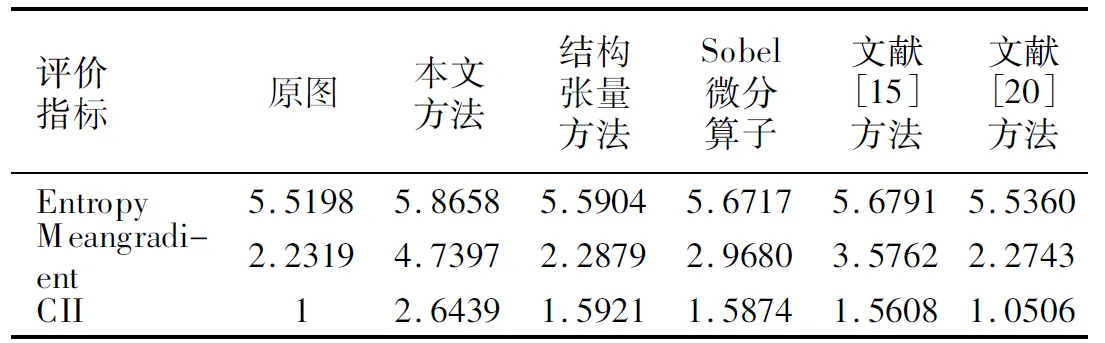
表2 图5中各图像评价参数Table 2 Evaluation parameters for each image in fig.5

表3 图6中各图像评价参数Table 3 Evaluation parameters for each image in fig.6

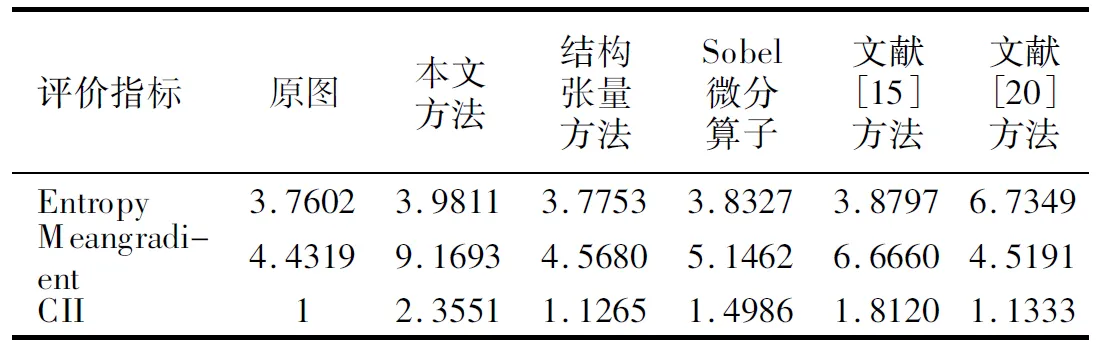
表4 图7中各图像评价参数

为了更直观的表观各图像评价参数，做出了各表中评价参数的折线图，具体如图8-图11所示.从折线图中可以看出，与对比实验方法以及原图相比，本文方法具有明显的高峰走势.

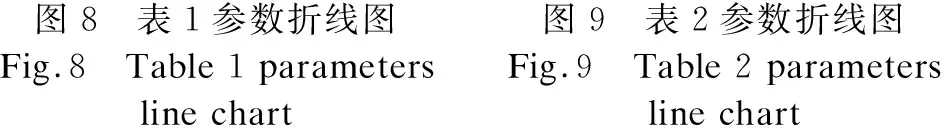
图8 表1参数折线图Fig.8 Table 1 parametersline chart图9 表2参数折线图Fig.9 Table 2 parameters line chart

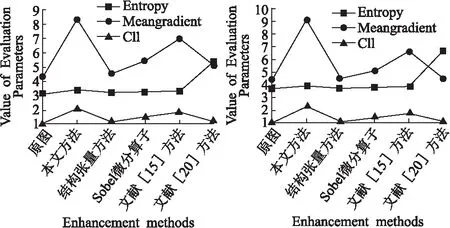
图10 表3参数折线图Fig.10 Table 3 parametersline chart图11 表4参数折线图Fig.11 Table 4 parametersline chart

4 结束语

本文提出了一种结合分数阶微分和结构张量的医学图像细微结构增强方法.在基于小波分解的基础上，低频信号通过分数阶微分算子锐化增强其图像整体轮廓，高频信号通过构建的分数阶结构张量的特征值之间的相干性度量加权以加强其纹理细节的清晰连续性，最后重构得到增强后的医学图像.通过对不同的CT图像和MR图像进行实验，验证了该方法的有效性.实验表明本文方法要比分数阶微分增强方法得到更丰富的图像信息，要比结构张量增强方法得到更加清晰连续的纹理细节，且细微结构的增强相对明显，有着良好的视觉效果，说明此方法具有良好的临床潜力.但此方法中只用到了结构张量的特征值，对于表示图像局部灰度变化方向的特征向量还没有加以应用，在后续的细微结构增强中需要做进一步研究.