一种基于改进粒子系统的池火灾实时渲染方法

苏 谟,郭锐锋，王丽丽，王鸿亮，马元婧，赵玉彬

1(中国科学院大学，北京 100049)

2(中国科学院 沈阳计算技术研究所， 沈阳 110168)

1 引 言

池火灾是一种常见的火灾形式，是可燃液体的自然燃烧.可燃液体(如汽油、柴油等)泄露后流到地面形成液池，遇到火源燃烧而成池火灾[1].随着石油、化工等行业的发展，可燃性液体的生产、使用、存储等过程越来越多.可燃性液体一旦发生泄漏，很容易形成池火灾并发生严重的事故[2].本文以环境空气质量预警平台项目为背景，研究池火灾实时模拟对事故后果模拟分析及事故风险评估尤为重要，同时实时地模拟真实感火焰一直是计算机图形学的难点之一.

目前，池火的模拟方法主要有三种途径，分别是基于粒子系统、数学物理模型和纹理贴图方式.基于数学物理模型模拟是将火焰视为一种特殊的流体，采用NS(Navier-Stokers)方程求解火焰运动，这类方法需要求解一系列复杂的非线性NS方程，但求解计算量大，难以满足实时性要求[3].郭燕[4]等人，采用外形轮廓与纹理贴图相结合的方法生成燃烧的效果，这种方法仅构造一个二维的符合一定规律的火焰效果，但很难与周围的环境发生交互作用及影响火焰动态变化的呈现.粒子系统理论是迄今为止用于描述不规则物体最成熟的理论之一.许多国内外研究学者采用基于粒子系统的火焰模拟方法，但粒子的控制过程过于随机，单纯使用粒子系统无法精确描述燃烧的池火.张亮[5]等人将火焰运动模拟函数融入到粒子系统中实现较好的火焰模拟效果.但未考虑环境因素且影响火焰模拟效果的物理参数有限.刘刚[6]等人采用CUDA平台加速粒子属性的更新速度，降低CPU和GPU之间频繁通信，提高了渲染速度，但粒子运动模型未考虑边界碰撞检测，而这部分需要消耗大量的计算资源，本文采用CUDA的并行计算架构对粒子状态更新加速并对池火边界碰撞检测进行优化加速.

综上，基于数学物理模型的方法难以保证池火实时模拟，而纹理贴图技术受纹理选择的影响易造成模拟缺乏真实感.本文提出一种基于改进粒子系统的池火灾实时渲染方法，针对粒子系统模拟火焰过于随机的缺点，综合文献[1,2]构建池火数学模型(考虑了环境影响因素)，借鉴文献[4]思路，将池火数学模型融入粒子系统，形成了改进的粒子系统模型，引入基于自适应二叉树的剖分算法对燃液碰撞检测，通过CPU-GPU协同及GPU并行加速实现实时渲染真实感的池火灾，本文为池火灾的模拟提供了新思路，具有实际应用价值.

2 池火灾模型

在传统的研究池火灾模拟分析过程中，形成了很多理论与经验的数据，运用池火灾数学模型，模拟池火燃烧速率、火灾发生时的液池半径、火焰高度、火焰燃烧时间等物理量随时间、距离的变化过程.

2.1 池火燃烧速率

Babrauskas在进行大规模池火实验基础上，提出了池火的燃烧速率估算公式[1]，考虑了液池大小后如公式(1)所示：

mf=mmax[1-exp(-2σβR)]

(1)

其中：mf—可燃液体的质量燃烧速率，kg/(m2·s)；mmax—可燃液体的最大质量燃烧速率(mmax)，kg/(m2·s)；σ—火焰的吸收衰减系数，(m-1)；β—平均光线长度校正系数；R—液池半径.几种常见油品的mmax和σβ值如表1所示.

表1 常见燃液的mmax和σβ值Table 1 Value of mmax and σβ of fuel

2.2 液池半径

考虑到液体的部分流出，假设液体的泄露点为中心呈扁圆柱形的光滑平面上扩散，这时液池半径R用一下公式计算：

1)瞬时泄漏(泄漏时间不超过30s)时，半径见公式(2)：

(2)

2)连续泄漏时半径如公式(3)所示：

(3)

式中：R—液池半径，m；M—泄漏的液体量，kg；ρ—液体的密度，kg/m3；g—重力加速度，g=9.8m/s2；t—泄漏时间，s；部分可燃液体密度：

表2 部分可燃液体密度Table 2 Some fuel density

对于无边界阻挡的连续泄露，随着液池面积扩大燃烧速度加快，当燃烧速度等于泄露速度时，液池半径达到最大，具体公式(4)如下：

(4)

其中Rmax—液池半径,(m)；Q液体泄漏流量，(km/s)；mf液池单位面积燃烧速率， (kg/(m2·s)).

2.3 池火高度

计算池火高度，通常使用Thomas关系式，它是以物理原理和实验量为基础的[2]，公式(5)如下：

(5)

其中：L—火焰高度，(m)；R—液池半径，(m)；ρa—空气密度，ρ0=1.297(kg/m3)；g—引力常数，g=9.8m/s2；mf—燃料的燃烧速率， (kg/m2·s).

2.4 池火持续时间

(6)

公式(6)中，W为剩余燃料的质量，kg.

3 改进的粒子系统模型

池火灾在燃烧过程中与传统火焰燃烧存在一定程度的差异.在使用传统粒子系统模拟池火灾燃烧过程基础上，本文结合池火灾模型，融入池火灾燃烧过程的特点，通过对发射器发射面的形状与面积、发射器发射粒子的高度、发射器发射粒子的速度变化、火焰的颜色、粒子的初始位置重新定义，并考虑了池火与环境障碍物碰撞检测，建立了改进的粒子系统模型.

3.1 粒子系统的定义

定义1.单个粒子定义为在实数域的一个s维向量，表示为：

Ps={prop1,prop2,…,propi,…,props|s∈N}

(7)

其中prop1,prop2,…,propi,…,props是粒子的s个属性，通常粒子的属性包括空间位置，粒子大小、形状、运动速度和加速度、颜色、亮度、生存周期等.单个粒子是组成粒子系统的基本元素.

定义2.粒子映射是单个粒子到正整数集的关系映射，每个粒子都具有唯一的索引，表示为It到ps的映射：

S(t)={It→Ps|It⊂Z+,s∈N,t∈R+}

(8)

其中，W(i)=Ps表示索引为i的粒子的状态和性质.

定义3.粒子系统是粒子映射集的有限集合，表示为：

F(t)={S(t)|t∈{t0,t1,…,tm}}

(9)

公式(9)中，F为粒子在系统时刻在t0,t1,…,tm的状态集合，S(t0)是初始状态下粒子系统状态[7].

3.2 基于池火灾的粒子系统模型

根据粒子系统的特点，结合池火灾模型，建立池火燃烧速率、液池半径、火焰高度及火焰持续时间等物理量与粒子系统渲染池火灾关键参数的关系，形成基于池火灾的粒子系统模型.

中共中央党校(国家行政学院)教授车文辉以《生态文明视域下的乡村振兴》为题，重点阐述了乡村振兴战略实施过程中的生态文明建设问题，指出了乡村建设、经济开发进程中忽视生态、破坏生态的现象以及带来的严重后果，提出生态建设、生态保护是乡村振兴题中应有之义，生态文明好不好决定着乡村振兴的质量。

3.2.1 发射器发射面的形状与面积

在池火灾发生的时候，整个液池都会持续的燃烧，此时火焰是包围在整个液池的表面，液池表面的面积和形状作为发射器发射面的形状和面积约束依据，基于假设液池周围没有狭长缝隙等特殊地形，采用圆柱形液池模拟液池形状，发射面面积S为公式(10)所示：

S=πR2+Cs(0≤R≤Rmax)

(10)

其中R为池火灾模型中液池的半径，CS液池与周边环境发生碰撞检测时所影响液池的面积.

3.2.2 发射器发射粒子的高度

发射器发射粒子的高度如公式(11)所示：

H=βLmaxβ∈(0,1]

(11)

其中Lmax为当液池半径为R时通过mmax求得的火焰最大高度值.通过β值的分布函数计算火焰在燃池中的高度变化.考虑到火焰的收拢趋势，即大部分火焰在不受外界干扰的情况下，均向中心收拢且中心点的火焰高度最高，向四周方向高度递减.本文使用正态分布函数来设定β值，使用正态分布计算β，则β值可以使用公式(12)得到：

(12)

其中xp和yp为粒子在初始化点的坐标x和y值,λ跟火焰的燃烧时间有关，y是正态分布函数.由公式(6)可知，池火继续燃烧时间跟火焰高度的关系可以使用公式(13)进行控制：

λ=1-e-∂t

(13)

3.2.3 发射器发射粒子的速度变化

池火粒子的运动与受力分析基于如下假设：

1) 池火粒子可以被视为理想的质点.

2) 风力在整个模拟过程中保持不变.

3) 池火粒子受到的力仅包括重力、风力及空气阻力的影响(非主要作用力忽略不计).

根据流体力学和空气动力学，池火粒子在空气中受到空气阻力的作用，包括牛顿阻力、摩擦力和粘滞力三个力，计算空气阻力的经验公式(14)如下[10]：

(14)

其中，S为粒子的投影面积(取1cm2)，ρ表示空气密度(取1.29kg/m3)，Cd表示阻力系数(取0.47)，为方便微分方程求解，采用空气阻力与速度系数的正比关系式为公式(15)所示.

F=kv

(15)

其中k为空气阻力系数(通过经验公式计算空气阻力的比例系数k≈3.03×10-6)，v为粒子运动速度.

根据牛顿第二定律，分析池火粒子的受力情况和加速度可得公式(16)：

ma=-mg-kv

(16)

分量表达形式：

(17)

通过积分计算的粒子各个分量上的速度变化可得：

(18)

为了体现粒子运动的随机性，在初始速度基础是添加一定的随机偏移：

V0=Vinit·rand(0.9,1.1)

(19)

其中Vinit是通过动量守恒定理求得的速度近似下限，粒子速度在上升的过程中粒子遵循动量守恒原则，粒子的初始速度需要达到一个下限的值之后才能运动到最高点，求解空气阻力做功较复杂，可以使用近似解来求出空气阻力做功，具体可由动量守恒公式(20)所得.

(20)

综上，最终加上风的效果，粒子的速度变化如公式(21)所示结果：

V′(t)=V(t)+Vwind

(21)

3.2.4 池火颜色模型

颜色是一个非常重要的物理属性，通过建立池火颜色模型来提高池火渲染真实感，采用线性插值和颜色渐变两种方式混合来设定池火粒子的颜色.选择粒子上升阶段总高度的0→α范围内使用颜色的线性插值，设定α(0,1)值(常用的α值可根据应用渲染需要形成配置策略).在粒子上升总高度的α→1的范围内使用颜色渐变，颜色模型使用RGBA模型，其中R、G、B分别代表红、绿、蓝分量，A代表透明度.

在粒子上升总高度0→α的范围内线性插值计算为公式(22)：

(22)

在公式(22)中，O(r,g,b)池火最底部，即初始池火粒子时的颜色值，M(r,g,b)是在火焰高度α处取得的颜色值减去O(r,g,b)得到的颜色的变化范围，L为粒子根据位置计算得到的能上升的最大高度.h为粒子当前的高度粒子在上升总高度.α→1的范围内使用颜色渐变，改变A的值从1→0，从而最终消失计算为公式(23)：

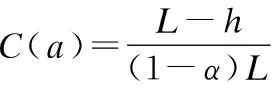
(23)

3.2.5 池火粒子初始数量

池火粒子数量决定了池火的密度，池火粒子数量也是影响可视化实时性的重要因素，池火粒子数量过小池火渲染会失真，本文采用公式(24)来确定池火粒子的数量：

(24)

其中meannum是屏幕单位区域内产生单位粒子数目的平均值，方差为varnum，Area为显示区域， 为粒子大小.

3.2.6 池火粒子初始位置

池火粒子的初始位置决定了粒子表现火焰的密度分布，经典粒子系统中，粒子位置初始化的方法具有普遍性而不具有针对性，针对池火焰的边界粒子稀疏，中心密集的特点，并且成正态分布，本文采用高斯分布(正态分布)与随机数相结合的方法确定新粒子的初始位置.设粒子的初始位置为

I(t0)=Position={Xi(t0),Yi(t0),Zi(t0)},1≤I≤numb0

粒子的分布，燃点位于XOZ平面，从该平面向上燃烧(y正方向)，R′为燃烧区域半径，则火焰粒子的分布可用公式(25)表示：

(25)

3.3 池火与环境障碍物碰撞检测

池火与环境障碍物的碰撞检测需要检测粒子在运动过程中是否与环境障碍物发生碰撞，该问题可以转化为粒子在时间间隔内所经过的路径是否与环境障碍物发生碰撞.由于时间间隔比较短，因此粒子的运动轨迹可近似为一条线段.因此将粒子与环境障碍物的碰撞检测问题转化为线段与三角面片的相交检测问题.假设场景有M个三角面片，N个粒子，其时间复杂度为O(M×N).

图1 池火与环境障碍物碰撞检测流程图Fig.1 Collision test between pool fire and environmental obstacle

为了提高碰撞检测算法的效率，本文根据粒子与环境障碍物的空间相关性，采用ABT空间剖分算法和层次包围盒技术，ABT空间剖分算法在分割平面(由一个考虑了多种不同参数如分割面的数量和位置等的评分系统决定)的选择上更科学、合理，从而减少需要检测的三角面数，节省内存空间，提高算法的效率.算法流程如图1所示.

4 基于GPU的粒子系统实现模型

在改进的粒子系统模型的基础上，本文采用基于GPU的粒子系统实现模型，利用CPU-GPU协同及GPU并行加速满足实时性渲染的要求.

4.1 基于GPU的改进粒子系统

本文围绕粒子系统构造过程，即粒子产生、粒子属性更新、粒子销毁和粒子绘制4个阶段[8]，提出基于GPU的改进粒子系统模型，如图2所示，通过CPU和GPU协同方式实现池火实时渲染，能够减少CPU和GPU之间的频繁通信及系统内存和显存间的频繁数据传送，降低CPU负担[9].在CPU端主要任务包括粒子系统初始化参数设置，建立基于池火灾的粒子系统模型，粒子产生及销毁.鉴于GPU的高并行性和可编程性，将池火粒子属性更新、池火与环境障碍物的碰撞检测和池火粒子绘制在GPU端实现，以满足实时性渲染要求.

4.2 基于GPU的算法实现框架

为了提高池火实时渲染效率，并结合基于GPU的改进粒子系统模型，本文提出了具体的基于GPU的算法实现框架，减少CPU和GPU的通信，实现GPU通用计算和渲染的结合，达到实时渲染池火的目的.如图3所示，在CPU端主要实现初始化粒子系统参数、分配存储空间(标量/矢量等)及围绕交互应用的粒子系统逻辑控制工作.通过将粒子初始数据传输至GPU显存后，由GPU端完成重要的计算和绘制工作.在GPU端主要实现基于池火灾的粒子系统模型的计算、迭代更新池火粒子运行状态、池火边界碰撞检测以及池火绘制工作.将计算的顶点数据直接用于GPU的渲染，利用CUDA架构的并行计算能力，将每个粒子映射到GPU处理器的每个线程，将粒子属性数据存放在全局存储器，每个线程块中的各个线程唯一对应于全局存储器中对应的一个粒子属性数据，不同线程块中的不同线程读取显存中全局存储器中对应粒子的属性数据进行更新计算[10].通过着色器纹理、顶点、光源等数据整合处理后进行粒子的绘制.

图2 基于GPU的改进粒子系统模型图Fig.2 GPU-based improved particle system model

5 实验结果与分析

本实验硬件配置：CPU Intel Core(TM)i3-4160 3.6GHz，四核处理器，内存为8GB，显卡型号为NVIDIA GeForce 9600 GT，显存为1GB.

软件平台为Windows 7旗舰版64位操作系统，开发语言为C++，开发工具为Visual Studio 2013，OpenGL 4.3版本，OSG3.2.3版本，NVIDIA驱动版本号为174.16.

图4给出了采用本文池火灾实时渲染方法的效果图，采用实验数据(保留一帧的截图)，当前池火燃烧速率为0.39(kg/m2·s)、燃烧物质为煤油、池火半径为17.21m、池火高度12.32m.经典粒子系统模拟火焰的过程，粒子的随机运动一定程度上影响了火焰的真实感，本文通过引入池火灾模型作为粒子系统构造的基础，通过建立基于池火灾的粒子系统模型对粒子运行状态控制，更贴近池火应用场景.本文基于GPU的粒子系统实现模型，确保池火实时渲染效率，当前渲染的顶点数1.8M，三角形面数1.6M，帧率达到53.6fps.

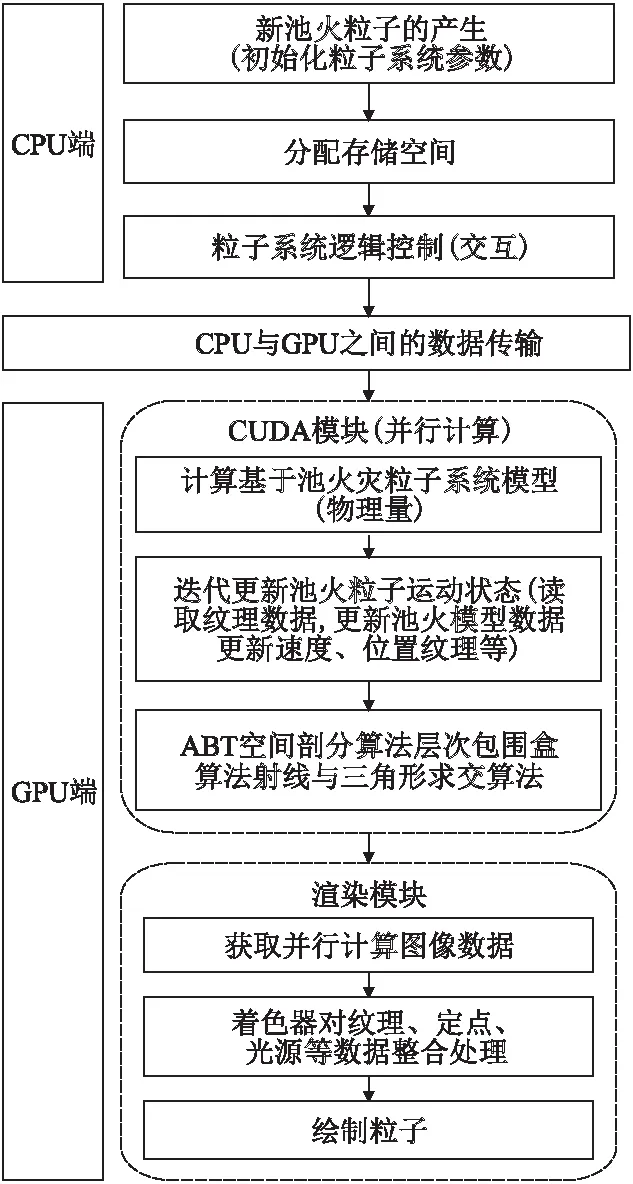
图3 基于GPU的算法实现框架图Fig.3 GPU-based algorithm implementation framework

图4 池火灾模拟效果图Fig.4 Pool fire simulation results

图5 采用文献[5]方法模拟出池火灾效果图Fig.5 Pool fire effect via literature[5]

图6 改进粒子系统的池火效果图Fig.6 Improved particle system pool fire effect

图5是采用文献[5]方法模拟池火灾效果图，由于未考虑环境因素且影响火焰模拟效果的物理参数有限，火焰效果粗糙.图6是采用改进的粒子系统模型后池火灾效果图，本文构建的池火灾模型引入池火燃烧过程的关键物理量，并考虑环境因素影响如风力对池火的影响，在燃烧过程中出现火焰聚拢效应，火焰真实感增强，池火的形态会随风力变化而实时渲染.

图7是采用文献[4]算法模拟池火边界碰撞效果图，采用层次包围盒算法来进行碰撞检测，图8为采用本文算法模拟池火边界碰撞效果图，由于采用了ABT空间剖分算法和层次包围盒算法相结合方式，可有效进行边界检测并作出碰撞反应.

图7 文献[4]算法的池火边界碰撞效果图Fig.7 Boundary collision effect via literature[4]

图8 本文算法的池火边界碰撞效果图Fig.8 Boundary collision effectvia our method

在文献[6,8]仅使用CUDA架构加速粒子属性的更新，本文在GPU端实现迭代更新池火粒子运行状态和计算池火边界碰撞检测.分别用35000、400000个池火粒子来验证本文算法同使用 CPU 计算在性能上的差异，渲染速度结果如表3所示.

表3 渲染速度对比图 Table 3 Rendering speed comparison

从表3可以看出，在帧率和每帧绘制的三角面片数量上，本文提出的池火渲染方法比传统CPU实现池火渲染效果更好.在渲染35000个池火粒子时传统CPU平台下可达到平均 30.4帧/秒，基本满足实时交互能力.但当池火粒子数增加至400000个时，传统CPU平台下的 FPS 减少到了平均14.1帧/秒.而采用本文的算法在CUDA平台下仍然可以达到平均 64.4帧/秒，计算速度是传统CPU平台的4倍多.因此，与传统CPU实现的算法相比较，本文提出的算法CPU的占用率大大降低，降低CPU计算负载，满足实时性的要求.

6 结束语

本文提出一种基于改进粒子系统的池火灾实时渲染方法，将池火灾数学模型融入到粒子系统，建立了改进的粒子系统模型，并综合考虑外力环境因素及池火边界的碰撞检测.采用基于GPU的粒子系统实现模型，利用GPU强大的并行计算能力对粒子状态更新加速，并使用基于自适应二叉树的剖分算法对池火边界碰撞检测进行优化实现加速，有效减少了内存和显存之间的数据传输，从而实现池火灾实时渲染过程优化，使性能得到显著提高，解决了池火灾模拟难以实现实时性和真实感的问题.