自适应局部半径的DBSCAN聚类算法
秦佳睿,徐蔚鸿,马红华,曾水玲
1(长沙理工大学 计算机与通信工程学院,长沙 410114)
2(湖南省资兴市科学技术局,湖南 郴州 423400)
3(吉首大学 信息科学与工程学院,湖南 吉首 416000)
1 引 言
聚类分析能够从给定数据集中发现数据元素间的潜在联系,挖掘感兴趣的知识.基于密度的聚类分析方法(以下简称为“密度聚类”)能够在簇(cluster)个数未知的情况下,完成对形状不规则的、具有噪声的数据集的聚类.由于这一特点,基于密度的聚类分析方法在电子商务、市场活动、地理预测、模式识别等多个领域得到广泛应用[1,2].
DBSCAN(Density-Based on Spatial Clustering of Application with Noise)算法[5,6]是一种经典的基于密度的聚类分析算法.该算法需要用户设定领域最小点数minPts和邻域半径eps两个参数.这两个参数的取值,对于聚类结果的影响非常大.户不具有应用领域的先验知识时,往往难以选择确定合适的参数.同时,在整个聚类过程中,这两个参数是不变的,因此在数据集密度不均匀或噪声干扰较大的情况下,聚类结果的精确度会有所降低.
针对DBSCAN算法的上述问题,国内外许多学者提出了不同的改进方法.DBSCANCC[7]算法通过记录簇连接信息的方法减小参数选择的范围,但该方法仍未实现参数的自适应调整.OPTICS-PLUS算法[8]通过有效的结果重组织策略,以辅助稀疏点的重新定位,并采用针对文本领域的特点的距离度量方法,但该方法仍未解决多密度数据集的聚类问题,而且算法时间复杂度也非常高.I-DBSCAN算法[9]根据数据集本身的统计特性,通过对距离分布矩阵的观察确定参数,但该方法在获取参数过程中存在误差导致聚类结果的准确性不能满足要求.Greedy-DBSCAN算法[10]通过贪心策略自适应确定邻域半径eps参数,该算法实现了自适应确定局部最优eps,并通过邻域内点间平均距离与确定的eps参数的比较发现噪声,但该方法难以确定噪声判定所需的阈值参数.文献[11]中提出一种基于局部密度峰值进行聚类的方法,该方法通过发现数据集中局部密度最大的点进行聚类,但仍需用户确定所需局部密度峰值点的个数,并未实现参数的完全自适应.
本文提出一种自适应局部半径的密度聚类算法SALE-DBSCAN(An Self-Adaptive LocalepsDBSCAN).该算法只需用户确定一个参数minPts,计算所有点的局部密度,自适应发现符合条件的局部密度峰值个数,并通过自适应选择eps扩张峰值点邻域,最后通过类标记合并实现聚类.实验结果表明SALE-DBSCAN算法能够对任意形状,且具有不同密度的数据集进行准确聚类.
本文后续的组织如下,第2节介绍密度聚类的相关概念,第3节介绍SALE-DBSCAN算法基本概念、思想与实现步骤,第4节通过实验对SALE-DBSCAN算法的聚类效果和性能进行分析,最后对分析总结了进一步可能的工作.
2 密度聚类相关概念
密度聚类算法的基本相关概念如下[1]:
eps邻域一个用户指定的参数eps>0用来指定每个对象的领域半径.对象o的eps领域是以o为中心,以eps为半径的空间.
邻域的密度由于邻域大小由参数eps确定,因此邻域的密度可以简单地由邻域内的对象数度量.用户指定一个参数minPts,作为稠密区域的密度阈值.
核心点对于指定对象p,如果p的eps邻域内所包含数据点的数量大于或等于minPts,则把对象p称为核心点.
直接密度可达给定一个点集合D,如果点p在点q的eps邻域内,而q是一个核心点,那么说从点q出发到点p是(关于eps和minPts)直接密度可达的(directly density-reachable).
密度可达如果存在一个点链p1,p2,…,pn,p1=q,pn=p,对于pi∈D(1≤i≤n),pi+1是从pi关于eps和minPts直接密度可达的,则点p是从点q关于eps和minPts密度可达的(density-reachable).
密度连通如果存在点o∈D使得点p和q都是从o关于eps和minPts密度可达的,那么点p到q是关于eps和minPts密度连通(density-connected)的.
噪声点不被包含在任何簇中的点被称为噪声点(noise).
3 SALE-DBSCAN算法
本文提出的SALE-DBSCAN算法基于如下假设,即数据集中数据点分布不均匀,聚类核心点拥有比它周围数据点更高的局部密度.可以通过计算所有数据点的局部密度,发现局部密度峰值点.通过计算局部密度峰值点所属簇的局部半径,再通过邻域扩张以及对初步发现的簇进行合并,即可达到聚类的目的.SALE-DBSCAN算法只需用户指定簇的最小点数,大大减少了参数选择的难度.同时该算法能自动发现各簇的局部半径,提高了聚类结果的准确率.SALE-DBSCAN算法的主要流程包括以下三个步骤.
1.发现密度峰值点;
2.扩张密度峰值点邻域;
3.合并初步聚类结果与冲突处理.
3.1 发现密度峰值点
聚类分析的基本要求是簇内对象的距离尽可能小、不同簇间对象的距离尽可能大.从基于密度的簇的定义来看,可以将簇看做是由低密度区域分隔开的高密度区域.由此可以推知密度峰值点具有两个典型特征,一是密度峰值点具有更高的局部密度;二是与其它簇间对象的距离比同簇中非密度峰值点与其它簇间对象的距离更大.计算每个数据点的这两个特征即可发现密度峰值点.
定义1.数据点的邻域 给定最小点数(minPts),数据点p的邻域Np定义为,距离p最近的minPts个数据点组成的集合.
定义2.数据点的局部密度 给定最小点数(minPts),数据点p的局部密度(ρp)定义为:
(1)
其中,Np为p的邻域,Dist(·)为距离函数,在本文中采用欧式距离.
为了度量密度峰值点与其它核心点的差异性,将数据点p的差异度量δp定义为:
(2)
即δp为所有比p点局部密度大的点到p点距离的最小值.当p的局部密度最大时,p最有可能是一个密度峰值点,此时δp定义为:
(3)
由p和δ的定义可知,密度峰值点的ρ值会尽可能的小,而δ值会尽可能的大.以Aggregation数据集为例,其初始数据分布如图1 (a)所示,当minPts取值为15时,其数据点在ρ-δ空间的分布情况如图1 (b)所示.由图1 (b)可以明显看出大部分数据点都集中在了一起,而越接近密度峰值点定义的点(离散点)与聚集点分离的越远.ρ-δ空间中离散点在原数据空间的分布情况如图1 (a)中的被圈出的点.
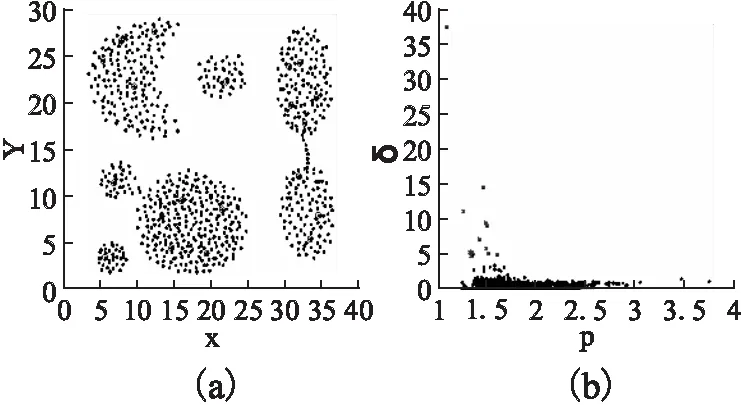
(a) Aggregation (b) 密度峰值点 数据集初始分布 选择决策图 (a)Aggregation dataset (b) Decision graph initial distribution for the data in (a)图1Fig.1
为了在ρ-δ空间自动发现密度峰值点,本文首先计算每个数据点的ρ与δ的比值γ,定义如下:
γp=δp/ρp
(4)
又根据ρ和δ的定义,数据点的γ值越大,表明该数据点越可能是密度峰值点.对Aggregation数据集中所有数据点的γ值

(a) 对γ从小到大排序 (b) 求(a)中γ的差值(a)Value of γ in increasing (b) Value of Δγorder for the data in Figure 1 图2Fig.2
从小到大排序,可以得到如图2 (a)所示分布.由于γ进一步放大了密度峰值点与其它数据点的差异,因此在图2 (a)中值剧烈变化的点可以考虑作为密度峰值点.本文通过计算γ的一阶差分,即Δγ=γi+1-γi,可显著地发现密度峰值点,如图2 (b)中的离散点.此时密度峰值点的选择条件为:
(5)
3.2 扩张密度峰值点邻域
采用上节所示的方法,在数据集中找到密度峰值点之后,即可通过扩张其邻域,以挖掘出该点所在簇.本文提出一种自动选择局部半径的邻域扩张算法,较好的解决了使用全局簇半径导致聚类结果不准确的问题.扩张密度峰值点邻域的具体步骤如下:
1)任取一个密度峰值点p,根据其自身的局部半径eps进行邻域查询,求出p的邻域Np,如算法1所示;
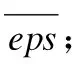

4)Np=Np∪N'p;
5)重复步骤2,直到Np不再变化;
SALE-DBSCAN算法在邻域扩张时会多次访问相同的数据点.为提升算法效率,可以为每个数据点设置访问标记,在扩张数据点邻域时,对已访问过的数据点在本次邻域扩张中不再重复访问,具体见算法2.
算法1.邻域查询算法
输入:数据集D,密度峰值点p,查询半径eps
输出:邻域点集Np
过程:
1:For eachiinDDo
2: IfDist(p,i)≤eps
3: PushiintoNp
4: End If
5:End For
6:ReturnNp
算法2.密度峰值点邻域扩张算法
输入:数据集D,密度峰值点集P
输出:簇集合C
过程:
1: For eachpinPDo
2: 初始化数组visited[|D|]=0
3: 对p进行邻域查询获得Np
4:visited[Np]=1

6:D=D-Dvisted=1
7: For eachiinNp
8: 对i进行邻域查询获得N'p
9:Np=Np∪N'p
10:visited[Np]=1
12:D=D-Dvisted=1
13: End For
14: End For
3.3 合并初步聚类结果与冲突处理
3.1节提出的密度峰值点发现方法,无法保证每个簇中只包含一个密度峰值点,如图1 (a)中所示.因此,在对每个密度峰值点进行邻域扩张后,需要将包含相同元素的簇进行合并.合并簇时,主要需要考虑两种情况:
1)两个密度峰值点在同一个簇中,如图3中所示的A和B点,此时可直接合并这两个密度峰值点所在的簇.
2)两个密度峰值点的簇有交集但不属于同一个簇,如图3中所示的C和D点.它们各自所在的簇有共同的交集(E点),但是C和D明显应该属于不同簇,此时不能直接将C、D所在簇合并.E点的隶属问题就是簇合并中的冲突问题.

图3 聚类合并情况示意图Fig.3 Dataset initial distribution in clusteR merging
为了解决此类冲突问题,本文提出了一个解决方案.在合并两个簇前,首先考察其交集中是否包含密度核心点,若包含密度核心点这说明这两个簇属于第一种情况,可以直接合并两个簇;若不包含任何密度核心点则属于第二种情况,此时需进一步确定其交集元素的隶属问题.以图3中的E点为例,假设左边的簇标签为1,右边的标签为2,E的隶属函数定义为:
(6)

4 实验与分析
本文采用Matlab编程实现了SALE-DBSCAN算法,并在不同形状、大小和密度分布的多个数据集上,通过实验对比了采用全局聚类半径的DBSCAN算法、使用了基于贪心策略选择的局部聚类半径的Greedy-DBSCAN算法与SALE-DBSCAN算法聚类结果和运行效率.实验结果表明,SALE-DBSCAN算法在聚类质量上优于DBSCAN算法和Greedy-DBSCAN算法.具体的实验结果与分析如下.
4.1 实验环境
实验的软硬件环境如下所示:
操作系统:Windows 10;
开发工具:Matlab 2016;
CPU:Inter Core i5-4200H 2.80GHz;
内存:8GB
4.2 实验结果分析
本实验中所使用数据集均取自Shape Sets[14].在不均匀数据集中,以compound数据集为例,DBSCAN算法把图4(a)中A区域点错误判定为噪声点(噪声点标识为“×”);Greedy-DBSCAN算法虽然使用了局部半径进行聚类,但是未能有效识别噪声点,如图4(b)中的B区域中形状不同的点.SALE-DBSCAN算法对compound数据集所有簇与噪声进行了准确划分,如图4(c).

图4 compound聚类结果图Fig.4 Compound dataset clustering result

图5 flame聚类结果Fig.5 Flame dataset clustering result
在相对均匀数据集中,以flame数据集为例,DBSCAN算法的聚类结果中出现了被错误划分的噪声,如图5(a)所示;Greedy-DBSCAN算法得到了相对准确的聚类结果,但是从图5(b)中的B区域可以看出,在簇的边缘区域出现了将原本应该归为簇中的点判定为噪声的情况(噪声用“□”表示);而SALE-DBSCAN算法的聚类结果将数据集比较精确的分为两个簇,同时降低了误判噪声的数量,在flame数据集上得到了优于其他算法的聚类结果,如图5(c).
为更进一步验证聚类结果的准确性,本文使用SALE-DBSCAN算法分别对Aggregation、R15和t4.8k数据集进行聚类.在球状数据集中,SALE-DBSCAN算法能够获得比较准确的聚类结果,如图6(a)、图6(b);在不规则且存在干扰点的数据集中,SALE-DBSCAN算法能够有效处理干扰点,如图6(c).
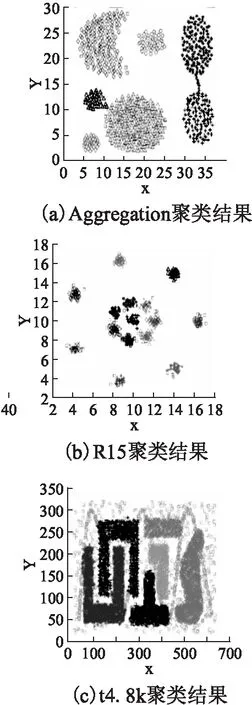
图6 SALE-DBSCAN聚类结果展示Fig.6 SALE-DBSCAN clustering result
在5个不同数据集中,采用F度量(F-Measure)[16]对聚类结果的准确度进行定量分析.结果显示SALE-DBSCAN算法的聚类精确度均高于DBSCAN算法与Greedy-DBSCAN算法,如图7所示.实验表明SALE-DBSCAN算法的聚类质量优于其他两种算法.但是,由于SALE-DBSCAN在参数自适应选择、聚类合并过程中产生了大量时间开销,因此时间消耗要高于其他两种聚类算法,具体对比结果如图8所示(三个准确率从左至有分别为SALE-DBSCAN、Greedy-DBSCAN、DBSCAN).
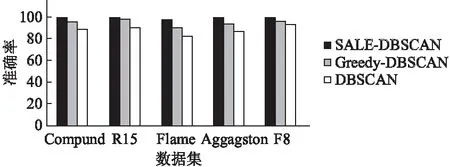
图7 聚类准确率对比图Fig.7 Clustering precision
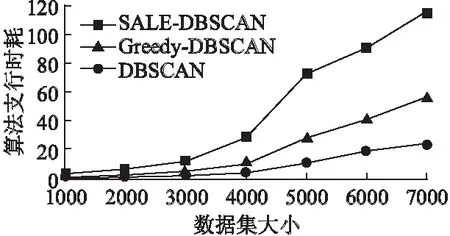
图8 运行时间对比图Fig.8 Running time
5 结 语
本文提出了一种自适应局部半径DBSCAN算法,该算法不但继承了密度聚类算法的优点,能够对任意形状的数据集进行准确聚类;并且仅需用户指定一个参数,实现了邻域半径选择的自适应;实验证明本文所提算法聚类结果明显优于DBSCAN算法与Greedy-DBSCAN算法;但由实验结果可知,目前SALE-DBSCAN算法时间效率要低于DBSCAN算法与Greedy-DBSCAN算法.下一步目标是如何将改进算法与MapReduce、网格技术相结合;通过网格技术对数据进行预处理,划分成多个数据块并保持数据间的密度可达性,通过MapReduce完成对海量数据的聚类.

