一种基于枢纽现象和加权离群分数的离群数据挖掘算法
郭 峰,张继福
(太原科技大学 计算机科学技术学院,太原 030024)
1 引 言
离群数据是指明显偏离其他数据,不满足数据的一般模式或行为,与存在的其他数据不一致的数据,或者明显偏离其它数据[1],已经广泛应用在天文光谱数据分析[2]、灾难天气预报[3,4]、金融[5]、网络入侵检测[6]等领域.由于"维度灾难"的影响[7,8],大多数在低维数据空间中表现良好的离群挖掘算法,在高维数据空间中效果变差,其主要原因是在高维数据空间中的数据变得稀疏,任意两个数据对象之间的距离趋于一致,隐藏了真实离群数据,使每个数据对象都几乎成为离群数据[9],因而大多数离群数据挖掘方法无法适用于高维数据集.
k近邻查询在离群数据挖掘中有着广泛的应用,枢纽现象(Hubness)是维度灾难中与k近邻查询相关的一个概念[10,11].枢纽现象是指在高维数据集中,任意数据对象i出现在其他数据对象k近邻列表中的次数Nk(i),其次数分布呈现明显的右偏态,一些数据对象(antihubs,称为非枢纽点)很少或者不出现在其他数据对象kNN列表中.随着数据维度的增大,枢纽现象越来越明显,且非枢纽点与高维数据集中的离群数据存在密切关联关系[12].本文针对高维数据集,利用枢纽现象给出了一种基于枢纽现象和加权离群分数的离群数据挖掘算法.该算法首先计算逆k近邻,得到每个数据对象的离群分数;其次使用每个数据对象与其k近邻点的距离,对其k近邻点的离群分数之和进行加权,获得加权k近邻分数和作为启发性条件,并且多次随机选择区分度比例计算每个数据对象的区分度,将所得区分度平均值设为区分度阈值,大于区分度阈值则认为所选取区分度比例是满意值;然后将每个数据对象的离群分数与其加权k近邻分数和,按区分度比例满意值求和,得到该对象的离群程度,选取离群程度最大的若干数据对象作为离群数据.最后采用人工数据集和UCI 标准数据集,实验验证了该算法的有效性.
2 相关工作
传统的离群数据挖掘方法,例如基于统计[13]、基于距离[14,15]、基于密度[16,17]、基于子空间[18,19]等,都会受到"维度灾难"的影响,在高维数据集中挖掘效果较差.k近邻查询是离群数据挖掘中的一种简单和基本步骤,影响着离群挖掘效果.
k近邻查询是指根据相似性度量在数据集中寻找或查询与给定对象最邻近的k个数据对象[20],并广泛应用在离群数据挖掘中,其典型研究成果为:Ramaswamy等人[14]首先提出基于k近邻的离群数据检测算法,计算数据集中每个数据对象与其第k近邻之间的欧氏距离,距离最大的n个数据对象是离群数据,其缺点是距离相同时的离群数据判断;Angiulli等人[15]将离群数据认为是与其k近邻距离之和越大的n个数据对象,并提出HilOut算法,其主要思想是利用空间填充曲线计算近似k近邻,找到候选离群数据准确计算进行筛选.Östermark[21]提出Fuzzy KNN算法,将模糊knn与遗传算法结合,在时间序列中进行离群数据挖掘.
逆k近邻查询是指给定一个查询数据对象,根据相似性度量返回一个结果集,该结果集中每一个数据对象都将该查询数据对象作为其k近邻[22].在逆k近邻查询中,查询数据对象与数据集中其他数据对象相似性相关,具有低逆k近邻值的数据对象很少或者不出现在数据集其他数据对象的k近邻列表中,与离群数据存在关联关系[12].逆k近邻查询广泛应用在在离群数据挖掘中,典型研究成果为:Hautamaki等人[23]提出了ODIN算法,该算法将任意一个数据对象i出现在其他数据对象k近邻列表中的次数Nk(i)分数被认为是该数据对象的离群分数,并分析了为何Nk(i)分数能够构成有意义的离群分数的原因,其缺点是需要人为设定离群分数阈值,不适应于未知数据分布的离群数据挖掘;Lin等人[24]提出了一种ODIN算法的变体,遍历数据集中所有数据对象,将离群数据认为是Nk(i)=0的数据对象,其缺点是离群挖掘结果受数据分布影响,包含在小簇中的离群数据可能被隐藏.
枢纽现象是"维度灾难"与逆k近邻查询相关的一个概念,并随着数据维度的增大,枢纽现象越来越明显.Radovanovic等人[12]首先分析了枢纽现象,并表明在低维和高维数据中,非枢纽点和离群数据均存在关联关系;随着空间维度的增大,枢纽现象使数据集产生更显著的枢纽点和非枢纽点,并据此提出了适用于高维离群检测的AntiHub算法和AntiHub2算法.AntiHub算法计算数据集中每个数据对象的Nk(i)值,根据Nk(i)值计算离群分数.AntiHub2算法在AntiHub算法的基础上引入启发性信息,在计算一个数据对象的离群程度时除了考虑该数据对象的Nk(i)分数还考虑其k近邻数据对象的Nk分数和,设置step参数进行遍历,找到最大区分度比例α,将当前数据对象的Nk(i)分数与其k近邻数据对象的Nk分数和按最大区分度比例α求和,得到离群程度,选取离群程度最大的若干数据对象作为离群数据.
综上所述,现有的基于逆k近邻(RkNN)的离群挖掘算法均使用Nk(i)值,对Nk(i)值操作得到离群分数.ODIN算法和AntiHub算法对离群数据和正常数据对象的区分度不高,主要原因是Nk(i)本质上是离散的,较大的k值选择提高区分度但运算代价昂贵.AntiHub2算法能够在较小的k值选择下获得较高的区分度,其缺点是计算过程中需要设置参数进行遍历,时间复杂度高,同时也都没有考虑距离因素.
3 枢纽现在与相关概念
3.1 枢纽现象
枢纽现象(Hubness)是指高维数据空间中,任意数据对象i出现在其他数据对象k近邻列表中的次数Nk(i)的分布呈现出明显的右偏态,且右偏程度会随着数据维度的增加而增大,导致少量的枢纽点(hubs)非常频繁地出现在数据集其他数据对象的kNN列表中.而另外一些非枢纽点(antihubs)很少或者不出现在数据集其他数据对象的kNN列表中.参照文献[10]右偏程度的计算公式定义如下;
(1)
其中:μNk和δNk分别表示Nk(i)的均值和标准差.当SNk>0 时,SNk值越大,Nk(i)的右偏程度就越高,数据集的枢纽现象就越明显.
枢纽现象与"维度灾难"相关.当高维数据出现"维度灾难"时,任意两个数据对象之间的距离趋于一致,反映相似性差异的各种距离指标效果变差,大部分数据对象将落在以数据质心为中心的超球体表面上[10].该特征使得显著低于超球体表面的数据对象更有可能出现在其他数据对象的kNN列表中,即这些数据对象具有更高的Nk(i)值,被称为枢纽点.与此对应,显著远离超球体表面的数据对象很少或者不出现在其他数据对象的kNN列表中,具有较低的Nk(i)值,被称为非枢纽点.超球体表面附近的数据对象,即"规则"数据对象,倾向于具有接近k的Nk(i)期望.若数据集来自多个分布,那么大部分数据点将落在以相应分布的质心为中心的超球面上.
3.2 相关概念
在文献[12]中,将给定数据对象i的Nk(i)值归一化,并计算其离群分数,计算公式定义如下:
(2)
其中:ai为数据对象i的离群分数.当Nk(i)=0时,由公式(2)也可使得数据对象i获得有意义的离群分数.计算每个数据对象的离群分数,选取离群分数最高的若干个数据对象,并将其视为离群数据.
在文献[12]中,引入启发性信息,在计算数据对象i的离群程度时,除了考虑其Nk(i)分数还考虑其k近邻数据对象的Nk分数和.k近邻Nk分数和(anni)的计算公式定义如下:
anni=∑j∈NN(k,i)aj
(3)
其中:anni为数据对象i的k近邻Nk分数和,数据对象j为其k近邻,aj为数据对象j的Nk(j)分数.数据对象i的离群程度计算公式定义如下:
cti=(1-α)·ai+α·anni
(4)
其中:cti为数据对象i的离群程度,ai为其Nk(i)分数,anni为其k近邻Nk分数和,α为最大区分度比例.计算每个数据对象的离群程度,选取离群程度最大的若干数据对象作为离群数据.
4 距离信息加权与区分度满意值
4.1 距离信息加权
指根据文献[15],离群数据是全体数据对象中与其k近邻平均距离最大的n个数据对象.现有的基于逆k近邻的离群挖掘算法都未考虑距离因素,因此引入距离信息作为权值,提高其准确率.k近邻距离定义为:给定数据对象与其k近邻数据对象之间欧氏距离的平均值.k近邻权值定义为:给定数据对象的k近邻距离与数据集k近邻距离平均值的比值,其计算公式定义如下:
(5)
其中:wi为数据对象i的k近邻权值,averDisk(i)为其k近邻距离,averDisk为数据集k近邻距离平均值.
根据公式(2)(3),计算数据对象i的归一化Nk(i)分数ai和其k近邻Nk分数和anni.ai值较高的数据对象Nk(i)值较低,较少或者不出现在数据集其他数据的k近邻列表中,并与离群数据存在关联关系,因此可以使用ai计算离群分数.因为ai在本质上离散,对离群数据与正常数据区分度低,引入anni作为启发性条件能够提高算法区分度.对于给定数据对象i,使用其k距离权值对其k近邻Nk分数和anni进行加权,得到加权k近邻Nk分数和(Wanni),其计算公式定义如下:
Wanni=anni·wi
(6)
其中:Wanni为数据对象i加权k近邻Nk分数和,anni为其k近邻Nk分数和,wi为其k近邻权值.参照文献[12],离群程度计算公式可重新定义为:
cti=(1-α′)·ai+α′·Wanni
(7)
其中:cti为数据对象i的离群程度,ai为其Nk(i)分数,Wanni为其加权k近邻Nk分数和,α′为区分度比例满意值.
当数据对象i为离群数据时,数据对象i的k近邻距离大于数据集k近邻距离平均值,其k近邻权值wi>1,所对应加权k近邻Nk分数和Wanni大于k近邻Nk分数和anni.根据公式(4)(7),对于离群数据,使用加权k近邻Nk分数和可获得比文献[12]高的离群分数,提高正常数据对象和离群数据的区分度.利用信息作对离群分数进行加权还具有以下优点:当数据集不满足任何特定分布模型时,距离信息仍能有效地发现离群数据;k近邻查询,可获得所有数据对象的k近邻距离,不需要进行额外计算.
4.2 区分度满意值

使用区分度阈值分支判断可以有效减少循环次数,提高算法效率.为适用于数据分布未知的数据集,自动生成区分度阈,根据区分度阈值判断区分度比例满意值,并根据公式(7)使用区分度比例满意值计算离群程度.自动生成区分度阈值用于分支判断,使用区分度比例满意解α′计算离群程度的步骤如下:
从α′∈(0,step,2·step,…,1)中多次随机选取α′,每个α^′值调用局部函数discScore(y,ρ)计算对应区分度,多次实验所获得区分度平均值设为区分度阈值Threshold;继续从α′∈(0,step,2·step,…,1) 中多次随机选取α′,如果所选取α′对应区分度大于区分度阈值,则认为所选取α′为一个区分度比例满意值;使用区分度比例满意值α′计算离群程度.
计算区分度满意值α′的过程是在所有α取值中随机选取有限个α′,根据区分度阈值判断是否为区分度比例满意值α′.当搜索参数step设置较小时,使用区分度满意值α′可以减少算法循环次数.在计算区分度比例满意值α′的过程中,采用随机抽样,计算得到的区分度比例满意值α′具有随机性,因此m次随机选择α′,计算区分度比例直到获得n个区分度比例满意值.
5 离群数据挖掘算法描述
综上所述,引入距离信息对离群分数加权提高离群数据与正常数据的区分度,提高离群数据挖掘效果;使用区分度满意值分支判断减少循环次数,提高了离群数据挖掘效率.利用距离信息和区分度比例满意值,计算离群程度的基本步骤:首先对数据集中的每个数据对象进行逆k近邻查询,得到每个数据对象出现在其他数据对象k近邻列表中的次数Nk,根据公式(2)、(3)计算数据对象i的Nk(i)分数与其k近邻Nk分数和;其次使用每个数据对象的k近邻权值对其k近邻Nk分数和加权,得到加权k近邻Nk分数和;然后多次随机选择α′值计算其区分度,将所得区分度平均值设为区分度阈值,大于区分度阈值则认为所选取α′是满意值;最后使用公式(7)计算每个数据对象的离群程度,选取离群程度最高的若干个数据对象,并将其视为离群数据.其算法描述如下:
算法:WAntiHub(Weighted Anti-Hubness for Unsupervised Distance-Based Outlier Detection)
输入:数据集D中每个数据的k近邻;采样比例ρ∈(0,1];搜索参数step∈(0,1]
输出:离群数据
1)n=数据集D的数据个数;
2)for(i=0;i 3) 根据公式(2)计算数据对象i的归一化Nk(i)分数ai; 4) 使用ai,根据公式(3)计算数据对象i的k近邻Nk分数和anni; 5) 根据公式(5)计算数据对象i的k近邻权值wi; 6) 使用wi和anni,根据公式(6)计算数据对象i的加权加权k近邻Nk分数和Wanni; 7)end for; 8)α从(0,step,2·step,…,1)中随机取值,得到α1…αm; 9)for(j=0;j 10) for(i=0;i 11) 根据公式(7),使用α1…αm计算数据对象i的离群程度cti; 12) end for; 13) cdiscj=discScore(cti, ρ);//调用局部函数计算α1…αm对应区分度 14)end for; 15)Threshold=(∑1jcdiscj)/m ; //计算区分度阈值Threshold 16)α′从(0,step,2·step,…,1)中随机取值,得到α1′…αq′; 17)for(j=0;j 18) for(i=0;i 19) 根据公式(7)使用α′计算数据对象i的离群程度cti; 20) end for; 21) cdisc=discScore(cti, ρ);//调用局部函数计算α′对应区分度 22) if cdisc> Threshold;//根据阈值判断区分度比例满意值α′ 23) 记录所对应的区分度比例满意值α′; 24) if 已经保存了s个α′; 25) end if; 26)end for; 28)for(i=0;i 29) 根据公式(7)使用区分度比例满意值α^′计算离群程度 30)end for; 31)End WAntiHub 算法步骤说明: 1)局部函数:discScore(y,ρ):对于y∈Rn和ρ∈(0,1],根据采样比例找到y中值最小的「nρ⎤个值,进行去重操作,将非重元素个数除以「nρ⎤作为输出. 2)在上述算法中2)-7)计算数据集中每个数据对象Nk(i)归一化分数ai,使用k近邻权值对其k近邻Nk分数和进行加权,得到加权k近邻分数和Wanni.8)-15)多次随机选择α值计算区分度阈值Threshold.16)-27)多次随机选择α′,使用区分度阈值判断,获得区分度比例满意值α′.28)-30)使用区分度比例满意值α′计算每个数据对象的离群程度,选取离群程度最高的若干个数据对象,并将其视为离群数据. 算法复杂性分析: 实验环境:Inter Core(TM) i7-6700HQ CPU 16GB内存,windows 10操作系统,eclipse作为开发平台,采用Java语言实现了WAntiHub算法和AntiHub2算法[12].实验数据包括人工数据集和UCI数据集. 人工数据采用随机生成正态数据,并将数据集中的1%元素乘以1.5倍作为离群数据. 1)近邻数k 图1 近邻数k对算法的影响Fig.1 Influence of the neighbor number k on the algorithm 由图1(b)表明随着k值的增大,WAntiHub算法耗时呈现线性增长.主要原因是Wantihub算法和Antihub2算法都使用(加权)k近邻Nk分数和,k值越大,计算(加权)k近邻Nk分数和的数据也随之增多.对所有的k值,WantiHub算法的效率高于AntiHub2算法,主要原因是WAntiHub算法使用区分度比例满意值α′代替最大区分度比例α用于计算离群程度,分支判断减少了循环次数. 2)数据量 图2是采用100维数据的实验结果,由图2(a)表明随着数据量的增大,WAntiHub算法的准确度基本不变,AntiHub2算法的准确度有缓慢的提高.主要原因是数据量的增加使数据更加聚集,枢纽现象程度加深,非枢纽点更加显著.对所有数据量,WAntiHub算法的准确度高于AntiHub2算法. 图2 数据量对算法的影响Fig.2 Influence of the amount on the algorithm 由图2(b)表明随着数据量的增大,WantiHub算法耗时呈指数型增长.主要原因是WantiHub算法的时间复杂度为O(n2·t).对所有的数据量,WAntiHub算法的效率高于AntiHub2算法. 3)属性维度 图3是采用10000条数据,k=100的实验结果.由图3(a)表明随着属性维度的增大,WAntiHub2算法和AntiHub2算法的准确率提升.主要原因是数据属性维度增大使枢纽现象程度加深,非枢纽点更加显著.AntiHub2算法对准确率的提升高于WAntiHub算法,其主要原因是属性维度增大使数据集中任意两个数据对象之间的距离趋于一致,使基于距离信息加权的效果变差.对所有的属性维度,WantiHub算法的准确率高于AntiHub2算法. 图3 属性维度对算法的影响Fig.3 Influence of the dimension on the algorithm 由图3(b)表明对所有的属性维度,WatiHub算法运算时间基本一致.主要原因是WantiHub算法使用k近邻查询结果作为输入数据,对属性维度不同的数据集,其k近邻查询结果所包含的数据量基本一致.对所有的维度,WAntiHub算法的效率高于AntiHub2算法. 4)采样比例ρ 图4是采用10000条100维数据,k=100的实验结果.由图4(a)表明采样比例ρ对WAntiHub算法精确度影响较小.且对所有的ρ值,WAntiHub算法的准确率高于AntiHub2算法. 图4 采样比例ρ对算法的影响Fig.4 Influence of the sampling ratio on the algorithm 使用UCI数据集Yeast,HTRU2,Ionosphere,ESRDS验证算法准确率和效率,所有UCI数据都转化为标准分数. 表1 UCI数据集信息Table 1 UCI dataset information 图5 UCI数据集对算准确率的影响Fig.5 Influence of algorithm accuracy on the UCI dataset 由图5表明在所有UCI数据集上,WAntiHub算法的准确率高于AntiHub2算法,WAntiHub算法对低维数据集Yeast、HTRU_2和中维数据集HTRU_2准确率提高较多,对高维数据集ESRDS准确度提升较小.主要原因是随着属性维度的增大,使用距离信息加权的效果变差. 由图6(a)表明,WantiHub算法对Yeast和Ionosphere数据集效率提升较大,主要原因是Yeast和Ionosphere数据集数据量较小,遍历找到最大区分度比例α占总运算时间比例大,使用区分度阈值分支判断有效减少循环次数.图6(b)显示对HTRU_2和ESRDS数据集,效率提升较小.主要原因是数据集数据量较大,计算每个数据对象的Nk(i)值占总运算时间比例大.在所有UCI数据集上,WAntiHub算法效率提高. 针对高维数据中维度灾难导致离群数据挖掘效果变差,利用逆k近邻中出现的枢纽现象,给出了一种基于枢纽现象和加权离群分数的离群数据挖掘算法WAntiHub.该算法引入距离信息对离群分数加权,提高离群数据挖掘效果;使用区分度满意值分支判断减少循环次数,提高了离群数据挖掘效率.使用人工数据和 UCI 数据集,实验验证了该算法的有效性.为适应海量数据的需求,WAntiHub算法的并行化将是下一步的研究工作. 图6 UCI数据集对算法效率的影响Fig.6 Influence of algorithm efficiency on the UCI dataset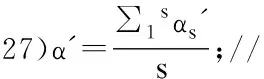
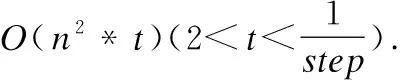
6 实验结果及分析
6.1 人工数据集
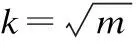





6.2 UCI数据集


7 结束语