井下地磁定位的匹配算法分析和优化*

郭云飞,汪金花,吴 兵,张 博,高 伟

(华北理工大学矿业工程学院,河北 唐山 063210)

地磁定位技术是将采集的实时地磁数据与地磁基准图按照某种匹配算法进行搜索匹配,根据匹配度量确定最佳匹配位置的技术。地磁定位在卫星、无人机、舰艇导航应用成熟,主要完成导航过程中的地磁辅助定位,或者与惯导系统进行组合定位。其中地磁数据采集、地磁基准图构建、匹配算法选取是地磁定位结果的重要影响因素,匹配算法优劣直接决定了导航精准度。国内外关于地磁匹配算法与精度已经进行系统深入研究,取得了一些代表性成果。谢仕民等在地磁匹配导航关键技术浅析中对地磁匹配导航研究的由来以及发展等现状做了简要的介绍以及其未来的展望[1];随后,谢仕民等又在大范围的区域进行仿真实验对比分析了各匹配算法的优劣性[2];李鑫等在对水下地磁导航的研究过程中,利用磁总场的梯度作为特征量进行了地磁匹配的仿真实验验证了其优势以及可行性,改进后的算法定位比经典MSD算法提高了26.17%[3];肖晶等通过对匹配算法的理论进行分析对比的同时为地磁导航算法提出了改进的新策略[4];李明明等在对地磁导航的研究中为了提供航空器的运动学状态提出了利用UPKHNA进行地磁导航,仿真结果表明其导航结果可以较好地估计SINS的导航误差,水平定位性能优于仅使用UPF的导航误差[5];郭庆等运用仿真实验对所提出的双等值线匹配算法的有效性进行了验证[6]。王闯等对二维最小绝对差累加和算法的地磁匹配导航方法进行了分析和验证,证明该方法在一定情况下动态匹配效果较好[7]。Wang E等提出了使用中值滤波算法处理磁场数据弥补室内定位算法的不足之处[8]。Zhong Guosong等在地磁辅助导航中运用矢量匹配法使其匹配概率和定位精度得到了较大的提高,文章提出了矢量迭代最近轮廓点(VICCP)算法对惯导系统(INS)的定位误差特性具有较好的适应性[9]。这些研究主要针对大区域地磁匹配算法分析与适用性评价,关于小区域内磁场匹配模型系统研究较少。由于地磁定位民用化刚刚起步,部分学者开展了小区域地磁定位试验,集中表现在室内地磁精度分析试验、地下车场地磁与视频组合的智能导航试验,关于井下地磁定位技术与匹配算法的分析鲜见报导。文中以井下地磁与射频组合定位技术为试验对象,进行了小区域带状地磁定位的匹配算法的精度分析试验,为井下地磁定位导航提供研究基础。

1 井下地磁匹配定位

1.1 井下地磁匹配

井下地磁定位技术是在无源射频定位的基础上,结合地磁定位实现井下人员定位的一种方法。包含射频识别初步定位和地磁匹配精确定位两个步骤,如图1所示。

井下地磁精确定位是依据行走路线地磁实时向量与区域地磁基准图进行定位匹配运算来实现。在井下有电且网络正常时,地磁定位位置信息可以通过井下通讯基站发送井下定位系统监控中心,实现信息共享。当井下发生突发状况或灾害,井下通讯网络发生供电中止或信号中断(不稳定)情况对井下地磁定位进行单独自主定位和实现避险导航。地磁导航的关键技术在于导航区域地磁数据库的建立,载体磁力仪的实时测量以及地磁匹配算法,其中地磁匹配算法是地磁匹配导航的核心技术,匹配算法的精度是决定导航精度的主要因素,是决定匹配导航过程中降低出现误匹配概率的重要因子[10-11]。

图1 井下地磁匹配定位流程图

1.2 匹配算法

匹配算法主要有相关度量匹配和递推滤波匹配,递推滤波常常受到滤波模型的限制,对初始误差要求较高,而且各种误差统计模型不易获取,滤波的发散也不易控制;相关度量法原理简单可以持续使用,因此文中选择对相关度量法进行研究。相关度量算法目前分为两类:一类是强调他们之间的相似程度,另一类是强调他们之间的差别程度[12]。

本文从两类算法中各取两种可行且具有代表性的算法进行研究,分别是互相关匹配(COR)、归一化互相关匹配算法(NCOR)、平均绝对差匹配(MAD)、均方差匹配(MSD)。这4种匹配算法因其原理的差异性,匹配算法的适用性及其优缺点各有不同,如表1所示。COR、NCOR、MAD、MSD算法已经广泛应用于图像匹配领域,算法稳定。

表1 4种常用的匹配算法对比

2 井下地磁匹配的适配性

2.1 地磁特征指标

井下地磁匹配属于线矢量与带状基准图之间的数字相关匹配,对区域地磁特征丰富性要求较高。待匹配区域地磁的分布特征的评价,是能否有效开展精确地磁导航的基础。在定位匹配区域中,地磁图不同空间坐标点的地磁值会出现相近或相同现象,空间坐标与地磁值不完全是一一对应的关系。地磁图适配性是地磁定位匹配的适应性,即地磁场特征在相关匹配中表征地理空间位置的能力。从公开文献来看,描述地磁图特征有地磁场均值、标准差、粗糙度、地磁熵、峰态系数、累加梯度均值等多达十几种[13-14]。文中根据井下地磁场表现特征选取了4种:平均地磁场、地磁标准差、地磁熵和地磁粗糙度,表2是井下地磁分布特征指标,根据指标数值特征可以量化评价区域地磁特征明显程度,确定待匹配区域适配性能的优良。

表2 井下地磁图适配性评价指标

2.2 适配性评价

地磁场是地球的基本物理场,处在地球近地空间内任意一点的磁场强度都会因为所处的经纬度以及高度不同而不同[15]。试验选取了唐山井下同一水平的三条长为150 m左右,宽度为6 m左右的水平巷道,使用FVM-400磁通门磁力仪对其进行磁总场的数据的采集。试验尽量避免外界干扰以及日变等影响,整个数据采集过程均在无磁暴等外界磁干扰的时段进行。井下结构复杂,巷道之间相互交叉或关联贯通的特性,实际的数据采集过程中按照需要注意科学的设计其采点格网密度[16]。最后对采样数据进行去噪以及空间插值等处理得到如图2所示的三条巷道地磁基准图。

图2 井下巷道地磁基准图

由图2可得,三条巷道的地磁基准图均具有一定范围的波动性,但是其波动变化又有一定的差别。巷道H-1的总磁场波动范围为50 000 nT到 55 000 nT,整体波动比较均匀;巷道H-2的总磁场波动变化为20 000 nT到80 000 nT,整体变化特征明显;巷道H-3的整体波动范围为48 000 nT到 64 000 nT,局部变化较明显。直观的对比可以看出H-2更加适合单独运用地磁信息进行匹配定位,H-3 巷道次之,H-1最不适合。在巷道基准图的基础上需对其进行适配指标分析,判断H-2是否是最适合单独进行地磁匹配,如表3所示为三条巷道的适配性指数。

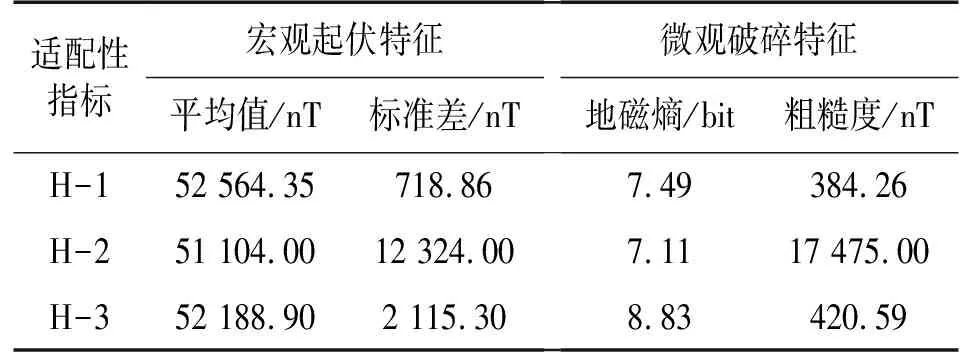
表3 巷道适配指数表

通过对表3的适配指标对比可发现在这三条巷道中H-2巷道的标准差最大,地磁熵最小,地磁粗糙度最大。综合判断可得巷道H-2是最适合单独利用地磁信息进行匹配定位的。H-3巷道虽然各项指标不如H-2巷道,但也相对较好。H-1巷道的适配性指标显示该巷道最不适合单独用地磁信息进行匹配定位,但在后续的研究中可以加入RFID射频或者其他磁标进行辅助定位最终满足导航需求。

3 区域地磁匹配

3.1 匹配算法对比

根据对三条巷道的定性以及定量的分析研究判断得到巷道H-2最适合单独进行地磁匹配算法研究。为了研究井下地磁定位匹配算法优劣和抗噪性能,巷道H-2地磁数据为试验原始基准,进行两种方式的处理。一是选取基准图的原始数据进行匹配研究对比;二是在选取的数据上添加一定量的噪声干扰进行匹配仿真对比。在不加噪的情况下,COR算法的匹配精度太低,出现虚定位现象。NCOR、MAD、MSD算法的误差都是零,说明这3种匹配算法在地磁匹配的应用中无原理性的错误,适合进行继续研究。

为了从匹配精度、匹配速度和鲁棒性三方面综合对比NCOR、MAD、MSD算法,将H-2地磁数据加入不同等级的噪声进行仿真试验。根据FVM 400磁通门磁力仪最大测量噪声100 nT,分别进行20 nT,50 nT和100 nT 3个等级的加噪匹配试验。图3为存在20 nT、50 nT以及100 nT干扰噪声情况下的匹配误差图。

图3 噪声对匹配结果的影响对比图

由图3可以看出,加噪20 nT时,MSD匹配算法和MAD匹配算法的匹配结果基本一致,均只出现了一次误匹配,NCOR匹配算法则实现了无误差匹配;加噪50 nT时,MSD匹配算法和MAD匹配算法出现了四到五次的误匹配现象,NCOR只出现了两次的误匹配;加噪100 nT时,MSD匹配和MAD匹配算法匹配结果出现了多次误匹配,NCOR匹配结果依然较好,没有太多的虚定位现象发生。虽然随着噪声的增加,匹配准确度越来越低,但就其匹配误差对比图来说,NCOR匹配算法的匹配结果最好,而MSD匹配算法优于MAD匹配算法。在其图像分析的基础上需对匹配结果进行定量分析对比其匹配性能,匹配算法的匹配性能主要包括匹配速度、匹配误差统计值和匹配概率3个方面,如表4所示为不同噪声等级下匹配结果对比表。

根据表4的匹配结果分析可得,随着噪声的增加,3种匹配算法同时出现了匹配速度降低,匹配误差变大,匹配概率变小的现象。综合对比来说NCOR匹配算法的抗噪能力最强,其次是MSD匹配算法,MAD匹配算法的匹配效果最差。但是NCOR匹配算法的计算量太大,匹配时间相对来说过长,不适用于较大区域的匹配研究,因此MSD匹配算法更为适合继续研究,考虑在其基础上进行改进以实现更加快速高精的匹配结果。

表4 噪声对匹配算法的影响结果对比表

3.2 MSD匹配算法改进

地磁测量易受干扰,实时测量地磁数值包含了时域磁扰动以及环境磁扰动等数值扰动。相邻点磁总场做了差值运算后,时域变化磁数值扰动影响大部分被相互抵消,残余部分影响变得很小,甚至只有几个纳特波动干扰。因此在提高导航定位的精度在对MSD匹配算法进行改进过程中考虑对磁总场进行相邻点位做差运算后再进行匹配,如下式:

将改进后的MSD匹配算法与原始匹配结果进行对比如图4所示。

图4 MSD与MSD(P)匹配结果对比图

由图4图像可得,在不同等级噪声下的MSD和MSD(P)匹配算法匹配结果对比可以发现,改进后的MSD匹配算法的匹配结果明显优于原始的MSD匹配算法,误匹配现象大大减少。对其匹配效果进行定量分析如表5所示。

表5结果显示MSD(P)匹配结果随着噪声的增加出现误匹配概率也不断增加,但其整体的匹配误差以及误差均方差和匹配概率都远优于MSD匹配算法,而且两者的匹配速度大致相当,因此MSD(P)匹配算法更加适用于井下区域地磁匹配。

表5 MSD与MSD(P)匹配结果对比表

4 总结

为了研究井下地磁定位匹配算法优劣和抗噪性能,以井下地磁与射频组合定位自主导航系统为基础,进行了井下同一水平下的小区域带状地磁定位的匹配算法的精度分析试验,得出以下结论:

①在MSD、MAD以及NCOR 3种加噪的地磁匹配中,3种方法均出现不同程度虚定位。从定位精度对比,NCOR>MSD>MAD;从匹配定位的耗时比校,NCOR用时远远大于MSD、MAD两种方法,综合匹配精度与速度分析,MSD算法符合较大范围的井下地磁定位的需要。

②为了减弱时域磁扰动以及环境磁扰动对匹配精度影响,对相邻点位的磁总场做差运算,优化了MSD算法。通过MSD和MSD(P)算法对比试验,MSD和MSD(P)算法随着噪声增大,虚匹配概率均不断增加,但MSD(P)算法匹配精度和鲁棒性明显优于MSD算法。

地磁测量过程易受干扰,实测的地磁往往会受到很多如模型误差、日变影响、随机误差等误差的影响。优化的MSD匹配算法适用于特征明显的区域匹配定位,能够消除部分常值干扰对匹配结果影响。对于实测序列随机噪声扰动,或者磁特征变化相似度较高的区域,还需要开展新的匹配算法研究或多维地磁向量匹配的研究。