MEMS穿孔板微执行器动态Pull-in特性分析*

季莅莅,方玉明,孜乃提古丽·布尔汉,戚 举,艾昕晨

(南京邮电大学电子与光学工程学院、微电子学院,南京 210023)

微执行器是MEMS的核心部分,它既可以为微系统提供动力,也可以成为微系统的操作和执行单元,其中静电驱动的微执行器是应用最广泛的执行器之一。在静电驱动MEMS执行器中,Pull-in现象是一个重要的影响因素,它限制了执行器的行程范围,Pull-in现象[1-9]包括静态和动态两种。

在实际的应用中,有些器件需要避免Pull-in现象,例如压力传感器[10]必须预防Pull-in现象的发生,因为两个板之间的吸合会导致短路,使器件无法继续操作。但是,在有些应用中,Pull-in现象也可以被加以利用,例如在MEMS开关[5]中,将驱动电压调至Pull-in电压附近,可以利用Pull-in现象关闭开关,从而降低了输入电压。通常,在MEMS的设计中,为了加速释放或者减小阻尼,会在平板上加工释放孔或叫做阻尼孔[11],从而减小压膜阻尼的影响。例如,在RF MEMS开关中,会采用具有刻蚀孔的穿孔结构来作为开关的释放膜,而利于膜的释放,减少驱动过程中的阻尼[12]。

MEMS执行器中的Pull-in现象一直是人们的研究热点。Farokhi H[2]等人利用Meijs-Fokkema公式建模,研究了考虑边缘场效应下,MEMS静电谐振器的动力学行为;Koochi A[3]等人基于Gurtin-Murdoch的表面弹性原理,研究了表面能对纳米桥的静态和动态Pull-in参数的影响;Liao L D[4]等人以五阶泰勒级数展开的封闭解预测Pull-in参数,研究执行器规格和压膜阻尼效应对圆形板电容式执行器Pull-in现象的影响,发现可动板厚度的变化会改变压膜阻尼效应对Pull-in电压值的影响。并且,Harsha C S[6]等人研究了压膜阻尼对于静电驱动微开关的影响,利用压膜阻尼可以增大Pull-in电压并使系统在动态环境下更稳定。Liu J[7]指出当上电极宽度增大或者上下电极之间间距减小到一定程度时,阻尼作用力甚至可以与驱动的静电力达到同一数量级。

如今,有关穿孔板的静态Pull-in参数已经有了较为详细研究成果[1],因此本文主要基于穿孔板的结构,介绍静电驱动原理和Pull-in现象,并通过能量法进行理论分析,将理论计算结果与仿真结果进行对比,探究不同阻尼比下,微执行器的动态Pull-in现象,得到阻尼大小对Pull-in参数的影响。

1 静电驱动原理及结构简化模型

1.1 静电驱动原理

两端固支的穿孔板微执行器结构如图1所示。可动板中间带孔结构为上电极,不可变形的固定板为下电极,支撑结构的四根腿长Lleg,宽Wleg。当在上下驱动电极之间施加驱动电压时,在静电力的作用下,固支梁产生变形向下挠曲[8],随着电压增大,梁的挠度增加,当电压超过临界电压时,上电极会被吸合到下电极上,从而发生Pull-in现象。

图1 两端固支穿孔板静电微执行器结构

1.2 结构简化模型

当对穿孔板微执行器结构进行动态性能分析时,可以将静电驱动梁假设为弹簧谐振系统,如图2所示。B板为固定板,A板为可动板,板间间距为g0。穿孔板的长为l、宽为w、高为h,穿孔的形状为边长为a的正方形,且孔边缘与孔边缘的间距为d,孔边缘与板边缘的间距为r。

图2 穿孔板静电微执行器简化模型

该系统为阻尼机械系统模型,B板固定,A板与弹簧相连。A板受静电力和弹簧回复力共同作用,只能上下垂直移动。

在静态分析系统中,忽略惯性和阻尼的作用,可动板不会产生振荡。在两极板之间施加固定电压值,在电场力作用下,可动板向下移动,两极板间距变小,弹簧形变,可动板同时受到弹簧回复力,系统在电场力和弹簧回复力的作用下,达到平衡,极板也处于静止状态。当电压增加到一定值时,极板会移动到一个临界的平衡位置,此时,若继续增加电压或者给系统一个微小的扰动,系统失稳,可动板立刻吸合到固定板。对应的临界点即为静态Pull-in点,此时的电压为静态Pull-in电压[9]。

在动态分析系统中,在两极板之间施加阶跃电压信号,能量瞬间注入系统,可动板发生位移并且在第一个周期移动到最大位移。由于惯性的存在,如果未到达Pull-in点,可动板将做周期性的等幅振荡运动(忽略阻尼)或衰减的周期振荡运动(考虑阻尼);若到达Pull-in位置,可动板到达最大位移处将立即吸合到固定板。

2 理论分析

静电微执行器在加载阶跃电压信号后,要发生Pull-in现象,需要一定量的能量瞬间注入到系统中,下面利用机械系统的能量存储和转换,采用“能量法”,利用整个系统的能量变化来研究穿孔板静电微执行器在施加阶跃电压信号后Pull-in特性。

阶跃电压信号的表达式为:

v(t)=V0U(t)

(1)

式中:U(t)为单位阶跃函数,V0为幅值,图3为阶跃电压信号,下文中涉及的施加电压值均指阶跃电压的幅值。

图3 阶跃电压信号

在施加电压前,整个系统处于静止状态,施加电压后,系统瞬间被注入能量,可动板发生运动产生动能,同时弹簧发生形变产生弹性势能,并且伴随着可动板的运动会产生阻尼消耗。因此,整个系统的能量表达式[4]为:

Ein=Ekine+Epoten+Edamp

(2)

式中:Ein为注入系统的能量,Ekine为系统的动能,Epoten为系统的势能,Edamp为阻尼消耗的能量。加载阶跃电压信号后,可动板发生运动,产生位移,此时可动板受到垂直向下的静电引力Felec和垂直向上的弹性力Felas。

(3)

Felas=kx

(4)

式中:x为可动板的位移,g0为两极板的初始间距,ε为介电常数,A为两极板的正对面积,V0为阶跃电压的幅值,k为等效的弹簧弹性系数。

2.1 忽略阻尼的理论计算

在真空中,阻尼很小,可以忽略不计,即Edamp=0。且当可动板到达最大位移时,所有能量转化为弹性势能,则Ekine=0,因此式(2)转化为:

(5)

进行积分处理,所施加阶跃电压的幅值V0与可动板的位移有如下式(6)的关系

(6)

(7)

2.2 考虑阻尼的理论计算

在实际MEMS应用中,当两个平行板做相对运动时,其间的气体受到挤压而表现出一种阻尼效应,这种阻尼称作压膜阻尼。压膜阻尼对MEMS结构的动态特性影响很大,阻尼越大,其系统的品质因子就越小。有时可以主动利用这种关系来调节微机械结构的品质因子以降低阻尼对系统的影响[13]。

本小节主要研究静电微执行器受阻尼影响后的特性,考虑阻尼效应的非线性振动方程为式(8)。

(8)

式中:m为可动板的质量。为了考虑阻尼条件下的Pull-in失稳特性,引入新变量固有频率ω0和阻尼比ζ与阻尼系数μ相关联[1],其中,阻尼比ζ为阻尼系数μ与临界阻尼系数μr之比,式(9)为各变量之间的关系。

(9)

则式(8)可表示为:

(10)

可见,这是一个非线性常微分方程,难以获得精确的解析式。因此,下文中有关考虑阻尼的理论值通过MATLAB,采用龙格-库塔法[8]对式(10)进行微分方程的求解,并与ANSYS仿真值进行对比,从而研究阻尼对于系统的动态特性规律。

3 算例分析

本节主要采用商业FEM软件ANSYS对穿孔板微执行器进行动态仿真,对平行板和带状效率α分别为72.73%、63.64%、54.55%的穿孔板进行仿真,带状效率α=d/(孔间距),定义α为孔-孔边缘间距与孔-孔中心间距之比[14],仿真模型俯视图如图4所示。

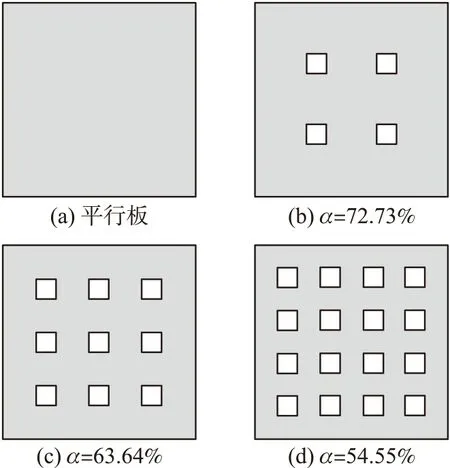
图4 仿真模型俯视图

器件所采用的基本结构参数和其他仿真参数如下:可动板长l为50 μm,宽w为50 μm,厚h为2 μm;孔边长a为5 μm,可动板与固定板的初始间距g0为2 μm;真空中的介电常数ε0为8.854×10-12F/m,空气的相对介电常数εr为1;可动板的杨氏模量E为70 GPa,材料密度ρ为2 700 kg/m3;根据固支梁弹性系数[14]计算公式k=4EWleg(h/Lleg)3,可得等效的弹簧弹性系数k值为35.84 N/m。

ANSYS仿真涉及到静电场与结构场之间的耦合,进行静电结构耦合分析,就得解决静电场与结构场之间参数交换的问题,因此在分析过程中在两个场接触面创建TRANS126单元[15]。TRANS126代表将能量从静电场转换到结构场的转换单元,充分耦合了机电领域。

3.1 压膜阻尼对Pull-in电压影响

图5为不同阻尼比下,在平行板间施加45 V电压的仿真图。从图5可以看出,对于相同规格的微执行器,因为有压膜阻尼的存在,系统的总能量在振荡过程中不断耗散,随着阻尼比的增大,可动板在第一周期内到达的最大位移将减小,动能和势能的最大值也将不断减小,因此临界Pull-in电压值也会因压膜阻尼的存在而产生变化。

图6为对于不同带状效率的可动板,阻尼比对Pull-in电压的影响。

图5 不同阻尼比下,电压45 V时平行板的振荡曲线

图6 阻尼比与Pull-in电压的关系

从图6可以看出,通过龙格-库塔法求解出的Pull-in电压理论值与ANSYS仿真值基本吻合,并且,不管是在哪一种结构中,压膜阻尼效应均会使得其Pull-in电压比忽略阻尼情况时增大;当阻尼比小于0.4时,微执行器所需要的动态 Pull-in 失稳电压会随着阻尼比的增大而增大;当阻尼比大于0.4时,动态Pull-in电压将与其静态 Pull-in 电压值一致。

3.2 压膜阻尼对Pull-in位移影响

对于静电微执行器,Pull-in参数不仅有Pull-in电压,也有Pull-in位移,下面对不同的可动板进行ANSYS仿真,通过MATLAB的拟合功能,对得到的离散点进行拟合,得到不同的阻尼比对Pull-in位移的影响,如图7所示。

从图7可以看出,不管是在哪一种结构中,压膜阻尼效应均会使得其Pull-in位移比忽略阻尼情况时减小;当阻尼比小于0.5时,微执行器的动态Pull-in位移会随着阻尼比的增大而减小。并且当阻尼比大于0.5时,动态Pull-in位移将稳定在其静态Pull-in位移附近。

图7 阻尼比与Pull-in位移的关系

4 结论

本文研究了穿孔板静电微执行器的动态Pull-in现象,通过能量法分析和ANSYS仿真,对忽略和考虑空气压膜阻尼两种情况下的Pull-in参数进行对比,结果表明:压膜阻尼效应会增大动态Pull-in电压,减小动态Pull-in位移。当阻尼比大于0.4,动态Pull-in电压将增大到静态Pull-in电压;当阻尼比大于0.5,动态Pull-in位移将减小至静态Pull-in位移处。