用于压电换能器的频率跟踪驱动电路设计*
段 誉,余厉阳,邹 林
(杭州电子科技大学电子信息学院,杭州 310018)
现有理论认为压电陶瓷工作于其谐振频率时品质因数最高,因此压电换能器大都工作于谐振频率,驱动电路也常常根据换能器的谐振阻抗来设计,为了系统稳定工作而设计的锁频电路也都锁定在谐振频率。但是,这一理论忽略了当不同压电损耗因子耦合时损耗会下降的情况。最近由Shekhani和Uchino根据上述原理完成的实验证明[1-2],压电换能器的最高机械品质频率点出现在谐振频率和反谐振频率之间。由于最佳驱动频率的高机械品质因数,此时的压电换能器获得了更高的效率,并降低了损耗减小了发热。但是即使运行在最佳频率下,换能器的发热情况依旧明显,发热导致的频率偏移在固定频率的驱动方式下会导致工作效率大幅下降,因此本文根据这一现象,设计了一套针对最佳驱动频率运行原理的频率跟踪驱动电路。
在本文中,系统使用朗之万(Langevin)型压电换能器作为载体,验证了假设的可行性。首先,通过恒定振动速度的测量方法测算出最佳驱动频率。通过不同频率下实际输入功率的大小得出谐振与反谐振频率之间的最低功耗频率。再对换能器与驱动电路间做滤波与阻抗匹配处理。最后,提出了一种频率自动跟踪驱动电路,其被设计为能以谐振频率或最佳频率、定频或自动锁相变频方式驱动超声换能器。进行测试试验后,详细的实验结果显示了频率自动跟踪驱动方法的优点。
1 原理依据与实验环境
1.1 最佳驱动频率
压电材料有3个基本的损耗因子:介电损耗,弹性损耗和压电损耗。在损耗的研究中压电损耗通常被理想为零,对它的关注很少。然而根据美国宾夕法尼亚州立大学研究中心早前研究报道可知[3-4],只有压电损耗影响较大才能解释压电换能器在谐振频率和反谐振频率下测得机械品质因数的较大差异。结果表明,压电损耗不仅是不可忽略的,而且较之其他两个因子更大。由Uchino的推导公式[5]计算可得压电换能器的通用损耗因子变化曲线,如图1 所示。计算表明,最高机械品质因数频率出现在谐振与反谐振频率之间。
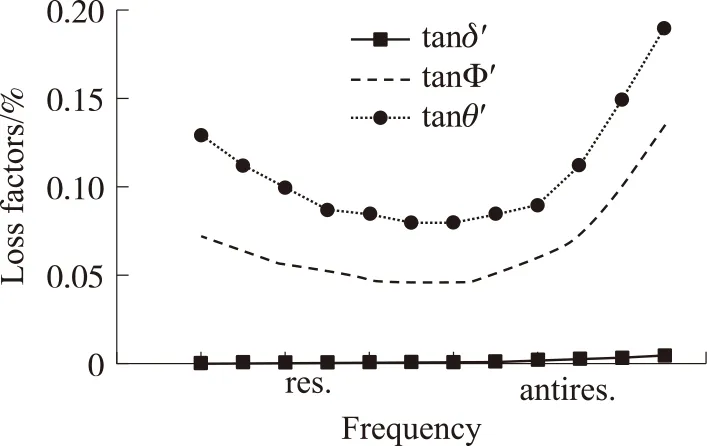
图1 损耗因子趋势图
为了验证最佳驱动频率原理是否正确,实验系统参照文献介绍的高功率压电表征系统(HiPoCS)[6]自行设计了换能器的测试系统,如图2所示。
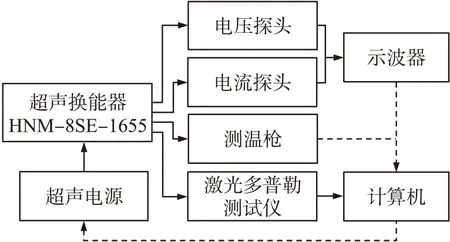
图2 测试系统图
系统检测换能器工作电压电流以得到此时的输出功率,大多数设计测得的都是换能器的视在功率(VI),而考虑到相位差的实际功率(VIcosφ)才为换能器实际储存的能量。

(1)
式中:f为频率,m为质量,v为振动速度,Pd为实际功率。
系统恒定换能器振动速度30 mm/s RMS,从55 kHz频率开始以50 Hz为步进扫频至56 kHz。测试结果表明,最佳驱动频率(fopt)位于谐振频率(fR)和反谐振频率(fA)之间。如图3所示,与谐振频率相比,最佳频率处的机械品质因数接近2倍。

图3 Q值变化曲线
1.2 温升影响
实验中使用的换能器(HNM-8SE-165)由苏州海纳科技有限公司提供,使用阻抗分析仪测试后得到了在室温15 ℃下的阻抗、相位图,如图4所示。

图4 换能器阻抗、相位特性曲线
在使用换能器时,随着工作时长增加,其本身温度会有所上升,原因在于如前文所述压电材料工作时存在的各种损耗。随着换能器温度的升高,其本身的压电参数也会发变化,最直观的反映即换能器本身的谐振频率、反谐振频率同时发生偏移,即换能器温度上升,谐振、反谐振频率下降[7]。如果此时保持换能器的驱动信号频率不变,必然会因为此时换能器新的阻抗值以及变化后的谐振、反谐振频率而产生种种影响,尤其是在谐振频率与反谐振频率附近,换能器本身的电压电流相位差、实际阻抗值变化非常剧烈,如图4所示。经实测,当换能器温度上升至18 ℃,此时谐振频率为(55.2±0.05)kHz,反谐振频率为(55.74±0.05)kHz,等同于驱动频率从谐振点偏移至图4中A点,此时不仅电压电流相位差产生,导致实际输入功率减小,阻抗也增大了近6倍。这些因素的变化都会影响换能器的正常工作,因此驱动电路能否及时作出反应改变频率对于换能器至关重要。
2 频率跟踪系统
频率跟踪系统包括LC滤波、阻抗匹配、采样、相位差检测、驱动电路等部分组成。

图5 频率跟踪系统框示图

图6 驱动电路实物图
2.1 LC滤波
测试表明,采用传统方波驱动换能器,换能器输入电流波形抖动剧烈,如图7类正弦波所示,导致采样后的波形(图7方波)多次过零,无法完成有效的电流相位和有效值采样。究其原因是由于电压从高电平到低电平的切换过程中,电感电容振荡引起。

图8 换能器多谐振频率点图

图7 电流波形(正弦)与采样到有缺陷的电流相位波形
换能器存在多个谐振频率点,如图8阻抗分析测试图所示,对应多个振动模态。如果使用方波驱动换能器,在换能器多点频率工作特点下,信号匹配度差,能量反射严重,极大影响效率。为此,增加了LC滤波电路,滤除了方波中大部分的高次谐波分量。加滤波电路前测试结果如图9所示。加滤波电路后,测试结果如图10所示,电流波形无任何抖动,达到了设计初衷。

图9 滤波前电压(方波)电流(正弦)波形
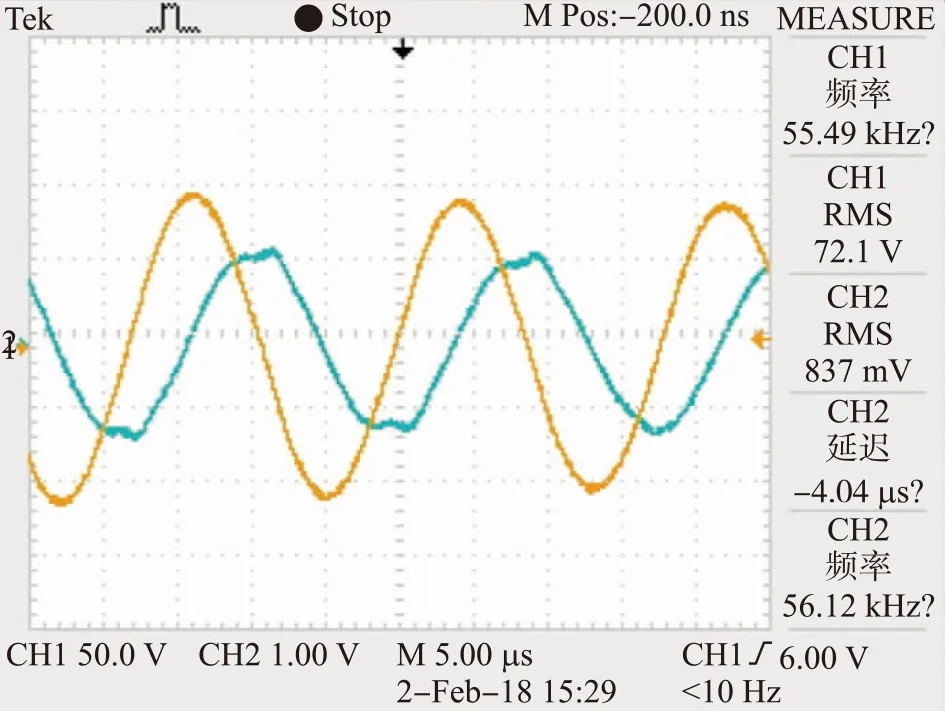
图10 滤波后电压(规整)电流(畸变)波形
2.2 换能器阻抗匹配
换能器等效电路模型参照了改进后的BVD等效模型[8],阻抗分析仪测得换能器电路参数如表1。

表1 换能器电路参数
根据电路理论,换能器的阻抗公式为[9]:
(2)
式中:电阻分量Rz、电抗分量Xz分别为:
(3)
(4)
换能器在串联谐振状态下呈现容性负载,故采用串联电感的方式,如图11(a)。而在换能器最佳驱动频率55.563 kHz下,电压滞后于电流,呈现感性负载,此时应串联电容,如图11(b)。
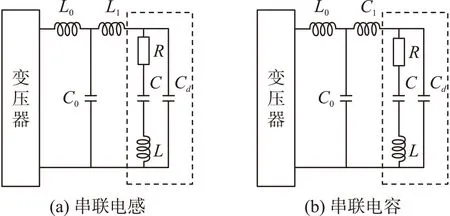
图11 阻抗匹配电路图
当换能器工作于谐振频率,串联电感后换能器的等效总阻抗为:
(5)
当换能器处于串联谐振状态时,加入匹配电感后电路呈现纯阻性,故Xs=0,计算可得L1=1.808 549 635 μH。
当换能器处于最佳工作频率时,换能器阻抗为Zp=90.16 Ω+j763.599 Ω,串联电容计算公式为:
C1=1/[ωp×img(Zp)]
(6)
式中:ωp为最佳频率角频率ωp=2πfp,img(Zp)为最佳频率点阻抗Zp的虚部。计算得C1=23.569 nF。
2.3 数字锁相电路
本系统利用换能器工作于最佳工作状态时,输入电压电流波形相位差固定,并且唯一这一模式,采用锁定电压电流相位差的方式,跟踪最佳工作频率点的漂移,有别于已有的最大电流跟踪、负载跟踪等锁频方式。
系统设计为通过计算电压电流相位差信号脉冲时长得出实际相位差,所以获得换能器相位差是锁相电路的全部目的。如图12,在采样到电压电流信号(非有效值)之后,会先经过由LM339组成的过零比较器,对信号滤波。滤波后的信号交由CD4013检测相位差。通常,相位差检测电路只使用图右侧的两个D触发器(即U1和U2)[10-11],其中一路输出是为相位差脉宽信号,另一路是上一路的反向,但是仅凭这两路信号无法判断电压电流之间的超前或者滞后状态,所以本文对传统的检测电路进行了改进,使设计能够输出超前滞后状态。

图12 相位检测电路图
设计最终输出为一路电压超前信号,另一路电流超前信号,输出信号最终交由FPGA算法计算、处理。
2.4 FPGA算法
因为系统需要支持多线程作业,因此本文设计使用FPGA控制驱动电路,本文的控制算法也基于verilog设计。具体的流程图如图13所示。
与单线程流程图不同,本文同时有两条主要流程:电流检测流程和相位检测流程。相位检测流程用于检测相位差检测电路传输的脉冲以得到电压电流相位差并换算最终得到频率变化量,电流检测流程用于检测采样电路采样得到的电流最大值,用于系统判断。
很明显,结合前文所述,对于最佳驱动频率,仅只依靠相位检测法跟踪频率是很困难的,在最佳频率附近电压电流的相位差变化仅在几度左右,相较之下此时换能器的阻抗值变化更明显,此时检测换能器电流波形最大值更为合适。依靠采样电路与电流检测流程协作,在记录下初次稳定工作时的电流值之后,系统会定时检测电流值的变化,当变化量超过预设的阈值后,系统会通过测得的电流值与此时的电压值换算得到阻抗的大致范围,最后得出是否变化频率以及频率变化量为多少。
与此同时,相位检测流程会保持运行,通过检测电压电流相位差粗调频率使之保持在谐振频率与反谐振频率之间的一个大致的频率区间内,使系统不会因为环境因素骤变导致的换能器频率偏移而跑飞。
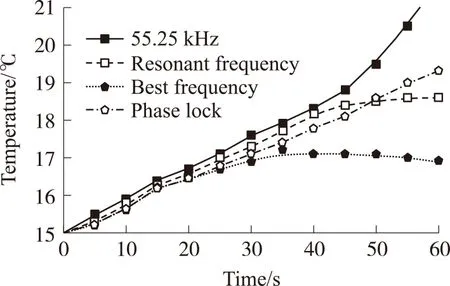
图14 空载结果图
3 实验结果
在完成驱动电路的修改后,我们进行了换能器空载与带载两种实验。
空载试验时以输入功率(500±50)mW为条件,设定了55.25 kHz、谐振频率最佳频率和频率跟踪最佳频率的各自输入电压。实验结果如图14所示。频率55.25 kHz样本由于频偏变为谐振频率,在18.3 ℃后温升曲线骤然变陡。与之相反,因为频偏导致谐振频率偏移,原本的谐振频率样本因为电压电流相位变化以及换能器阻抗值骤然增大,在18.1 ℃后已不能正常工作,温度呈下降趋势。如图2,定频状态下的最佳频率样本附近相位变化相对平缓,但是由于阻抗值大幅增加导致实际输入功率减小,相较于加入频率跟踪的最佳频率样本,定频样本在17 ℃之后就无法保持原有的工作状态了。
在图中我们发现了一个与预计不符的现象,依照空载时有效输入功率都会转化为热能的原理,当换能器初试稳定工作时,各自频率的样本温度应相差不大,但是工作于最佳频率两个样本的工作温度始终比其他两个样本温度要低。考虑到测温枪测试的是换能器压电陶瓷片处温度,温差应主要来自最佳频率较之其他频率更低的压电损耗。如果测量点设定在换能器前后盖板处,温差便没有那么大[12-13]。
而在带载实验中,我们以200 N的压力压在换能器的后盖板上使换能器前端与塑料泡沫紧密接触,在输入同样的功率后,我们使用测温枪测试了换能器同一个部位的温度变化,如图15所示。同样运行在锁频状态下,此时的换能器发热,谐振频率样本远大于最佳频率。

图15 带载结果图
4 小结
本文介绍了一种针对压电换能器最佳驱动频率下的频率跟踪驱动电路,以达到高效率和低发热的目的。通过恒定的振动速度实验,验证了最佳驱动频率理论的可靠性。之后针对最佳驱动频率,对驱动电路进行了改进,并解决了其中发现的一些问题,自行设计了针对这一驱动电路的软件算法,最后在空载与带载两种实验环境下进行测试实验。得到的实验结果表明,本文针对最佳驱动频率设计的驱动电路能够有效解决此时换能器因为频偏而导致其无法正常工作的问题,并且工作在此频率下产生的热量损耗远小于工作在谐振频率下,发热量约降低了一半。由于带载实验下的换能器在不同的负载下电压电流波形会有不同的表现,下一步系统将针对不同的负载对系统算法进行进一步的改进。

