在“操作+探究”中获得数学基本活动经验

丁浩勇

（安徽省无为县刘渡中心学校）

《义务教育数学课程标准（2011年版）》指出，通过义务教育阶段的数学学习，学生能够获得适应社会生活和进一步发展所必需的基础知识、基本技能、基本思想和基本活动经验.基本活动经验是学生经历数学活动之后所留下的直接感受、体验和感悟.它既有学生针对有关数学活动而获得的那些直接经验，又有学生经过不同程度的自我反省而提炼出来的个体知识.在教学中，让学生获得基本活动经验，本质上是让学生获得数学直观（直觉），这是学生获得数学发展的源泉.学生积累数学基本活动经验可以从动手操作的活动经验、思维操作的活动经验和综合探究的活动经验等方面进行.

一、积累动手操作的基本活动经验

所谓动手操作的基本活动经验，就是学生在动手操作实践活动中，通过感官、知觉而获得的直接经验.例如，魔术表演是学生喜闻乐见的娱乐活动之一，如果巧妙地把魔术表演融入到课堂教学中，不但能让学生在轻松的魔术表演活动中快乐地学习，而且能积累动手操作的数学活动经验.

案例1：“整式的加减”的数学活动教学片断.

1.猜数魔术表演

教师呈现月历并随机挑选一个月份，在日期中任意框取一个含有16个数字的4×4的正方形区域，然后在一张空白的纸片上写下一个数字并装入信封，信封交给学生保管起来.让学生选取一名代表，从框取的16个数字中随意挑选一个数，再把这16个数中被挑选的这个数所在的行和列上的其他数都划掉.挑选好第1个数后，再在剩下的数中任意选取第2个数，同时去掉框取的16个数中第2个数所在的行和列上的其他数.以此类推，依次选取4个数.试让学生计算出选取的这4个数的和，再打开信封拿出教师起初所写的数字，发现两个数字完全一致.

2.猜数魔术揭秘

（1）如图1，制作一张正整数表，用一个正方形任意框出16个数.按照魔术表演的方法挑选出4个数，它们分别是3，12，18，23，计算这4个数的和是56.再计算位于这个正方形4个顶点的数字2，5，23，26之和，同样是56.

图1

（2）设框出的4×4的正方形区域的第1列的4个数依次是a，b，c，d，而同行相邻的两个数，后面的数比前面的数大1，因此这16个数分布如图2所示.

图2

根据魔术选数的规则，每一行或每一列上最多只能选一个数，也就是说选出的4个数一定是在不同的行和不同的列上，那么它们的和中一定含有字母a，b，c，d，并且每个字母只出现一次.同样，数字1，2，3也各出现一次，所以无论怎样选数，这4个数的和总是为a+b+c+d+1+2+3=a+b+c+d+6.根据月历的排列规律，又有b+c=a+d，所以a+b+c+d+6=2(a+d)+6.再计算四个顶点数字之和为a+(a+3)+d+(d+3)=2(a+d)+6.这就是说，按照魔术选择规则所选的4个数的和总是等于正方形4个顶点数字之和.

【评析】案例1中，教师打破传统教学观念的束缚，巧妙地让学与玩融为一体，把整式的加、减运算和学生玩猜月历中的数字魔术很好地结合在一起.通过魔术的表演与揭秘过程，积累了学生进行数学活动的基本经验，从而引导学生更加深入地学习整式的相关知识，培养了学生的动手操作能力和创新精神.这样的教学，不但没有浪费学生的时间，反而加深了学生对知识的掌握和运用.

二、积累思维操作的基本活动经验

所谓思维操作的基本活动经验，就是学生在思维操作中开展活动而获得的经验，如归纳的经验、类比的经验、证明的经验.它既可以是直接的经验，又可以是间接的经验.在思维操作中获得的经验更多的是策略性、方法性的经验.例如，整式的加、减运算中去括号法则的探究，教师是让学生通过计算与观察、猜想与验证的思维操作活动得出结论的.

案例2：“整式的加减”之探究去括号法则教学片断.

探究1：括号前面是“+”.

（1）计算.

①5+(3-1)=5+___= ____；

5+3-1= ____- ___= ___.

观察一下，5+(3-1)与5+3-1相等吗？

②5+(3+1)=5+___= ____；

5+3+1=___+ ___= ____.

观察一下，5+(3+1)与5+3+1相等吗？

（2）猜想：a+(b+c)和a+b+c的大小关系怎样？

（3）验证.

①实际问题验证：丁丁去超市，买水果用去了a元钱，买钢笔用去了b元钱，买圆规用去了c元钱，丁丁在超市一共花费了______.

这个问题还可以这样来解决，丁丁买水果花费了____，买文具（钢笔和圆规）花费了______，丁丁在超市一共花费了______.

这样我们就得到等式______= _____.

②乘法分配律验证：类比数的运算，有a+

（4）结论：如果括号外的因数是正数，去括号后原括号内各项的符号与原来的符号______.

探究2：括号前面是“-”.

（1）计算.

①5-(3-1)=5-____= ____；

5-3+1=___+ ___= ____.

观察一下，5-(3-1)与5-3+1相等吗？

②5-(3+1)=5-___= ____；

5-3-1=____- ____= ____.

观察一下，5-(3+1)与5-3-1相等吗？

（2）猜想：a-(b+c)和a-b-c的大小关系怎样？

（3）验证.

①实际问题验证：丁丁带了a元钱去超市，买文具用去了b元钱，这时剩下的钱数为______，接着又买水果用去了c元钱，丁丁最终剩下的钱数为______.

这个问题还可以这样来解决，丁丁在超市买文具和水果一共花费了______，丁丁最终剩下的钱数为_____.

这样我们就得到等式______= _____.

②乘法分配律验证：类比数的运算，有a-

（4）结论：如果括号外的因数是负数，去括号后原括号内各项的符号与原来的符号________.

【评析】根据认知心理学，学生的知识形成过程是外来信息与学生原有知识和思维结构相互作用的过程.学生的数学能力是通过活动作为中介形成的，在活动中思考，在活动中创新，在活动中得到发展.本案例中，教师分两步（括号前面是“+”和括号前面是“-”）让学生探究去括号法则，每一步又是通过学生先计算具体数字的带括号与不带括号的相关算式题，计算出结果后再进行比较，观察它们的值是不是相等，由此猜想得出用字母表示数的一般情况的结论.然后再通过学生熟悉的实际问题和学生已有的知识（乘法分配律）加以验证，学生通过这一系列的思维操作活动，最终得出去括号法则.这样的教学，不仅有利于积累学生思维操作的基本活动经验，而且有利于培养学生解决问题的能力和探索精神.

三、积累综合探究的基本活动经验

所谓综合探究的基本活动经验，就是学生立足于已有的问题，围绕问题的解决而开展的活动，这里的活动既有外显行为的操作活动，又有思维层面的操作活动.同时，这种探究的直接价值取向是问题解决，而不仅仅为了获取直接感受、体验和经验.

案例3：“锐角三角函数”的数学活动教学片断.

1.拼图魔术表演

教师展示如图3所示的一个由4块积木拼成的直角三角形，然后把这4块积木打乱，再从口袋中掏出一小块正方形积木，用这5块积木重新拼成一个如图4所示的与原直角三角形“全等”的新直角三角形.观察图3和图4，这两个直角三角形的两条直角边分别相等，都是5和13.明明增加了一块积木，按理说，图4的面积要比图3的面积大1，怎么会前后两个三角形的面积仍然不变呢？

图3

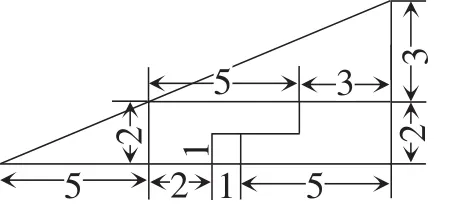
图4

2.拼图魔术揭秘

（1）动手操作，发现问题.

学生在纸板上先画一个边长为13 cm的正方形，用剪刀按图5的尺寸把它裁剪成4部分，然后再把这4部分按图6的样式重新拼接，分别计算这两个图形的面积.

图5

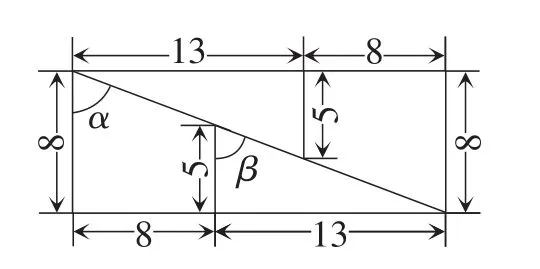
图6

正方形的面积是13×13=169 cm2，矩形面积是21×8=168 cm2.相同的4块拼成的不同图形后，面积一个是169 cm2，一个是168 cm2，怎么又少了1 cm2呢？

（2）理论验证，解决问题.

分别计算图6中的∠α和∠β的正切值，看一看这两个角是否相等？

所以tanα≠tanβ.所以∠α≠∠β.

这就是说在拼接矩形的过程中其对角线附近发生了微小的重叠，这微小的重叠，人的眼睛是很难发现的，正是这微小重叠导致了前后两个图形面积的变化.

【评析】苏霍姆林斯基说过，在每一个孩子的心灵深处，都有一种根深蒂固的需要，那就是希望自己是一个发现者、研究者、探索者.课堂上，教师应该成为学生探索路上的导航员.案例3通过增加一块积木后重新拼图却能拼出与原来“一模一样”的图形，立刻就触动了学生强烈的好奇心，这时教师趁机投影展示问题，让学生动手画图剪纸，亲自拼图验证，最终通过计算三角函数值来探究拼图的奥秘，这样使学生真正成为发现知识、获取知识、创造知识的主人.本次活动中，既有外显行为的画图剪纸的动手操作活动，又有思维层面的应用三角函数知识进行运算的操作活动，这样的教学可以很好地积累学生综合探究的数学活动经验.

总之，真正让学生动起来是落实“积累数学活动经验”课程的核心要素，实践与自主是“积累数学活动经验”课程的精髓.我们在课堂教学中一定要努力为学生提供具有现实性、丰富性和挑战性的数学活动，来拓宽学生的视野并提升学生的数学思维，以达到积累基本活动经验的目的，真正实现由“双基”到“四基”的转变.