纵向耦合驱动式有轨电车μ综合导向控制

杨 哲， 陆正刚， 李道军， 黄 琦

(同济大学 铁道与城市轨道交通研究院， 上海 201804)

有轨电车作为现代城市轨道交通的重要组成部分，其通常会采用独立旋转车轮以方便车轴下凹，使车内空间可以做成100%低地板形式.由于独立旋转车轮同轴两侧车轮可以独立转动，所以当左右两侧车轮存在轮径差时其纵向蠕滑力不足以产生使车轮恢复对中和导向的摇头力矩，因此低地板有轨电车直线运行时在轨道横向激励作用下容易造成车轮轮缘和钢轨的接触；车辆曲线通过时由于缺乏自导向能力，独立旋转车轮的轮缘和钢轨会持续贴靠[1-2]，增加车辆运行阻力和轮轨磨耗，从而增加车辆运营和维护成本.采用横向耦合或者纵向耦合形式的转向架可以一定程度上提高低地板有轨电车的导向能力.其中纵向耦合转向架同侧前后两车轮用同一电机驱动，以保证其转速一致(也可用电器耦合的方式实现).由于纵向耦合转向架直线对中和曲线导向能力不如采用传统轮对的转向架[3]，而有轨电车运行线路曲线多且半径较小，所以采用纵向耦合转向架的有轨电车运营时磨耗严重.

随着机电一体化技术的发展，主动控制在轨道车辆上得到了越来越广泛的运用，其中欧洲的主动倾摆式列车便是典型案例.由于主动导向控制能有效减小轮轨磨损和能量消耗[4]，因此国内外学者针对轨道车辆主动导向控制开展了广泛的研究，但考虑轮对纵向耦合的研究未见报道.Wickens[5]采用比例(P)控制，实现了采用 “独立旋转轮对副”轨道车辆的小曲线通过主动控制.但是P控制不能消除稳态误差，且响应迟缓，不适用于高频轨道激励工况.德国宇航局在下一代列车项目[6]采用比例-微分(PD)控制算法控制独立旋转车轮左右两侧电机转矩实现主动导向控制.任利惠等[7-8]采用比例-积分(PI)控制，以车轮速差和曲线半径等因素为反馈量实现独立旋转轮对车辆的主动控制.Gretzschel[9]、孙效杰等[10]采用比例-积分-微分(PID)控制算法，通过测量车轮横移量和摇头角实现了独立旋转车轮轨道车辆的牵引和导向集成控制.Mei等[11]采用模态控制算法通过控制安装在车轴与构架间的作动器来实现独立旋转车轮的主动导向控制.经典的PD、PI或者PID控制算法，并不能实现控制最优；而模态控制虽然能一定程度上实现最优控制，但由于其基于线性模型设计，而轨道车辆是强非线性系统，所以并不能反映系统的真实情况.

本文采用鲁棒μ综合方法对纵向耦合驱动有轨电车进行主动导向控制，考虑了轮对系统外部激扰不确定性、轮轨系统接触的非线性引起的参数变化和反馈信号的测量噪声，对纵向耦合驱动有轨电车的主动导向技术的实际应用有一定的意义.

1 车辆结构及控制器设计原则

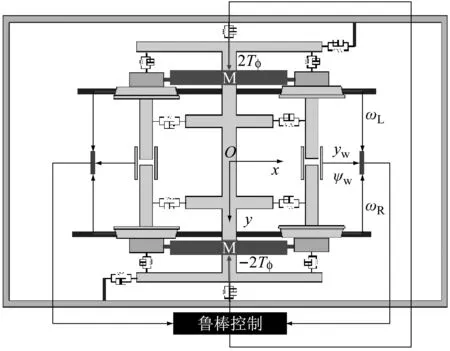
文中研究的有轨电车结构如图1所示，车辆动力学参数见表1，其中转向架同侧前后两车轮由同一电机驱动，形成纵向耦合转向架.对多自由度的整车系统，建立整个系统的状态空间并采用鲁棒μ综合法求解几乎是不可行的，因为鲁棒μ综合法对多自由系统收敛困难，且对系统状态空间要求严格，因此文献[12-13]只对单构架车辆模型进行了控制器设计.由于轮对通过一系悬挂与构架联接、通过轮轨接触与轨道联接，因此如果把一系悬挂和轮轨接触力的合力看作轮对系统的外部输入力，则轮对系统就可以从车辆模型中独立出来.轮对系统上的外部力可表示为控制系统的不确定输入，这样即充分考虑了转向架和车体以及轮轨力对单轮对模型的影响；又避免了采用整车系统的状态方程，使鲁棒控制在复杂的整车模型中得以应用.

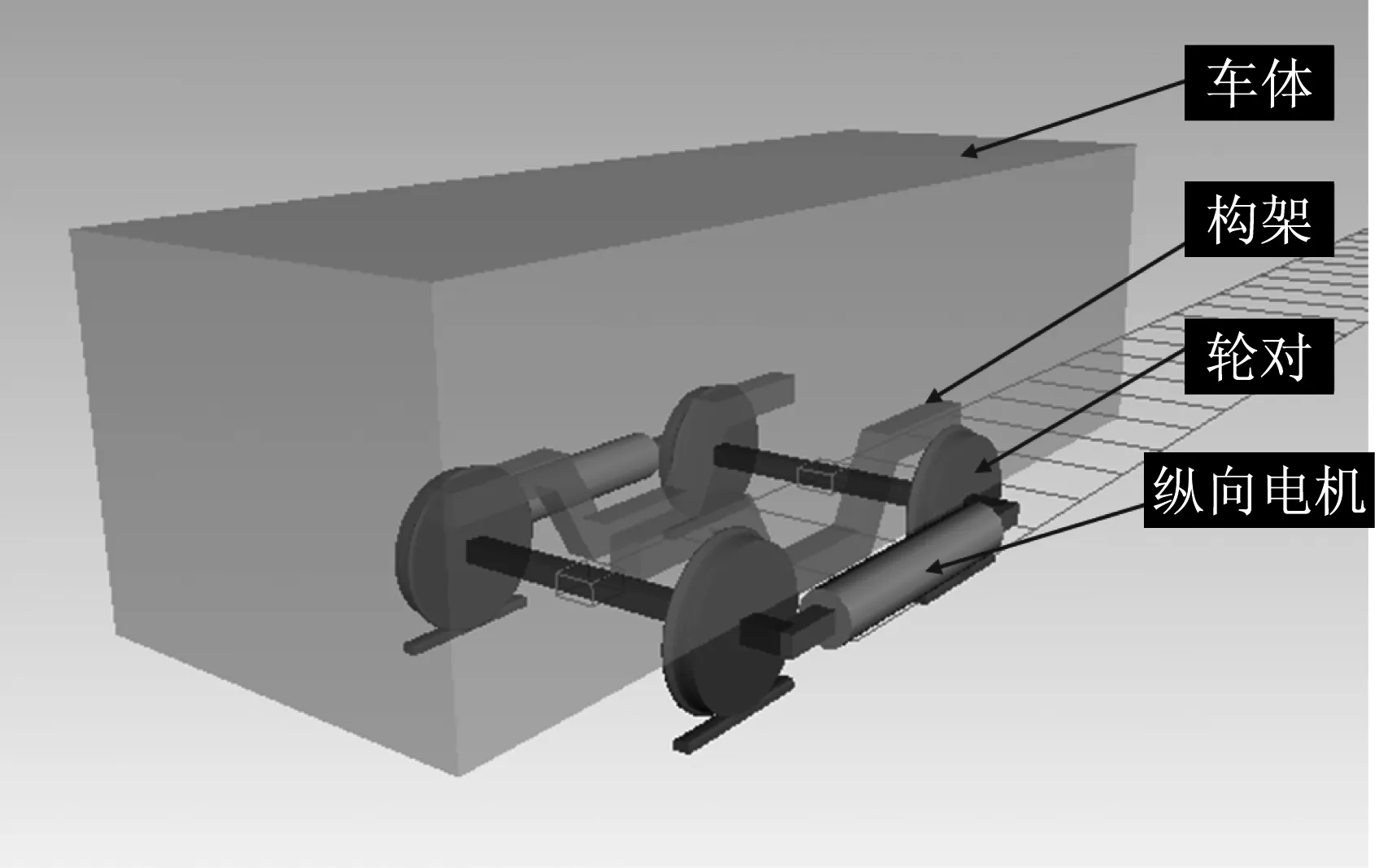
图1 纵向耦合有轨电车结构

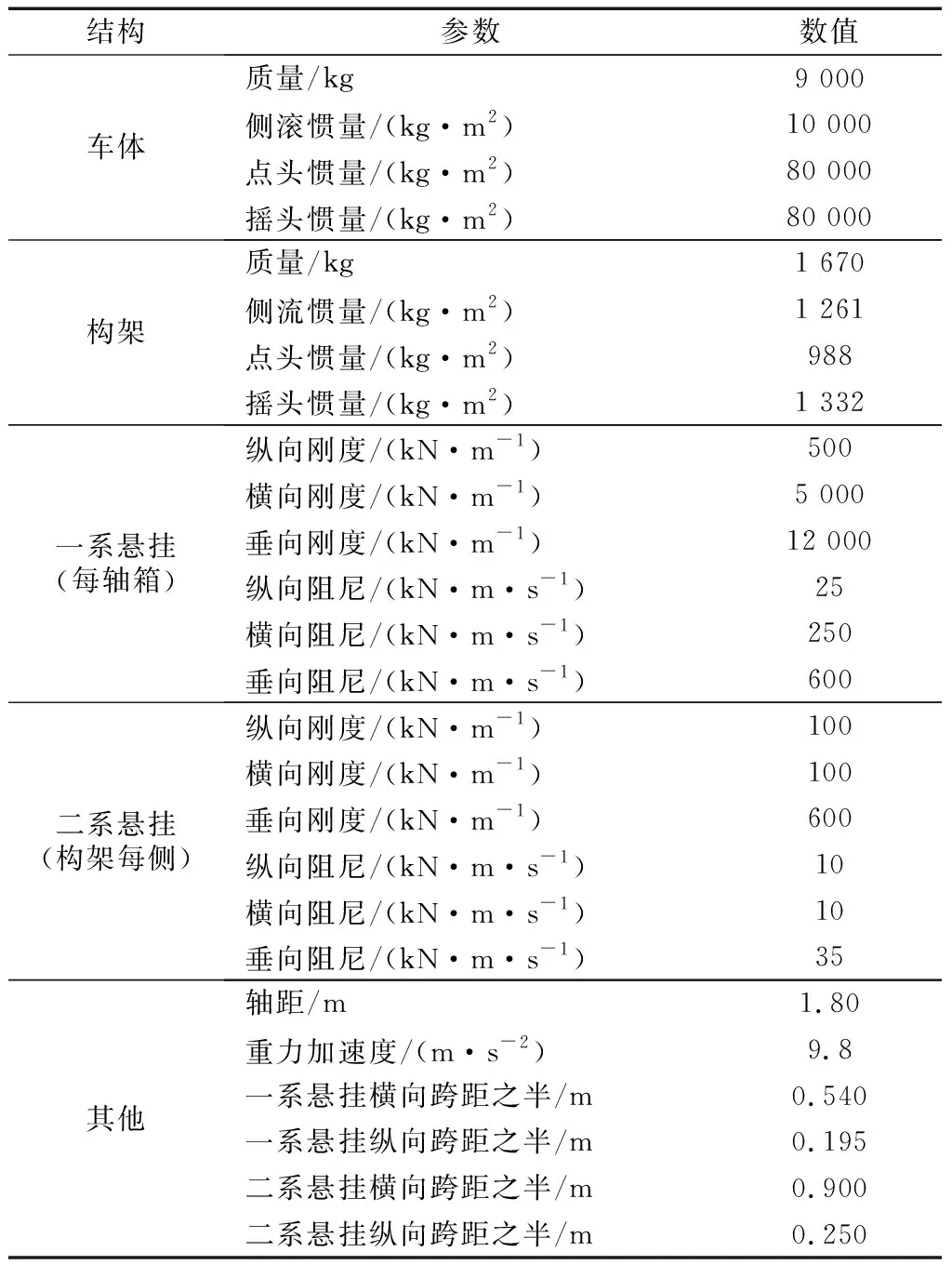
结构参数数值车体质量/kg9 000侧滚惯量/(kg·m2)10 000点头惯量/(kg·m2)80 000摇头惯量/(kg·m2)80 000构架质量/kg1 670侧流惯量/(kg·m2)1 261点头惯量/(kg·m2)988摇头惯量/(kg·m2)1 332一系悬挂(每轴箱)纵向刚度/(kN·m-1)500横向刚度/(kN·m-1)5 000垂向刚度/(kN·m-1)12 000纵向阻尼/(kN·m·s-1)25横向阻尼/(kN·m·s-1)250垂向阻尼/(kN·m·s-1)600二系悬挂(构架每侧)纵向刚度/(kN·m-1)100横向刚度/(kN·m-1)100垂向刚度/(kN·m-1)600纵向阻尼/(kN·m·s-1)10横向阻尼/(kN·m·s-1)10垂向阻尼/(kN·m·s-1)35其他轴距/m1.80重力加速度/(m·s-2)9.8一系悬挂横向跨距之半/m0.540一系悬挂纵向跨距之半/m0.195二系悬挂横向跨距之半/m0.900二系悬挂纵向跨距之半/m0.250

纵向耦合转向架前后轮对除同侧前后车轮转速一致外,其他自由度相互独立[3].因此本文首先以单个轮对为研究对象进行控制器设计，使其获得相对最优的控制策略，然后通过对单个轮对控制器进行不同的组合设计出适合纵向耦合转向架的控制方法.

2 基于单轮对的鲁棒控制器设计

考虑轮对的横移、摇头以及车轮的转动自由度，则独立车轮轮对的动力学方程可以表示为

ψ=Fy

(1)

(2)

(3)

式中：mw=1 250 kg,为轮对质量；IωΨ=700 kg·m2,为轮对摇头转动惯量；Iwφ=27 kg·m2,为车轮的旋转转动惯量；l=0.75 m为轮对横向跨距之半；r0=0.35 m为车轮名义滚动圆半径；y为轮对横移量，m；ψ为轮对摇头角，rad；φ为车轮旋转角度，rad；v为车辆运行速度，m·s-1；f11、f22分别为纵横向蠕滑系数；λ为车轮踏面斜度；Fy和Tψ分别表示由一系悬挂和轮轨力的非线性部分作用在轮对上的合力和合力矩；Tφ是作用在左右轮上控制转矩差之半.

Tφ=TφL，Tφ=-TφR

(4)

式中：TφL,TφR分别是作用在左右车轮上的控制转矩.dφ/dt为左右轮转速差之半，即

ωL=v/r0+dφ/dt,ωR=v/r0-dφ/dt

(5)

式中:ωL,ωR分别为左右轮转动角速度.轮对的动力学方程可写成状态空间形式为

(6)

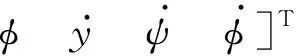
车轮的横移量和摇头角是评价车辆直线对中和曲线通过性能的两个重要指标：轮对相对钢轨的横移量反映出是否发生轮缘与钢轨接触及车辆运动的稳定性，而车轮冲角影响横向蠕滑力的大小.由于同一轮对左右车轮之间有轴桥连接，因此轮对横移量和摇头角是相互关联的，所以导向控制时只需控制轮对横移量的大小即可[10].选取轮对的横移量作为系统输出，并选取轮对相对轨道的横移量、摇头角以及左右轮旋转角度差作为控制系统的测量变量，则控制系统的状态空间可写为

(7)

式中：C1、C2是输出矩阵；D11、D12、D21、D22是前馈矩阵；Ss是系统的状态空间矩阵；Z=y是系统输出；Y=[yψφ]T是测量变量.

2.1 系统参数不确定性及其分离

轮轨接触具有强烈的非线性特性，所以独立旋转车轮的动力学方程并非线性方程.其非线性特性主要是由轨道和车轮踏面的几何非线性和轮轨接触力的非线性产生，即动力学方程中的踏面锥度λ和横、纵向蠕滑系数f11与f22并不是一个固定值，而是在一定范围内变化，因此文中用参数不确定性表示轮轨接触的非线性特性.不确定性变量f11、f22和λ可表示为

δ1)

(8)

(9)

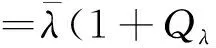
(10)

(11)

由式(11)可知状态空间可表示为名义状态空间与不确定性状态空间之和.利用线性分式变换(LFT)把状态空间中不确定参数表示为系统的外部摄动.首先对不确定状态空间进行奇异值分解(SVD),即

(12)

式中:Li、Hi、Ri是状态空间正交输入基向量，与LFT变换时系统状态和不确定矩阵的输出相关；Si、Ti、Ji是状态空间正交输出基向量，与LFT变换时不确定矩阵的输入相关.结合公式(11)和(12)，可知以下扩展矩阵成立:

(13)

式中：qi和pi分别表示对应不确定性δi的输入和输出,qi=δipi(i=1,2,3)；Gext是扩展状态空间矩阵，包含了由奇异值分解得到矩阵.对扩展状态空间Gext进行两次上线性分式变换可得

(14)

式中：Gnom(s)是扩展状态空间的标称矩阵；

Δ=diagδ1,δ2,δ3

(15)

是系统外部摄动;G(s)是包含参数不确定的状态空间矩阵.此时系统的参数不确定已从原系统中抽离,公式(14)所示的系统可用图2表示.

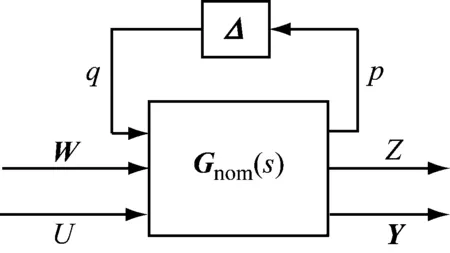
图2 含参数不确定的标准H∞控制

2.2 扩展模型和权重函数

控制器设计时除了使车轮横移满足设计要求外，电机的控制输出转矩也要满足电机的许用输出值，否则控制系统可能无法实现.考虑到对轮对状态进行实际测量时存在测量噪声，对整个控制系统的输入、输出进行归一化处理，可得到符合实际控制系统设计目标的扩展控制系统框图，如图3所示.图中ew、ez、eu和η满足无穷范数小于1，分别是归一化后的外部激扰输入、系统输出、控制器输出和测量噪声输出；Ww、Wz、Wu和Wη是与之对应的权重函数.

图3 扩展导向控制系统框图

其中：

(16)

用来表示作用在轮对上的外部横向力和摇头力矩的变化范围，其由轮轨力与一系悬挂力的合力产生.Ww表示轮对外部横向力在2 500 N以内，摇头转矩在1 400 N·m内.Wz和Wu分别用来约束系统输出和控制器输出，确保车辆在获得导向性能的同时，电机的控制转矩符合许用值.

(17)

是车辆横移输出权重函数，用来约束轮对的横移量在低频时小于4 mm，在高频时不超过6 mm.Wu是电机输出权重函数

(18)

目的是使电机在低频时的输出转矩不超过1 000 N·m，并抑制电机的高频时的输出.Wz与Wu倒数的幅频响应如图4和图5所示.

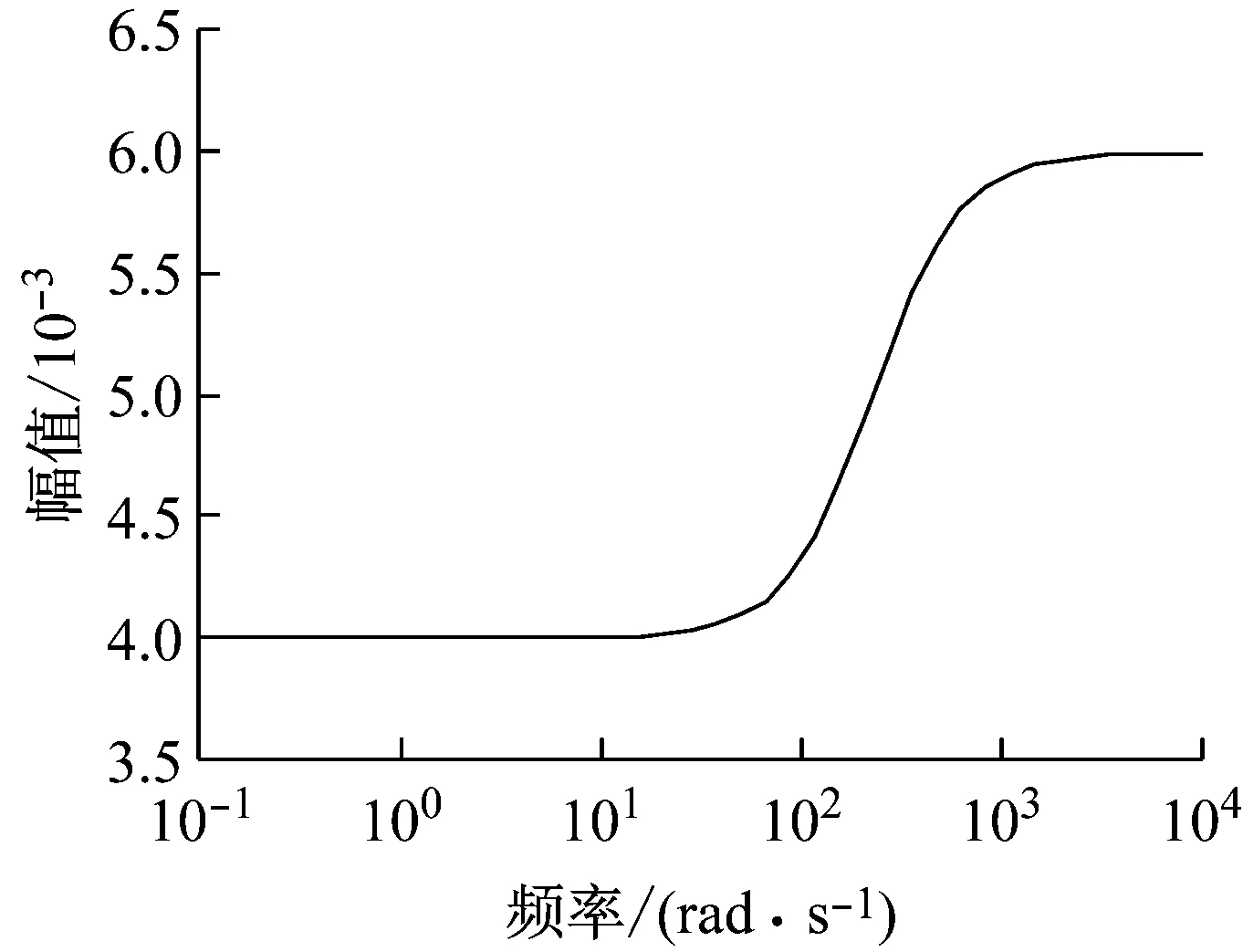
图4 1/Wz的幅频特性

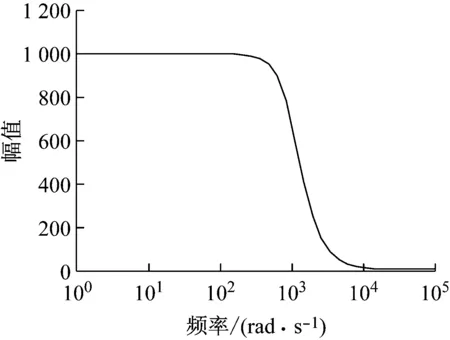
图5 1/Wu的幅频特性

Wη=diag{wη,wη,wη}，其中wη=10-4，以限制测量噪声误差在所有频段均为10-4.

由图3可知,由ew、eη到ez和eu的传递函数为

(19)

式中：So是输出灵敏度函数;Gw与Gu分别是开环系统下外部激扰W和控制输出U到系统输出Z的传递函数;SoGw和SoGu分别是W和U到Z的传递函数;K是待求控制器.则在同时存在参数不确定性、测量噪声、外部不确定激扰的情况下，满足控制器设计目标的充分条件为：求一个真实有理的控制器K，使从由ew、eη到ez和eu的传递函数矩阵的H∞范数满足

(20)

2.3 控制器求解

把图3中虚线框中的部分定义为Gsys(s)，则系统可表示为带有参数不确定的标准H∞控制形式,如图6所示.图6中：Δsys=Δ,ewη=[eweη]T,ezu=[ezeu]T.

图6 扩展控制系统的标准H∞控制形式

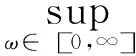
μΔPFl(Gsys,K)(jω)<1

(21)

其中：

公式(21)可转化为关于求控制器K的优化问题.

图7 扩展控制系统的鲁棒性能分析模型

定义常数对角矩阵为

D=diag[D1,D2,D3,I1]

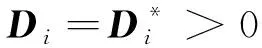
(22)

则公式(21)等价于求解

(23)

利用D-K迭代法，交替优化式(23)中的D和K，最终得到满足系统鲁棒性能的控制矩阵，使系统的结构奇异值小于1，此时闭合系统的结构奇异值μ随频率的变化如图8所示.

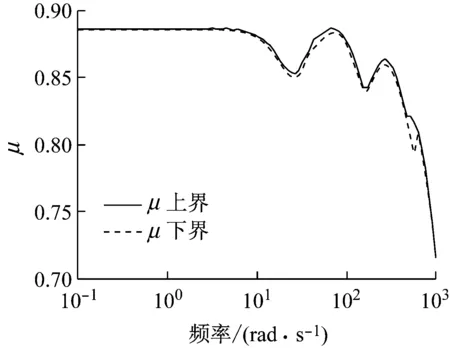
图8 系统的结构奇异值随频率的变化

Fig.8Singularvalues-frequencyresponseoftheclosed-loopcontrolsystem

3 控制效果仿真分析与对比

纵向耦合转向架同侧前后两车轮转速和控制输入相同，而前后车轮对主动控制转矩需求不同，所以纵向耦合转向架无法同时使前后车轮获得最优的导向状态.因此，基于单轮对鲁棒控制器提出3种适用于纵向耦合转向架的控制方案，如图9所示.图9a中采用前轮状态信号作为控制器输入，控制器输出的2倍作为纵向电机的控制信号.因为车辆通过曲线时前轮的磨耗更为严重，所以优先对前轮进行控制；图9b取前后轮对两控制器输出之和作为电机的控制输入；图9c则是以前后轮状态信号的平均值作为控制器输入信号，取控制器输出的2倍作为电机的控制输入.

文中选用两种典型工况对控制效果进行验证，分别是车辆以20 m·s-1的速度直线运行和以8.3 m·s-1的速度通过半径为70 m的曲线，横向激励采用美国5级轨道谱.为充分验证文中提出的μ控制算法的有效性，文中分别将其与施加鲁棒H∞控制与无控制时的效果进行了对比.不同算法的控制效果通过MATLAB和SIMPACK的联合仿真得到.

主动导向控制的根本目的是降低轮轨磨耗，而下文中的仿真结果表明,相较于H∞控制，μ控制可以使车辆获得更小的磨耗数(尤其是在曲线工况上)，使车辆获得更好的导向效果.因此为突出研究重点，下文中只对施加μ控制与无控制时的仿真结果进行对比.

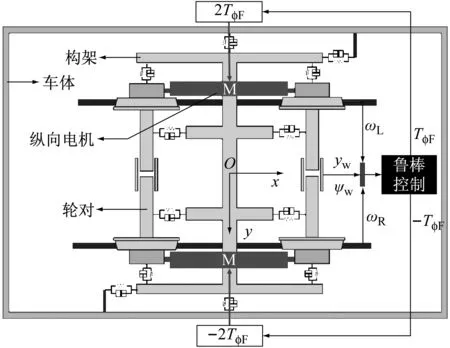
a 控制方案1

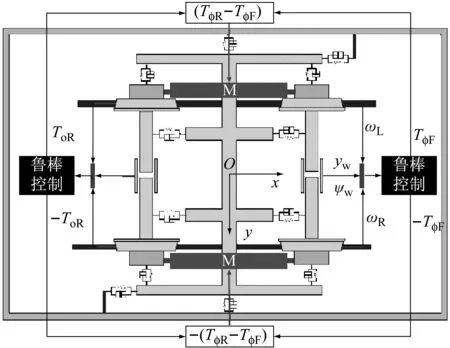
b 控制方案2

c 控制方案3

Fig.9Activeguidancecontrolschemeforlongitudinalcoupledtramcar

3.1 直线工况

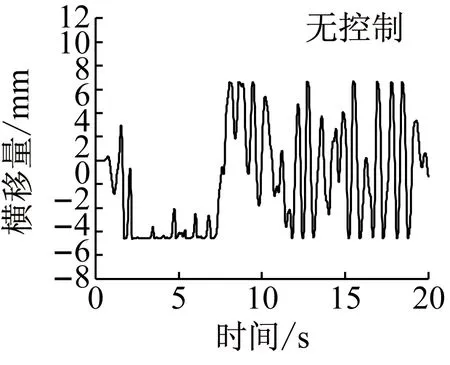
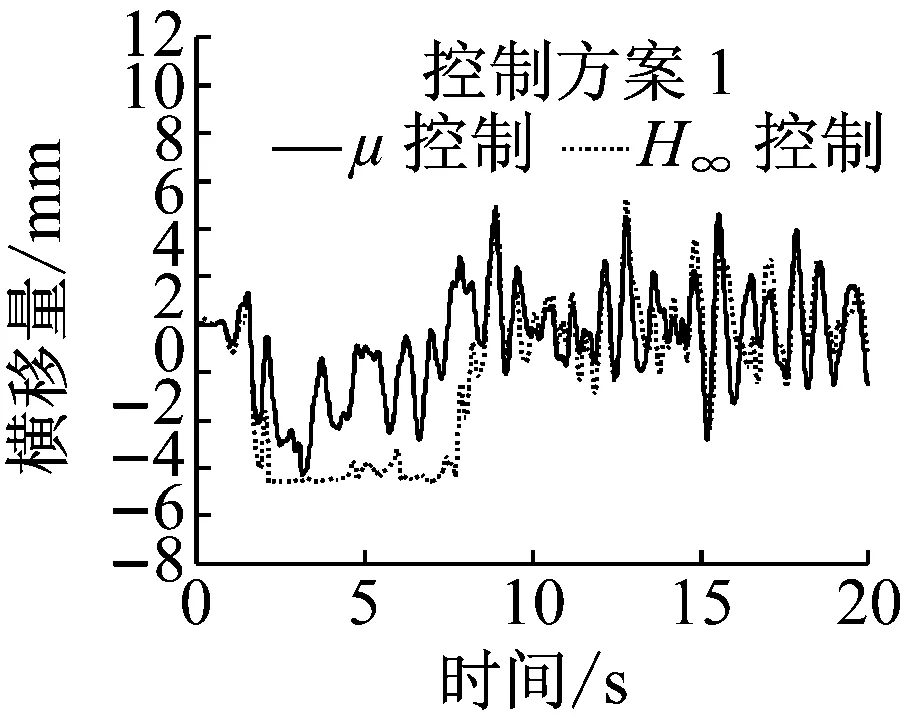
车辆以20 m·s-1的速度在直线运行时，施加控制前后车辆前导向轮对的运行状态如图10所示.无控制时导向轮的横移量最大为7.5 mm，发生轮缘贴靠；摇头角最大为12.6 mrad.此时前轮对的磨耗数最大值为968 N，平均值为16.9 N.当采用控制方案1(仅采用前轮状态进行控制)时，导向轮对的横移量和摇头角的最大值分别是3.8 mm和4.9 mrad，导向轮对获得了很好的直线对中能力.随着车轮横移和摇头的减小，轮对磨耗数的最大值和平均值分别降为296 N和7.4 N.相较于无控制工况，采用控制方案1时导向轮对的平均磨耗数降低了56%.由图10知，此时导向轮对横移量输出符合权重函数Wz的约束值，且控制转矩Tφ在1 000 N·m内，符合控制器鲁棒性能的设计目标.

由于控制方案1只采用了导向轮状态，而纵向耦合转向架同侧前后车轮转速一致，因此控制方案1无法保证后侧轮对的状态最优.施加控制方案1时后侧车轮的状态见表2，可知此时的后侧车轮的平均磨耗数由无控制时的13.2 N增加至23.9 N，后轮的磨耗数增加了81%，因此只采用一个轮对的状态进行控制是不可取的.

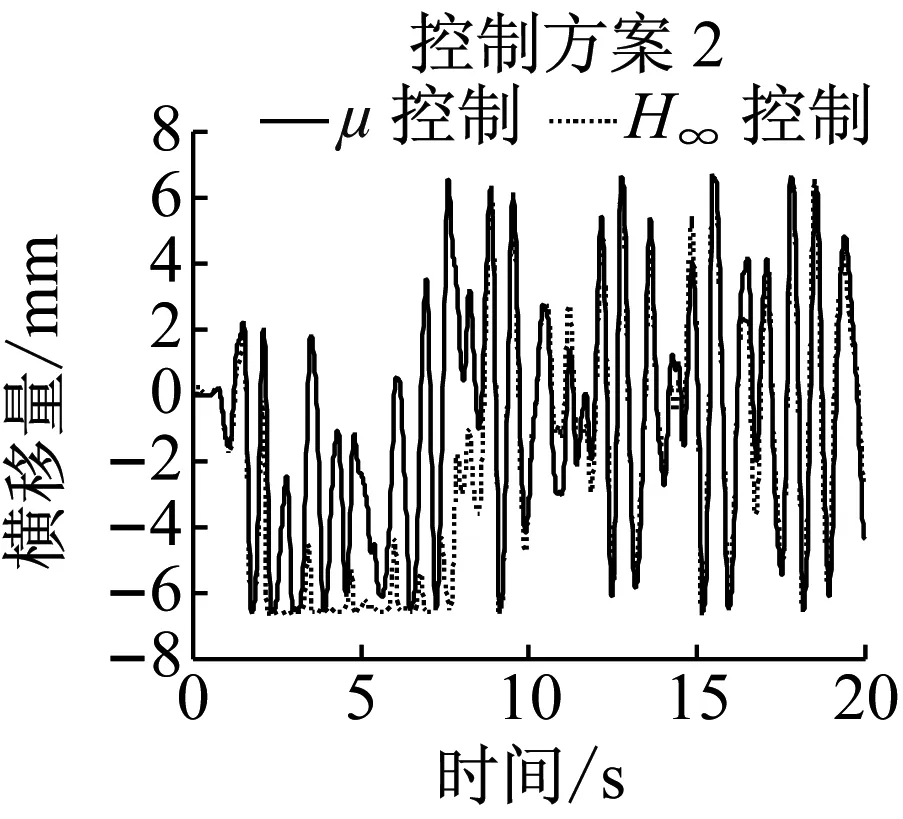
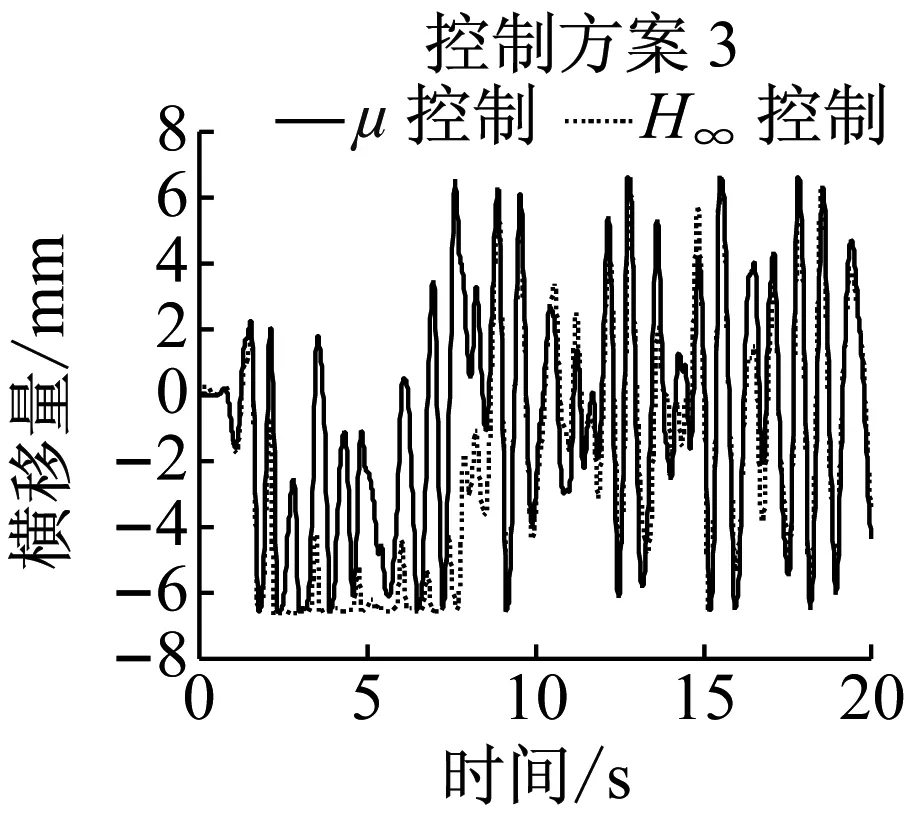
控制方案2和3都综合采用了前后轮的状态，因此对于单个车轮的控制效果不是最优.由图10知，两种控制方案并没有明显地降低轮对横移和摇头的最大值，但轮对横移和摇头绝对值的平均值均明显下降，具体数据如表2所示.导向控制的根本目的是降低车轮的磨耗，因此重点对磨耗数进行对比.由表2可知，控制方案2仅能降低后侧车轮的磨耗数，而导向轮对的平均磨耗数反而增加.而采用控制方案3时，前后轮对平均磨耗数由16.9 N减小为13.2 N，而后侧轮对的磨耗数由13.2 N降低为5.3 N，即控制方案3能同时减低前后轮对的磨耗，综合降幅为38%.因此直线工况下，控制方案3是最优导向控制方案.

3.2 曲线工况

车辆以8.3 m·s-1的速度通过半径为70 m的曲线时，施加控制前后车辆前导向轮对的运行状态如图11所示.由图11a可知，当车辆被动通过曲线时车轮横移量在曲线部分几乎一直保持在6.7 mm左右，说明此时车辆靠轮缘力实现导向.此时导向轮对在曲线期间磨耗数均值为85 N.采用控制方案1时，导向轮对最大横移为6.3 mm，避免了轮轨贴靠.曲线通过时导向轮的平均磨耗数为39 N，与被动导向相比降低了54%.导向轮单侧控制转矩最大值为877 N·m，小于最大允许值1 000 N·m，满足控制器设计目标.此时侧车轮的状态见表3，可知此时的后侧车轮的平均磨耗数同样得到了减少，由无控制时的27.1 N降至21.6 N. 可见曲线通过时，只采用前轮状态进行控制器设计仍能同时降低前后轮对的磨耗.

表2 直线工况控制前后轮对状态

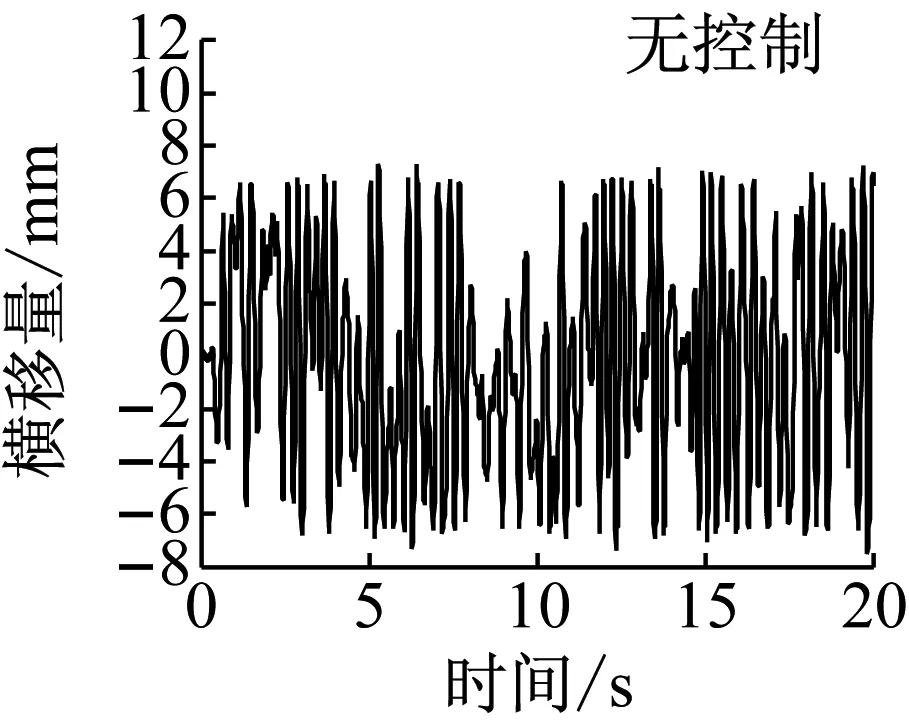
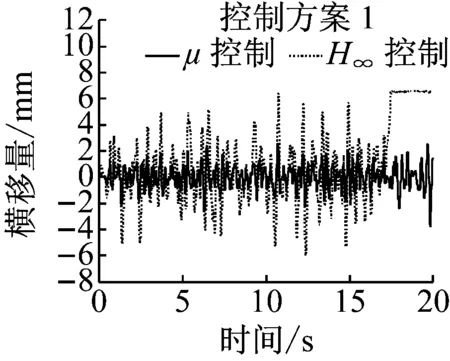
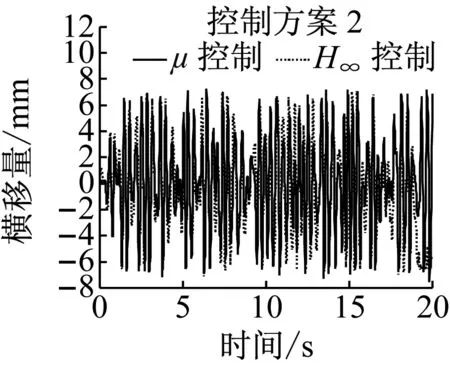
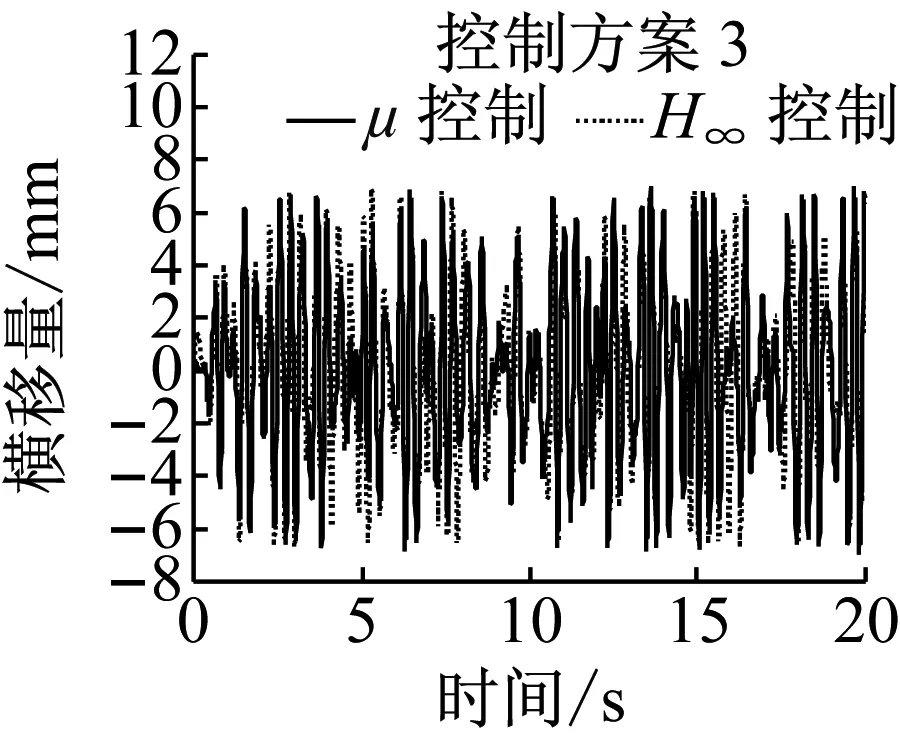
a 横移量

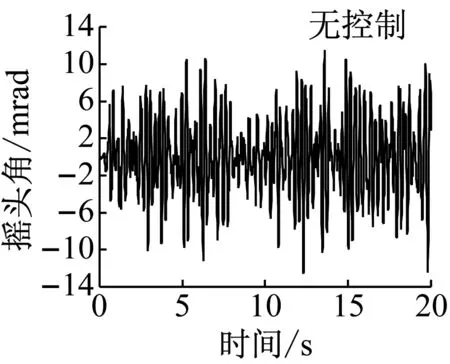
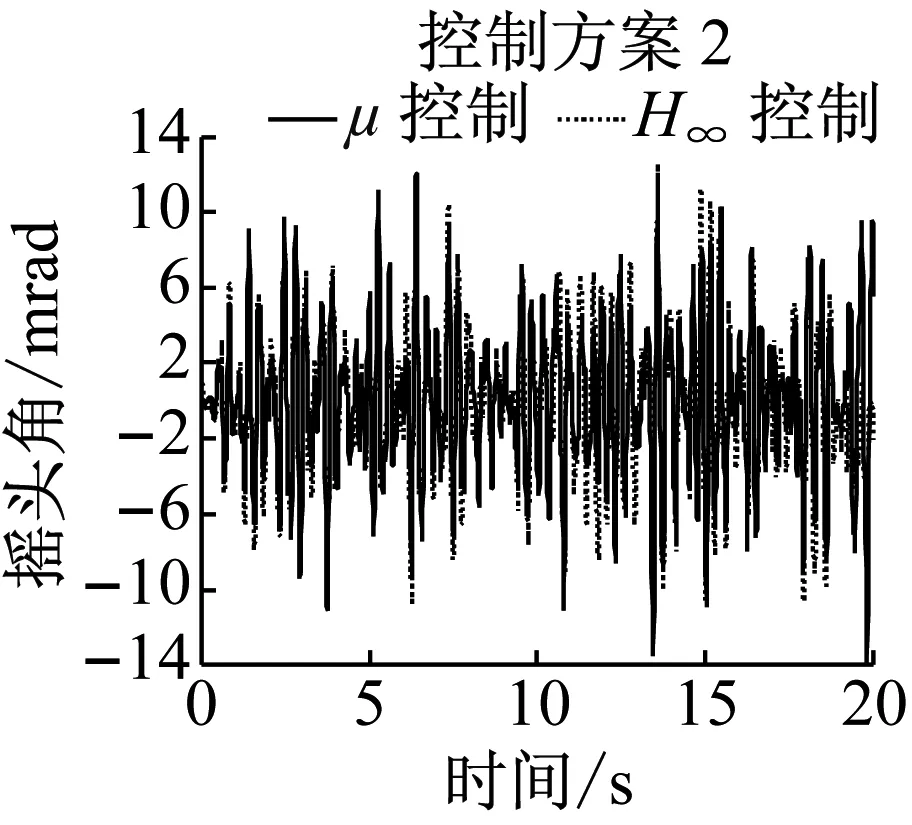
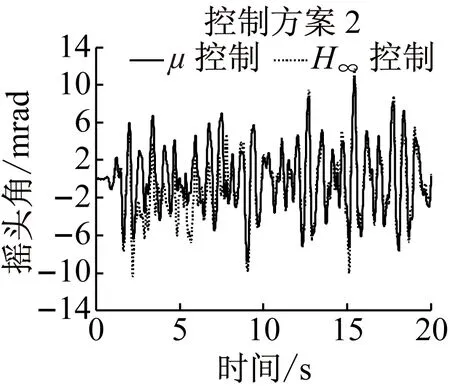
b 摇头角

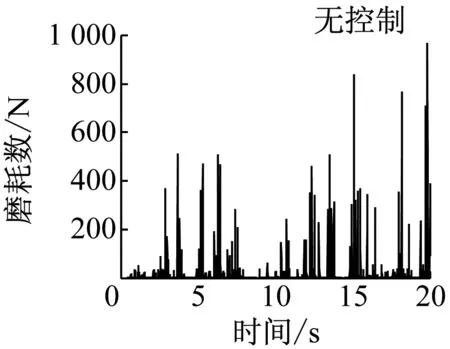
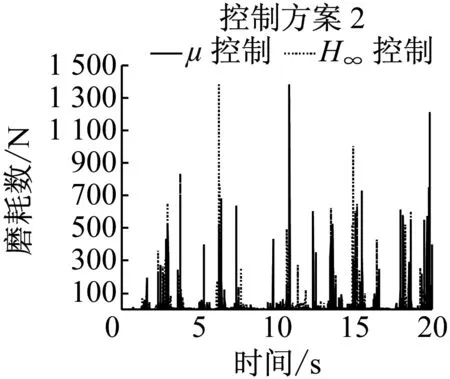
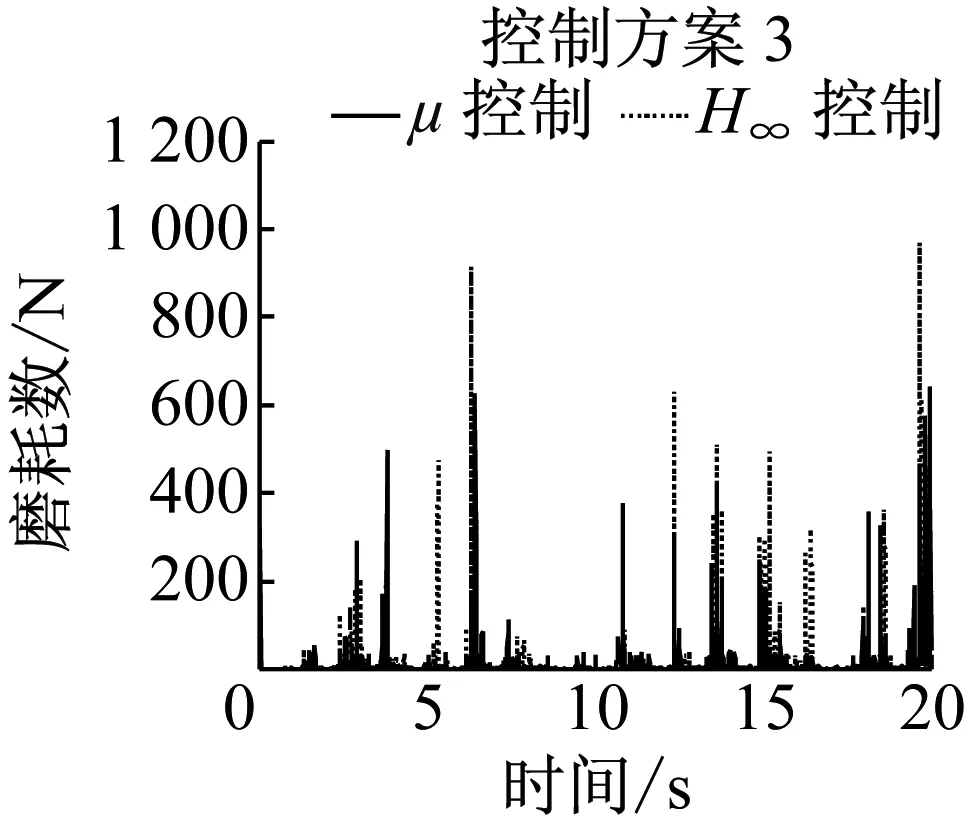
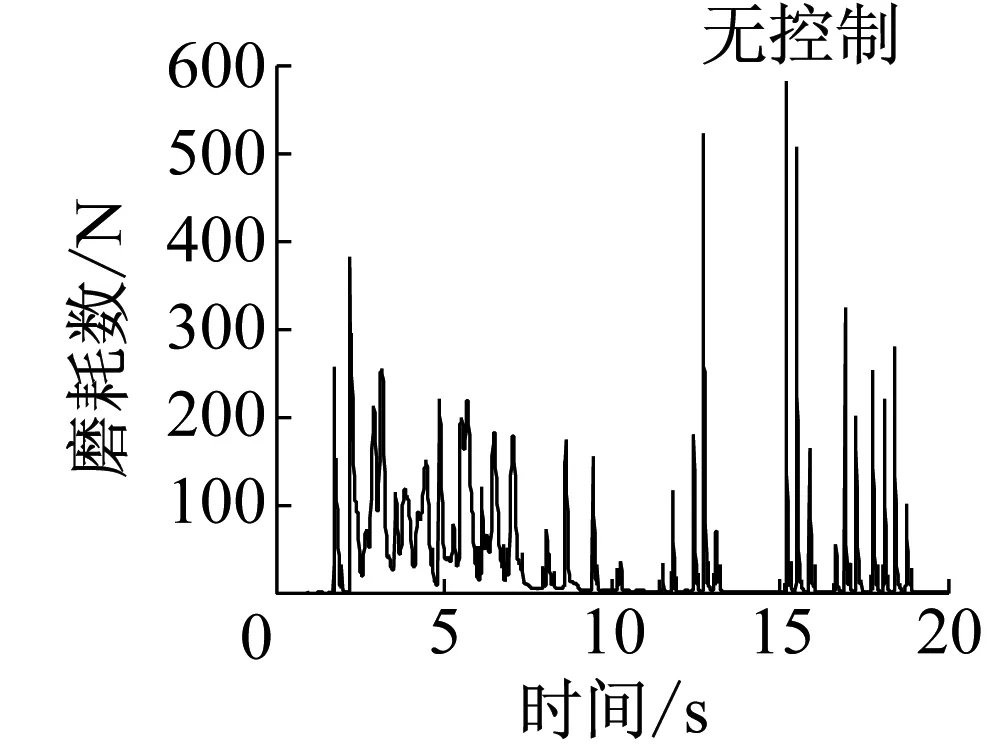
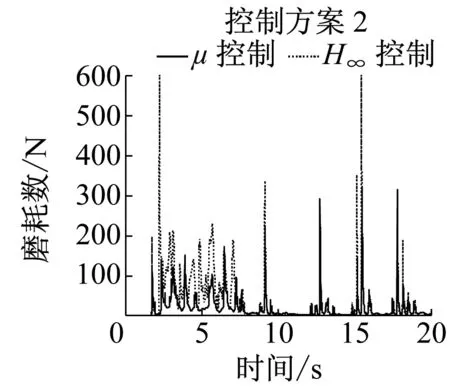
c 磨耗数

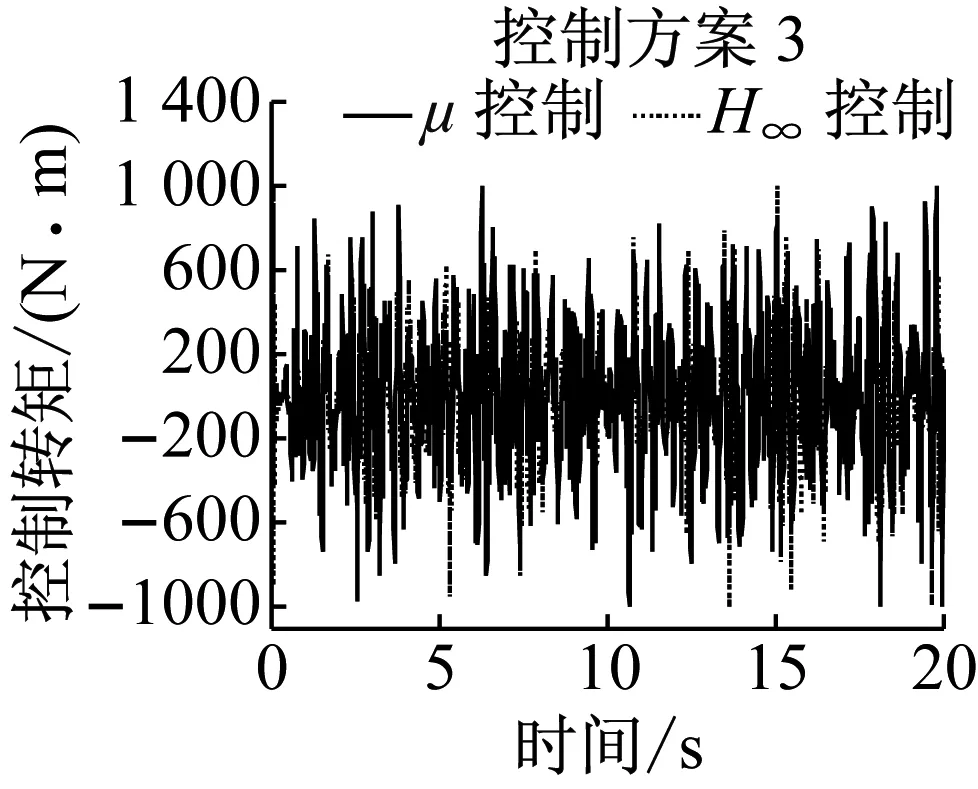
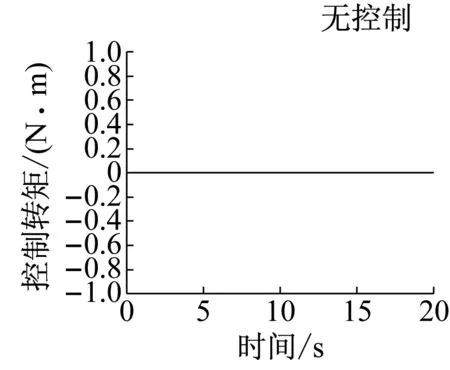
d 控制转矩

图10直线工况仿真结果

Fig.10Simulationresultsonstraighttrack

采用控制方案2和3时，导向轮对的横移量、摇头角、磨耗数及控制转矩见图11，前后轮对横移量和摇头角绝对值的平均值及磨耗数的平均值见表3.可知曲线通过时方案2和3的控制效果完全一致，与控制方案1的控制效果相比，前轮磨耗数均值增加3.4 N，而后轮磨耗数均值降低了6.1 N，即前后轮综合磨耗较方案1降低了2.7 N，与无控制工况相比，前后轮总磨耗数均值由112.1 N降低到51.5 N，综合降幅为54%.

表3 曲线工况控制前后轮对状态

a 横移量

b 摇头角

c 磨耗数

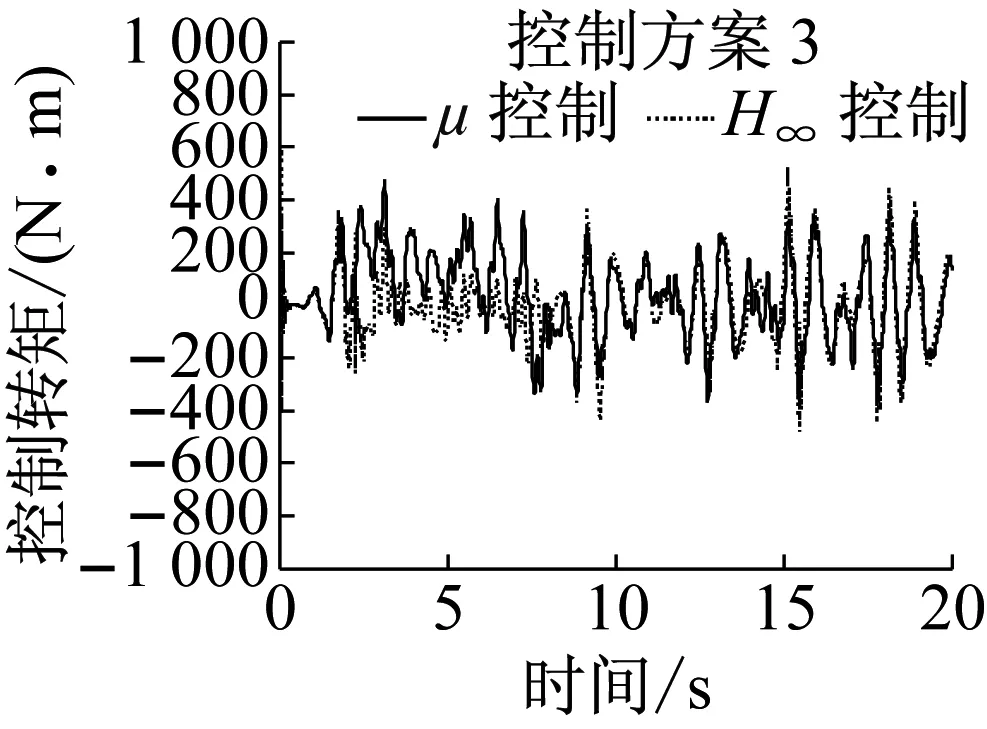
d 控制转矩

图11曲线工况仿真结果

Fig.11Simulationresultsoncurvedtrack

4 结语

研究结果表明：通过控制纵向驱动电机的输出转矩改善纵向耦合驱动独立旋转车轮转向架有轨电车的直线对中和曲线通过性能，并降低车轮磨耗是可行的.采用μ综合鲁棒算法进行控制器设计，可以综合考虑轮轨接触非线性、测量噪声和外部输入不确定性，保证控制器的鲁棒稳定性和鲁棒性能，并可使轮对从车辆模型中独立出来实现本地控制.通过联合仿真对文中提出的3种控制方案进行了对比，表明同时采用前后轮状态作为控制器输入信号时，能得到相对较好的控制效果：在直线和曲线工况时，分别使前后轮综合磨耗数降低38%和54%.