考虑地表边界效应的静压沉桩挤土位移解析

张亚国， 李镜培

(1. 长安大学 建筑工程学院, 陕西 西安 710062； 2. 同济大学 土木工程学院, 上海 200092)

静压桩沉桩过程中产生的挤土效应会对邻近的道路管线、建筑物等产生不利影响.然而，由于沉桩过程涉及到土体的大应变以及非线性变形特性，很难找到一个严格的理论方法对其进行描述.因此，基于一系列简化假设的半解析或经验方法被广泛地应用于工程实践中.

Baligh[1]将土体视为不可压缩的无黏性体，将桩体的贯入过程等效为土体绕桩尖沿流线运动的定常流问题.在不考虑土体本构关系的情况下，沿流线对速度积分求得位移场，进而确定应变场，并导出了沉桩引起的土体应力和孔压的分布规律[2-3].该方法能够反映桩体在土中连续贯入的过程，却无法考虑地表边界效应的影响.

Sagaseta[4]通过源(扩张球孔)-汇(收缩球孔)理论得到了地表面无约束情况下地表面的位移解.Chow等[5]用同样的方法得到了桩周土体的竖向位移场，并用弹性理论法讨论了邻桩的上抬规律，研究参数变化对邻桩上抬的影响.该方法由于能够较好地考虑地表边界效应的影响，不同工况下的沉桩挤土位移研究在此基础上展开[6-7].但源-汇理论是基于线弹性基本假定，难以考虑土体应力与应变之间复杂的本构关系.

假定沉桩挤土过程类似于圆柱孔或球形孔的扩张，圆孔扩张理论被广泛地应用到沉桩挤土效应的理论分析中[8-9].Randolph等[10]将沉桩看作不排水条件下的圆柱孔扩张，分析了沉桩后孔隙水压力的固结消散过程；张亚国等[11]假定土体为理想弹塑性体，基于临界状态扩孔理论求解了沉桩时周围土体中任一点位移.然而上述方法均是基于平面应变假定，没有考虑桩长和地表边界对沉桩过程的影响.

综上可见，寻求一种既能考虑土体本构关系，又能考虑地表边界效应和沉桩深度影响的挤土位移求解方法是十分必要的.本文基于圆孔扩张理论，假定桩周围土体屈服后服从修正剑桥(Modified Cam Clay, MCC)模型，结合静压沉桩特点，首先推导了桩身无限长情况下的初始挤土位移解；进而将已沉入土体的桩身等效为若干个扩张球孔，引入Chai等[12]的修正函数来考虑地表边界和压桩深度的影响；最终得到了便于在实际工程中应用的静压桩挤土位移场理论解.

1 基于平面应变假定的沉桩挤土位移

首先不考虑沉桩时桩长和地表边界的影响，将沉桩过程看作圆柱孔在无限土体中的扩张，即简化为平面应变问题，如图1所示.当不设预钻孔时，初始半径a0=0.受扩孔压力σa的作用，孔壁土体最先出现屈服状态；随着孔压的增大，球孔周围出现塑性区，其半径为rp；圆孔的最终半径为au(即桩半径).假设土体未发生屈服时，呈弹性状态，并服从胡克定律；土体屈服后服从修正剑桥模型.图1中ur,p为柱周任意一点在塑性区内的位移,rp0为弹性边界的初始位置,up为弹性边界的位移.由于压桩速度快，土中孔隙水难以排出，故可将沉桩过程视为不排水过程.

图1 沉桩扩孔的力学模型

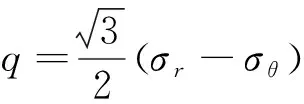
(1)

弹性区桩周围土体中的应力和位移可表示为[9]

(2)

(3)

(4)

式(2)～(4)中:σr,e、σθ,e和ur,e分别为弹性区的径向应力、切向应力和径向位移；σrp为弹塑性边界上的径向应力；rp为弹塑性边界的半径；G为剪切模量.由式(4)可以看出，确定弹性区的位移，首先需要对σrp和rp进行求解.

联立式(1)～(4)，可得到弹塑性边界上应力和位移为

(5)

(6)

(7)

式中：qp为弹塑性边界上的偏应力.

对于rp和qp，则需通过对塑性区的求解得到.在塑性区，土体屈服后服从修正剑桥模型，其屈服函数可以表示为[13]

(8)

(9)

结合式(8)和式(9)可知，在弹塑性边界rp处，偏应力为

(10)

R=αROC

(11)

式中:

将式(11)代入式(10)可得

(12)

受扩孔压力的持续作用，弹塑性边界的位置也在不断地发生变化；然而，弹塑性边界上的应力与该边界所在的位置无关[14].根据式(4)可知

(13)

式中:rx0为孔周某一土单元的初始径向位置；rxp为该土单元刚刚进入塑性状态时的径向位置.

由于扩孔过程可看作不排水过程，周围土体的体应变为零，结合图1有

(14)

式中：rx为土单元目前的径向位置；a为任一时刻圆柱孔半径.

联立式(13)、(14)，并以最终弹塑性边界上的点为研究对象，即令rx、rxp均等于rp，可得

(15)

式中：G0为初始剪切模量.

根据图1中的几何关系，可知

(16)

将rx-rx0=ur,p，rp-rp0=up代入式(16)，并用r代替rx，则塑性区的径向位移可以表示为

(17)

至此，单桩静力压入时引起的扩孔挤土位移已求得:其弹性区(r>rp)的表达式如式(4)所示;塑性区(au≤r≤rp)的表达式如式(17)所示.然而该挤土位移没有考虑地表边界的影响，是假设桩无限长情况下的解，因而需要通过引入函数进行修正.

2 考虑地表边界效应的挤土位移

2.1 修正函数

确定修正函数的基本思路和步骤是：将长为h的桩看作一系列的扩张球孔，通过与镜像位置的虚拟扩张孔叠加得到考虑地表边界影响的弹性挤土位移解[12],如图2所示，该解答与无限长桩体弹性挤土位移解之间的比值即为拟确定的修正函数.假定该函数在桩周土的塑性区仍然适用，则其与平面应变条件下挤土位移弹塑性解的乘积即为最终考虑地表边界效应的沉桩挤土位移弹塑性解.如此，该解答不仅考虑了地表边界效应的影响，还可以考虑土体特性的影响.下面介绍具体的求解过程.

图2 一系列球孔扩张模拟沉桩过程[12]

在MCC模型土中，单个扩张球孔挤土时，有

(18)

(19)

(20)

式中:σrps和ups分别为扩张球孔周围土体弹塑性边界上的径向应力和位移；rps为弹塑性边界处的半径；urs,e为弹性区内的径向位移.

任意埋深处沉桩产生的挤土位移uAx可以通过对一系列扩张球孔及虚拟扩张球孔挤土位移叠加得到

(21)

式中:dr是点A到桩中心的水平距离；s为相邻两球孔球心之间的距离；z为某一球心到点A的竖向距离；u为某一扩张球孔在点A产生的径向位移；h1和h2分别为点A到桩底和桩顶的竖向距离.

当式(20)代入式(21)时，可得到点A位于静压桩的弹性区内时挤土位移，其与圆柱孔弹性挤土位移(式4)比值可作为修正函数f，即

(22)

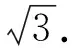
扩张球孔及其对应的镜像扩张球孔叠加后，能够满足地表剪应力为零的条件，正应力为零的条件则不能被严格满足.为此，图3中计算了大小为100 kPa的水平和竖向荷载p分别作用在地表时，1 m远处土体水平方向应变随深度的变化.其中E/p=10，E为弹性模量；泊松比ν为0.3.

图3 不同方向荷载在水平方向产生的应变

由图3可见，在埋深较浅处(0～0.5 m)，水平荷载引起水平方向的应变要远远大于竖向荷载引起的竖向应度.这说明对于土体中侧向位移，地表正应力的影响要远远小于剪应力的影响.由于本文主要研究沉桩侧向挤土位移，因此不再对地表正应力条件作进一步的修正.

2.2 挤土位移的确定

式(21)为积分表达式，尽管式中u根据点A与球心之间的相对位置，可以是弹性或者是塑性位移解，然而塑性解并不满足线性叠加的条件，因此，以弹性区位移的比值f来折减平面应变条件下无限长桩弹性挤土位移(式22)是一种近似的修正方法.修正后的单桩挤土位移可以表示为

u=u1f

(23)

式中:u1为单桩挤土初始位移，当A点位于弹性区时，u1可由式(4)得到；当A点位于塑性区时，u1可由式(17)得到.

3 实例验证

为了验证本文理论分析模型的可靠性，对浙江省秦山核电区静压桩施工过程中的挤土位移进行了计算，并与现场试验结果[15]进行对比分析.现场采用直径为600 mm、桩长为35 m的预应力管桩基础.工程场地20 m深度范围内的土层向下依次是杂填土、粉质黏土、黏质粉土以及淤泥质粉质黏土.假设土体超固结比ROC=1，压缩模量Es=2 MPa，泊松比ν=0.3，其余参数见表1.

表1 土的物理力学参数[15]

当压桩深度为10 m时，距离桩中心3 m远处土体的径向位移沿深度变化如图4a所示.当基于平面应变假定，将沉桩过程简单地看作圆柱孔的扩张时，得到的挤土位移解随着埋深变化并不明显，且在埋深6～10 m范围内明显大于实测值.这是因为该解中假设桩身无限长，没有地表边界效应的影响，而计算过程中又对部分参数进行统一取值，因而不同深度处的挤土位移变化不大.当引入考虑压桩深度和地表边界的修正函数(式22)后，预测的挤土位移与实测值更为接近.图4b为压桩深度为17 m时的挤土位移，修正后的挤土位移与实测值变化趋势较为一致，但在埋深8～12 m处，预测值比实测值小16%左右.

a 压桩深度10 m

b 压桩深度17 m

4 影响因素分析

为了系统地调查静压沉桩过程中的挤土特性，分析了沉桩过程中的预钻孔孔径、桩径以及土体超固结比对距地表2 m，距桩轴线3 m处的土体侧向位移的影响.图5a为埋深2 m处土体挤土位移的变化.由图5a可知，随着到桩中心距离的增大，挤土位移不断减小，当距桩中心距离约为5 m时，挤土位移接近于0；静压桩沉桩挤土影响显著的区域主要集中在距桩1 m范围内.当预钻孔半径a0依次取0、0.1和0.2 m时，挤土位移逐渐减小，且位移减小幅度随预钻孔孔径的增大而增大，如距桩中心1 m处，当a0为0.1 m时，挤土位移较无预钻孔时减小了11.3%，而当a0增大到0.2 m时，挤土位移较a0=0.1 m时减小了38%.

由图5b可知，在距桩3 m远处，侧向挤土位移沿埋深的增加而减小；在埋深6 m以下，位移减幅增大.预钻孔半径a0依次取0、0.1和0.2 m时，可以看到，沉桩挤土位移随着预钻孔的增大逐渐减小，且位移减小幅度随预钻孔孔径的增大而增大.如在埋深2 m处，当a0为0.1 m时，挤土位移较无预钻孔时减小了10.9%；而当a0增大到0.2 m时，挤土位移较a0=0.1 m时减小了37.4%.

a 挤土位移随径向距离的变化

b 挤土位移随埋深的变化

土体径向位移与桩径的关系如图6所示.其中，图6a和6b分别反映的是固定埋深和固定径向位置处土体侧向位移随沉桩过程的变化.由图6可知，随着桩径au的增大，径向挤土位移逐渐增大.桩径等值增大时，挤土位移并非线性增大.例如，在图5b中，当桩径au从0.2 m增加到0.3 m时，埋深2 m处的挤土位移增加了7.2 mm；而当au从0.3 m增加到0.4 m时，该处的挤土位移增加了10.1 mm.

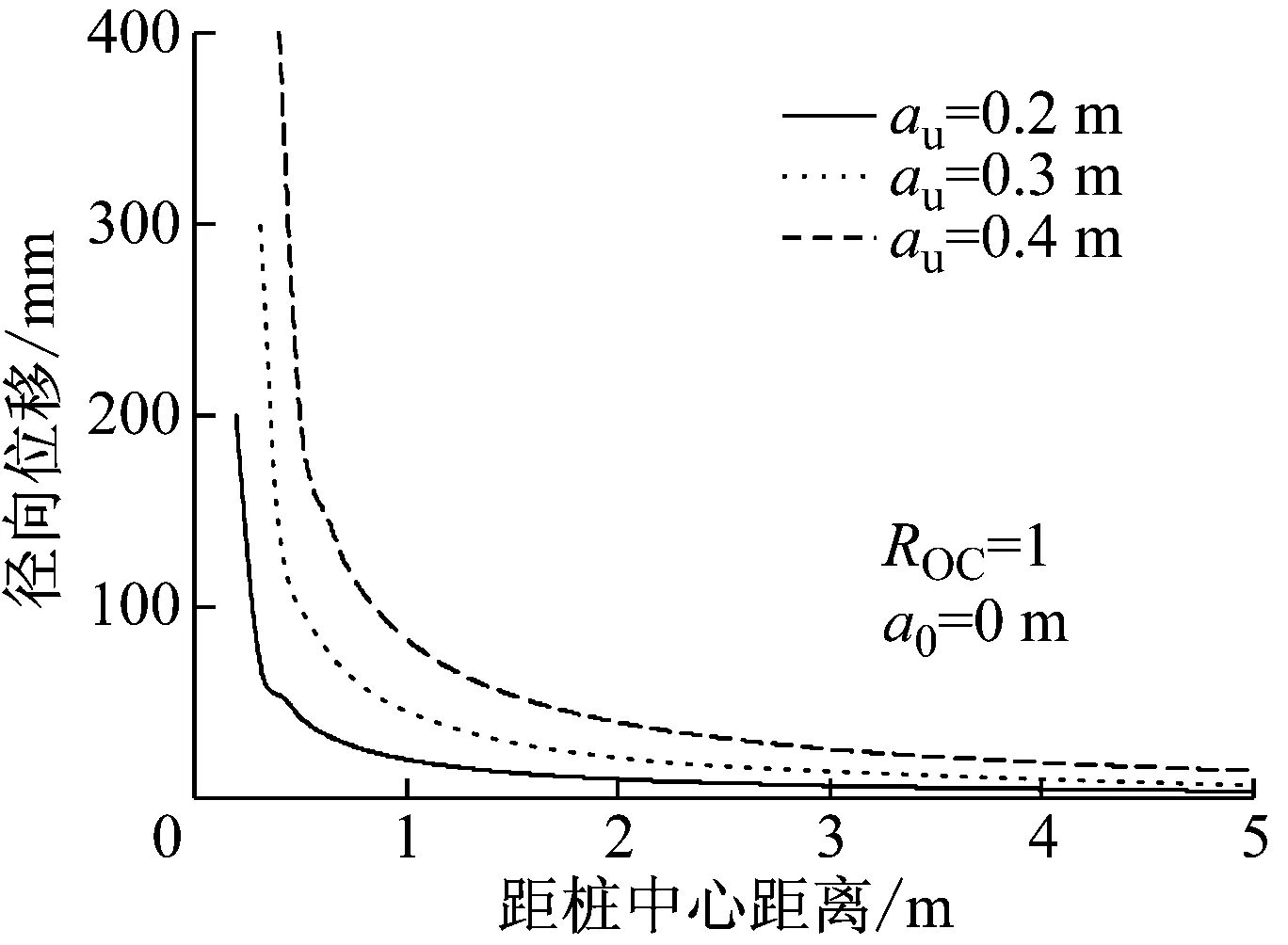
a 挤土位移随径向距离的变化

b 挤土位移随埋深的变化

取不同ROC时，沉桩径向挤土位移如图7所示.由图7a和7b可见，随着ROC的增大，挤土位移有所增加.这是因为与正常固结土相比，超固结土的密实度高，土颗粒之间的空隙小，排列紧密；因而，对于距桩同样距离的土颗粒而言，超固结状态下，其受到的挤压作用较明显，位移也略大.

本文所提的模型由于考虑了地表边界效应的影响，较无限体假定情况下能更好地预测沉桩挤土位移.但需要指出的是，由于该模型中采用的土体本构关系是基于重塑土提出，在分析现场沉桩问题时还存在一定的局限性.这是因为天然黏土大多具有结构性，蒋明镜等[16]研究指出天然结构性黏土具有独特的力学性质.因此，利用本文模型预测天然土中沉桩挤土位移时仍存在一定的偏差，这也一定程度上解释了图4中理论预测值与实测结果仍存在较大差异的原因.图8中将陈文等[17]的沉桩挤土(重塑黏土)离心模型试验结果与本文计算结果进行了对比，结果显示本文方法在预测重塑土中的沉桩挤土问题更为准确.

a 挤土位移随径向距离的变化

b 挤土位移随埋深的变化

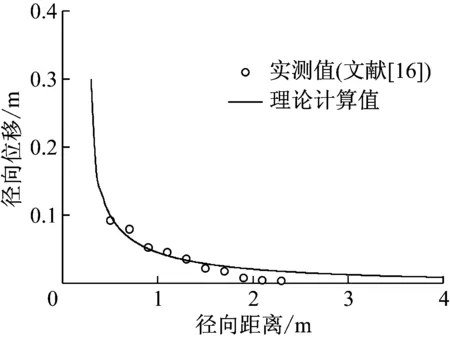
图8 计算结果与重塑土中实测值的比较

5 结论

(1) 本文基于圆柱孔在修正剑桥模型土中的扩张理论推导了静压桩的初始挤土位移解，通过引入近似的修正函数来考虑地表边界效应以及沉桩深度的影响，与文献实测结果的对比验证了本文方法的可靠性.由于该方法提出的挤土位移表述式形式简洁、物理意义明确，易于在实际工程应用.

(2) 计算分析表明，随着预钻孔孔径的增大，沉桩挤土位移非线性减小；随着桩径的增大，挤土位移呈非线性增大；当土体超固结比增大时，挤土位移也略有增长，这是由于超固结土颗粒排列紧密，受到的挤压作用明显所致.

(3) 本文通过设置镜像扩张球孔来考虑地表边界的影响，适用于估算沉桩挤土引起的径向位移；对于沉桩时地表发生的竖向位移场分布，将在后续工作中进一步研究.