长三角地区区域经济发展的实证分析

矫卫红

（烟台大学 经济管理学院，山东 烟台 264000）

0 引言

从经济发展的角度来看，一个区域的经济发展既受其所处区位的影响，又影响着其相邻区域的发展。地区资源的要素、人文社会条件基础、经济发展模式、区域内市场的发展状况都制约了区域经济的发展。区域经济增长可以促使地区产生明显的集聚效应，出现城市化集聚、产业集聚，刺激城市化规模扩大，经济增长迅速。我国地域辽阔,自然条件、地理环境、历史文化背景差异大,地区间经济发展不平衡，为实现区域经济协调发展，掌握区域经济的发展情况十分必要。从空间计量经济学角度研究经济发展情况可以为今后经济增长提供参考。

国内外对于经济发展理论的研究颇多，大多数学者是采用空间计量模型研究相关经济问题[1-4]。因此，本文从地理加权空间经济计量模型的角度出发，通过运用地理加权空间经济计量模型的DMM框架进行数据推导，研究区域经济的发展情况，为进一步促进区域经济发展提出针对性意见。

1 区域概况

区域经济是指在一定区域内内部因素与外部条件相互作用而产生的生产经济综合体[5]，以区域为界限，经济要素与空间分布相结合的发展实体。

长三角地区是我国最大的经济区，也是重要的经济命脉。该地区总面积占全国陆地总面积的2%，人口占有率是全国总人口的11%，国内生产总值占全国GDP的20%。长三角区域经济主要发展外向型经济，对外贸易发展较快，外贸贡献较高；引进外资的规模较大，随着该地区市场、产业、区域的比较优势，大批外商投资企业进入该地区，逐渐拉动经济圈的经济转型，由资源型向投资驱动型转变；经济发展迅速，生产的国际化程度较高，已成为我国具有经济发展水平高、综合竞争力强、城镇化水平最为完善的发达地区[6]。

长三角区域的经济发展绝不是孤立的，该地区与横向的中西部经济区，以及纵向的京津冀和珠三角城市群都有着千丝万缕的联系。中西部地区为长三角地区提供了丰富的资源与广阔的市场，长三角区域经济对中西部经济发展具有带动和辐射作用，而京津冀和珠三角城市群的高速发展也成为推动长三角保持发展的动力引擎。所以，对长三角区域经济的发展研究具有重要的现实意义。

2 地理加权空间经济计量模型的构建

为研究地理加权空间经济计量模型，本文从空间统计方法与空间计量经济模型的基础上阐述模型的假设可靠性，从而验证模型的正确性。

地理加权空间经济计量（Spatial Geographically Weighted Regression SGWR）模型，是通过研究空间相关性与异质性二者之间关系形成的，主要分成两部分[7]。一部分是地理加权空间误差（GWR-SEA）模型，另一部分是地理加权空间滞后（GWR-SL）模型。本文总结前人的研究成果，从模型理论的根本出发，创新性地利用地理加权空间经济计量模型在经济发展中的应用进行分析，探索经济发展与空间区域的相关性。

2.1 模型准备

根据空间计量经济的基本理论，在基本地理加权回归模型的基础上对空间相关性与差异性模型进行分析，现有回归模型：

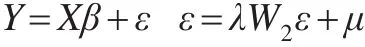
式中，μ~N(0，Ω)的定义为A=I-ρW1，B=I-λW2,W1和W2代表n×n表示空间权重矩阵（标准化或者未标准化的），与其对应的变量在空间自回归的过程中可与矩阵不同，从而生成不同的空间结构。

2.2 模型检验

利用Moran’s I检验方法检验模型的空间相关性，用公式表示为：

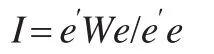
式中，e代表回归模型的残差估计值。

对Moran's I值的近似值期望值E(I)和方差V(I)的分布状况计算如下:

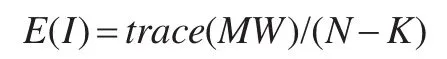
2.3 模型建立

建立地理加权空间经济计量模型的误差模型，在观测点i(i=1，2，3，...，n)的任意取点处得到的回归面的近似值用线性形式表示为：

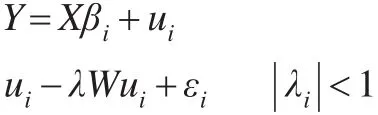
式中，X、Y表示解释变量矩阵与变量矩阵，W表示对角线0的空间权重矩阵，(ui，vi)表示观测点为i的地理观测坐标，空间误差系数用λi=λ(ui，vi)表示，系数向量用

由此得到标准化形式：时，当测点i(i=1，2，...，n)发生变化时，模型的系数变为δi=(δ1，δ2，...，δn)T。由此可知，δ表示不同于空间误差模型的，表示n×p型矩阵的系数向量。

本文运用Gauss地理矩阵：

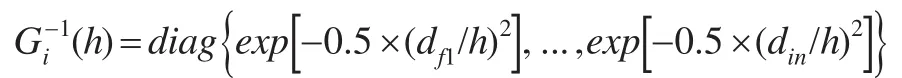
其中，dio代表欧式距离，是观测点o与i的距离，h(h＞0)代表窗宽。矩阵(h)与Y=Xβi+ui，ui-λWui+εi，|λi|＜1的乘积得到:

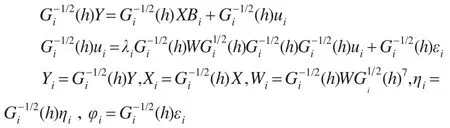
同时，也可以用下列式子表示：

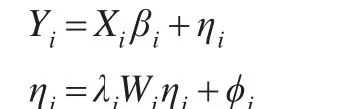
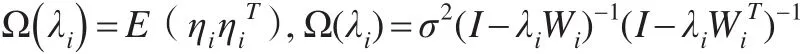
3 实证分析

3.1 数据来源

本文以长三角地区为研究对象，以国家批准的行政区域划分为准，包含上海市、浙江省以及江苏省的地级市，选取2001—2017年为研究时间段。数据选取以《浙江省统计年鉴》《上海市统计年鉴》以及《江苏省统计年鉴》所记载的数据为准，并利用各个地级市的统计年鉴作为补充。

3.2 变量选取

根据影响我国区域经济的影响因素的指标体系制定出调查问卷。调查的对象包括从事金融事业的专业人员、接触金融的业务人员、经济金融参与者等，人员分布均匀。共发放调查问卷400份，收回有效问卷385份，回收率为96.25%，符合统计的要求，研究的结果具有普遍性、可靠性和专业性。经过归纳总结，得到影响因素如下：

（1）整体GDP经济增长率。人均国内生产总值比例作为区域生产总值和劳动力总数之间的比例，是衡量区域经济发展水平的重要指标。本文将长江GDP经济增长率作为整体的GDP经济增长率为因变量进行研究。

（2）相邻区域GDP增长率。相邻区域GDP增长率指的是研究区域相比邻的区域的GDP经济增长率，本文研究的相邻区域的GDP增长率指的是长江区域周边省份的GDP经济增长率。

（3）初始经济状态。初始经济状态指的是区域经济发展研究最初的状态，是根据时间所表述的经济状态，也是对经济后期研究的一个起始设定。

（4）地理空间误差。地理空间误差指的是不同区域、地域和地区等条件下，对区域经济的影响。因此，本文是在长江区域经济研究的基础上，进行的相近地区的研究。

综上，本文将整体GDP的经济增长率作为衡量区域经济的因变量，把相邻区域内的GDP增长率、初始经济状态与地理空间误差作为自变量。

3.3 初始模型估计结果

本文根据现有模型，得到相关变量和系数如表1所示，并将其带入到区域经济的模型中，进行下一步的研究。

表1 模型估计

3.4 空间依赖性分析

长三角地区金融发展空间经济计量模型的估计结果如表2所示。由表2可知，系数β的估计值在模型中呈现负数，说明长三角地区的经济增长率与经济条件呈负相关，也就是说落后地区的经济发展在开始阶段处于较快的经济增长率，逐渐追上经济发达地区并且二者逐渐趋于平衡；空间滞后的显著性在显著检验之后，对被解释变量的影响是显著的，也就是说，相邻区域内的GDP增长率、初始经济状态、地理空间误差与长三角地区的GDP增长率都有明显影响。模型中解释变量与GDP经济状态有明显影响，初始经济状态的空间滞后性与GDP的经济增长率呈现正相关，由此说明长三角地区的初始经济状态与区域经济增长明显相关，即有空间依赖性。

表2 长三角地区金融发展空间经济计量模型的估计结果

3.5 相关性检验

长三角地区金融股发展的空间相关性检验显示正相关性，因此对模型的回归残差进行空间相关性检验是十分必要的，表3给出了模型的估计结果与检验值。

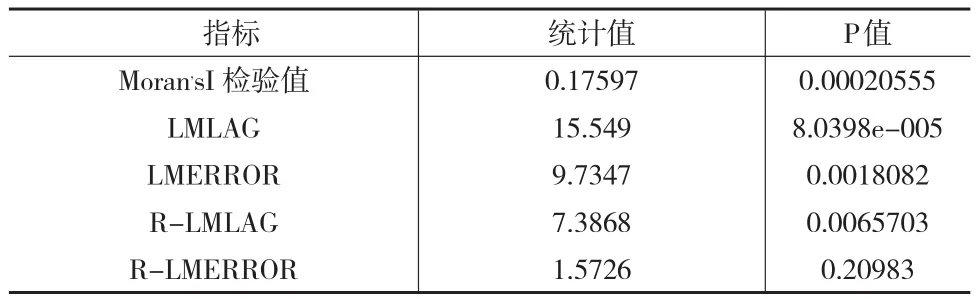
表3 空间相关性检验与模型选择

根据表3所示，残差中Moran，s I的数值显示为0.00020555，那么在显著性水平上空间的相关性检验可以顺利通过，表明模型的相关性检验与模型的选择有很大关联，表3表达了明显的回归残差在空间上的分布情况，可知残差的分布特点呈空间聚集模式。为此，采用地理加权空间经济计量模型消除长三角地区之间的空间正相关性。

3.6 具体指标分析

结合本文现有的因变量和自变量进行分析，得到结果如表4所示。

表4 区域经济发展实证研究

由表4可知，长江区域经济与相邻区域内的GDP增长率关系系数为0.3541，即长江区域经济与相邻区域内的GDP增长率之间的关系为正相关，长江区域经济会随着相邻区域内GDP增长率的提高而提高；长江区域经济与初始经济状态关系系数为0.4589，即长江区域经济与初始经济状态之间的关系为正相关，长江区域经济会随着初始经济状态的提高而提高；长江区域经济与地理空间误差关系系数为-0.1870，即长江区域经济与相邻区域内的GDP增长率之间的关系为负相关，长江区域经济会随着地理空间误差的提高而降低。

4 结论与建议

本文提出了地理加权回归经济计量模型，利用长三角地区的金融发展数据进行模型估计和检验，验证了模型的正确性，证实了区域经济发展对于空间相关性的依赖。长三角地区在空间上，相邻区域内的GDP增长率、初始经济状态、地理空间误差与长三角地区的GDP增长率都有明显影响。初始经济状态的空间滞后性与GDP的经济增长率呈现正相关，由此说明长三角地区的初始经济状态与区域经济增长呈现明显空间依赖性。为此，本文提出建议：增加长三角地区间的科技交流，利用相邻区域的技术互补性，建立技术合作共享机制进而推进区域技术的多层次交流，提升地区技术总量水平；增加区域之间的贸易往来，应充分利用本地区的资源优势，完善临近省份的经济活动往来，同时利用好区域内优势资本外溢性，吸纳优势企业来本地发展；提高地区企业的综合竞争力，不断提高人力资源的整体水平，充分发挥FDI外溢的显著性作用，重视企业文化素质的培养，关注新型科技创新，跟上创新企业的步伐；提升区域资本使用效率，进一步完善基础设施建设，保护好资源环境，积极响应“绿水青山就是金山银山”的口号响应，在发展经济的同时重视资源环境的保护，充分利用临近省份资源外溢效应，促进本区域的经济稳定增长。