相对误差对相关系数影响的统计特性

丁 勇

（南京医科大学康达学院 理学部，江苏 连云港 222000）

0 引言

相关和回归是统计学研究的重要内容。在实际工作中，受各种因素的影响，原始数据不可避免地存在一定的误差，这些误差对计算的结果会产生一定的干扰，因此需要对误差的影响进行分析和研究。查阅文献发现，关注误差对回归分析影响的研究非常多，例如经典的最小二乘法、最小一乘法都是针对误差对回归的影响[1-5]；而关注误差对相关分析影响的研究则很少[6，7]。

相关系数是研究变量之间相关程度的重要指标，在理论研究和实际工作中得到了大量的应用[1,2,8]，例如，相关系数作为变量之间的距离，在多元统计分析中，广泛应用于聚类分析、主成分分析等。因此，研究数据误差对相关系数的影响有重要意义。本文在一个变量有相对误差的情况下，探讨相对误差对简单相关系数（又称pearson积差相关系数，以下简称相关系数）的影响。

1 公式与性质

1.1 公式推导

记 r 为 x=(x1，x2，…，xn)和 y=(y1，y2，…，yn)的相关系数，则[1，2]：

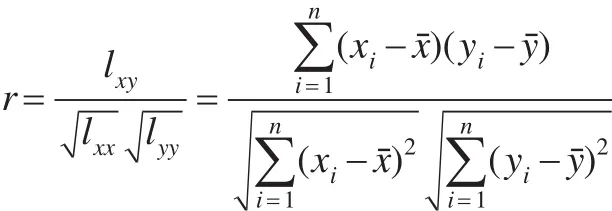
考虑x、y两个变量其中之一有误差，由于对称性，不妨设 y有相对误差：；这里εi~N(0，σ2) 且相互独立。记 ε=(ε1，ε2，…， εn) ，则由样本标准差和总体标准差的关系可知：

从而可以把σ近似看成是y的平均相对误差（以下简称相对误差）。

记r*为x=(x1，x2，…，xn)和的相关系数，则：

由此可知，r*是由ε确定的随机变量，上式比较复杂。为了较简单明了地分析相对误差对相关系数的影响，本文从总体特性的角度进行分析。从理论上获悉r*的统计分布再推导总体均数E(r*)比较困难，为简单起见，考虑如下的近似公式：

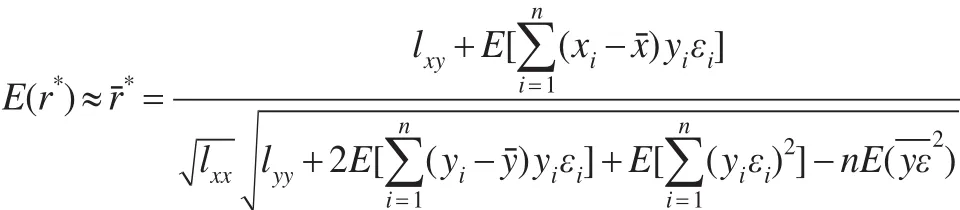
由 数 理 统 计 知 识 可 知[1]：E(εi)=0 ，E(εiεj)=E(εi)E(εj)=0(i≠j) ，且，所 以，从 而，故有。这里E(X)为随机变量X的数学期望，χ2(1)为自由度为1的卡方分布。由数学期望的 性 质 可 知[1]E[(xi-ˉ)yiεi]=(xi-ˉ)yiE(εi)=0 ，E[(yi-ˉ)，又因为，所以从而，因此：

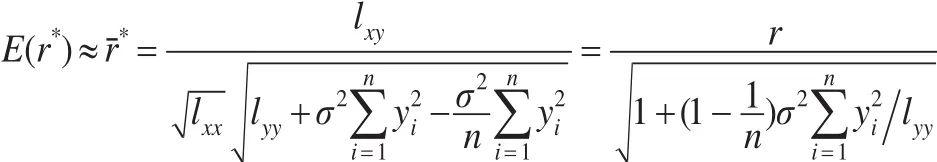
式（1）为有相对误差数据的相关系数的总体均数的近似公式，与数据有相对误差相对应，考虑相关系数的相对总体均数：

当ˉ=0，且σ2较小时，式（2）为：

当n≥2、σ≤20%时：

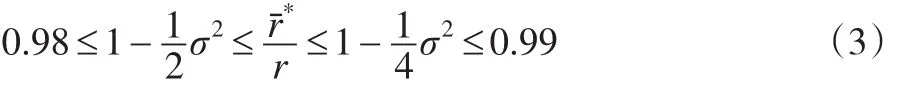
1.2 误差对相关系数影响的统计特性

由式（2）可得如下相对误差对相关系数的影响的3个统计特性：

性质2：相对误差σ值越小，对相关系数的影响也越小；当σ=0 时，|=|r|；

性质3：相对与性质1误差对相关系数的影响和有误差数据的二阶原点矩与二阶中心矩的比值有关，其值越小，影响越小；因为，故当yˉ=0 时，，此时，y的大小对相关系数没有影响。

2 模拟研究

2.1 数据

式（1）、式（2）是近似公式，其精度如何？由近似公式得到的性质是否和实际情况相符？下面通过一组数据进行计算机模拟考察和验证。在实际应用中，考虑到相对误差不会太大，故设相对误差界为20%。

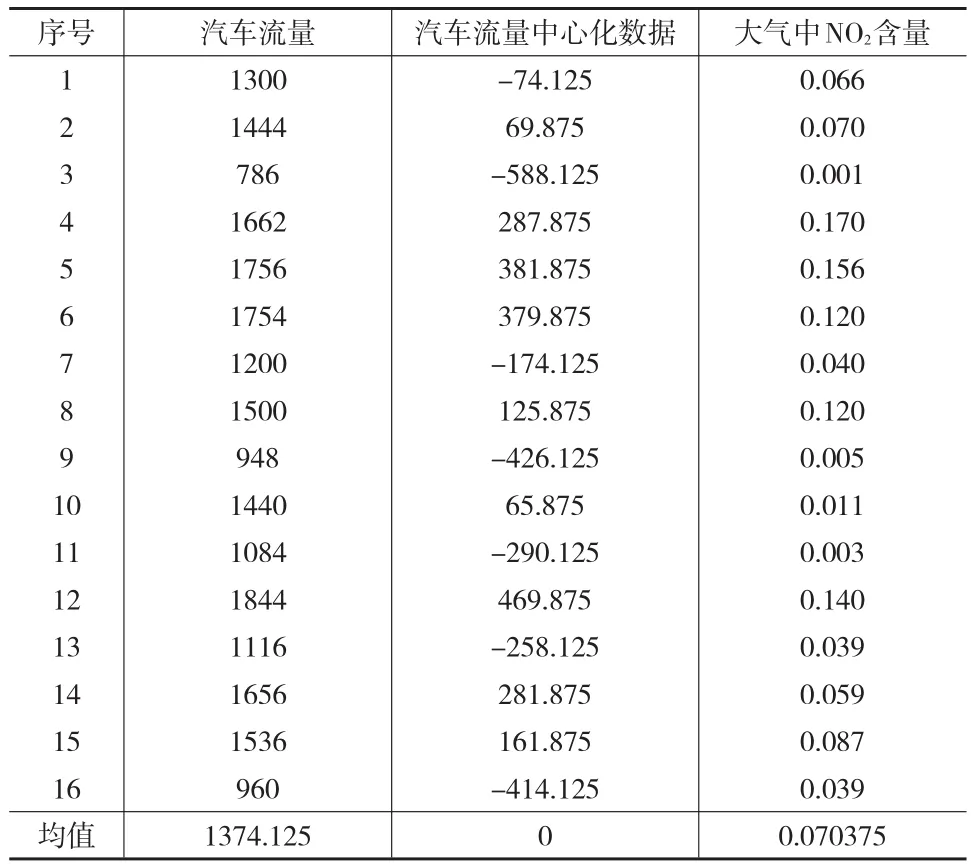
表1 某交通点大气污染情况的测定数据

表1是某交通点大气污染情况的16个测定数据[9]，第1列为汽车流量（辆/小时）数据，第3列为大气中NO2含量（毫克/立方米）数据，这两者的相关系数为r=0.8304，第2列为汽车流量减去它的平均值得到的中心化数据,由数理统计知识可知，两个变量或其中之一做线性变换时，它们的相关系数不变[1]，所以它与大气中NO2含量（毫克/立方米）数据的相关系数也为r=0.8304。由于本例的相关系数大于0，故在以下的讨论中，省去相关系数的绝对值。

2.2 模拟研究

本文将汽车流量作为x，大气中NO2含量作为y，此时取相对误差σ分别为0.05、0.10、0.15和0.20（表2第1列），再由εi~N(0，σ2)产生有相对误差的随机数，分别进行了10000次模拟，得到10000个x和y*的相关系数r*，统计其中r*＞r的个数（表2第2列，记为m），计算r*的均值和标准差（表2第4列）以及r*与r比值的均数与标准差（表2第7列），为便于和近似公式比较，表2第3列和第6列给出了公式（1）和公式（2）的结果。

表2 大气中NO2含量数据有相对误差时10000次模拟结果

显然，当没有误差时，r*=r，从而=r*=r，式（2）也表明，当相对误差σ为0时，=r；当数据有相对误差时，由式（2）可知，要小于r，表2第3列结果验证了这一点，＜r=0.8304 ，且当σ增大时，变得更小。是r*的平均值，＜r的一个可能原因是当相对误差σ存在时，r*＞r的个数会减少，表2第2列的结果验证了这一点。以上结果与前述的性质1和性质2的结论是一致的。

为比较y值的影响，取大气中NO2含量数据为x，汽车流量数据为y，此时=19.7638，比表2的要大的多。类似上述的模拟方法，可得表3的各模拟结果。表3第2列与表2第2列栏类似，随着误差σ增大，r*＞r的个数越来越少，相比表2的个数还要少；表3第3列与表2第3列栏类似，随着误差σ增大而变小，相比表2的数值还要小。

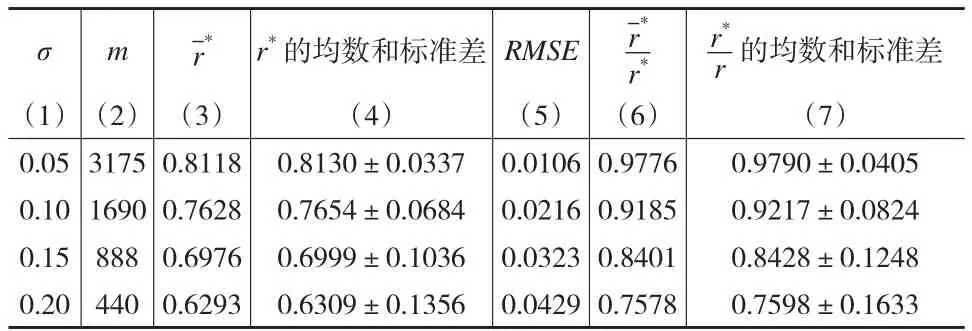
表3 汽车流量数据有相对误差时10000次模拟结果

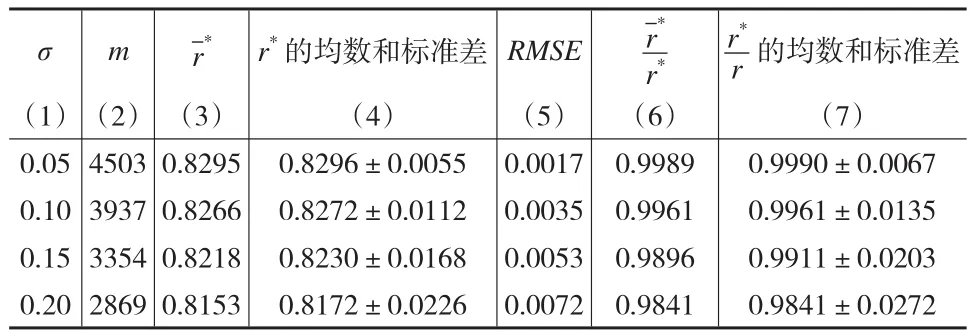
表4 汽车流量中心化数据有相对误差时10000次模拟结果

图1

2.3 近似公式的精度

由表2、表3和表4的第3列、第4列和第6列、第7列可知，与r*的均数的均数都比较接近，且标准差较小，说明近似公式有较好的精度，本文进一步以均方根误差（root-mean-square error）为精度评价的量化标准，由于与仅差一个常数，为简便起见，只对进行比较，记显然，当σ=0 时，r*=r，从而=r，所以此时RMSE=0 ；另外4种σ的情况，计算机模拟的计算结果列于表2、表3和表4中第5列，一个有趣的现象是，RMSE与σ成正比关系（下页图2，图中R2为决定系数），表4的RMSE小于σ的3.6%（图2中☆数据），表2的RMSE小于σ的6%（图2中*数据），表3的RMSE小于σ的21.5%（图2中o数据）的值越小，RMSE与σ比值就越小；三种情况都表明，RMSE远远小于误差σ，这进一步说明近似公式有较高的精度。由于的精度与的精度是一致的。由于近似公式有较好的精度，由此得到的3个性质与实际情况相符也就顺理成章了。与仅相差一个常数，因此

图2 均方根误差RMSE与相对误差σ的关系图

3 讨论

从复杂的现象中，排除次要因素的干扰，梳理出重要线索，抓住主要矛盾，有助于分析事物间的本质联系。本文从总体特性的统计规律出发，利用简单的近似公式，较好地找到了相对误差对相关系数影响的主要因素。

从变量数据散点图的几何直观来看，数据点越分布在回归直线附近，变量的相关性越好。众所周知，数据的误差会对相关系数产生影响。一般来说，当误差使数据点靠近（远离）回归直线时，相关系数会增加（减少）。由于误差是随机的，因此，误差有可能使相关系数（绝对值）增加，也可能使相关系数（绝对值）减少。本文研究表明，从统计规律来看，误差的影响大多数情况是不利的，会使变量的相关性变差。

对于相对误差，一般会认为数据变量的绝对值越大，误差会越大，从而对相关系数的影响也越大。本文研究得到一个重要的结论是：数据的二阶原点矩的与二阶中心矩的比值对相关系数有较大的影响。误差会对相关系数产生影响，但仅有误差，影响的作用并不大，公式（3）说明了这一点，误差和二阶矩比值的共同作用，特别是二阶矩的比值较大时，会对相关系数产生较大的影响，图1给出了直观的说明。数据均值为0时，二阶矩的比值达到最小值1，此时数据大小对相关系数没有影响。因此，数据相对误差对相关系数的影响，除了误差和数据的大小，还要考虑数据是否对称分布、均值为0。在实际问题中，可以把二阶矩的比值作为一个评价指标，当该指标数值较小时，相关系数的值比较稳定，受误差的影响较小。