纵流换热器的换热性能及计算

马石磊

(上海电气电站设备有限公司电站辅机厂，上海 200090)

0 概 述

在纵流壳程换热器中，管束具有新型的支撑结构，可使壳程流体由传统的横向流动改变为纵向流动，因而强化了壳程传热。纵流壳程换热器具有高效节能的特点，已广泛应用于化工、动力及轻工等行业。在20世纪70年代，美国某石油公司首先开发了纵流壳程折流杆换热器，管束的核心部件是折流栅，主要由折流杆、折流圈、交叉支撑条、分程隔板和纵向滑杆组成。根据折流杆布置位置的不同，折流栅可分为横栅和纵栅，以某角度交错排列，对换热管进行固定，折流杆的直径与相邻两换热管的间隙几乎相等[1]。自20世纪80年代以来，国内郑州大学、华中科技大学和华南理工大学也开展了纵流壳程换热器的研究，对壳程的折流支撑结构进行了优化，并广泛投入了工业应用[1]。

1 纵流壳程换热器

纵流壳程换热器具有消除管子振动、改善壳程流动、降低壳程阻力、增强管束刚性、便于清理、减轻结垢和提高传热效率等一系列优点，应用前景广阔。该类换热器适用于壳程高雷诺数或层流状态下的传热，也适用于壳程介质为黏性流体的传热。主要应用场合为：(1)天然气领域中的气气换热。因为是纵流形式，在流量和流速较高的工况下，可防止管子振动。(2)天然气冷却器。纵流可使壳程流动均匀化，降低了压降，节省能耗。(3)用于各种冷凝器，可改善壳程流动状态，提高冷凝效率。(4)废热锅炉。可以减轻结垢和延长使用周期。(5)釜式或虹吸式重沸器，用以增强其可靠性和减轻设备重量[2]。因为换热器内流体的流动和传热过程十分复杂，所以，对换热器的研究和开发，主要还是通过制作模型测得所需的数据，以获得换热器流体传热和流动阻力的经验或半经验的无因次准数关联式。现以某电站工程项目中的换热器为研究对象，对纵流试验样机的壳程流动进行仿真计算，提出了壳程传热和流动性能准数关联式，并结合试验参数，对该关联式进行了校核，为纵流换热器的热工计算，提供参考。

目前，大多数纵流换热器管束的支撑结构多为折流杆型，圆柱形折流杆的结构，如图1所示。在设计纵流换热器时，若采用圆柱形折流杆，将造成布管节距偏大，在壳程流量相同的情况下，壳程流体的流速偏低，壳程的传热膜系数也会相应降低。鉴于此，换热器的壳程折流支撑，可采用钢条替代圆柱形折流杆，既可减小壳程布管间距，还可增强管束支撑强度。现研究的纵流换热器管束折流支掌结构即为该种栅条式结构，管束外围设置折流圈来实现栅条的定位。

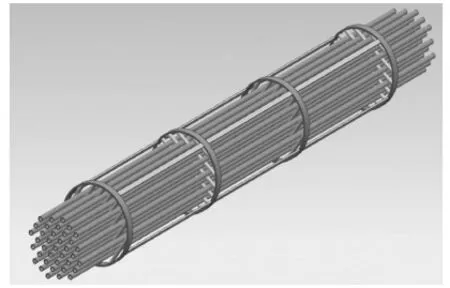
图1 圆柱形折流杆的结构

2 壳程的换热系数

折流杆换热器与传统的折流板换热器在管程传热性能上的差别不大，但在壳程上，折流杆换热器用折流栅取代了折流板，将壳程流体由错流变为纵向流动。由2根折流杆和2根换热管包围形成每个单元流道，这样的流道截面形状决定了其后方流体的延展趋势。高速流体横向通过折流杆时，在折流杆表面形成边界层，随着雷诺数的增加，产生边界层分离，在折流杆两侧发生漩涡脱离，形成涡街，如图2所示。由于漩涡迅速形成，逐步分裂，并最终消失，从而增加了流体的湍流程度，强化了壳程传热。在折流杆换热器的整个壳程内，流体沿着管束方向作纵向平行流动，壳程内部没有传热死区，整个管束的传热表面都得到有效利用，虽然内部每一点的传热速率要低于弓形折流板换热器内的横流区，但传热表面的有效利用弥补了这一点。壳程流体的流动在充分延展后，在经过每个折流圈时，都会在其后方形成周期发展的涡街，同时，由于折流圈交错排布，涡街的分布也交错变化，涡街不断发展和交替变化使管子外表面的边界层减薄、脱离或完全消失，边界层不能持久地稳定，使管侧和壳侧之间传递热量的阻力减小，强化了传热，且纵向流提高了传热面积的有效利用率，在流速较高的情况下，相比与传统的折流板换热器，折流杆换热器具有更高的壳程传热系数。

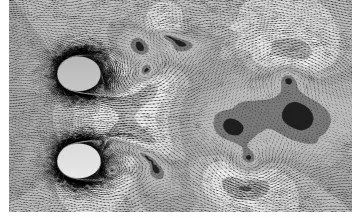
图2 流体绕过折流杆时的状态

折流杆换热器是典型的纵流壳程换热器，从首创至今，对壳程传热系数方面的计算，具有多种多样的计算关联式。现列举几种典型计算关联式，为后续研究作参考[1]。

2.1 郑州大学热能工程研究中心的计算关联式

在研究传热性能时，通常将影响因素归纳成几个无因次特征数，然后将折流杆换热器壳程传热系数，表示为这些特征数的关联式。计算关联式为：

Nu=AhRea1Pra2(Lb/de)a3(Lt/Di)a4(μ/μw)a5

(1)

在式(1)中：Nu—努塞尔数，Nu=αde/λ；

Re—雷诺数，Re=deusρ/μ；

Pr—普朗特数，Pr=cpμ/λ；

Lb—折流栅间距；

de—壳程当量直径；

Lt/Di—管束长径比；

μ—流体在主体温度下的黏度；

μw—流体在壁面温度下的黏度；

Ah—系数；

a1，a2，a3，a4，a5—待定指数。

2.2 美国某石油公司的计算关联式

(1)层流流动

(2)湍流流动

(3)系数的计算

在层流和湍流情况下的几何系数CL、CT，根据管束几何函数Cl、Ct、入口效应参数ξl、ξt、以及管子表面函数Csl和Cst进行定义。

CL=CslClξl

CT=CstCtξt

管束几何函数Cl、Ct，是折流圈间距Lb和管束泄露面积与壳程流通面积之比Al/As的指数函数。

层流时：

Cl=Ct0+(Ct0-Ct∞)exp(-0.00615)Lb

Ct∞=0.182-0.172λ

Ct0-Ct∞=0.120-0.533λ

湍流时：

Ct=Ct∞+(Ct0-Ct∞)exp(-0.00496)Lb

Ct∞=0.042-0.0417λ

Ct0-Ct∞=0.023-0.0117λ

折算变量λ的定义式为：

λ=[(Al/As)+0.1]0.5

壳程流通面积As、折流栅流通面积Ab以及泄露面积Al为：

(2)

(3)

(4)

在式(2)～式(4)中：Ds—壳体直径，m；

Dt—管外径，m；

Do—管束外层管子的布管圆直径，m；

Dbo—折流圈外径，m；

Dbi—折流圈内径，m；

nt—管子数量；

Lr—管长，m。

2.3 华南理工大学化机所的计算关联式

(1)层流流动

(5)

(2)湍流流动

(6)

在式(5)～式(6)中：

Gi，G4—流道结构几何因子，与折流杆换热器的几何尺寸有关；

Cd—流体阻力系数；

φ—摩擦阻力系数；

ro—流道当量半径；

Pr—普朗特数；

Prt—湍流普朗特数；

K1,K2,K3,Z—系数。

2.4 华中科技大学的计算关联式

(1)Re<3600时

Nu=fwNu1

(7)

在式(7)中：

fw=f1f2f3

(8)

f2=1-(Ab/As)+0.85837(Ab/As)-0.031

(9)

f3=1+0.1138exp[-0.01022(Lb/Dbo-1)2]

(10)

在式(8)～式(10)中：

As—壳程最大流通截面积，m2；

Ab—壳程最小流通截面积，m2；

Dbo—折流圈外径，m；

Lb—折流圈间距，m；

nb—折流圈数目；

μ—流体在主体壁温下的黏度；

μw—流体在壁面温度下黏度。

(2)Re≥3600时

Nu=ΦwNu2

(11)

在式(11)中：

Φw=Φ1Φ2Φ3

Φ2=0.96-0.062(0.1+Ab/As)0.6

Φ3=0.4951+1.2488[-0.01659(Lb/dbo-1)2.5]

2.5 预测某型换热器的计算关联式

综合考虑上述折流杆式的纵流壳程换热器换热公式后，并对照换热器设计手册中所列的Donohue法[3]，得到某型栅条式纵流换热器的壳程换热系数计算关联式为：

(12)

在式(12)中：A0、A1、A3、A4—待定系数；

Lb—折流圈间距，m；

ds—壳程当量直径。

3 壳程的换热性能及试验

为了验证栅条式纵流换热器壳程换热系数的准确性，制造了相应的纵流壳程试验样机，欲通过试验进行验证。试验样机的折流支撑与布管形式均与原型机相同，试验时，样机和系统测点的布置，如图3所示。换热性能试验包括了汽水换热试验及水水换热试验，壳程流体为蒸汽时，Re约为20 000～90 000。壳程流体为水时，Re约为11 000～70 000。壳程Re的取值范围，均覆盖实际产品的工况参数。

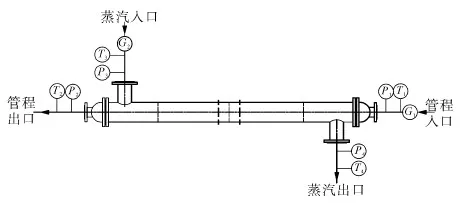
图3换热性能试验样机和系统测点布置

经汽水和水水换热试验后，获得了栅条式纵流换热器换热性能的试验数据，并与拟合公式的计算结果进行了对比，结果显示二者匹配程度较好，可为该型纵流换热器的设计和计算，提供参考。

4 结 语

通过汇总，列出了传统圆柱形折流杆换热器的计算关联式，并结合相关标准中Donohue公式，提出了适用于栅条式纵流换热器的计算关联式。

针对某型换热器原型，设计并制造了相应的试验样机，经汽水换热试验和水水换热试验后，获得了相关数据，并拟合了壳程换热的计算关联式。通过对比和验证，试验所得数据与拟合后关联式的计算结果相当吻合，表明拟合后的计算关联式，可用于栅条式纵流壳程换热器的设计和计算。