先张法预应力波型板桩截面分析与力学试验

黄建华，朱永涛，覃少杰，常建华

(1.福建工程学院 土木工程学院 福建 福州350118; 2.地下工程福建高校重点实验室 福建 福州350118)

预应力混凝土板桩作为一种新生的预制混凝土直立式挡土支护结构，在土地资源日益紧缺的城市区域内的河道整治工程、市政管道工程、基坑支护工程的建设中可以极大程度的减少征地面积，降低对周边环境的影响[1-3]。由于独特的结构截面设计使其在力学性能、挡土止水等方面具有一定优势，因此得到了广泛的应用。近些年来，随着建筑行业的不断进步，混凝土板桩的制造工艺不断提升，其截面形式也由单一的矩形截面发展到方形薄壁、工字形薄壁等形式[4-5]。

当前，在水利、港口、码头等工程领域中常见的挡土结构主要有普通混凝土平板桩、钻孔灌注桩以及地下连续墙等传统的支护方式。此类支护结构的共同特点为需现场施工浇筑混凝土，从而导致施工周期变长，工程成本提高。而预制混凝土板桩可以很好地解决现浇混凝土支挡结构现有的缺点。先张法预应力波型板桩(以下简称“波型板桩”)作为一种新型挡土支护用预制混凝土板桩，相对于传统的混凝土支护桩具有结构挡土截面大、抗弯抗剪强度高、施工工期短、经济生态效益显著等优点[6-7]，是一项绿色节能工程技术产品，对河岸驳堤、边坡基坑等工程应用技术有重要意义。

1 波型板桩截面设计

1.1 板桩截面形式

在水利边坡与基坑支护工程中，要求支护结构不但要满足挡土要求，还要具有止水功效。波型板桩截面设计形式可以同时发挥挡土与止水作用，截面形式借鉴了钢板桩的力学性能优越性和材料制作的经济性。结合混凝土板桩截面形式与河岸、边坡工程的支护挡水要求，新型预应力波形板桩的截面形式如图1所示，截面设计利用槽榫搭接的方式实现桩与桩之间的搭接，并发挥其止水作用[8]。

图1 预应力波型板桩截面简图

1.2 截面有效预压应力计算

混凝土的弹性变形、徐变、收缩以及预应力钢筋的松弛是混凝土波形板桩截面有效预压应力的主要影响因素。此外，张拉锚具的变形和钢筋内缩、混凝土蒸汽养护、预应力钢筋的应力松弛以及混凝土收缩和徐变同样会引起预应力钢筋预应力的损失[9]。一般来说，当分析所得的预应力总损失值小于100 MPa时，取100 MPa。桩身混凝土有效预压应力σce具体可以参考《混凝土结构设计规范》(GB50010-2010)中有关混凝土有效预压应力值的方法进行分析[10]。

2 波形板桩力学性能计算

2.1 桩身抗裂弯矩计算

根据《混凝土结构设计规范》(GB50010-2010)波型板桩抗裂弯矩Mcr按式(1)计算：

Mcr=(σce+γ·ftk)·W0

(1)

式中：Mcr为波形板桩桩身抗裂弯矩, kN·m；σce为波形板桩桩身截面混凝土有效预压应力, MPa；ftk为桩身混凝土抗拉强度标准值, N/mm2；γ为混凝土截面抵抗矩塑性影响系数；W0为板桩换算截面受拉边缘的弹性抵抗矩, mm4。

2.2 桩身正截面抗弯承载力计算

波型板桩采用预应力结构，在保证构件结构强度的同时降低了构件的结构配筋率[11-12]。取桩身正截面受弯承载力计算示意图如图2，本文以截面高度为450 mm和600 mm的桩型作为主要研究对象，进行力学性能分析。

图2 波型板桩受弯承载力计算示意图

由于波型板桩顶板位于受压区内，故受压区高度的不同会引起受压区截面形式的变化如图3。

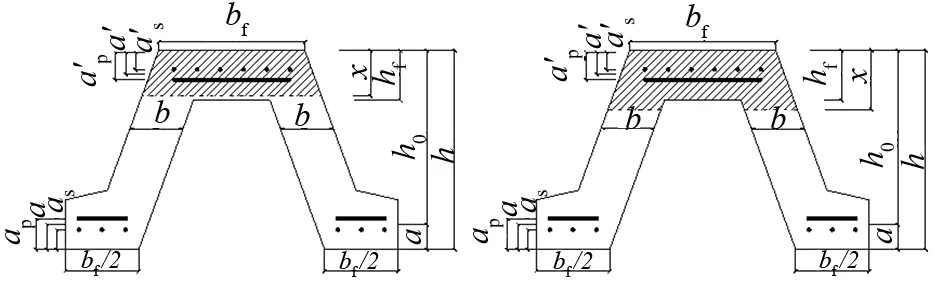
图3 波型板桩受压区高度

①若符合式(2)的条件，按高度为x的梯形截面分析。

fpyAp+fyAs

(2)

②若不符合式(2)的条件，其正截面的受弯承载力按下列公式计算。

根据力矩平衡条件可知：

M

(3)

根据水平方向力的平衡条件可得：

fpyAp+fyAs=α1fc[Ac1+b(x-hf)]+

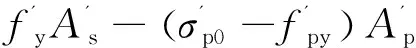
(4)

适用条件为：

xξbh0

(5)

x≥2a'

(6)

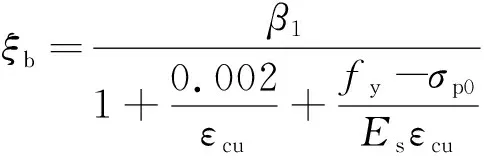
(7)

如果x2a'，可近似按以下方法计算。

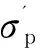
M

(8)

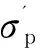
M

(9)

2.3 桩身抗剪承载力计算

当配有箍筋时，波型板桩斜截面的抗剪承载力Qp应按《混凝土结构设计规范》(GB50010-2010)第6.3.4条的规定计算：

Qp=Vcs+Vp

(10)

式中：Qp为波形板桩斜截面抗剪承载力设计值, kN；Vcs为预应力波形板桩斜截面混凝土和横向钢筋抗剪承载力设计值, kN；VP为由预应力所增加的部件抗剪承载力设计值, kN。

(11)

Vp=0.05Np0

(12)

式中：λ为计算截面的剪跨比，取l=1.5；fyv为横向钢筋抗拉强度设计值, N/mm2；Asv为横向钢筋的截面面积, mm2；S为沿长度方向的横向钢筋间距, mm；Np0为计算截面上混凝土法向预应力等于零时纵向钢筋的合力, N；σp0为预应力钢筋合力点处混凝土法向应力等于零时的预应力钢筋应力, N/mm2。

2.4 计算实例

依据上文理论计算公式，计算不同截面高度波型板桩的力学性能，构件采用C60高性能混凝土，纵向受力钢筋采用直径为15.2 mm的预应力钢绞线，其中顶板与底板预应力钢绞线的数量相同，箍筋按照规范要求配置1Φ8@200。为与试验形成对比，理论计算时波型板桩原材料的力学性能均采用标准值。各详细参数及计算过程见表1、表2。

表1 波型板桩截面尺寸及配筋情况表

续表1

表2 波型板桩力学性能分析表

3 载荷试验与分析

3.1 抗弯试验

采用简支梁对称加载装置对波型板桩进行抗弯试验分析，如图4所示，其中竖向荷载F的方向垂直于地面(波型板桩的轴线与地表平行)。抗弯试验用的波型板桩要求截面高度为450 mm单节桩长不得小于6 m，截面高度为600 mm，单节桩长不得小于7 m，且最大桩长均不超过15 m。本实验中采用截面高度450 mm的AB+型波型板桩进行抗弯试验，桩长为12 m。

注：1分配梁铰支座垫板；2分配梁固定铰支座；3分配梁；4分配梁滚动铰支座；5波型板桩；6滚动铰支座；7支墩铰支座垫板；8支墩；9固定铰支座；10、11、12测挠度用百分表。

图4波型板桩抗弯试验示意图

Fig.4Bendingtestofacorrugatedsheetpile

(1)加载程序

第一步：根据抗裂弯矩的大小以20%的差值，由0逐级加载至抗裂弯矩的80%，每级荷载的持续时间180 s；然后再以抗裂弯矩的10%为差值，由80%逐级加载至100%。每级荷载的持续时间180 s，观察是否有裂缝出现，测量并记录各项读数。

第二步：若加载至抗裂弯矩的100%时，桩身没出现裂缝，则以抗裂弯矩5%的差值继续加载至桩身出现裂缝。每级荷载弯矩的持续时间依然180 s，观察并记录出现裂缝时荷载大小及裂缝宽度。

第三步：按极限弯矩5%的级差继续加载，构件达到极限状态的标志有以下3种：桩身受拉区范围内裂缝宽度达到1.5 mm；受拉钢筋被拉断；受压区混凝土破坏；出现以上任一现象时，观察并记录出现裂缝时荷载大小及裂缝宽度。

(2)弯矩计算公式

垂直向下加载：

(13)

垂直向上加载：

(14)

水平加载：

(15)

式中：M为抗弯弯矩；G为波形板桩重量；L为波形板桩长度；F为试验荷载值；a为1/2的加荷跨距，长度为0.5 m。

(3)抗裂荷载和极限荷载的确定

抗裂荷载的取值方法如表3所示，极限荷载的取值方法如表4所示。

表3 抗裂荷载的取值方法

表4 极限荷载的取值方法

3.2 抗剪试验

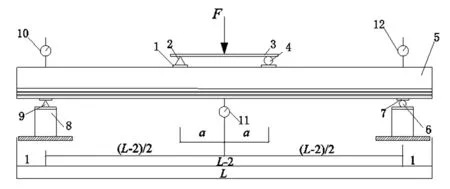
利用对称加载装置进行波型板桩的抗剪试验，如图5，其中，F垂直于地面方向，剪跨b取2.0H，试件悬出长度L1取(2.0～3.0)H。L试验用波型板桩长度；1/2a的加荷跨距，长度0.5 m；

注：1分配梁支点；2分配梁；3波型板桩；4铰支座；5支墩；

图5波型板桩抗剪试验示意图

Fig.5Shearingtestofacorrugatedsheetpile

(1)加载程序

第一步：根据抗剪承载力设计值以20%的差

值，由0逐级加载至剪力设计值的80%，每级荷载的持续时间为180 s；然后再以剪力设计值的10%为差值，逐级加载至100%。每级荷载的持续时间保持180 s，观察是否有裂缝出现，测定并记录各项读数。

第二步：若加载至剪力设计值的100%时桩身没有出现裂缝，则以剪力设计值的5%为差值继续加载至桩身出现裂缝。每级荷载弯矩的持续时间依然为180 s，观察并记录出现裂缝时荷载大小及裂缝宽度。

(2)抗剪承载力计算公式

实测抗剪承载力按下式计算：

(16)

式中：Q为抗剪承载力；F为剪跨内产生斜拉裂纹时的荷载。

(3)抗剪承载力的确定

抗剪承载力的取值方法如表5所示。

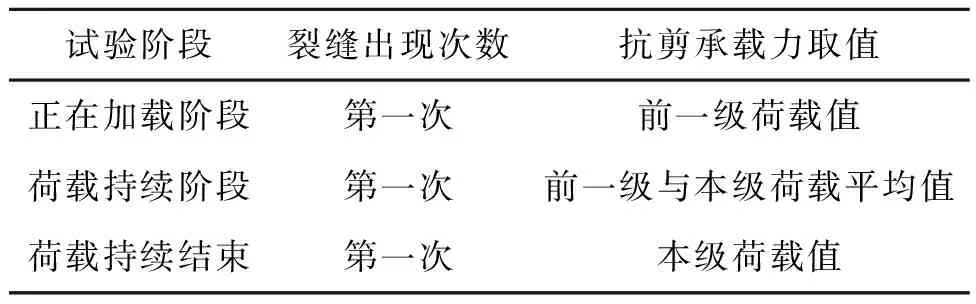
表5 抗剪承载力的取值方法

3.3 试验结果分析

以截面高度450 mm的AB+型波型板桩为实例，表6列出了此种桩型的抗裂弯矩、抗剪承载力、极限弯矩理论值、实验值以及二者比值。通过分析计算，抗裂弯矩实验值与理论值的比值为1.21，抗剪承载力实验值与理论值的比值为1.06，极限弯矩实验值与理论值的比值为1.14。由此可见，理论计算方法可真实反映波型板桩的抗剪承载力和极限弯矩；此外，抗裂弯矩理论计算值与实测值相比偏小，工程上利用理论值作为设计值可能偏于保守。

表6 力学试验与理论计算结果分析

4 结论

1)直接利用波型板桩原截面形式特点，给出截面有效预压应力的确定方法，推导波型板桩截面力学性能分析的理论计算公式，并通过力学试验证明。相对于以往等效截面计算方法，新方法计算过程简单明了，计算结果更加科学合理，可为波型板桩的设计提供理论依据，便于实际工程项目的应用推广。

2)新型波型板桩特殊的截面结构形式不仅提高了挡土截面宽度，而且有效提高了截面高度与截面惯性矩，使得板桩受力性能得到显著提升，经济效益明显，是一种更为合理的挡土止水围护桩型。

3)通过波型板桩抗弯试验与抗剪试验的操作实施与计算分析，给出了波形板桩抗裂弯矩、抗剪承载力的确定方法，并将理论分析与试验值进行对比，结果基本吻合,证明计算方法合理可行。

4)本研究仅针对单根波形板桩进行力学性能分析与试验验证，实际工程应用中，波形板桩挡土止水过程形成排桩联合受力，桩间土所产生的“拱效应”对板桩受力形态的影响尚需进一步深入研究。