嵌入式网络电子信息系统鲁棒性优化计算方法

潘晓贝

（三门峡职业技术学院，河南 三门峡 472000）

一、前言

在网络操作平台当中，其主要的系统就是嵌入式网络电子信息系统，对该系统在异常的输入环境与压力环境下衡量其能否正常工作，主要需要度量其鲁棒性，实现鲁棒性的优化，能够有效提高系统运行的安全性和精确性。因此，结合相应系统特点，针对性地提出鲁棒性优化计算方法具有重要意义。

二、嵌入式网络电子信息系统

嵌入式网络电子信息系统在实际生活当中具有广泛的应用，比如学校的嵌入式网络电子监考系统（图1），通过该系统建立现代化智能监考环境，该技术对推动社会进步具有重要意义。要实现科学合理地设计嵌入式网络电子信息系统，就要结合其鲁棒性的相应约束，对嵌入式网络电子信息系统其结构特点实现全面细致的分析，并以此实现系统相关鲁棒性的确定，并在此基础上，有效地对嵌入式网络电子信息系统当中各种影响鲁棒性的因素进行准确的计算。在设计和计算当中，和嵌入式网络电子信息系统相应鲁棒性存在易行相关联系的参数包括：

（一）获得鲁棒性相应近似值

将嵌入式网络电子信息系统其失效因素类型设定为G，将每一种因素实际对鲁棒性影响的概率设定为Pi（i=1，2，…，G），将嵌入式网络电子信息系统其鲁棒性近似值设定为R，那么对于R的计算则可通过以下公式实现：

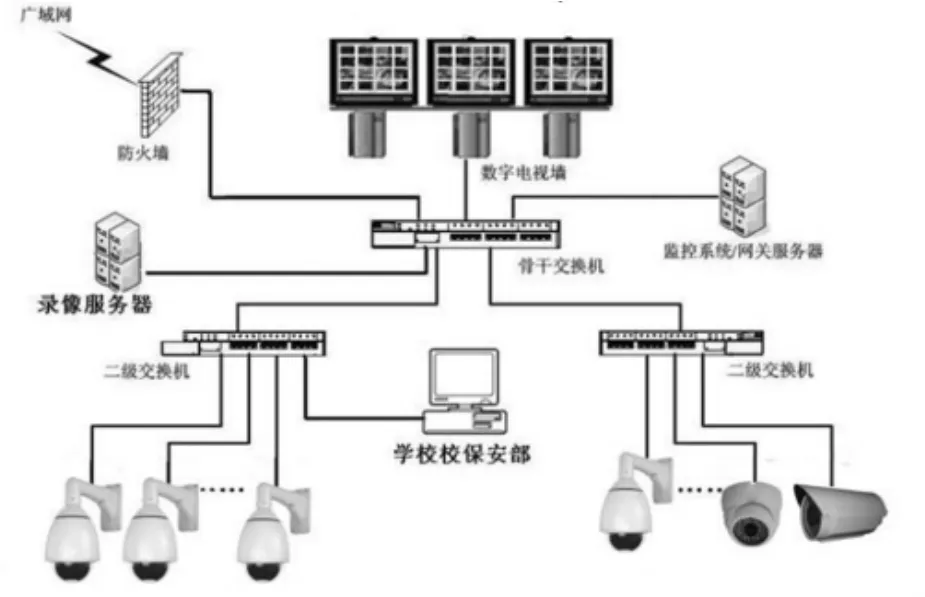
图1 嵌入式网络电子监考系统网络连接示意图

（二）指标和鲁棒性近似值之间的转换

将嵌入式网络电子信息系统其鲁棒性指标设定为βs，在每一个影响鲁棒性的因素都是服从于正态分布的时候，R和βs要实现有效的转换，可以通过公式 R=Φ（βs）实现，在公式当中，Φ（βs）表示的是设计嵌入式网络电子信息系统在鲁棒性相应约束条件之下符合标准形式的正态分布相应函数。在获得上述公式之后，在鲁棒性的束缚之下，利用分布函数就能设计嵌入式网络电子信息系统，不过此时依然有鲁棒性差相应问题存在，设计当中要进行一步采取有效措施以实现鲁棒性的优化设计[1]。

三、嵌入式网络电子信息系统的鲁棒性优化设计

（一）嵌入式网络电子信息系统失效概率计算

在系统设计的时候，在获取相应分布函数之后，要针对相应的系统实现分析自身结构特点，同时将系统其失效模式进行分类，主要按照状态分为两种，一种是单一极限状态，另一种是多极限状态。在不同状态类型下要相应的计算出系统实际失效的概率，并在实现失效概率获取之后，得出嵌入式网络电子信息系统其鲁棒性实现优化需要的相关功能函数。实际当中，针对失效模式主要分为两类，一类是多极限状态，另一类是单一极限状态，而不同的状态也根据变量的差异进行确定。如果系统在失效模式当中，各种失效因素属于串联的关系，同时每个失效的因素内部所含有的变量都具有一定的共同性，则此失效模式就属于单一极限状态；当其中一失效因素当中包括变量因素时，那么就是出于多极限状态当中的失效模式[2]。

针对系统进行失效概率的计算，实际上就是针对该系统结构相应安全事件的交集或者实现失效事件的概率相关计算。实际的计算步骤可以按照下面的方法进行：

1、针对系统在其单一极限状态下计算相应失效概率。随机向量在其含有一些不确定的参数时，设置其向量为 X=[X1，X2，…，Xn]r，要实现在单一极限状态下失效概率的计算，可以通过以下公式进行具体的计算：

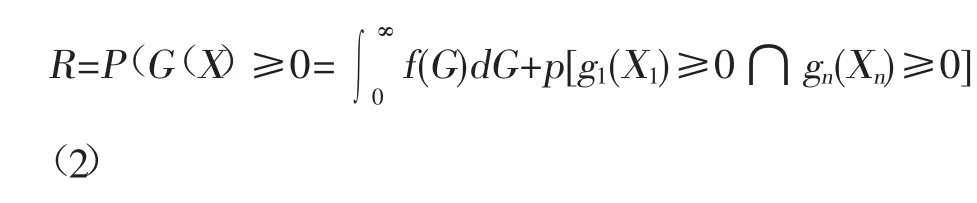
公式当中的g1(X1)表示的是此模式下相应失效函数；dG表示因为系统突然出现了故障，引发系统失效存在的概率；f（G）表示因为系统当中内部的组成元件自身质量有问题，引发系统失效存在的概率；gn(Xn)表示导致系统失效的各种因素之间存在串联关系；p表示保障系统信息的能力系数；G(X)表示导致系统发生失效的各种因素之间的实际比例。

2、在多极限状态下实现对系统计算其失效概率。将对应的失效模式之下其失效函数设置为g（x），同时 g=[11,12,21,22…mn…ln]，要实现对多极限状态下相应失效概率的计算，可以通过以下公式进行：

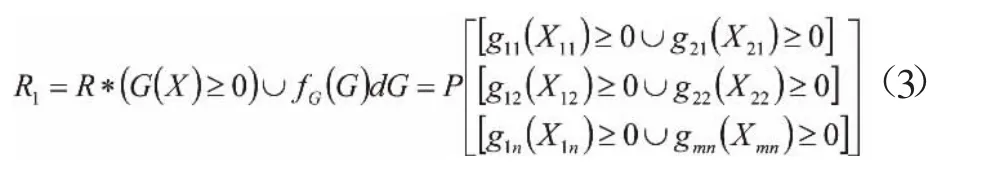
3、计算系统其鲁棒性优化的目标函数。要实现相应目标函数的确定，就要以计算出来的失效概率作为基础。针对系统当中的失效变量，可以将当中n个独立的变量设定为x1，x2，xn，如果这些变量其母体一样，并且分布规律也是一样的，相应方差与均值也是存在一致性，那么设定其均值为μ，方差为σ2，随机的失效事件为A，则A实际发生概率则由P（A）表示，并且在n次的实验当中，将失效事件发生的实际频数设定为m，则失效事件实际的发生频率可以表示为W（A）=m/n，因此，可以通过以下公式对系统其鲁棒性优化相应目标函数进行有效的计算：

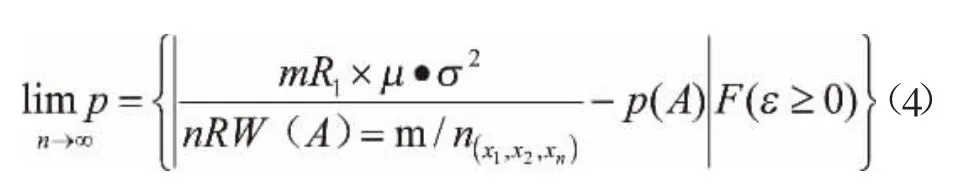
（二）嵌入式网络电子信息系统的鲁棒性优化设计

在得出嵌入式网络电子信息系统鲁棒性优化的目标函数基础上，把粒子群优化和混沌优化进行有机的融合，并将结合成果加入到相应算法中，并在优化过程中获取的功能函数利用之下，对系统的鲁棒性优化相关区域实现动态搜索，在实现系统相应鲁棒性实际改进的目标函数利用科学方法实现计算后，在一定范围之内寻找最优。具体可按照以下次序进行：

1、对嵌入式网络电子信息系统其鲁棒性的优化目标相应函数值进行计算。根据系统相应鲁棒性的功能函数，动态地对系统的鲁棒性相应优化区域实现有效搜索，以对相应目标函数值实现科学的计算。可通过以下两公式进行表示：

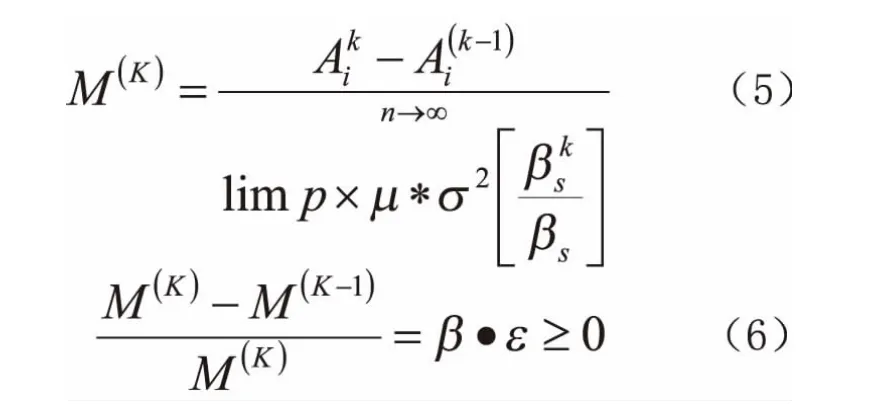
公式当中M(K)表示系统鲁棒性的改进目标相应函数值表示系统对鲁棒性的容许指标表示系统其鲁棒性改进当中涉及到的正态分布相关函数；β·ε≥0表示的是针对鲁棒性其优化区域所进行的动态搜索范围表示相应上限；M(k-1)表示系统其目标的函数值实际取值区间[4]。

2、利用科学的方法计算系统其鲁棒性改进优化当中对应的目标函数值，得出相应结果之后，对更新粒子相应位置和速度实现有效计算。针对更新粒子相应速度与位置可以通过以下公式进行表达：

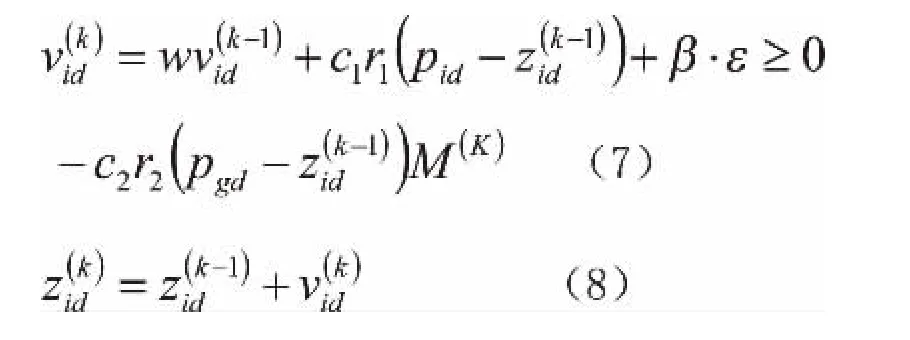
利用混沌因子进行科学的判断，在系统结构为基础分析相应鲁棒性，并计算其中每一个粒子，以分析其是否与相应的约束条件相符合，若符合，那么粒子λ＝0，如果不符合，那么粒子λ=1。要实现粒子值的获取，可以通过以下公式实现：

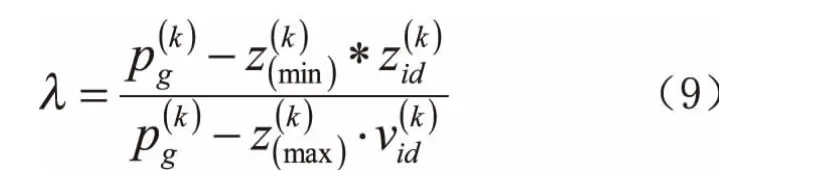
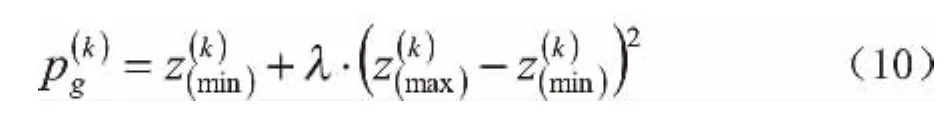
5、通过公式（10）获得的粒子群相应最优位置，在对目前情况下实现更新，如果与预算的迭代次数或者运算精度相符合，那么就可以停止搜索，将结果输出，若不相符，则进行下一个步骤：

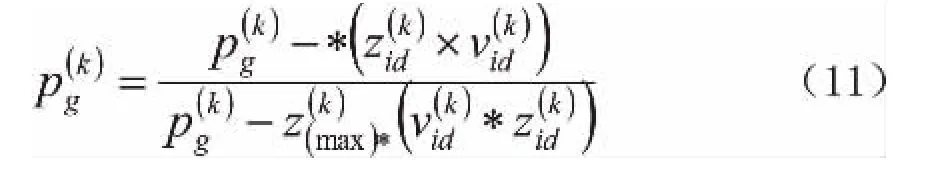
6、在优化设计嵌入式网络电子信息系统相应鲁棒性的过程中，在实现科学搜索之后，空间内如果产生随意群体要有百分之八十剩余的时候，就回到第三步序列中重新进行。

通过上述步骤，在对嵌入式网络电子信息系统进行鲁棒性优化当中，通过优化原理，能够有效地实现优化设计[5]。

四、实验和仿真证明

根据上面提到的关于将混沌粒子群算法进行有效改进之后，以此为基础得出的嵌入式网络电子信息系统相应鲁棒性相应优化方法，需要针对其理论进行以此实际的实验，并通过试验对方法有效性进行科学的验证。在仿真实验中以MATLAB7.0实现对嵌入式网络电子信息系统相应鲁棒性的仿真平台进行有效搭建。当优化模型与参数取值相应条件都一致的情况下，通过改进算法实现系统相应鲁棒性其优化设计实验。

实验一：针对嵌入式网络电子信息系统利用改进算法和决策效率评估法（A算法）、信息检测与故障诊断方法（B算法），随机对其鲁棒性实现优化设计的实验，经过多次实验，并在不同次数的实验之后，对不同算法之下鲁棒性实现有效的对比。通过科学的对比，发现在对系统鲁棒性进行优化设计当中，使用改进算法要比使用其他两种算法更优，改进算法之所以比另外两算法更好，主要是由于其首先根据系统实际结构特点进行详尽的分析，并且把系统失效模式有效地分为多极限状态与单一极限状态两者不同情况来看待，并分别针对两种不同状态实现对系统失效概率的有效计算，并在获取失效概率基础上给出了系统的鲁棒性相应优化功能的函数，促使针对系统实现的鲁棒性相关设计更有保障[6]。

试验二：对系统进行鲁棒性改进与优化设计，分别利用A算法和B算法、改进算法进行三次实验，在不同次数试验中，三种算法在运行时间上存在一定的差异，结果见表1。

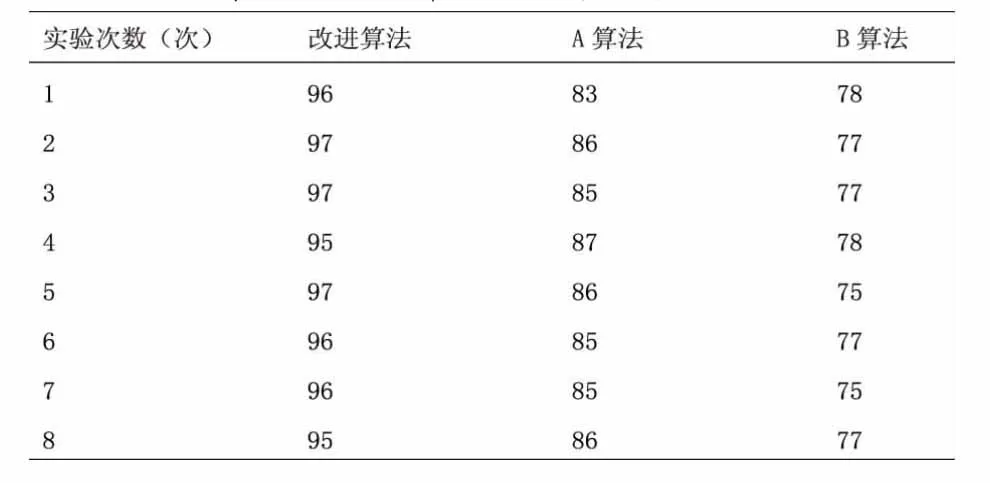
表1 不同算法运行时间对比（S）

通过表1发现，两种普通算法的时间效率都要比改进算法时间效率低。改进算法获得较高的时间效率，主要源于其将粒子群优化与混沌优化进行了深入融合，并通过科学的方法获取相应功能函数，使嵌入式网络电子信息系统可以在优化后的一定区域范围内完成动态搜索，并根据相应目标函数实现系统鲁棒性设计相应全局的最优解，促使系统相应鲁棒性的优化设计更加精确。

五、结束语

由于目前现用的算法在实现嵌入式网络电子信息系统相应鲁棒性优化过程中存在不足，因此本文提出在混沌粒子群算法改进的基础上对系统实现鲁棒性的优化设计，有效地结合了系统结构上的特点，分为两种状态进行有效计算，并科学地动态搜索之后，获得鲁棒性设计当中全局最优解的判定，并经过实验和仿真，得出该方法精确度非常高，具有良好适用价值。