一类BP神经网络优化评分预测的协同过滤推荐算法
王右雪,苏清华,胡中波
(长江大学信息与数学学院,湖北 荆州 434023)
更快更精准的推荐结果一直是国内外专家在推荐算法领域所追求的目标。当前被广泛关注的推荐算法之一是协同过滤推荐算法[1]。协同过滤推荐诞生于20世纪90年代,它在解决无特定目标的信息检索问题上有着显著的优越性[2]。常用的协同过滤算法依次经过数据表示、查找最近邻集合和项目评分推荐等3个阶段来完成推荐[3]。在数据表示阶段,根据用户对项目的评分数据构建用户对项目的评分矩阵,对于矩阵有降维[4]、填充[5]、变形为图的结构[6]等代表性方法;在查找最近邻阶段,以用户间相似性作为标准寻找到目标用户的相似近邻集合,寻找方法除皮尔逊相关系数法、余弦相似度[7]等原始方法外还有与智能算法、用户信息相结合的改进算法[8,9];在项目评分预测阶段,要做到先对用户的未评分进行评分,然后根据评分产生推荐结果。
由于评分预测方法直接关系到最后推荐结果的优劣,所以评分预测受到多位学者的重视。自1994年Resnick提出基于平均分的预测公式后,Resnick公式成为了推荐系统领域最常见的评分公式[10,11],但在其之后也有诸多学者对评分公式加以改进。Srisuwan P提出了一种基于贝叶斯的评分公式[12];罗亚引入了浏览时长的标签,以便做出更好的决策[13];雷鸣和朱明引入情感的惩罚度概念[14],以达到改善推荐效果的目的。
以上基于Resnick公式的改进方法均有效地提升了评分预测的效果,但若能在此阶段挖掘出用户更精准的个性化差异信息,或许能获得更精准的推荐结果。基于这一思路,笔者提出一类使用BP神经网络优化评分预测的协同过滤推荐算法(简记为BP-RF)。BP-RF算法的核心思想是:提出一种基于用户评分频数的BP神经网络优化评分预测模型,替换相应推荐算法中的Resnick模块。为了检验BP-RF算法类的性能,笔者应用上述思想改进了皮尔逊推荐(PFC)[7]、模糊混合用户推荐(FHUR)[8]和改进的Top-N推荐(ITop-N)[15]等3种代表性的算法。试验结果表明,BP-RF算法框架能够有效地降低各推荐算法计算结果的平均绝对误差MAE,对于稀疏数据,改进的算法仍然可以提升系统的推荐精准度。
1 协同过滤推荐算法
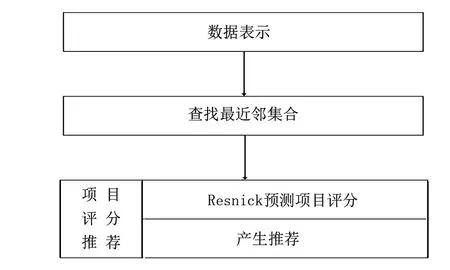
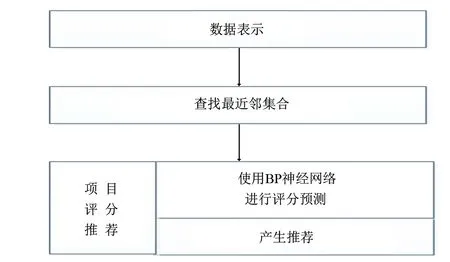
图1 推荐算法流程图
协同过滤推荐算法自1992年被提出来后一直是被广泛研究和应用的推荐方法之一[16]。协同过滤推荐算法主要通过对历史数据的分析,找到用户可能感兴趣的项目推荐给用户。可以分为图1所示的数据表示、查找最近邻集合和项目评分推荐3个阶段。
在数据表示阶段中,将用户对项目的原始评分用矩阵R:
(1)
来表示,其中Rij代表用户i对项目j的评分。
在查找最近邻阶段中,将2个用户的相似度作为衡量用户距离的标准。用户间相似度有着多种计算方法,常见的有以原始的余弦相似性[7]等方法为代表的距离值衡量用户相似度算法、以皮尔逊相关系数[7]等算法为代表的非绝对距离值衡量相似度算法、以模糊混合用户推荐[8]为代表的结合用户信息的推荐方法。计算目标用户与其他用户的相似度后,选择最相似的Top-N个用户标记为相似近邻集合NB-Su。
在寻找到相似近邻集合后,需要根据集合内各用户的评分预测目标用户的评分。在这一过程中最常使用的是Resnick评分公式[10],计算方法如下:
(2)
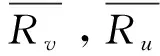
在预测到用户可能感兴趣的项目后,将其推荐给目标用户后完成推荐过程。
2 改进的BP-RF算法
改进的BP-RF算法依然保持常用协同过滤推荐算法的三阶段式框架,不同的是,应用一个基于BP神经网络的评分预测方法替换了推荐算法第3阶段中的Resnick模块。该改进旨在应用BP神经网络挖掘用户评分频数中的差异信息,进而提升算法推荐的精准度。
2.1 基于BP神经网络的评分预测方法
BP神经网络理论体系完善,在推荐系统中也有应用[17]。基于BP神经网络的评分预测方法首先将相似近邻集合中用户的评分整理成为各评分项目的评分频数,然后使用BP神经网络对数据进行学习训练,再使用训练完成的神经网络进行分数(评分)预测,最后根据预测结果产生Top-N推荐。
使用BP神经网络进行评分预测,需要统计相似近邻集中各用户对不同项目的各评分的总个数,记作Fi=(x1,x2,x3,x4,x5,x6),Fi为项目i的评分频数。在评分频数Fi中,xj分别代表用户近邻集中评分为j的用户个数。特别地,当j=6时,xj代表近邻集中未评分的用户个数。以下为评分频数转化示例。
表1数据是某一用户的8位相似近邻对3个项目的评分记录。以项目1为例,8位用户评1~5分的个数分别为0,2,1,0,0,并有5位用户未评分,所以项目1的评分频数F1=(0,2,1,0,0,5)。同理可得项目2,3的评分频数分别为:F2=(0,0,1,1,1,5);F3=(0,1,1,2,2,2)。

表1 用户评分矩阵示例
由于用户评分具有稀疏性,有极大可能出现未评分项目,这类数据对神经网络训练无意义,所以定义集合C1,C2,C3,C4确定可用数据与无用数据。如图2分类,定义如下:
C1:目标用户u评分,且近邻集合中至少有一人评分的项目集合
C2:目标用户u评分,但近邻集合中无人评分的项目集合
C3:目标用户u未评分,但近邻集合中至少有一人评分的项目集合
C4:目标用户u未评分,且近邻集合中无人评分的项目集合
在进行评分预测时,BP神经网络使用一层神经网络就可以得到很好的结果。所以,采用三层BP神经网络(输入层,隐含层,输出层)构建预测模型。训练样本为LF=[Fd]T,d∈C1,期望输出值是目标用户u的正确评分Ru=[Rd]T,d∈C1,网络训练完成,进行预测时输入值是IF=[Fd]T,d∈C2,期望输出值即为最终的预测结果FRu=[Rd]T,d∈C2。
BP神经网络的训练以表1数据为例,假设目标用户u对项目3未进行评分,则C1=[1,2],C2=[3]。此时训练样本LF=[F1,F2]T,期望输出值Ru=[2,4]T。BP神经网络整体数据传输如图3所示。
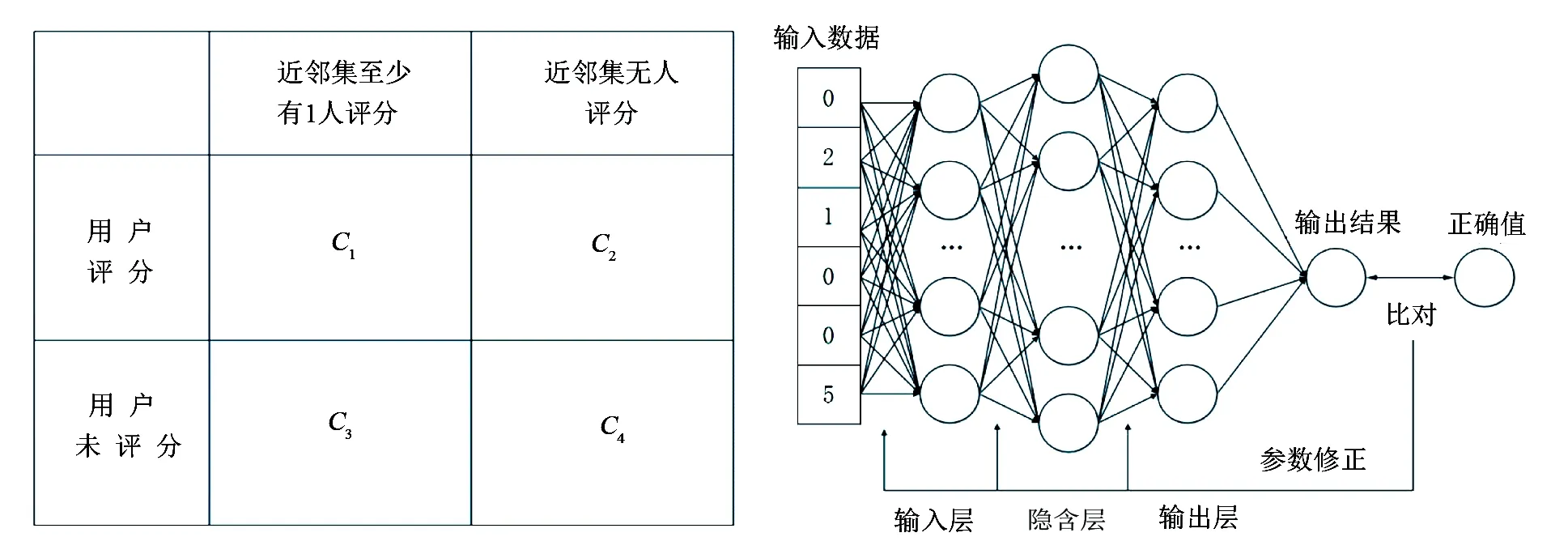
图2 数据划分示意图 图3 神经网络工作图
BP神经网络工作分2个部分:首先是训练样本正向传输,该过程中,输入信息激活各层的函数直到在输出层得出结果;然后是输出数据与期望输出值的误差ε计算,误差ε的反向传输可以调节各层权重与阈值,算法伪码如下:
训练过程
输入:训练样本LF,期望输出值Ru,
最大训练次数:Genmax,迭代次数gen,
学习速率learn
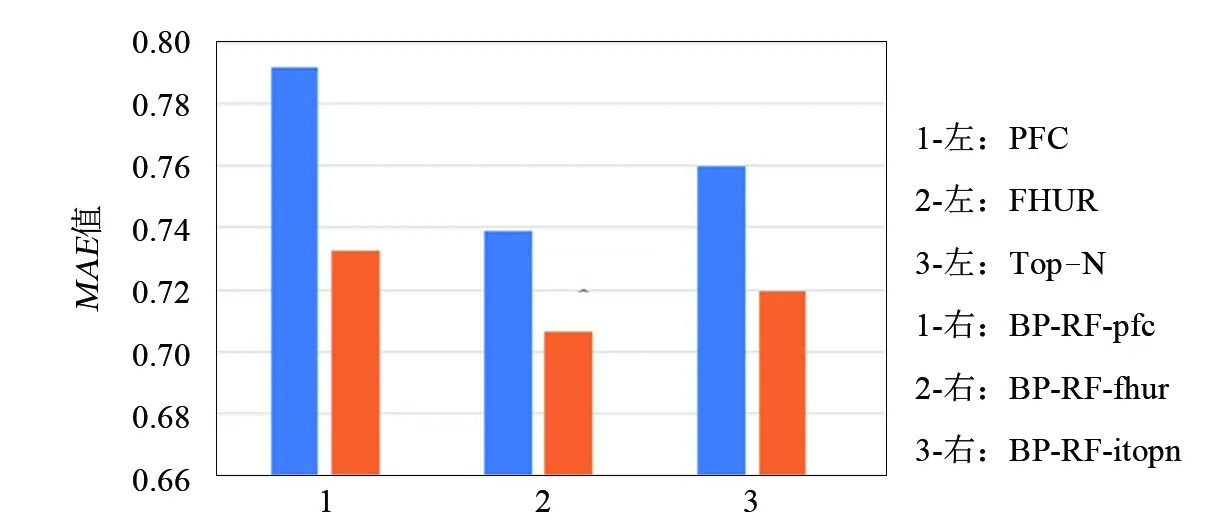
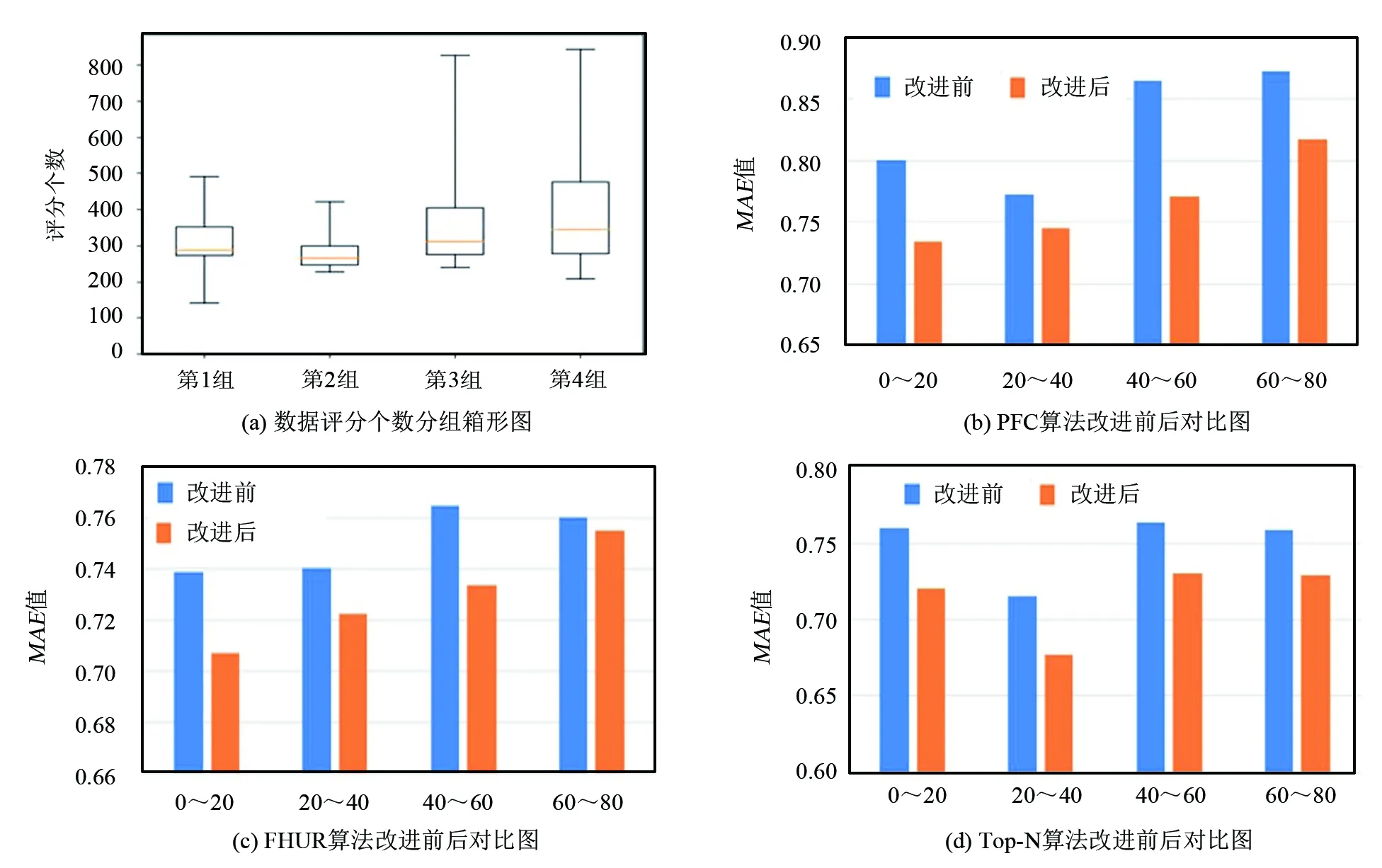
Whilegen Ifgen=1: 初始化神经网络参数ω,b Else: 修正ωi,b b=b+learn*ε 使用Sigmoid函数预测输出值 将R′与R的差值ε反馈回神经网络参数, ε=R′-R gen=gen+1 输出:训练完毕的ωi,b 预测过程: 输出:FRu 图4 改进后推荐算法 基于BP神经网络评分预测的推荐算法如图4所示: 改进后的协同过滤推荐算法(BP-RF)步骤如下: Step1:数据表示。根据用户浏览历史,构建矩阵R。 Step2:寻找相似用户集合。选择一个相似度衡量的标准,并根据标准选择最相似的N个用户构成目标用户的相似近邻集NB-Su。 Step3:BP神经网络项目评分预测。使用BP神经网络根据第2步中的相似近邻集NB-Su的评分频数预测目标用户未评分项的分数进行预测。预测完后根据评分结果推荐给用户会喜欢的项目,完成推荐。 设计了2组试验。第1组试验验证BP-RF算法框架对推荐算法的提升效果,试验选取PFC算法、FHUR算法和ITop-N算法作为被BP-RF算法框架提升的对象。其中,PFC算法是经典的推荐算法代表,FHUR算法是挖掘用户信息的推荐算法代表,ITop-N算法是经过聚类并考虑用户、项目双重相似性的算法代表。改进后的算法依次简记为BP-RF-pfc、BP-RF-fhur和BP-RF-itopn。 试验过程中的参数设置如下:输入层节点数:6;隐含层节点数:7;输出层节点数:1;迭代次数:1000;样本数据大小:card(C1);学习速率:0.9;容错率:0.01;激活函数:Sigmoid函数。 第2组试验是为了验证BP神经网络评分预测模块与算法结合进行推荐后,推荐效果与用户的评价个数之间的关系。测试集每20个用户一组画出其评分个数的箱型图,然后分析算法改进前后的MAE值与用户评分个数的关系。 选取推荐领域常用的Movie-lens-100K数据集作为试验数据集。该数据集内有多组训练数据与测试数据,选取任意一组训练数据作为试验训练集,对应测试数据前80个用户集合作为测试集,然后进行试验。 试验效果采用平均绝对误差MAE作为评价指标[18],验证算法改进的效果。MAE值是通过计算预测的项目评分和实际项目评分之间的偏差度来说明评分预测结果的准确性。MAE值越小,推荐效果越佳。当用户实际评分集合表示为{qi|i=1,2,…,n},预测的用户评分值表示为{pi|i=1,2,…,n}时,MAE计算公式为: (3) 图5 推荐结果对比 图5是第1组试验的结果图,由图5可以看出,笔者提出的BP神经网络优化评分预测方法的结果 (每组右侧数据)与3种算法未改进前的结果(每组左边数据)对比,改进后算法显著提高了推荐效果。对于相对成熟的模糊混合用户推荐系统和改进后的Top-N算法,MAE值分别降低了4.3%和5.2%,针对原始的皮尔逊推荐算法,改进后算法推荐效率大大提升,使MAE值降低了7.4%。 接下来是测试集的分组试验。将Movie-Lens-100K的测试数据集每20个用户划分为一组并进行箱形图绘制,然后将每组数据都进行3组算法对比试验,结果如图6所示。 图6 数据集分组分析及试验数据结果 从图6可知,第2组测试数据评分密度最均匀小;算法在第2组的推荐效果有所提升,第4组数据平均评分密度较大,但评分密度差异同样较大,所以推荐质量较第2组略差;在数据的密度不同的情况下,3组算法的MAE值表明:不论数据情况是稀疏或稠密,使用神经网络进行评分预测均可以改善原始算法的推荐效果。 针对协同过滤算法中Resnick评分模块及其相近改进模块的不足,提出了一类应用BP神经网络优化评分预测的协同过滤推荐算法,该类算法应用BP神经网络挖掘出用户评分频数间的差异信息来指导推荐。在Movie-Lens-100K数据集上的数值试验展现了该类算法的优越性。此外,BP-RF算法与其他算法融合度较高,可改进多种依靠评分公式产生推荐结果的推荐系统,使用范围广泛。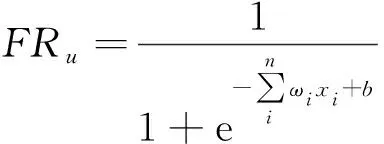
2.2 基于BP神经网络评分预测的推荐算法
3 试验
3.1 试验设计与参数设置
3.2 数据集与评价指标
3.3 试验结果及其分析
4 结语

