基于极值理论的互联网金融操作风险测算

陈耀辉，姜婷

(南京财经大学经济学院，江苏 南京 210023)

近年来，随着互联网技术的发展和“互联网+”时代的到来，传统的金融业发生转变，互联网金融应运而生。“互联网金融”是一种互联网技术与金融业务全面交互、关联、延展和创新而产生的新型金融，是对传统金融模式的一种延展和创新。互联网金融产业的产生给人们的社会经济生活带来了巨大改变，第三方支付、P2P 网络借贷、众筹融资等互联网金融业态为人们的日常消费提供了极大的便捷，也为人们筹借、投资资金提供了一种新型的渠道。但在互联网金融快速发展的同时，各种问题也层出不穷，平台体系的技术漏洞、员工专业素养的参差不齐、内部欺诈的存在、金融市场审查与监管不足等操作风险都会对互联网金融的发展产生极大的危害。

以互联网金融机构中第三方支付平台为例，支付宝作为第三方支付平台的代表多次被曝安全漏洞。2017年1月，支付宝被曝安全问题，熟人只要知道最近买过的东西，且2人有共同好友，就能较为轻易地通过验证，登录他人支付宝账户；2018年3月15日，央视的315晚会也指出了支付宝平台人脸识别支付的严重漏洞，不法分子利用软件修改人脸图片便可直接进行脸部识别，轻易盗刷用户账号。此外，2014年曝光广东某旅游休闲服务“加油金”业务涉嫌非法吸收公众存款造成资金风险敞口约6亿元，上海某企业管理服务有限公司挪用客户备用金造成资金敞口约7.8亿元等等，互联网金融机构一系列操作风险事件频频发生。

风险事件的发生预示了互联网金融机构在运营过程中存在着巨大的安全风险隐患，也说明了我国对于互联网金融行业的监管方面存在不足。目前，我国的互联网金融市场发展潜力巨大，但仍处在发展初期，面临很多风险在所难免，尤其是与技术平台相关的操作风险。用现代金融风险测量技术度量互联网金融的操作风险，建立一套合理的互联网金融操作风险识别、度量、监控和控制体系，是促进互联网金融市场健康良性发展，有效防范金融形式创新造成的新型操作风险的必然要求。为此，笔者对互联网金融的操作风险损失的分布进行了研究，并对互联网金融领域的操作风险进行测度。

1 文献综述

1.1 关于操作风险的研究综述

国外对于操作风险最权威的定义是在巴塞尔委员会制定的《巴塞尔协议》中，1988年7月，巴塞尔委员会在瑞士的巴塞尔通过“关于统一国际银行的资本计算和资本标准的协议”，即《巴塞尔协议》。此后通过1999年和2010年的2次修订，形成了一套比较成熟的风险理论体系。巴塞尔新资本协议中定义“操作风险是指由不完善或有问题的内部程序、人员、系统或外部事件所造成的损失”。目前，业界研究操作风险普遍使用这一操作风险定义[1]。在此基础上，众多的国外学者对操作风险进行定量研究。1997年，Embrechts等最早采用EVT理论对操作风险进行度量[2]，随后，Embrechts又在2006年采用多维极值理论度量了操作风险，他认为极值理论能够较好的度量操作风险[3]。2004年，Moscadelli利用EVT理论分析了巴塞尔银行监管委员会定量影响测算统计的47000个操作风险损失数据，认为广义Pareto分布(GPD)能够很好的拟合操作风险的上尾[4]。2006年，Patrick采用公开的极值数据和极值理论度量了操作风险，并认为银行操作风险资本金大于市场风险资本金[5]。

国内对于操作风险的研究较晚。2005年12年31日，中国银监会下发《商业银行风险监管核心指标(试行)》，首次将操作风险指标同信用风险指标、市场风险指标并列作为中国商业银行风险监管核心指标，并将操作风险的定义基于中国商业银行发展的特点进行调整。“中国商业银行的操作风险为由于商业银行公司治理的不到位、内部程序和业务流程的不完善、人员的失误或舞弊、系统的失灵或缺陷以及外部事件”。2007年，高丽君针对我国商业银行操作年度损失数据缺乏亦不满足常用分布的情况，根据Bootstrapping模拟的特点和优点生成操作风险年度损失数据，利用极值算法估计操作风险损失分布并预测操作风险极端损失，得出操作风险经济资本[6]。同年，刘睿，詹原瑞和刘家鹏在损失分布法的框架下，以中国商业银行的内部欺诈损失数据为样本，借助POT模型对内部欺诈风险强度和频率进行估计，并使用基于吉布斯抽样的贝叶斯MCMC方法估计POT模型的参数，通过极值理论对中国商业银行的内部欺诈风险进行度量，并估计了相应的经济资本[7]。2008年，陈倩和李金林以我国的517个风险损失数据为基础，将四参数的g-h分布用于操作风险损失强度拟合中，实证结果显示，g-h分布能较好的捕获操作风险损失分布的“厚尾”特性，对操作风险损失分布的拟合效果最好[8]。2017年，莫建明、吕刚和高翔等认为重尾分布非预期损失估计值具有不确定性，并以操作风险度量为例，在Pareto分布下研究损失分布法度量误差变动规律，他们发现，随着监管资本变动，度量误差变动具有非常高的敏感性，损失分布法度量误差具有不可预测性，损失分布法存在着重大缺陷[9]。

1.2 关于互联网金融风险的研究综述

国外学者首先对互联网金融问题进行了研究。2007年，Thomas Meyer对互联网金融其中的一种模式——P2P进行了描述，指出了P2P信贷中所存在的风险，对比了低风险和高风险借贷人进行P2P时的不同[10]。2009年，Ming-Chi Lee对网上银行进行研究，运用技术接受模型和集成计划行为理论模型对感知风险理论的5个方面——金融风险、安全与隐患、性能、社会和时间风险进行研究分析，结果表明，使用网上银行的不利影响主要有安全隐私风险、金融风险等，积极影响在于感知利益、态度和感知有用性[11]。2011年，EC Chaffee和GC Rapp在Dodd-Frank法案出台后研究了P2P网络信贷的监管问题，在文中他们从联邦和州2个层面分析P2P网络借贷问题和监管问题，讨论P2P起源和其特殊风险性，提出针对P2P网络借贷风险的多部门监管方法[12]。2012年，JER Lee等对网络购物时的在线支付问题进行了研究，通过安全问题和信用卡安全码2个实验分析了在网络购物支付过程中的风险[13]。

国内对于互联网金融风险的研究起步较晚，相应的研究成果也较少。自2012年和2013年之后，对于互联网金融的相关研究飞速地增加。2012年，谢平和邹传伟等首次提出互联网金融的概念，研究了互联网金融的模式，并分析了互联网金融的支付方式、信息处理、资源配置等问题[14]。2013年，闫真宇提出互联网金融业务活动产生的不确定和不可控是造成互联网金融风险的主因，互联网金融风险主要由法律规范、技术风险、业务管理、货币政策、洗钱犯罪5大类因素导致[15]。同年，张松、史经伟、雷鼎等对互联网金融形势下的操作风险新问题进行研究，他们认为，在互联网金融形势下，操作风险主要包括金融业信息化的操作风险、行业间的关联性风险和消费者操作不当风险[16]。

基于以上文献综述，国内外专家学者对于操作风险的研究大多集中于商业银行领域，对于互联网金融的研究多集中在整体领域和定性领域，对于互联网金融操作风险的专项研究及定量研究较少。

2 操作风险与极值理论

根据巴塞尔新资本协议中对操作风险的定义，“操作风险是指由不完善或有问题的内部程序、人员、系统或外部事件所造成的损失”。引发操作风险的诱因或事件具体可分为7类：内部欺诈，外部欺诈，雇佣及工作安全，顾客、产品与商业行为，有形资产损失，涉及执行、交割及交易过程管理的失误。结合操作风险的诱因，我国互联网金融行业所面临的操作风险主要可以概括为以下几种形式：违规经营风险，即违反现行的相关法律规定开展经营活动，主要包含违约挪用客户资金，欺瞒客户资金流向，超规模违规发行网络支付产品等；操作失误风险，即由于内部工作人员的操作失误而造成的风险；网络安全风险，即因为网络安全漏洞或支付平台漏洞而造成的风险；外部关联风险，即由于外部关联商失误而造成的风险，互联网金融行业大多公司依托外界服务商或服务外包，服务商服务水平参差不齐、系统保障投入不足等问题也会造成操作风险。

目前，互联网金融机构及相关监管部门已经对操作风险的管理的重要性有了一定的认识，相关专家学者也对引发操作风险的各种诱因进行分析，然而由于操作风险自身的特点，操作风险的量化管理依然是风险监管的一个难点问题。在传统的商业银行领域，依据商业银行操作风险的特点，相关监管机构及各专家学者已经提出了一系列的操作风险计量模型：《巴塞尔新资本协议》提出利用标准法、损失分布法、记分卡法等计量操作风险，专家学者在此基础上大多利用历史模拟法、蒙特卡洛模拟以及极值理论模型对操作风险的VaR值进行测度。由于互联网金融中所面临的操作风险操作损失数据多服从“尖峰厚尾”的特征，损失的尾部性比较严重，基于此，笔者利用极值理论对互联网金融操作风险进行度量。

极值理论是处理与概率分布的中值相离极大的情况的理论，常用来分析概率罕见、模型中存在y=z-μ极端值的情况，极值理论包括2类模型：BMM模型和POT模型。BMM模型是通过对数据进行分组，然后在每个小组中选取最大的一个构成新的极值数据组，并以该数据组进行建模，BMM模型适用于具备季节性的数据。POT模型则是通过设定一个阈值，把所有观测到的超过这一阈值的数据构成新的数据组，以新数据组作为建模的对象，POT模型对数据要求的数量比较少，是现在经常使用的一类极值模型。因为操作风险损失数据不具备明显的季节性特点，且商业银行操作风险分析中多采用POT方法，笔者在研究互联网金融领域的操作风险中也采用POT方法。

POT模型是研究极端数据的一种方法，POT模型通过设定阈值，把所有观测到的超过这一阈值的数据构成新的数据组作为建模的对象。假设F(x)为变量x的累计分布函数，μ为x右端尾部的阈值，任取y>0，x介于μ和μ+y之间的条件概率为：

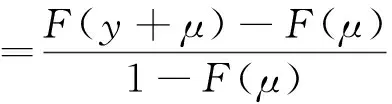
(1)

式中，y=z-μ表示超量损失。

根据Gnedenko的研究，对于多种概率分布F(x)，随着μ的增加，分布Fμ(y)趋向于广义Pareto分布，累计分布函数为：

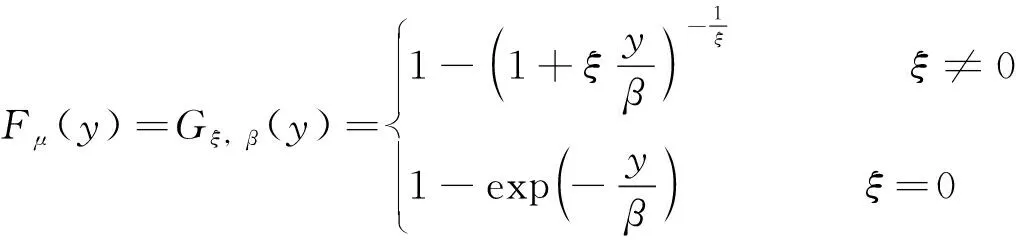
(2)

式中，ξ与分布的形状有关，决定了尾部分布的厚度；β是分布的尺度因子。参数ξ,β通过最大似然方法进行估计。

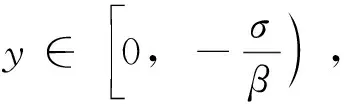
3 互联网金融操作风险实证分析

互联网金融起步较晚，发展较快。互联网金融操作风险问题虽然是急需解决的问题，但是目前所能搜集到的数据较少，对分析的准确性可能会产生影响。笔者基于搜集到的数据对互联网金融操作风险损失数据服从的分布进行确定，再利用蒙特卡洛模拟方法按照该分布对数据进行模拟扩充，以提高分析结果的准确性。

3.1 数据统计

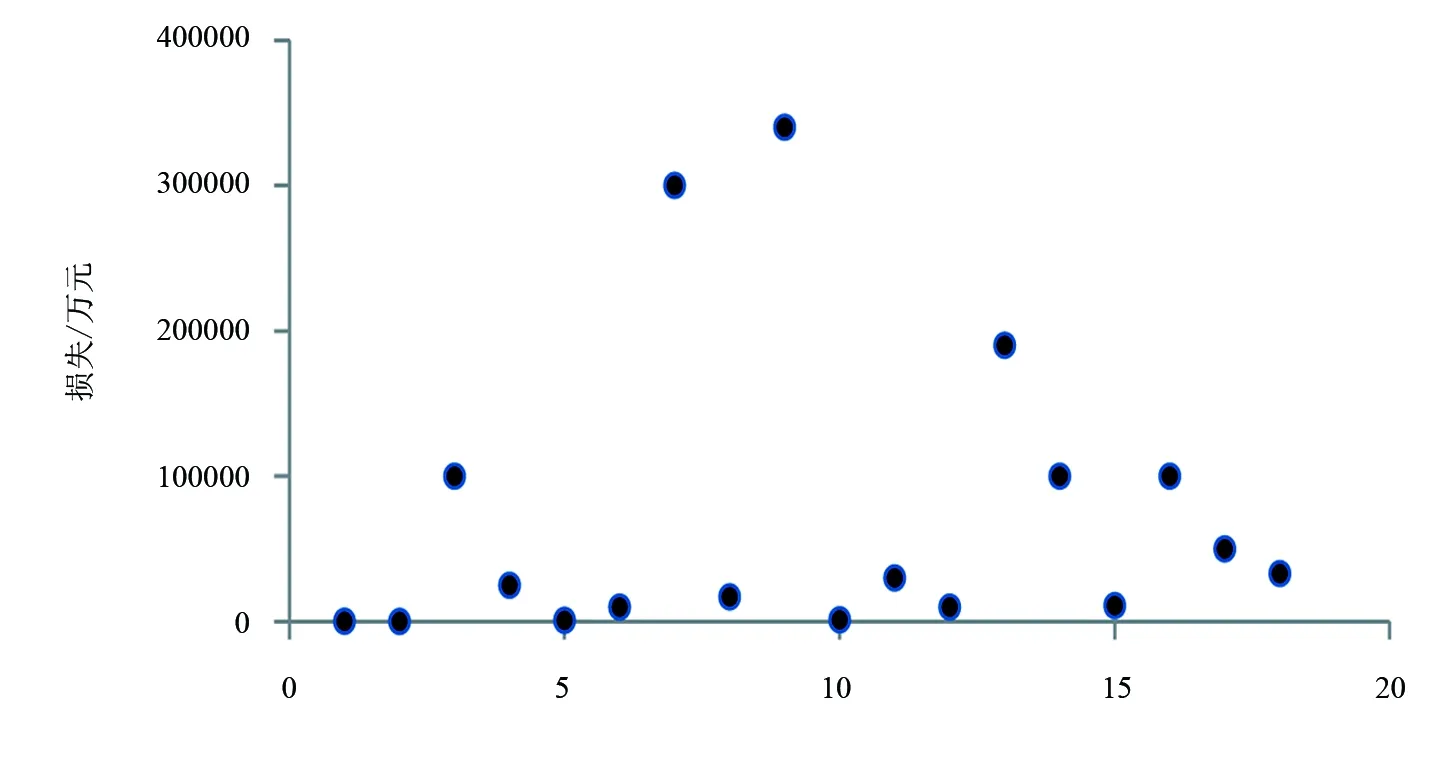
图1 互联网金融操作风险损失分布散点图

通过对wind数据库资讯和resset金融数据库中的每日资讯进行整理，统计了2012年以来互联网金融领域操作风险事件的信息，共统计事件25件，其中包含违规经营风险事件12件，网络安全风险事件8件，操作失误风险事件3件，外部关联风险事件2件，其中，18件事件的损失可知，分布的散点图如图1所示。

由图1可知，操作风险的损失分布数值较大，操作风险的损失大部分集中于20亿元以下，但也有极少部分超出30亿元。

样本数据的统计特征如表1所示。由表1可知，操作风险损失样本数据的JB(Jarque-Bera统计量)值为9.5383，P值为0.0085，损失样本不服从正态分布。从统计的偏度和峰度来看，偏度大于0，说明分布是右偏，即有一条长尾拖在右端，数据右端有较多的极端值，峰度大于3，说明统计的操作风险数据分布与正态分布相比相对陡峭，为尖峰。

表1 互联网金融操作风险损失样本数据的统计特征

3.2 数据的厚尾性及分布的检验

根据商业银行操作风险的一般分布，笔者假设互联网金融操作风险服从极值理论，损失数据服从广义Pareto分布。下面将对互联网金融操作风险损失数据是否服从广义的Pareto分布进行检验。

样本数据的Hill图如图2所示，当阈值选择在10000万元～20000万元时，形状参数ζ的数值趋于平稳，为保障结果的的准确性，分别选择阈值μ1=10000万元，μ2=15000万元，μ3=20000万元进行分析。

利用搜集到的互联网金融操作风险损失数据和最大似然方法估计得到阈值μ1=10000万元，μ2=15000万元，μ3=20000万元时参数ξ，β的数值，如表2所示。

图2 样本数据Hill图

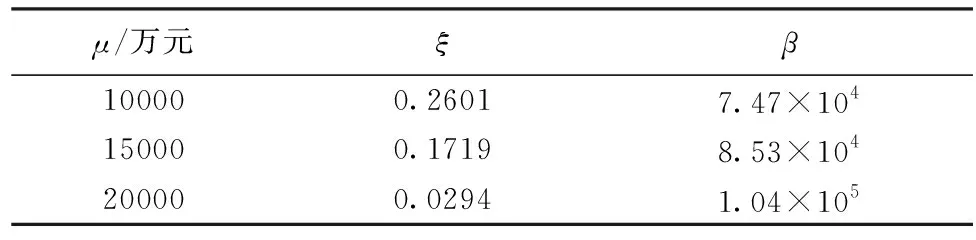
μ/万元ξβ100000.26017.47×104150000.17198.53×104200000.02941.04×105

由表2可知，当阈值μ1=10000万元时，参数ξ1=0.2601，当阈值μ2=15000万元，参数ξ2=0.1719，当阈值μ3=20000万元时，参数ξ3=0.0294。在不同阈值下，参数ξ的估计值都大于0，这说明基于已统计的互联网金融操作风险的相关数据，互联网金融操作风险服从广义的Pareto分布，互联网金融操作风险的损失数据存在着厚尾的特征。

3.3 数据的模拟

由上可知，互联网金融操作风险损失数据服从广义的Pareto分布，通过蒙特卡洛模拟方法模拟数据来对互联网金融操作风险的原损失数据进行扩充，模拟的次数越多结果越准确，但所用时间也越长。为了保证一定的精确度，笔者选择的模拟次数为10000次。对模拟出的数据进行描述性统计，得到模拟损失数据的统计特征如表3所示。

表3 互联网金融操作风险模拟损失数据的统计特征

由表3可知，模拟损失数据的平均值为73374.43，偏度为1.7617，峰度为4.4599，与表1的原数据比较相差不大，拟合的效果较好。对模拟数据进行Hill估计，得到图3所示的Hill图。

由图3可知，在模拟数据中，当阈值选择在25000万元时，形状参数ζ的数值趋于平稳，利用最大似然进行估计，可得知，当阈值为25000万元时，参数ξ、β的数值分别为0.012、72141。

3.4 操作风险在险价值

当Fμ(y)的分布足够接近广义Pareto分布，且ξ≠0时，在α的置信水平下，风险的在险价值为：

(3)

式中，E(y)，σ分别为超量损失y的均值和标准差。

由式(3)可得在90%、95%、99%、99.97%置信水平下的互联网金融操作风险的VaR值，如表4所示。

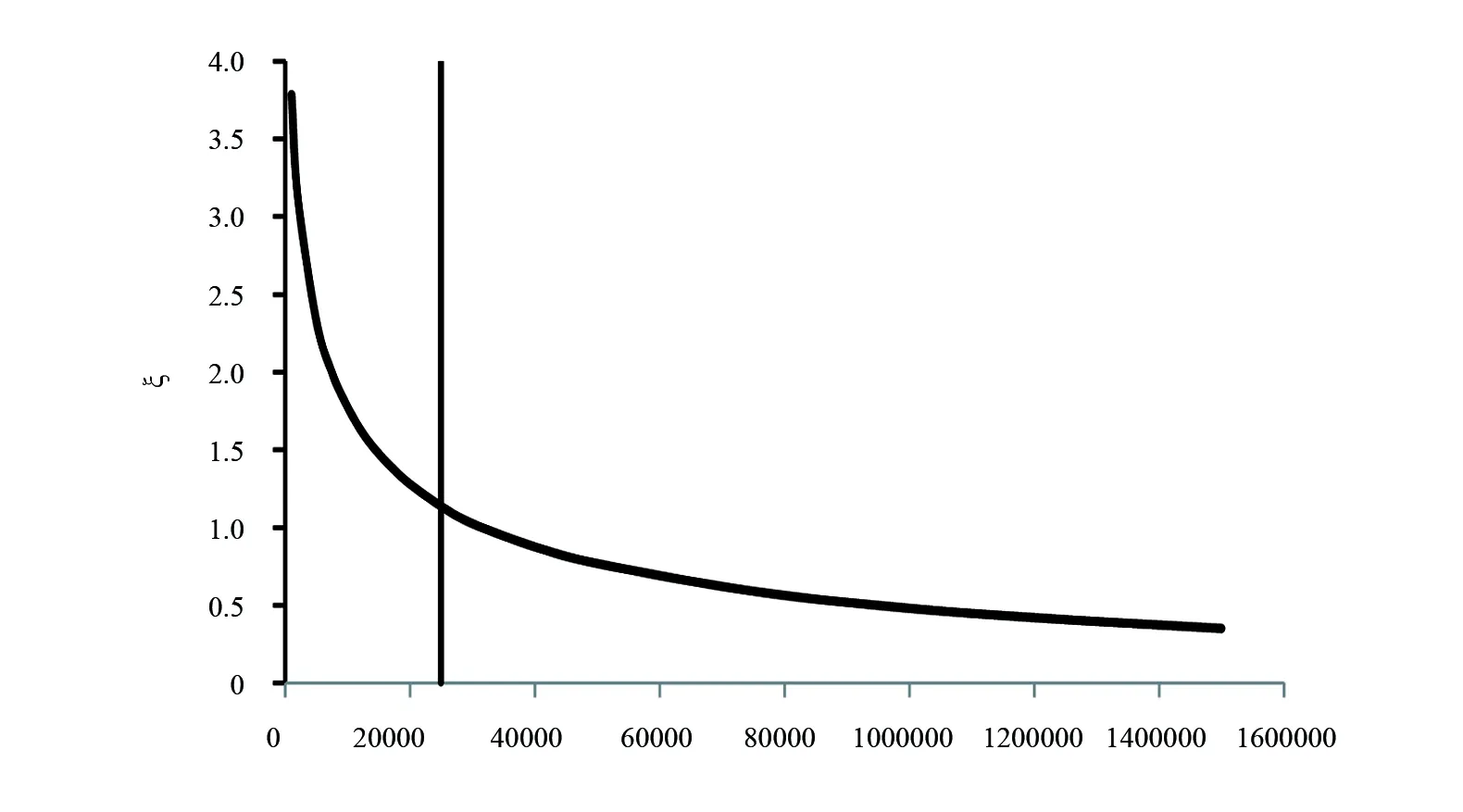
图3 模拟数据Hill图

表4 不同置信水平下的互联网金融操作风险VaR值

由表4可知，互联网金融机构需要配置的操作风险资本金随着置信水平的增大而变多，在模拟10000次的情况下，90%的置信水平下，互联网金融机构为操作风险应配置296175.8万元的资本金，如果参照传统商业银行新资本协议中对操作风险99.9%的置信水平标准，互联网金融机构为操作风险配置的资本金应该更多，为657343.3万元。这表明互联网金融机构需要配置足够的操作风险资本金以有效的预防风险。

4 结论与建议

对互联网金融领域的操作风险损失数据的分布进行估计，并用蒙特卡洛模拟方法对损失数据进行模拟扩充，引入传统商业银行中操作风险度量常用的极值理论方法对互联网金融领域中存在的操作风险进行测度。研究表明，互联网金融领域的操作风险损失数据服从广义Pareto方法，在90%的置信水平下，互联网金融机构为操作风险应配置296175.8万元的资本金，如果依据商业银行新资本协议99.9%的置信水平标准，互联网金融机构为操作风险配置的资本金为657343.3万元。这为互联网金融机构配置资本金提出了建议。

从近年来互联网金融操作风险事件种类发生频率来看，违规经营风险事件和网络安全风险所占比重最大，分别为48%，32%。这一方面要求互联网金融机构提高对员工专业素质和专业能力的培训，建立严格的监控机制和信息披露机制，加强对客户资金流向的监管；另一方面也要求互联网机构重视网络安全防护工作，构建好网络防护墙，不断开发和应用更安全、更稳定的网络工作及交易环境，以保护客户的信息与资金安全。

由于互联网金融行业刚刚起步，而操作风险本身属于比较极端的风险，所以笔者搜集的数据不足，研究可能存在一些误差；另一方面，笔者将互联网金融领域各业务平台看作一个整体来测算操作风险，但目前互联网金融涉及的范围很广，各平台中涉及到的操作风险的发生频率及损失程度也存在着差异，笔者未对这种差异性进行研究。此外，互联网金融领域存在一些小型的平台，比如P2P、众筹等，自身注册资金比较少，往往很难有充足的资本金预留给操作风险，对此，相关监管部门应设定互联网金融平台进入门槛，并根据互联网金融的特点创新操作风险的监管方式。