基于流形学习的约束Laplacian分值多标签特征选择

蒋伟东，黄 睿

上海大学 通信与信息工程学院，上海 200444

1 引言

多标签分类针对具有多个类别标签的实例进行类别划分，是数据挖掘领域的研究热点之一，已在文本分类、信息检索、生物信息提取等方面获得广泛应用[1-3]。与单标签分类一样，多标签分类也会因标记样本有限而受到维数灾难问题的影响，导致分类器性能降低。通过多标签特征选择技术降低数据维数，可有效提高分类器性能。

相对于传统单标签特征选择，多标签数据的特征选择更加复杂。张振海等提出基于信息熵的多标签特征选择算法，通过计算每个特征与标签间的信息增益关系以及设置信息增益阈值，剔除不相关特征，得到最佳特征子集[4]。文献[5]则是在原始的信息增益多标签算法基础上引入标签间的相关性以实现特征重要度排序。文献[6]提出一种融合特征排序的多标记特征选择算法，首先在标签下自适应粒化样本，构造特征与标签间邻域关系并进行排序，最后通过聚类融合形成新的特征排序。对已有单标签特征选择算法进行改造应用于多标签数据也是一种可行的方法。如：文献[7]通过对多标签数据相关性与特征权值的分析，提出基于ReliefF的多标签特征选择（Multi-Label ReliefF，ML-ReliefF）；Spolaor等提出基于Label Powerset处理方式的信息增益算法（Information Gain-Label Powerset，IG-LP），通过考虑不同的标签组合，将多标签直接转换为单标签，之后采用信息增益算法衡量每个特征与标签间的相关度[8]。Chang等提出一种凸半监督多标签特征选择算法（Convex Semisupervised multi-label Feature Selection，CSFS），通过最小化最小二乘损失函数进行稀疏特征选择，可用于大规模数据集[9]。Ma等提出基于多标签学习的稀疏特征选择算法（Sub-Feature Uncovering with Sparsity，SFUS），一方面通过稀疏空间选择出最具有辨别力的特征，同时也考虑不同标签间的相关性[10]。Alalga等将不同样本的类别标签相似性定义为软约束，并用以修正邻接矩阵，提出一种半监督的软约束Laplacian Score（Soft-Constrained Laplacian Score，S-CLS）[11]。

在多标签数据分类中，样本的类别标签通常为逻辑型，即若样本属于该类别则置为“1”，否则置为“0”。这样的表示方法没有考虑到不同类别标签对于同一样本的重要性往往是不同的。Hou等利用流形学习思想对类别标签的重要性进行量化，将逻辑型类别标签映射为数值型类别标签[12]。受此启发，本文提出一种基于流形学习的约束Laplacian分值多标签特征选择方法（Manifold-based Constraint Laplacian Score，M-CLS）。方法首先从数据空间对特征进行评分，利用逻辑型类别标签间的相似性修正Laplacian分值；接着在标签空间通过流形学习将逻辑型类别标签映射为数值型类别标签，并计算相应的Laplacian分值；两种分值之积为最终的特征分值。实验结果表明，所提M-CLS方法能提取出更有效的特征子集，获得更好的多标签分类性能。

2 本文算法

对于单标签数据，样本间的关系可以直接划分为同类和异类。但对于多标签数据，由于每个样本都具有多个类别标签，需要衡量不同样本间类别标签的相似性。定义样本xi与xj的逻辑型类别标签的相似性为：

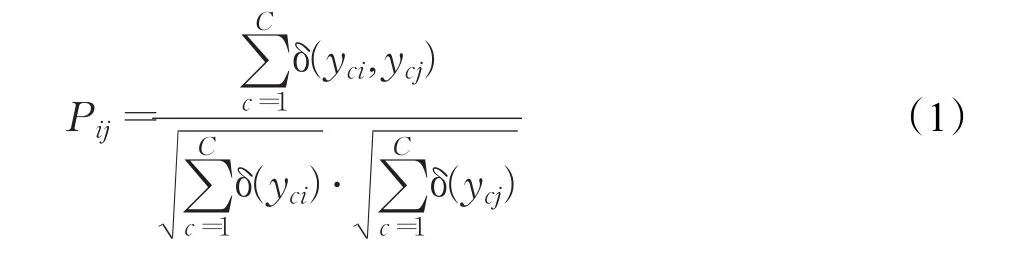
其中，δ(⋅)为狄拉克函数，有：

在此基础上定义特征空间邻接矩阵如下：

其中，t为可调参数。对于第n个特征 fn(1≤n≤N)，特征空间的约束Laplacian分值定义为[13]：

在多标签数据分类中，逻辑型的类别标签无法反映出实例所具有的不同标签的重要度。利用流形学习思想，将逻辑型标签转化为数值型，通过标签的实值体现不同类别标签的相对重要性[12]。根据平滑假设（即相邻的点很可能属于同一类别）[14]，特征空间的拓扑结构可以传递到类别标签的数值空间。通过极小化下式得到特征流形结构：

若 xj不是xi的近邻，则将置为0。通过求解最小二乘问题获得ψ。定义与逻辑型标签对应的实值标签为zi∈RC。在获得数据特征空间的流形结构后，类别标签的流形结构表示为：

在给定ψ的前提下极小化上式，获得实值标签z。实值标签一方面反映了同一实例具有的不同类别标签的重要度差异，另一方面也体现了同一类别标签对不同实例的重要度差异。

在此基础上，定义标签空间的邻接矩阵如下：

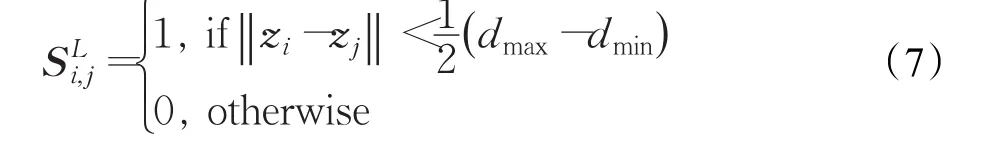
其中，dmax和dmin分别为实值标签间的最大和最小欧式距离。对于第n个特征 fn(1≤n≤N)，实值标签空间的Laplacian分值定义为：

结合式（4）和（8），对于第 n个特征 fn(1≤n≤N)，基于流形的约束Laplacian分值定义如下：

下面对M-CLS的流程进行了总结：

输入：数据集X，多标签集Y，近邻数k

输出：每个特征的M-CLS分值

1.根据式（1）、（2）、（3）计算特征空间的约束邻接矩阵SF，并以此计算DF和LF。

2.根据式（7）计算数值型标签空间的邻接矩阵SL，并以此计算DL和LL。

ford=1∶D

3.根据式（4）、（8）、（9）计算每个特征的M-CLS分值。

end

4.对特征按M-CLS值排序。

3 实验

为验证所提算法M-CLS的性能，在多标签数据集Recreation和Yeast上进行了特征选择与分类实验，并与4种多标签特征选择算法IG-LP、CSFS、SFUS和ML-ReliefF的实验结果进行比较。分类器为ML-KNN[15]，近邻数k设为10。采用汉明损失（Hamming Loss），排序损失（Ranking Loss），1-错误率（One Error），覆盖长度（Coverage）和预测精度（Precision）这5个性能评价指标进行性能评价[16]，其中，前4个指标与预测精度相反，值越小表示分类效果越好。表1给出了所用数据集的具体描述。

表1 实验所用数据集

表2、3分别列出了不同特征选择方法在数据集Recreation和Yeast上的分类结果。此外，还给出了采用全部特征时的分类性能指标，作为比较基准。可以看到，所提算法的5个指标与其他特征选择方法相比不但具有明显优势；而且也优于采用特征全集时的性能指标。图1进一步给出了不同方法对于Recreation数据选择不同特征数时的性能指标，横坐标为所选特征数，纵坐标为参数值，可以看到，特征选择方法的性能并没有随着特征数的增多而逐渐提升，而是存在明显起伏，这在M-CLS上表现的尤为突出。M-CLS在选择较少特征数时体现出更好的性能，说明此方法在特征子集规模相同情况下能选择出更有效的特征构成子集。

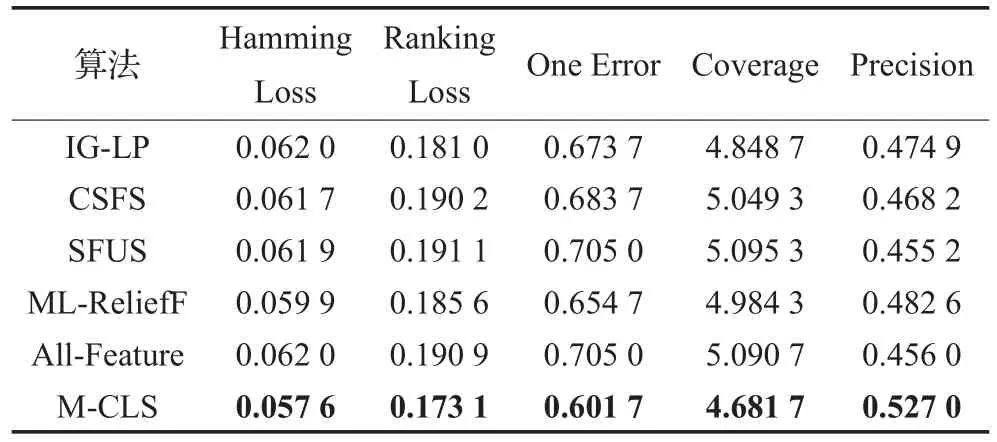
表2 不同方法在Recreation数据集上的性能比较

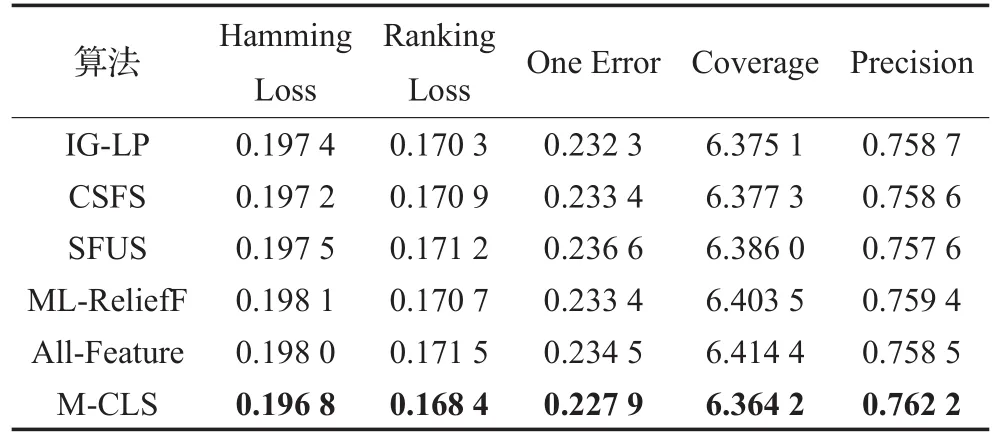
表3 不同方法在Yeast数据集上的性能比较

图1 Recreation数据集分类结果对比

表4、5列出了两个数据集采用不同方法进行特征评分时，所选出的最重要特征。可以看到，不同特征选择方法选择出的最重要特征均不同。本文所提算法MCLS在Recreation、Yeast数据集上选择出的最重要特征编号分别为Att493、Att34。

表4 不同方法在Recreation数据集上所选特征比较

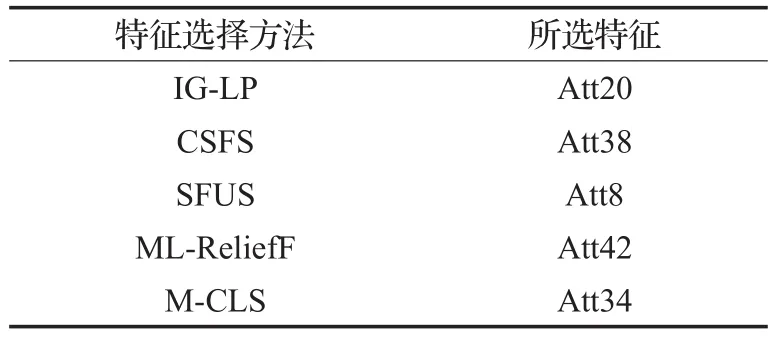
表5 不同方法在Yeast数据集上所选特征比较

4 结论

提出一种基于流形学习的约束Laplacian分值多标签特征选择方法M-CLS。本文方法首先在特征空间利用逻辑型类别标签的相似性对邻接矩阵进行改进，定义了约束Laplacian分值；接着基于流形学习将逻辑型类别标签映射为数值型类别标签，在实值标签空间定义新的邻接矩阵，由此定义Laplacian分值；最后将两种分值相乘获得最终的特征评分。实验结果表明，本文算法M-CLS能选择出更有效的特征构成子集，性能优于多种多标签特征选择方法。