基于改进蚁群算法的机器人路径规划问题研究

朱 艳，游晓明，刘 升，袁汪凰

1.上海工程技术大学 电子电气工程学院，上海 201620

2.上海工程技术大学 管理学院，上海 201620

1 引言

机器人路径规划问题是机器人学的一个重要研究领域，它要求机器人依据一定的优化原则（如能量消耗最小，行走路线最短，行走时间最快等等），在其运动空间中找到一条从运动起点到目标点的最优或者接近最优的路径，且此路径能安全躲避障碍[1-2]。为了解决路径规划问题已经出现大量的算法，如人工势场法[3]、Dijkstra算法[3-5]、A*算法[6]等。近年来学者从自然界的一些现象中得到启发，提出将遗传算法[7-8]、粒子群算法[8]、蚁群算法等智能仿生算法应用于机器人路径规划的研究。

在20世纪90年代，意大利学者Dorigo、Maniezzo和Colorni等人从生物进化的机理中受到启发，通过模拟自然界蚂蚁寻食的行为，提出了蚁群优化算法。尽管蚁群算法已经可以较为成功地解决路径规划的问题，但是算法容易陷入局部最优，无法得到全局最优路径，因此许多研究人员对其进行深入分析，提出改进的蚁群算法[9-10]，并且得到了广泛的应用。文献[11]针对基本蚁群算法容易陷于局部最优解这一问题，提出使用双种群蚁群同时进行搜索，在迭代过程中，若判断出算法陷入可能局部最优，则交换两个种群对应路径上的信息素，并同时双向动态自适应调整信息素挥发系数，虽然改进的算法在一定程度上提高了搜索的全局性，但仍然存在收敛结果不稳定的问题。文献[12]通过改进启发函数ηij，避免单纯使用导致蚂蚁贪婪当前最短路径，不仅提高了算法跳出局部最优的能力，也加快了算法的收敛速度，但改进算法在路径寻优方面还有待改善。文献[13]通过设定信息素初始值，改变信息素更新规则，引入最大最小信息素系统，对ACS算法易陷入局部最优这一缺陷进行改进，解的质量明显提高，但仍存在寻优过程中搜索时间较长的问题。以上改进虽然都对算法易陷入局部最优的问题有所改善，但仍存在算法搜索效率不高的问题，致使搜索时间较长。

针对蚁群算法搜索效率不高以及易陷入局部最优的问题，本文在ACS算法的基础上改进了其启发函数。为避免蚂蚁贪图局部最优偏离行进方向，在路径的后程引入了目标点的方向信息，启发蚂蚁以较大概率向目标点移动，提高算法搜索效率，同时在蚂蚁移动过程中动态调整权重系数，以改变目标点的方向信息对蚂蚁行动影响的大小。仿真结果表明，本文改进算法是有效且可行的，通过改进确实减少了算法的搜索时间，同时也在一定程度上提高了解的质量。

2 相关工作

2.1 A*算法

A*算法采用的是遍历搜索，它的核心在于利用启发函数估计路径中当前节点到目标点的代价，再从中选择付出代价最小的下一节点，通过这一过程减少路径搜索范围，搜索效率明显提高。这样将搜索区域进行简化的方法，改善了搜索环境，降低了问题的复杂度。

其中，g(n)表示起点到当前节点n的实际代价，h(n)表示当前节点n到目标点的估计代价，f(n)表示当前节点n的估价函数，即起点经过当前节点n到达目标点的最优路径的代价。

2.2 ACS算法

蚂蚁系统（Ant System，AS）是第一个蚁群优化算法（ACO），它是意大利学者Dorigo在1991年最先提出，并成功地用于求解著名的组合爆炸问题TSP问题，即旅行商问题。1996年，Gambardella与Dorigo等学者在Ant-Q算法的基础上进行改进，提出蚁群系统（Ant Colony System，ACS）[13-14]。

在ACS算法中，蚂蚁选择下一个节点时采用了不同于AS算法的状态转移规则，即由参数q0控制的伪随机比率规则。公式如下：

其中q0为给定常数，q0是[0，1]中符合均匀分布的随机数，当q≤q0时，选择的下一节点为所有可行节点中值最大的节点；当q＞q0时，V按照下面的概率转移公式Pijk(t)选择下一个节点：

其中，allowedk表示蚂蚁k可以到达的节点；α为信息启发式因子，表示轨迹的相对重要性，反映了路径上积累的信息素对后续蚂蚁选择该路径的影响程度，α越大就表示后续蚂蚁选择之前蚂蚁走过路径的可能性越大；表示边弧(i,j)的信息素浓度；β为期望启发式因子，表示能见度的相对重要性，反映了启发信息对蚂蚁路径选择的影响程度，β越大就表示该状态转移概率越接近于贪心规则；ηij(t)为启发函数，表示边弧(i,j)的能见度，公式如下：

其中，dij表示节点i与节点 j之间的距离。

在每只蚂蚁走完一步或者完成对所有节点的搜索后，对蚂蚁走过路径上的信息素及时更新以提高解的质量和算法的收敛速度[15]。ACS算法中的局部更新用于每一时刻每只蚂蚁的每一步移动之中，全局更新则是在所有的蚂蚁都完成一个周期的搜索之后对最好的搜索结果进行信息素浓度的更新。对局部和全局信息素的更新规则作如下说明：

（1）局部更新规则

每只蚂蚁从某一节点i移动到下一节点 j后，按照以下公式更新边弧(i,j)上的信息素。局部更新规则的公式为：

（2）全局更新规则

在AS中，全局更新规则是对一次循环中所有蚂蚁经过的路径进行信息素更新，而在ACS中，所有蚂蚁循环完成后才进行全局信息素更新，且只更新当前最优路径上的信息素。全局更新规则的公式：

其中，ρ为全局信息素挥发系数，1-ρ为信息素残留因子；Δτijk为本次循环中第k只蚂蚁在路径(i,j)上的信息素；Lgb为从路径构建开始到目前搜索到的全局最优路径的长度。

不仅需要算法收敛速度快，还需要算法不会过早收敛于局部最优解，这也是目前算法的矛盾方面。近年来，国内研究人员做了大量工作，以平衡算法解的多样性和收敛速度之间的关系，算法的应用范围也越来越广。在ACS算法中，启发函数只是当前节点到下一节点距离的倒数，导致蚂蚁贪图当前最短路径陷入局部最优，而本文改进算法的启发函数中引入了A*算法估价函数的思想，将方向信息考虑到算法中，从而提高算法搜索效率。

3 改进算法

3.1 改进蚁群算法启发函数

在路径规划过程中，蚁群算法因其启发函数ηij(t)仅为当前节点i与下一节点 j距离的倒数，导致蚂蚁因贪图当前最优路径而错过全局最优路径。针对蚁群算法出现的问题，本文借鉴A*算法的估价函数，将当前节点和目标点的联系引入到蚁群算法的启发函数中，对距离进行归一化处理得到：

其中，gSi为起点S到下一节点 j的实际距离；hjG为下一节点 j到目标点G的估计距离。将上述二者进行归一化处理得到gSi'和hjG'，从而使得蚁群算法的启发函数变为：

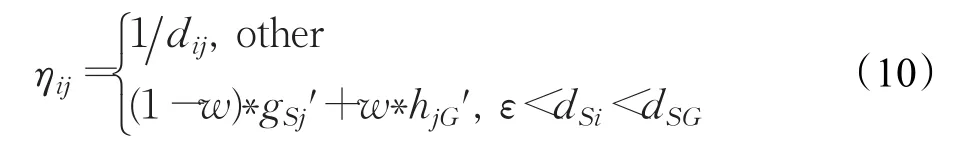
式中，dij是当前节点i和下一节点 j之间的距离；dSi是起点S和当前节点i之间的距离；dSG是起点S和目标点G之间的距离；ε为常数，它的值取决于dSG的大小。

将下一节点 j和目标点G的关系考虑到启发函数中，使得蚂蚁在搜索路径过程中更具方向性，算法的搜索空间得以减少，从而有效提高搜索效率。但是蚂蚁在移动过程中过早受到目标点方向信息的影响，初始的搜索空间太小反而会导致算法陷入局部最优。所以，在蚂蚁构建路径的初始阶段不引入方向信息，当dSi的长度大于设定阈值ε后才引入目标点的方向信息，加快算法收敛速度。

w为权值，公式如下：

其中，C为常数，w∈(0,1)。

在蚂蚁构建路径的过程中，w的值会随着下一节点到目标点的距离进行动态调整，即蚂蚁在移动过程中越接近目标点，受到的方向信息的影响越强，以提高算法搜索效率。

3.2 改进算法流程

本文应用于机器人路径规划问题的蚁群算法是在ACS算法的基础上改进而来，其伪代码形式如下：

算法参数初始化：m、α、β、ρ、τ0、NC等，将m只蚂蚁放置在起点S处。

forNC=1toNCmax

fork=1tom

初始化禁忌表；

将起点移动到禁忌表中；

判断蚂蚁k所有可行的下一节点是否已在禁忌表中；

while（存在可选下一节点蚂蚁没有走到终点）

根据A*算法的估价函数改进而来的启发函数公式（10），

然后依照公式（11）动态调整权值，蚂蚁个体根据

公式（2）和概率转移公式（3）按照概率

随机选择下一个节点 j；

更新禁忌表；

end

if下一节点 j是目标节点

记录此次迭代中每只蚂蚁从起点S到

目标点G经过的路径节点及其行走的路径长度；

end

end

记录此次迭代全局最优路径的路径长度，

按照公式（6）和（7）进行全局信息素更新；

按照公式（5）进行局部信息素更新；

end

4 实验结果及分析

为了验证改进蚁群算法的有效性，在MATLAB平台上进行了仿真实验，比较ACS算法和本文改进算法的仿真结果，并对仿真结果进行了分析。在不同复杂程度的障碍物环境（20×20，30×30，50×50）中进行仿真实验，ACS算法和本文改进算法的路径规划图以及两种算法的迭代图，分别如图1、图2、图3所示（障碍物图中的路径虚线代表ACS算法，实线代表本文算法）。

在ACS算法中，启发函数只是当前节点到下一节点距离的倒数，而本文改进算法的启发函数中引入了A*算法估价函数的思想，将当前节点和目标点的关系考虑到算法中，若在算法中过早引入方向信息，会使初始搜索空间太小从而导致算法陷入局部最优，所以本文算法在路径的后程引入目标点的方向信息，同时蚂蚁在移动过程中受到目标点的方向信息影响，此影响的大小由权值w调整。本文改进算法不仅使得蚂蚁在构建路径过程中更具方向性，算法的搜索空间得以减少，还在一定程度上提高了解的质量。

两种算法参数设置如表1所示。

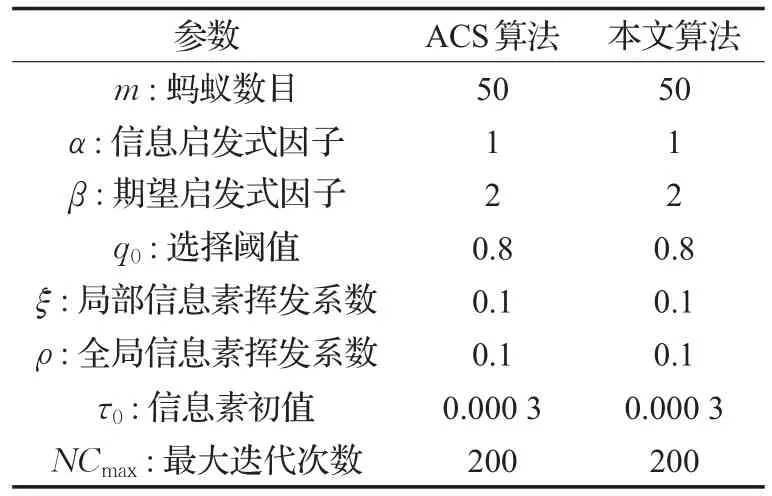
表1 参数设置

首先，本文算法选取不同的ε值在同一障碍物环境中进行20次独立实验，选取的障碍物图是图1中的20×20障碍物环境，结果如表2所示。

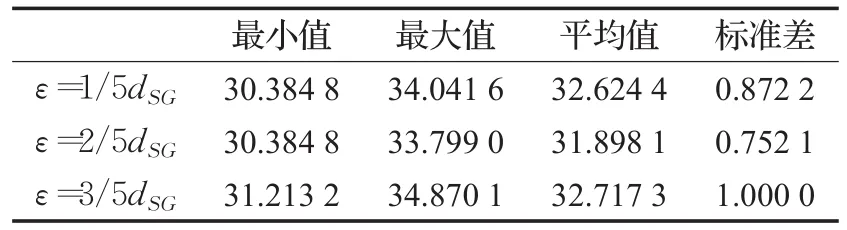
表2 同一障碍物环境不同ε值的对比实验

由表2可得，三者之中，ε=3/5dSG时得到的最小值、最大值及平均值都是最大的，在 ε=1/5dSG和ε=2/5dSG时，本文算法都得到了最优路径，而在ε=2/5dSG时，不但算法得到的平均值相比ε=1/5dSG时较小，得到的标准差也小于ε=1/5dSG时得到的标准差。综上所述，本文算法选取的ε值为2/5dSG。

本文算法和ACS算法在三种复杂度的障碍物环境下的对比实验如下所示。

图1为两种不同算法在20×20障碍物环境下的仿真结果。本文算法为了避免陷入局部最优，在蚂蚁构建路径的初始阶段启发函数中并没有引入目标点的方向信息，算法的搜索空间相对较大，在路径的后程将目标点的方向信息引用到启发函数中，减小了算法的搜索空间，加强了蚂蚁构建路径过程的方向性。因此，从以上仿真结果可以看出，本文改进算法的收敛速度高于ACS算法，得到的全局最优路径质量也明显优于ACS算法，这表明本文提出的算法是可行且有效的。

图2为两种不同算法在30×30障碍物环境下的仿真结果。ACS算法的启发函数中没有目标点的方向信息，容易出现蚂蚁贪图当前最优路径而陷入局部最优的情况；相比ACS算法，在蚂蚁所走路径的后程，本文算法在启发函数中通过加入了目标点的方向信息来影响蚂蚁对下一节点的选择，这样蚂蚁的移动过程会更具方向性，而且算法的搜索效率也会提高。仿真结果表明，障碍物环境（30×30）比图2（20×20）复杂后，ACS算法陷入了局部最优，本文改进算法的收敛速度快，并且得到的解的质量也优于ACS算法。

图3为两种不同算法在50×50障碍物环境下的仿真结果。仿真结果表明，在障碍物环境越为复杂时，本文改进算法的优势依然明显，蚂蚁在构建路径过程考虑到目标点的影响，移动过程更具方向性，算法的搜索空间小，所以本文算法收敛速度快，而且得到的解的质量也优于ACS算法。

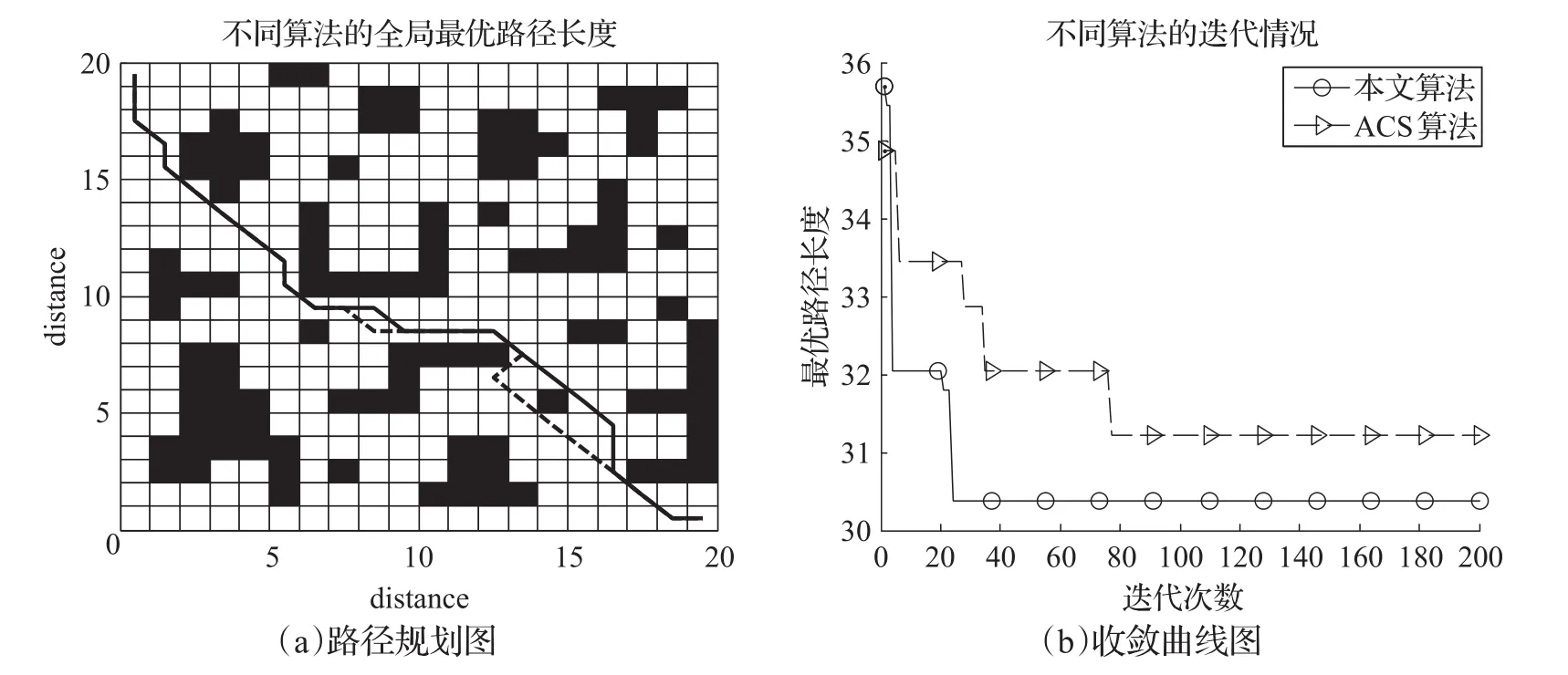
图1 障碍物环境20×20

图2 障碍物环境30×30

图3 障碍物环境50×50

对ACS算法和本文算法进行对比实验，在每个障碍物环境中运行20次得到的实验数据如表3所示。在简单的障碍物环境中本文算法的提升空间不大。但是，当障碍物环境复杂程度提高时，相比ACS算法，本文算法用更少的迭代次数得到了较好的最优路径，这表明本文算法不仅加快了收敛速度，还能在一定程度上提升解的质量。

表3 算法对比

5 结束语

传统蚁群算法在机器人路径规划中存在搜索时间较长，容易陷入局部最优等问题，针对这些问题，本文改进了ACS算法的启发函数，路径搜索初始阶段不引入目标点的方向信息；后续阶段引入目标点的方向信息，并根据下一节点到目标点的距离动态调整权值大小。实验表明，本文改进算法不仅提高了搜索效率，加快了收敛速度，还可以在一定程度上提高解的质量。针对特殊的障碍物环境（如终点处存在凹形障碍物时），本文算法权重参数的调整及阈值ε的选取还存在不足之处，后续工作将对其理论模型进行研究及完善。