基于析因设计的大数据相关关系挖掘算法
唐小川,罗 亮
(电子科技大学 计算机科学与工程学院,成都 611731)
0 引言
随着大数据时代的到来,许多数据集具有大量特征和数据记录[1],比如社交网络数据和自然语言处理数据。文献[2]指出,这种特征数量多、数据量大的数据集为大数据分析带来了巨大的挑战。对于这类数据,传统的因果关系分析可能变得十分困难,复杂度更低的相关关系分析[3]迎来了新的机遇。变量之间的相关关系是指目标变量与特征之间的关联性,文献[4]对大数据相关关系分析方法进行了综述。文献[5]指出,对于一些大数据分析问题,相关关系的结果就足以解决问题。在机器学习与数据挖掘领域,特征选择方法广泛应用于挖掘与目标变量相关的重要特征。
特征选择算法通常可分为三类[6]:嵌入式(Embedding)、封装式(Wrapper)和过滤式(Filter)。嵌入式方法将特征选择作为分类器的一个组成部分。封装式方法枚举所有特征子集,并计算其分类效果。过滤式方法通过定义一个评分标准对特征进行打分排序,最终选择得分高的特征,文献[6]提出了一个过滤式特征选择算法的框架。相比嵌入式和封装式方法,过滤式方法的效率更高并且独立于具体的分类器,因此,本文研究使用过滤式特征选择方法挖掘大数据相关关系。
文献[7]将过滤式特征选择方法分为单变量算法和多变量算法。单变量方法的效率高但是忽略特征之间的依赖性,比如信息增益(Information Gain, IG)[8]。多变量算法使用特征之间的依赖性提升了特征选择的效果,比如:文献[9]提出的互信息最大化算法考虑了相关性;文献[10]提出的一种改进的最大相关最小冗余算法考虑了条件冗余性;文献[11]提出的一种两阶段特征选择算法考虑了特征之间的交互作用,但是,多变量方法的复杂度较高,难以直接应用于大数据分析。
本文的主要内容如下:提出一种快速的多变量过滤式特征选择算法FFD(Full Factorial Design),用于挖掘大数据中与目标变量关联性强的特征和交互作用。FFD将析因设计的因子效应作为一种新的相关关系度量标准,用于度量特征和交互作用与目标变量的相关性,从而能对特征和交互作用进行统一排序,通过交互作用提升多变量过滤式特征选择算法的性能。FFD使用一种分治算法快速地从输入数据集中获取析因设计的结果,从而提高计算因子效应的速度。
1 一种大数据特征和交互作用选择方法
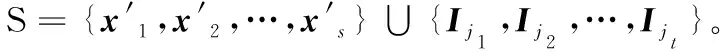
1.1 两水平完全析因设计
两水平完全析因设计FFD广泛应用于统计学实验设计(Design of Experiments, DOE),实验设计研究如何制定实验计划和分析实验结果[12]。传统的实验设计方法是一种模型驱动的方法,主要包括三个阶段:设计、测试和分析。在设计阶段,制定最有效的实验计划;在测试阶段,按照实验计划做实验;在分析阶段,使用统计学工具分析实验结果。
1.2 基于析因设计的特征和交互作用选择
文献[11]提出一种基于析因设计的特征选择算法。本文提出一个快速的搜索适合输入数据集的最优析因设计的算法,使得析因设计能够应用于大数据的特征和交互作用选择。式(1)是析因设计的统计模型。该模型是一个包含交互作用项的一般线性模型(General Linear Model, GLM)。
f(x1,x2,…,xp)=β1x1+β2x2+β3x3+…+β12x1x2+β13x1x3+…+β123x1x2x3+…+ε
(1)
其中:x1,x2,x3,…表示特征;x1x2,x1x3,x1x2x3,…表示交互作用;ε表示随机误差。特征和交互作用常被称为因子。
式(1)中的系数β表示因子与目标变量之间的关联性,常被称为因子效应。对于给定的特征,如果该特征的因子效应的绝对值大于其他因子,那么该特征与目标变量之间的相关关系最强。因此,本文使用因子效应作为特征与目标变量之间关联性的度量标准。
本文提出一种快速计算因子效应的方法,该方法是一种数据驱动的方法,克服了由模型驱动的析因设计方法需要手动执行实验的局限性。该方法也说明了为输入数据集搜索最优析因设计的过程,具体如下:
1)用特征排序方法对X中的所有特征进行排序,比如对称不确定性[13]和最大互信息[9]。
2)将X中的所有特征都转化为二值变量,比如:对于连续性特征,使用该特征的均值将其划分为高(+1)和低(-1)两个水平。这个过程常被称为二值化。
3)计算最大的两水平析因设计,使得数据集D能够为其提供足够的数据。由于析因设计与因子数量一一对应,本文提出一个搜索最大析因设计对应的最大因子数量的算法:
输入:数据集D,其中的特征已经排序和二值化。
输出:最大因子数量k。
index[0]←{1,2,…,n}
k← 1
while true do
析因设计的行的数量nrun← 2k
k←k+1
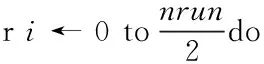
//将index[i]划分为两部分:
temp_index[2i] ← 找出所有的s0∈index[i],
满足D[s0][k]==-1
temp_index[2i+1]← 找出所有的s1∈index[i],
满足D[s1][k]==1
end for
iftemp_index中有元素为空 then
break
else
index←temp_index
end if
end while
该算法使用分治法搜索最大析因设计对应的特征数量k,避免了将数据集D与特征数量为1到k的所有析因设计进行比较,因此,该算法能快速地找出适合数据集D的最大析因设计。
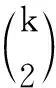
①生成单个特征mi,i∈{1,2,…,k}。mi的值开始于-1,然后切换为1,…,依此类推,每隔N/2i个元素切换一次正负号。
…
③构造k阶交互作用m2k。令m2k=mi1·mi2·…·mik。
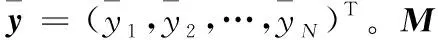
因此,可以通过式(2)计算因子效应,其中wi(i∈{1,2,…,k})是mi的权重系数,表示单个特征的因子效应;wj(j∈{k+1,k+2,…,N})是mj的权重,表示交互作用的因子效应,从而可以通过因子效应对特征和交互作用进行统一排序。
(2)
下面举例说明如何使用FFD分析两个因子x1、x2和交互作用x1x2。
在设计阶段,生成一个设计矩阵,如表1的左侧3列所示,得到设计矩阵M如下:

(3)
在测试阶段,为每一个实验随机产生两个响应值,如表1右侧两列所示。
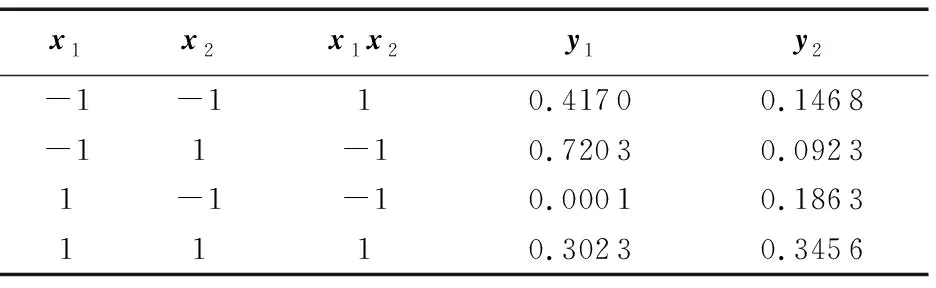
表1 二因子析因设计的设计矩阵和响应值
在分析阶段,计算各个特征和交互作用的因子效应。由表1右侧2列的每一行分别求平均值可得平均响应值为:
(4)
因此,根据式(2)可得因子效应为:
(5)
从而x1,x2和x1x2的因子效应分别为-0.271 1,0.355 2和0.106 3。按因子效应绝对值的大小可将特征和交互作用排序为:
x2>x1>x1x2
(6)
1.3 计算复杂度分析
输入数据D∈Rn×p由n条记录和p个特征组成,适合数据集D的最大的两水平析因设计由k个因子组成,k的上界为O(lbn)。
搜索最大析因设计的复杂度为O(2nk),即O(2nlbn)。
2 实验与分析
本文通过实验对比了FFD与其他特征选择方法。实验采用3个UCI(University of California Irvine Machine Learning Repository)数据集,包括细颗粒物数据集(Beijing Particulate Matter 2.5,PM2.5)、垃圾邮件数据集(Spambase)和文本分类数据集(Baseball vs. Hockey, BASEHOCK)。由于本文提供的方法已经显式地考虑了交互作用,所以通过线性回归的分类错误率对比不同的特征选择方法。本文对比了3个著名的过滤式特征选择算法:联合互信息最大化(Joint Mutual Information Maximisation, JMIM)算法[14]使用联合互信息度量两个特征和一个目标变量三者之间的交互作用;ReliefF[15]是一种基于相似度的特征选择算法,利用了特征之间的条件依赖性;互信息最大化(Mutual Information Maximisation, MIM)算法[9]考虑了单个特征与目标变量之间的相关关系。
本文的实验配置[16]如下。首先,使用十折交叉验证将数据随机划分为训练数据和测试数据。然后对数据进行二值化。其次,用特征选择方法选择k={2,4,…,50}个特征或交互作用,并更新数据集。交互作用的值可由向量的对应分量的乘积得到,可视为一个新特征。再次,用训练数据训练线性回归模型,然后用得到的模型在测试数据上得到分类错误率。最后,计算十折交叉验证的平均分类错误率。
Spambase数据集。该数据集由4 601条记录和57个特征组成。图1是Spambase数据集上的实验结果。FFD的错误率一直低于其他对比方法。FFD的最低错误率是9.06%,其他方法的最低错误率是11.89%,FFD将错误率降低了2.83个百分点。一个可能的原因是FFD选择的交互作用具备单个特征所不具备的信息,比如二阶交互作用x7x53。
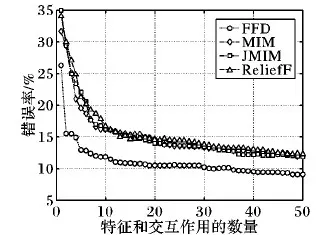
图1 Spambase数据集上的分类错误率随特征数量的变化
PM2.5数据集。该数据集记录了北京市在2010至2014年间的PM2.5数据,由43 824条记录和13个特征组成。在进行特征选择之前,本文将PM2.5数据集的特征和目标变量离散化为二值变量。对于连续型变量,使用其平均值将其离散化为二值变量,将高于平均值的项标记为1,低于平均值的项标记为-1。对于一些离散型变量,使用一对多(one-vs-all)分解策略将其离散化为二值变量。对于时间特征,每年(year)被离散化为四个季度,每个月(month)被离散化为两个半个月,每天(day)被离散化为两个半天。对于风向特征“wind direction”,离散化为东北(North East, NE)、西北(North West, NW)、东南(South East, SE)和和静风(Calm and Variable wind, CV)。对于目标变量,设定PM2.5的阈值为75,PM2.5大于75 μg/m3表示空气受到污染,记为1,否则记为-1。因此,经过离散化以后,得到21个二值变量特征。
图2是PM2.5数据集上的实验结果。可以看到,随着已选特征和交互作用数量的增加,FFD的错误率逐渐降低,当特征和交互作用大于12时,FFD的错误率持续低于其他对比方法。FFD的最低错误率为32.72%,低于其他对比方法的最低错误率(33.61%)。一个可能的原因是FFD选择的交互作用具有其他特征所不具备的关键信息,比如:交互作用x6x8(风速和东南风之间的交互作用)的重要性排第三,可能对北京PM2.5有显著的影响。
BASEHOCK数据集。该数据集由1 993条记录和4 862个特征组成。图3是BASEHOCK数据集上的实验结果。FFD的错误率一直低于对比方法,FFD将最低错误率降低了5.07个百分点。一个可能的原因是FFD选择的交互作用(比如二阶交互作用x2965x3302)具备其他方法所忽略的关键信息。
表2对比了FFD与其他算法的分类错误率。FFD分别将MIM、JMIM和ReliefF的平均错误率降低了2.95、3.33和6.62个百分点。FFD在Spambase、PM2.5和BASAHOCK数据集上的最低错误率都低于对比方法。
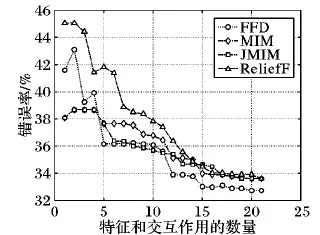
图2 PM2.5数据集上的分类错误率随特征数量的变化
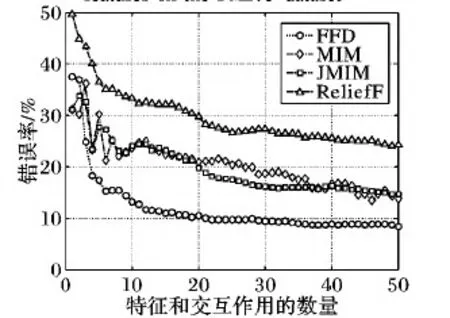
图3 BASEHOCK数据集上的分类错误率随特征数量的变化
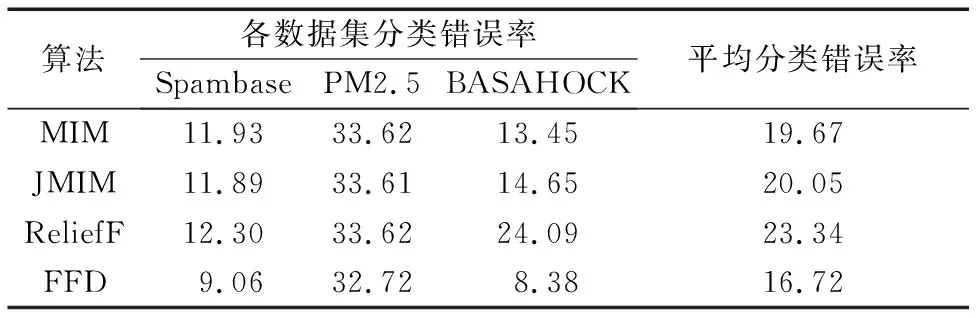
Tab. 2 Comparison of lowest classification error rate for each feature selection algorithm %
3 结语
本文提出了一种新的过滤式特征选择方法FFD用于大数据相关关系分析。FFD使用析因设计的因子效应作为特征与目标变量之间的关联性的度量标准。提出一种为输入数据集快速搜索最佳析因设计的分治算法,理论分析表明,这个分治算法的复杂度为O(lb2n),有效降低了计算因子效应的复杂度。为了对特征和交互作用进行统一排序,FFD将因子效应作为排序标准。
实验结果表明,FFD在数据集BASEHOCK、Spambase和PM2.5数据集上的最低错误率分别比其他对比方法低5.07、2.83和0.89个百分点,也就是将实验中的所有数据集的最低错误率降低了2.93个百分点。FFD成功地发现了影响PM2.5数据集的一个关键因素是风速与风向的交互作用,即东南方向的风速可能对北京PM2.5有重要影响。

