基于特征变权的动态模糊特征选择算法
王 玲 孟建瑶
(北京科技大学自动化学院 北京 100083) (工业过程知识自动化教育部重点实验室(北京科技大学) 北京 100083) (lingwang@ustb.edu.cn)
特征选择是数据挖掘和机器学习中的一个重要课题,它不仅有助于理解数据、节约计算成本、减少特征之间的相互影响,而且可以提高预测的准确率[1-2].特征选择也称特征子集选择,是指从原始特征中选择出一些最有效特征以降低数据集维度的过程[3].目前,特征选择已经应用于多个领域,例如工业传感器数据分析[4]、空气质量分析[5]、健康数据分析[6]等等.
在一些现实的系统中,人们往往利用一些模糊语义将原始特征集转化为模糊特征集,提高系统的可解释性.然而,模糊化后的特征空间比原始的特征空间维度更高,为了减少系统模糊化后的复杂性,从模糊特征中选择有价值的特征显得更为重要.此外,实际应用往往是具有多特征的动态复杂系统,随着时间的变化,特征的重要程度也在逐渐发生变化,例如一些重要的特征随着时间的推移变得冗余,或者起初不重要的特征随着时间的推移变得越来越重要.虽然国内外已经涌现了一系列特征选择算法,例如过滤式特征选择算法[7]、封装式特征选择算法[8]、嵌入式特征选择算法[9]等用于提高学习算法的性能.但上述方法不能体现特征选择的实时性,导致算法延迟和不连续,影响了可解释性.因此,动态特征选择算法应运而生.文献[10]提出基于在线分类器的动态特征选择算法,该算法选择所有可以代表整体数据集信息的特征,但利用分类器评估所选特征的好坏,增加了计算负担;文献[11]提出基于贝叶斯分类器的封装式动态特征选择算法,该算法利用贪婪算法寻找最优的特征子集,增加了算法的时间复杂度和空间复杂度;文献[12]介绍了4种新的特征质量检测指标,然后用检测指标和聚类算法动态地选择有用的特征,但是聚类算法需要人为设置聚类个数,降低了算法的自适应性;文献[13]提出基于K均值算法和遗传算法的动态特征选择算法,该算法分别利用遗传算法和K均值算法确定目标函数和寻优范围,但该算法得到的特征子集不是全局最优的.尽管如此,针对动态系统,如何自适应地进行模糊特征选择仍然是一个挑战性的课题.
本文主要有4个方面的贡献:
1) 提出一种基于特征变权的动态模糊特征选择算法,包括离线模糊特征选择和在线模糊特征选择2部分;
2) 通过计算每个模糊特征的权重,动态优化所选模糊特征子集,保证了特征选择过程的平滑性和时效性;
3) 在特征变权的基础上,离线模糊特征选择利用后向选择算法和模糊特征筛选指标获得优化模糊特征子集,在线模糊特征选择根据重要度不断更新优化模糊特征子集;
4) 应用不同数据集的实验结果表明:我们提出的动态模糊特征选择算法在无需设置任何参数的情况下,提高了算法的自适应性和预测准确性.
1 相关工作
动态特征选择算法的目的是在动态数据集中选择出能够实时刻画主要特性的特征.关于动态特征选择的研究有很多[14-18],其中,一些动态特征选择算法只能处理类别数据,例如文献[14]提出基于粗糙集的动态特征选择算法,以粗糙集为基础,动态地计算特征的独立性,从而进行特征选择;文献[15]提出基于邻域粗糙集的动态特征选择算法,邻域粗糙集摆脱了粗糙集只能处理离散型数据的约束;文献[16]提出基于信息粒度的动态特征选择算法,利用非矩阵的信息粒度结构减少了算法时间和空间的消耗,提高了算法效率.然而,上述算法都是针对类别数据集,适用范围较小.除此之外,研究者提出一些针对其他类型数据集的动态特征选择算法;文献[17]提出动态无监督特征选择算法,该算法将特征选择直接嵌入聚类算法中,利用聚类算法保存局部信息结构,帮助选择具有辨识能力的特征,然而,该算法需要设置参数控制聚类算法目标函数的构建,导致算法自适应能力不佳;文献[18]提出新的无监督动态特征选择算法,该算法近似地保存数据,根据在近似数据上的回归结果确定特征的重要程度,从而进行特征选择.然而,该算法依赖回归模型进行特征选择,没有独立的特征评价指标,限制了算法的使用范围.
针对模糊数据的特征选择算法较少,文献[19]提出基于最小-最大学习规则和扩展矩阵的模糊特征选择算法,利用模糊化后的数据构建扩展矩阵,根据最小-最大学习规则衡量每个模糊特征包含重要信息的多少,从而获得模糊特征选择结果,但是此算法只适用于静态数据集,不适用于动态系统中的模糊特征选择;文献[20]提出基于在线特征权重的动态模糊特征选择算法,该算法计算每个模糊特征的权重,根据可分离判据,选择有助于分类的模糊特征,然而该算法中需要设置分离阈值,降低了算法的自适应能力.
鉴于此,本文提出了基于特征变权的动态模糊特征选择算法(dynamic fuzzy features selection based on variable weight, DFFS-VW).主要包括2个阶段:
1) 离线模糊特征选择.首先,利用滑动窗口分割模糊数据,在第1个滑动窗口中进行离线模糊特征选择,计算每一个模糊输入特征与输出特征的互信息量;然后根据互信息量计算每一个模糊输入特征的权重,并从大到小排序,计算相邻模糊输入特征的权重梯度和截断点阈值进而获得候选模糊特征子集,缩小了寻找最优模糊输入特征子集的空间,提高了算法效率;在此基础上,根据模糊特征筛选指标既考虑模糊特征子集的输入特征与输出特征之间的互信息量又兼顾模糊输入特征之间的互信息量来筛选特征,并通过后向特征选择算法得到离线的优化模糊特征子集,保证了所选模糊特征子集为全局最优.
2) 在线模糊特征选择.在依次到来的滑动窗口中进行在线模糊特征选择,综合利用当前时刻滑动窗口中的候选模糊特征子集和前一个滑动窗口中的优化模糊特征子集,自适应地跟踪输入模糊特征权重的变化,得到当前滑动窗口中的优化模糊特征子集,提高了模型的解释性并保证学习的平滑性和实效性;根据模糊输入特征与初始化优化模糊特征子集之间的重要度获取最终的优化模糊特征子集,同时考虑历史特征选择结果和当前数据分布,确保最终的优化模糊特征子集的优越性.在DFFS-VW算法中,输出特征可以是类别标签,也可以是连续数据,无论是离线模糊特征选择,还是在线模糊特征选择,都无需依赖分类器或者回归模型,无需人为设置任何参数,提高了算法的自适应性.
2 相关定义
本文以滑动窗口分割模糊化数据为基础,从模糊特征互信息量入手,建立起模糊输入特征与输出特征之间的联系,进而实现动态模糊特征选择.为了确定滑动窗口的大小,这里采用Hoeffding边界检测数据的分布.
定义1. Hoeffding边界[21].对于取值范围为R的特征,假设每个滑动窗口包含n条数据样本,在置信程度是1-δ(δ一般取0.05)的条件下,Hoeffding边界ε为
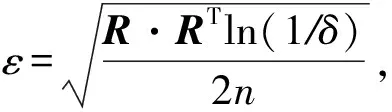
(1)
其中,R为特征的取值范围:
R=(x1.max-x1.min,x2.max-x2,min,…,
xj,max-xj,min,…,xL,max-xL,max),
其中,xj,max是第j个变量的最大值,xj,min是第j个变量的最小值,L是数据集变量的个数.
随着n的增加,Hoeffding边界ε在变小,这表明当n足够大,Hoeffding边界ε将趋近于0.
根据Hoeffding边界,样本集的最小容量NH可以确定:

(2)
根据式(2)可知,Hoeffding边界ε是获得样本集的最小容量NH的关键.假设相邻滑动窗口Wp-1和Wp所包含的样本集均值分别是μp-1和μp,在置信程度是1-δ的条件下,|μp-1-μp|≤2ε,则样本集的最小容量NH的计算公式可以调整为

(3)
由于对数值数据进行模糊化处理不仅有助于提取高层次的含义,而且不需要对数据进行简单地“硬”划分,它被广泛应用于智能系统中[19].通常的模糊化方法是根据经验或者知识建立隶属度函数.但是,在多数情况下,很难获取所需要的信息或者专家知识.本文利用以前的研究基础[22]对数据特征进行聚类实现特征模糊化.设第p(p≥0)个滑动窗口包含n条数据,L维输入特征和一维输出特征,可以表示为
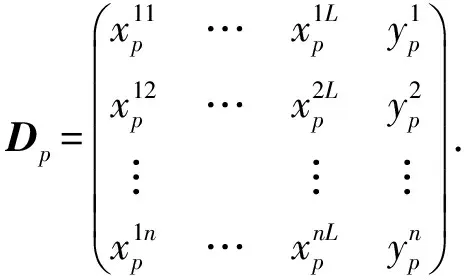
(4)


(5)

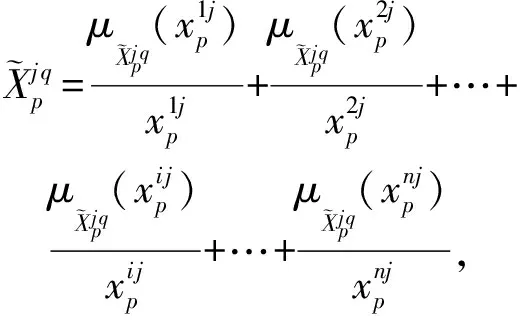
(6)
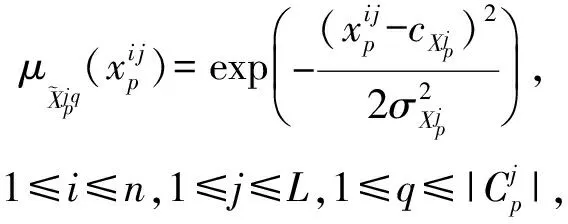
(7)

为了度量模糊特征之间的相关性,有必要引入新的度量.

(8)
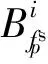
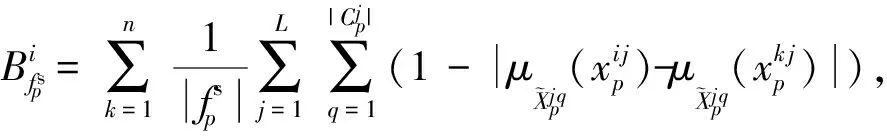
(9)
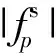

(10)
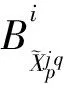
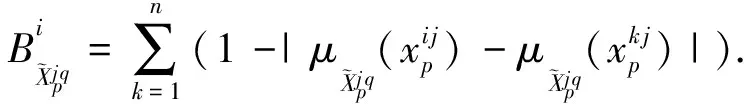
(11)
3 基于特征变权的动态模糊特征选择算法(DFFS-VW)
3.1 DFFS-VW算法框架
为了提高模糊动态特征选择的实效性和快速性,降低算法复杂性,发现各个模糊输入特征权重的演化规律.本文提出了DFFS-VW算法,该算法的基本框架如图1所示,首先利用滑动窗口W0,W1,…,Wp分割模糊数据,以第1个滑动窗口中的数据作为初始数据进行离线模糊特征选择,在随后依次到来的滑动窗口中进行在线模糊特征选择.在离线模糊特征选择中,计算每个模糊输入特征的权重,根据权重得到候选模糊特征子集;结合后向特征选择算法和模糊输入特征筛选指标迭代地筛选候选模糊特征子集,每一步都忽略其中权重值最小的模糊特征,得到优化模糊特征子集.在在线模糊特性选择中,根据当前滑动窗口中的数据获取候选模糊特征子集,利用上一个滑动窗口的模糊优化特征子集与当前窗口的候选模糊特征子集的交集作为当前快照的初始优化模糊特征子集,计算其余的模糊输入特征与初始优化模糊特征子集的重要度,若重要度大于0,将模糊输入特征加入优化模糊特征子集.最后,根据各个模糊输入特征的权重对模糊输入特征进行演化分析.
3.2 滑动窗口的确定
在动态环境中,滑动窗口是一种被广泛应用的技术.每个滑动窗口中包含着最新产生的样本,并丢弃过去的样本.目前主要有2种确定滑动窗口的方法:1)使用固定的窗口大小;2)根据衰减因子确定滑动窗口中丢弃的数据和保留下来的数据,利用新数据代替已丢弃的数据.这2种方法都需要人为设置参数,然而,这些参数都很敏感,不易确定.根据数据分布直接确定窗口大小,可以解决上述问题.Hoeffding边界考虑了特征的变化范围,不断地调整滑动窗口包含的样本个数n,使得通过滑动窗口中的数据求得的最小容量NH不大于实际滑动窗口样本个数n,将n作为固定的滑动窗口大小.在动态特征选择过程中,随着信息不断的采集输入,滑动窗口的任务是以有效的方式管理输入数据,存储信息.相邻滑动窗口记录将被用来进行演化过程中特征之间的对等比较,获取各个输入模糊特征对输出特征的权重演化规律.

Fig. 1 Framework of the DFFS-VW图1 DFFS-VW框架
3.3 模糊特征权重
模糊特征权重是衡量模糊特征重要性的一种指标,在区间[0,1]中连续变化.模糊特征权重越接近1,代表该模糊特征越重要;越接近0,表示模糊特征重要性越低.模糊特征权重具有柔软性和平滑性:柔软性是指权重可以变小,但是不能完全丢弃,具有低模糊特征权重的特征仍然含有较少的信息;平滑性是指模糊特征权重在连续不断地变化,因此,具有低模糊特征权重的特征在之后的学习中仍有可能变成重要的特征.利用模糊特征权重的这2个特性,对模糊特征进行动态特征选择.本文根据互信息量计算每个模糊特征的权重:
(12)

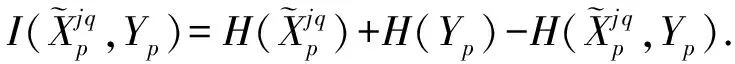
(13)
当Yp是类标签时,Yp的熵H(Yp):
(14)

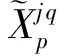
(15)
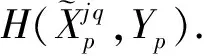

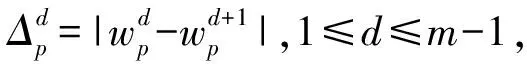
(16)
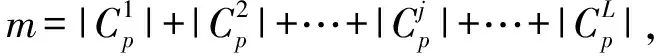
(17)

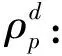
(18)
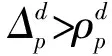
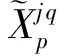
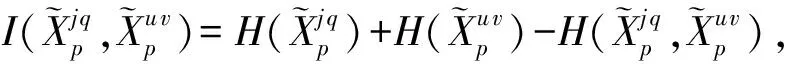
(19)
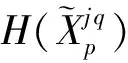
为此,我们将模糊输入特征筛选指标FCI作为衡量动态模糊特征选择的衡量标准.它不仅考虑模糊特征子集的输入特征与输出特征之间的互信息量,还考虑模糊输入特征与模糊输入特征之间的互信息量:

(20)
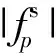
(21)
(22)
3.4 离线模糊特征选择
第1个滑动窗口中的数据作为初始数据进行离线模糊特征选择,主要分为2部分:1)根据输入模糊特征和输出特征的互信息量计算各个输入模糊特征的权重,将模糊输入特征根据权重由大到小排序,获取候选模糊特征集;2)在候选模糊特征集中,根据模糊特征筛选指标同时考虑输入模糊特征和输出特征的互信息量与输入模糊特征之间的互信息量,利用后向特征选择和模糊输入特征筛选指标得到与输出特征相关性最大、冗余度最小的优化模糊特征子集.
算法1. 离线模糊特征选择算法.
输入:所有模糊特征;
输出:最优模糊特征子集.
Step2.1. 分别计算各个模糊特征与输出类别的互信息量.
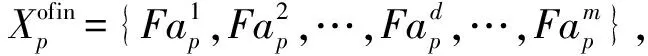


3.5 在线模糊特征选择

算法2. 在线模糊特征选择算法.
输入:前一个滑动窗口的聚类结果和当前滑动窗口的所有数据;
输出:优化模糊特征子集.

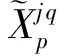
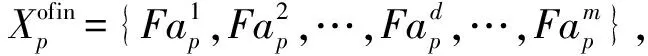

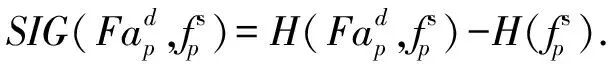
(23)
Step5. 选择具有最大重要度的模糊特征.选择满足下面条件的属性:

(24)
3.6 DFFS-VW算法计算复杂度分析
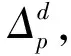
在线模糊特征选择获取当前窗口的候选模糊特征集的过程与离线模糊特征选择的相似,最坏情况下所需要的时间复杂度是O(m+m+m+m);最好情况下所需要的时间复杂度是O(m+m+m+3),在此基础上,依次计算其余的模糊特征相对于候选模糊特征集的重要度,直到其重要度不大于0,获得最终的优化模糊特征子集,最坏情况下,所需要的计算复杂度数O(m-3).综上所述,该算法的复杂度是O(4m),经化简算法的最终复杂度是O(m).
4 实验结果
4.1 实验环境
本文将DFFS-VW算法与基于邻域粗糙集的动态特征选择算法(incremental feature selection based on fuzzy neighborhood rough set, IFSFNRS)[13]、基于贝叶斯分类器的封装式动态特征选择算法(wrapper feature selection algorithm with incremental Bayesian classifier, WFSIBC)[11]、动态无监督特征选择算法(online unsupervised multi-view feature selection, OMVFS)[20]、改进的动态无监督特征选择(feature selection on data streams, FSDS)[20]对比,选取1个人工合成数据集、UCI数据库中的10个数据集[23]、2个分类数据流[24]和2个回归数据流作为实验数据进行分析,以测试DFFS-VW算法在无需设置任何参数的情况下,算法执行效率、自适应和预测准确性方面均得到提高.对于所有数据,各个维度均进行输入特征模糊化处理,使得数据集中所有数据值均在[0,1]区间.所有实验都在Inter®CPU 2.30 GHz工作台上运行,利用matlab 2014.a软件进行仿真.数据集的详细信息如表1所示:
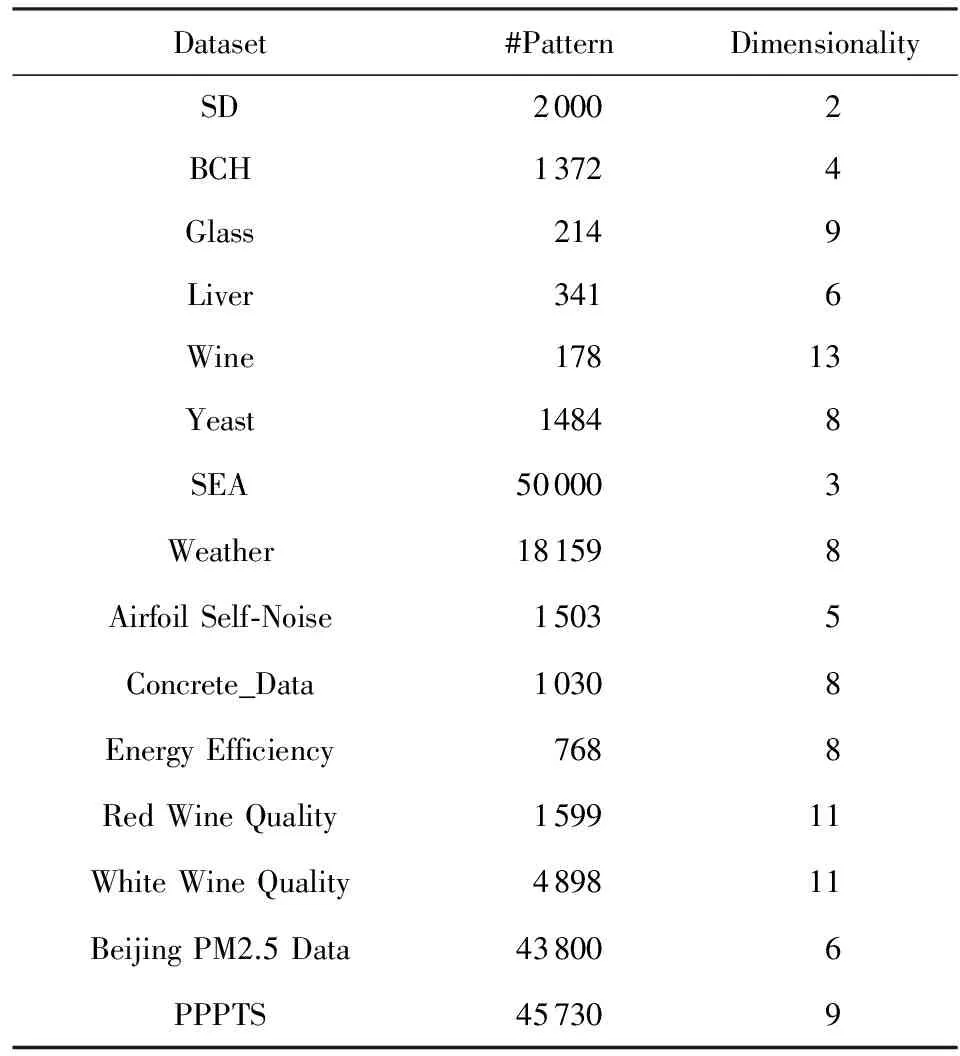
Table 1 Description of Datasets表1 数据集描述
4.2 评价指标
本文采用2种评价指标对算法的动态特征选择效果进行评价:分类准确率(Acc)和平均绝对百分比误差(MAPE).
(25)
其中,ak代表第k个类别中算法的分类结果和实际数据集分类情况相一致的数据个数,|C|是类别个数,n是数据集中包含的数据个数.
(26)
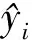
4.3 滑动窗口对特征选择结果的影响测试
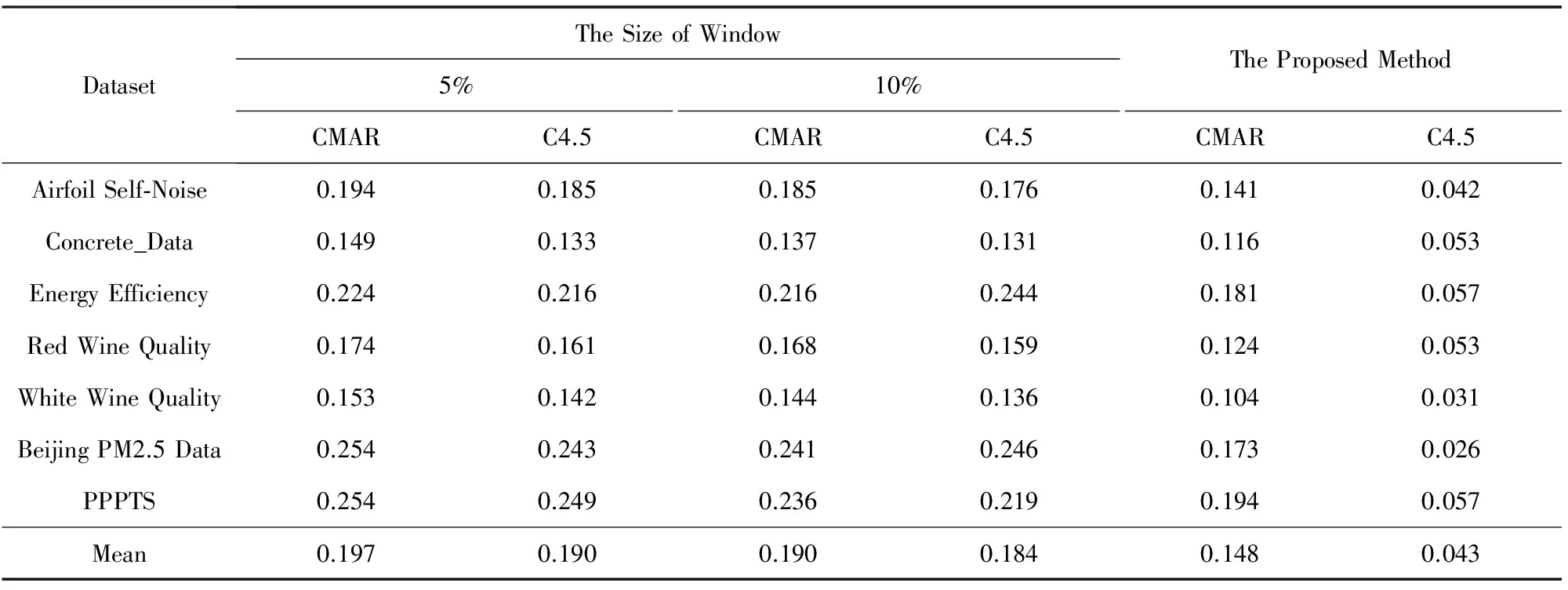
为了分析滑动窗口大小对DFFS-VW算法模糊特征选择结果的影响,本文利用不同数据集形成大小各异的滑动窗口,以数据集70%作为训练集,30%作为测试集,分析比较模糊特征选择的性能.表2分别对比了CMAR(classification based on multiple association rules)分类器[25]、C4.5分类器[26]和DFFS-VW算法对不同大小滑动窗口的模糊特征选择结果的分类性能,其中CMAR中的最小支持度设置为10%,最小置信度为70%,C4.5选取信息增益最大的作为划分节点.从表2可以看出,本文所提方法自动确定窗口大小的分类性能优于人为定义窗口大小的分类性能.表3分别对比了BP神经网络[27]、支持向量回归(support vector regression, SVR)[28]和DFFS-VW算法对不同大小滑动窗口的模糊特征选择结果的预测性能,其中BP神经网络有1层隐含层,隐含层中包含10个节点.SVR的核函数为径向基函数,不敏感系数为0.05,惩罚因子为10.从表3可以看出,本文所提出方法的预测结果优于人为定义窗口大小的预测结果.这是由于本文所提出的窗口大小确定方法根据Hoeffding边界考虑了数据的分布情况,提高了分割后的模糊数据的分类性能和预测性能.
Tabel 2 The Comparison of the Classification Accuracy(Acc) for CMARC4.5 on Different Window Sizes表2 不同窗口大小的CMARC4.5分类性能(Acc)对比
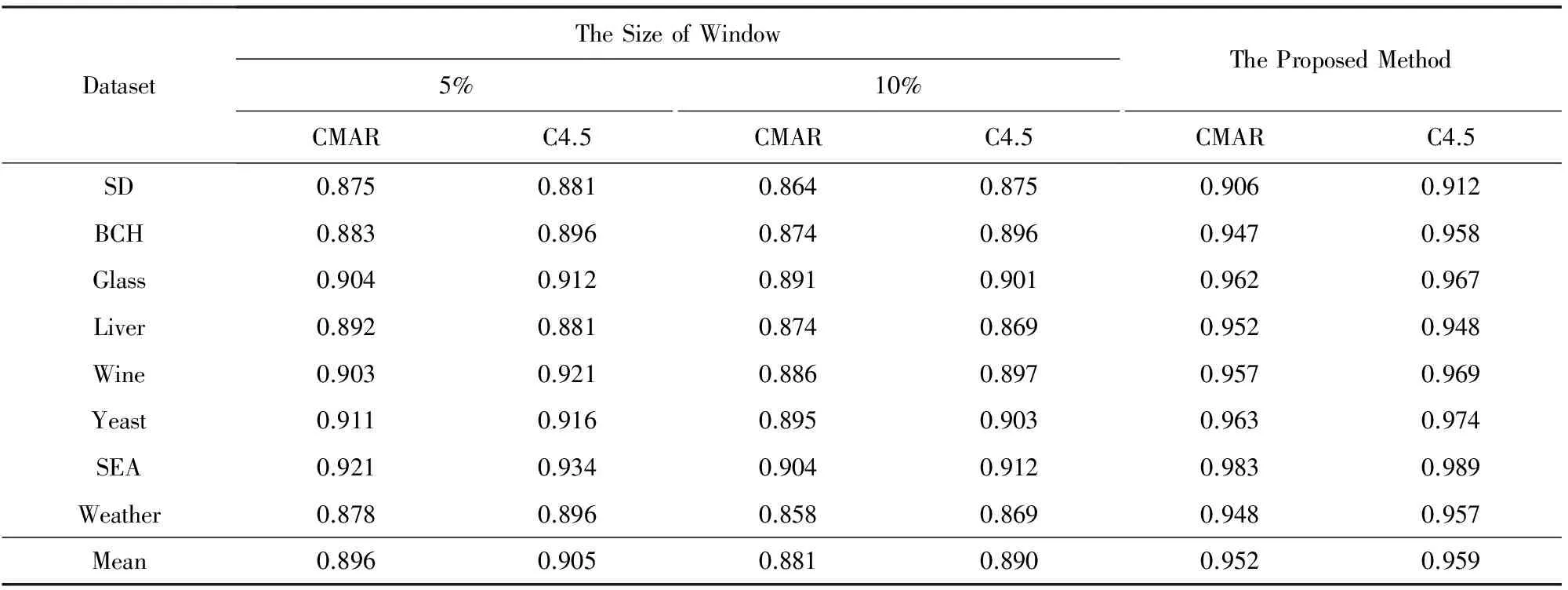
Tabel 2 The Comparison of the Classification Accuracy(Acc) for CMARC4.5 on Different Window Sizes表2 不同窗口大小的CMARC4.5分类性能(Acc)对比
DatasetTheSizeofWindow5%10%CMARC4.5CMARC4.5TheProposedMethodCMARC4.5SD0.8750.8810.8640.8750.9060.912BCH0.8830.8960.8740.8960.9470.958Glass0.9040.9120.8910.9010.9620.967Liver0.8920.8810.8740.8690.9520.948Wine0.9030.9210.8860.8970.9570.969Yeast0.9110.9160.8950.9030.9630.974SEA0.9210.9340.9040.9120.9830.989Weather0.8780.8960.8580.8690.9480.957Mean0.8960.9050.8810.8900.9520.959
Tabel 3 The Comparison of the Prediction Accuracy(MEAP) for BPSVR on Different Window Size表3 不同窗口大小的BPSVR预测性能(MEAP)对比
Tabel 3 The Comparison of the Prediction Accuracy(MEAP) for BPSVR on Different Window Size表3 不同窗口大小的BPSVR预测性能(MEAP)对比
DatasetTheSizeofWindow5%10%CMARC4.5CMARC4.5TheProposedMethodCMARC4.5AirfoilSelf⁃Noise0.1940.1850.1850.1760.1410.042Concrete_Data0.1490.1330.1370.1310.1160.053EnergyEfficiency0.2240.2160.2160.2440.1810.057RedWineQuality0.1740.1610.1680.1590.1240.053WhiteWineQuality0.1530.1420.1440.1360.1040.031BeijingPM2.5Data0.2540.2430.2410.2460.1730.026PPPTS0.2540.2490.2360.2190.1940.057Mean0.1970.1900.1900.1840.1480.043
4.4 特征选择效果测试
为了充分验证DFFS-VW算法的有效性,对比WFSIBC算法、IFSFNRS算法、OMVFS算法和FSDS算法在多个数据集下的特征选择效果.图2给出5种特征选择算法的模糊特征选择结果与原始模糊特征个数的对比结果.从图2可以看出,除数据集SD,经过5种动态特征选择算法后,所选模糊特征个数都比原始模糊特征个数少,算法DFFS-VW最为明显.DFFS-VW算法所选的模糊特征个数均比其余4种算法的少,这是因为DFFS-VW算法根据模糊权重获取候选模糊特征子集,同时考虑输入模糊特征与输出特征的互信息量与输入模糊特征之间的互信息量得到最优模糊特征子集,使得DFFS-VW算法的特征选择效果更加明显.

Fig. 2 Fuzzy features comparison of different agorithms on different datasets图2 模糊特征个数对比
表4给出了CMAR分类器和C4.5分类器对原始模糊特征集和3种动态特征选择算法的所选模糊特征集的分类准确性的对比.从表4可以看出,除了SD数据集,DFFS-VW算法所选的模糊特征子集对于CMAR分类器的分类效果最好;经特征选择后,C4.5分类器对于各个数据集的分类准确率均得到了提高,其中DFFS-VW算法所选的模糊特征子集提高得最明显.
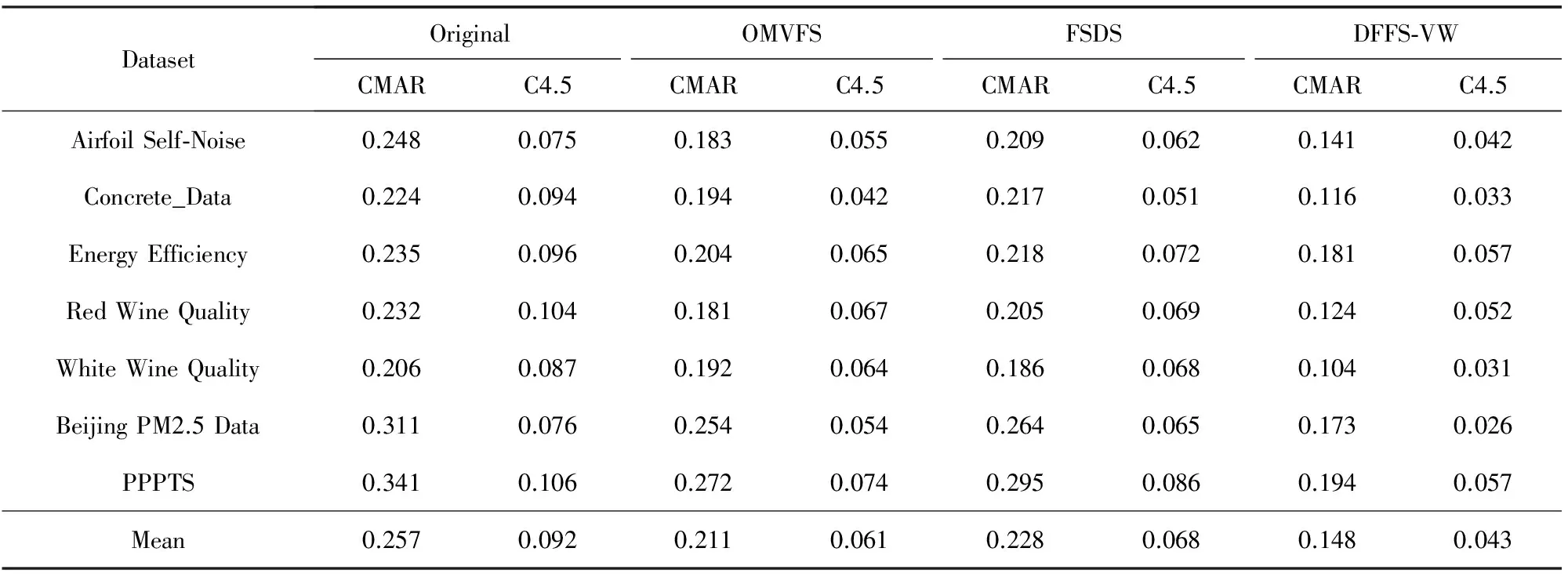
表5给出了BP神经网络和支持向量回归对原始模糊特征集和3种动态特征选择算法的所选模糊特征集的预测精确性的对比.从表5可以看出,除SD数据集外,BP神经网络对DFFS-VW算法所选的模糊特征子集的预测精确性最好;经模糊特征选择后,支持向量回归对于各个数据集的预测精确性均得到了提高,其中DFFS-VW算法所选的模糊特征子集提高得最明显.
Tabel 4 The Comparison of the Classification Accuracy(Acc) 表4 CMARC4.5分类性能(Acc)对比

Tabel 4 The Comparison of the Classification Accuracy(Acc) 表4 CMARC4.5分类性能(Acc)对比
DatasetOriginalWFSIBCIFSFNRSDFFS⁃VWCMARC4.5CMARC4.5CMARC4.5CMARC4.5SD0.9060.9120.9060.9120.9060.9120.9060.912BCH0.9210.9250.9400.9450.9360.9380.9470.958Glass0.9320.9060.9510.9580.9450.9490.9620.967Liver0.9160.8960.9320.9330.9280.9310.9520.948Wine0.9250.9130.9390.9360.9380.9320.9570.969Yeast0.9150.9240.9430.9460.9280.9350.9630.974SEA0.9230.9090.9560.9610.9440.9250.9830.989Weather0.9190.9180.9450.9430.9360.9280.9480.957Mean0.9200.9130.9390.9420.9330.9310.9520.959
Tabel 5 The Comparison of the Prediction Accuracy (MEAP) 表5 BPSVR预测性能(MEAP)对比
Tabel 5 The Comparison of the Prediction Accuracy (MEAP) 表5 BPSVR预测性能(MEAP)对比
DatasetOriginalOMVFSFSDSDFFS⁃VWCMARC4.5CMARC4.5CMARC4.5CMARC4.5AirfoilSelf⁃Noise0.2480.0750.1830.0550.2090.0620.1410.042Concrete_Data0.2240.0940.1940.0420.2170.0510.1160.033EnergyEfficiency0.2350.0960.2040.0650.2180.0720.1810.057RedWineQuality0.2320.1040.1810.0670.2050.0690.1240.052WhiteWineQuality0.2060.0870.1920.0640.1860.0680.1040.031BeijingPM2.5Data0.3110.0760.2540.0540.2640.0650.1730.026PPPTS0.3410.1060.2720.0740.2950.0860.1940.057Mean0.2570.0920.2110.0610.2280.0680.1480.043
如图3所示,本文采用不同的数据集对5种不同算法的运行时间进行了对比,可以看出,针对同一个数据集,DFFS-VW算法的运行时间最短.由于FSDS算法利用回归模型提高所选模糊子集的预测正确率,在回归模型寻参期间需要不断迭代,时间复杂度大约为O(n3);WFSIBC算法使用贪婪算法发现最优特征子集,而贪婪算法的时间复杂度是O(nlogn),当数据量较大时,算法复杂度也会大幅度地增加;IFSFNRS算法以粗糙邻域为基础,在最坏情况下,需要对整个数据集进行重新特征选择,时间复杂度不低于O(logn2);OMVFS算法将特征选择嵌入到聚类算法中,使得时间复杂度近似为O(knlnL|C|),其中k是迭代至收敛的平均迭代次数,nl是属于第l个聚类的样本个数,L是输入特征个数,|C|是聚类个数,由此可见OMVFS算法的时间复杂度也很大.DFFS-VW算法利用权重梯度选取候选模糊特征子集,减少了最优模糊特征子集的寻找范围,从而减少了算法的运行时间,时间复杂度为O(m),其中m是模糊特征个数.其中,DFFS-VW算法对SD数据集的运行时间最长,对Wine数据集的运行时间最短.从图3可以得出,原始模糊特征个数越多,算法的运行时间越长.

Fig. 3 Comparision of the running time for feature selection with different algorithms on different datasets图3 不同数据集上不同算法特征选择运行时间的比较
4.5 模糊特征变权分析

Fig. 4 The variable weight of some fuzzy features on the dataset SEA图4 数据集SEA部分模糊特征变权
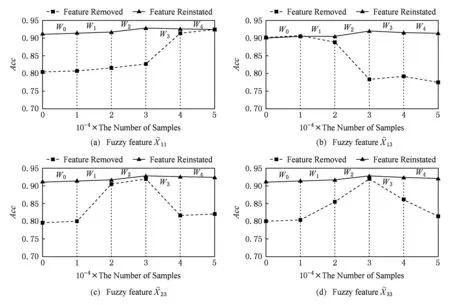
Fig. 5 The effect on classification accuracy of ignoring some fuzzy features on dataset SEA图5 数据集SEA忽略部分模糊特征前后分类准确率
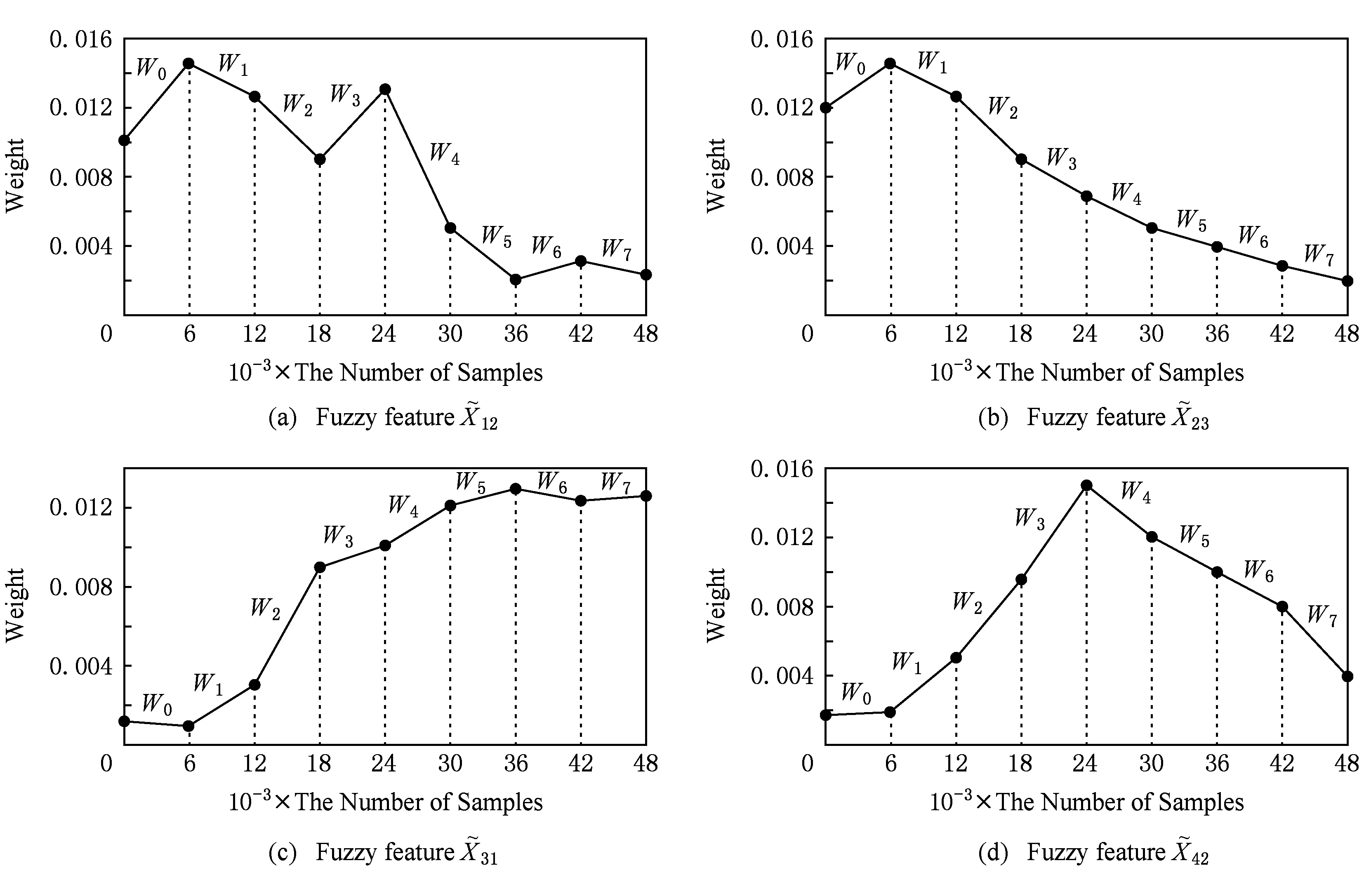
Fig. 6 The effect on predicition accuracy of ignoring some fuzzy features on dataset PPPTS图6 数据集PPPTS部分模糊特征权重的演化
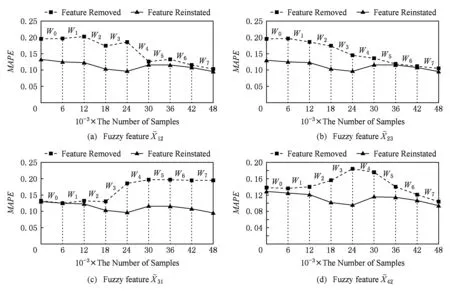
Fig. 7 The effect on predicition accuracy of ignoring some fuzzy features on dataset PPPTS图7 数据集PPPTS忽略部分模糊特征前后预测精确率对比

综上所述,DFFS-VW算法无需人为设置参数,能够自动得到最优模糊特征子集,具有良好的自适应性;利用互信息量计算特征之间的相关性,不仅考虑了特征之间的线性关系,还考虑了非线性关系,提高了特征选择结果的分类准确看和预测精确率;考虑各个模糊特征的权重,得到候选模糊特征子集,并采取后向搜索的方式得到离线模糊特征选择的优化模糊特征子集,减少了算法运行时间,提高了算法的效率;将当前窗口的候选模糊特征子集和历史模糊特征选择结果的交集作为当前窗口的初始优化模糊特征子集,根据模糊输入特征相对于初始优化模糊特征子集的重要度,获得最终的优化模糊特征子集.通过不同滑动窗口模糊特征权重的演化趋势,发现模糊输入特征对分类准确性或者预测精确性的影响.
5 总 结
本文研究动态模糊特征选择问题,无论是连续数据集,还是类别数据集,以输入特征相对与输出特征的权重作为衡量输入特征相对于输出特征之间的重要性,提出基于特征变权的动态模糊特征选择算法.在离线模糊特征选择中,首先根据特征权重,获取候选模糊特征子集.然后,结合后向特征选择方式和模糊特征筛选指标,筛选候选模糊特征子集得到优化模糊特征子集;在线模糊特征选择中,以上一个滑动窗口的优化模糊特征子集与当前滑动窗口中的候选模糊特征集的交集为基础,根据模糊输入特征在模糊特征子集中的重要度,获得当前窗口中的优化模糊特征子集.更进一步,我们分析了窗口之间模糊特征权重的变化,发现输入模糊特征的演化关系和模糊输入特征对分类准确性或者预测误差的影响.实验结果表明了本文所提动态模糊特征选择算法的有效性.但目前的滑动窗口实质上仍然是在离线采集数据的基础上反复学习获得的,本文未来将研究随着在线数据变化,自适应地确定滑动窗口大小,进一步提升动态模糊特征选择算法的性能.
[1]Xiao Jin, Xiao Yi, Huang Anqiang, et al. Feature-selection-based dynamic transfer ensemble model for customer churn prediction[J]. Knowledge and Information Systems, 2015, 43(1): 29-51
[2]Zhang Xiangrong, He Yudi, Jiao Licheng, et al. Scaling cut criterion-based discriminant analysis for supervised dimension reduction[J]. Knowledge and Information Systems, 2015, 43(3): 633-655
[3]Guyon I, Elisseeff A. An introduction to variable and feature selection[J]. Journal of Machine Learning Research, 2003, 3(3): 1157-1182
[4]Li Dan, Zhou Yuxun, Hu Guoqiang, et al. Optimal sensor configuration and feature selection for AHU fault detection and diagnosis[J]. IEEE Trans on Industrial Informatics, 2016, 13(3): 1369-1380
[5]Siwek K, Osowski S. Data mining methods for prediction of air pollution[J]. International Journal of Applied Mathematics and Computer Science, 2016, 26(2): 467-478
[6]Soguero-Ruiz C, Hindberg K, Rojo-Alvarez J, et al. Support vector feature selection for early detection of anastomosis leakage from bag-of-words in electronic health records[J]. IEEE Journal Biomedical Health Informatics, 2014, 20(5): 1404-1415
[7]Zhao Peilin, Steven C, Jin Rong. Double updating online learning[J]. Journal of Machine Learning Research, 2011, 12(may): 1587-1615
[8]Kohavi R, John G H. Wrappers for feature subset selection[J]. Artificial Intelligence, 1997, 97(1/2): 273-324
[9]Zhou Yang, Jin Rong, Steven C. Exclusive lasso for multi-task feature selection[J]. Journal of Machine Learning Research, 2010, 9: 988-995
[10]Wang Jialei, Zhao Peilin, Steven C, et al. Online Feature selection and its applications[J]. IEEE Trans on Knowledge & Data Engineering, 2006, 26(3): 698-710
[11]Li Yang, Gu Xueping. Feature selection for transient stability assessment based on improved maximal relevance and minimal redundancy criterion[J]. Proceedings of the Chinese Society of Electrical Engineering, 2013, 33(34): 179-186 (in Chinese)
(李扬, 顾雪平. 基于改进最大相关最小冗余判据的暂态稳定评估特征选择[J]. 中国电机工程学报, 2013, 33(34): 179-186)
[12]Naqvi S S, Browne W N, Hollitt C. Feature quality-based dynamic feature selection for improving salient object detection[J]. IEEE Trans on Image Processing, 2016, 25(9): 4298-4313
[13]Zhao Wei, Wang Yafei, Li Dan. A dynamic feature selection method based on combination of GA with K-means[C] //Proc of the Int Conf on Industrial Mechatronics and Automation. Piscataway, NJ: IEEE, 2010: 271-274
[14]Raza M S, Qamar U. An incremental dependency calculation technique for feature selection using rough sets[J]. Information Sciences, 2016, 343(12): 41-65
[15]Bilal I S, Keshav P D, Alamgir M H, et al. Diversification of fuzzy association rules to improve prediction accuracy[C] //Proc of the Int Conf on Fuzzy System. Piscataway, NJ: IEEE, 2010: 1-8
[16]Jing Yuege, Li Tianrui, Luo Chuan, et al. An incremental approach for attribute reduction based on knowledge granularity[J]. Knowledge-Based Systems, 2016, 104(7): 24-38
[17]Shao Weixiang, He Lifang, Lu Chunta, et al. Online unsupervised multi-view feature selection[C] //Proc of the 16th Int Conf on Data Mining. Piscataway, NJ: IEEE, 2016: 1203-1208
[18]Huang H, Yoo S, Kasiviswanathan S P. Unsupervised feature selection on data streams[C] //Proc of the 24th ACM Int Conf on Information and Knowledge Management.newyork. New York, ACM, 2015: 1031-104
[19]Li Yun, Wu Zhongfu. Fuzzy feature selection based on min-max learning rule and extension matrix[J]. Pattern Recognition, 2008, 41(1): 217-226
[20]Lughofer E. On-line incremental feature weighting in evolving fuzzy classifiers[J]. Fuzzy Sets & Systems, 2011, 163(1): 1-23
[21]Du Lei, Song Qinbao, Jia Xiaolin. Detecting concept drift: An information entropy based method using an adaptive sliding window[J]. Intelligent Data Analysis, 2014, 18(3): 337-364
[22]Wang Ling, Meng Jianyao. The dynamic clustering algorithm of Bayesian adaptive resonance theory based on local distribution[J]. Control and Decision, 2018, 33(3): 471-478 (in Chinese)
(王玲, 孟建瑶. 基于局部分布的贝叶斯自适应共振理论增量聚类算法[J]. 控制与决策, 2018, 33(3): 471-478)
[23]Comas D S, Meschino G J, Nowe A, et al. Discovering knowledge from data clustering using automatically-defined interval type-2 fuzzy predicates[J]. Expert Systems with Applications, 2016, 68(2): 136-150
[24]Ghazikhani A, Monsefi R, Yazdi H S. Online neural network model for non-stationary and imbalanced data stream classification[J]. International Journal of Machine Learning and Cybernetics, 2014, 5(1): 51-62
[25]Li Wermin, Han Jiawei, Pei Jian. CMAR: Accurate and efficient classification based on multiple class-association Rules[C] //Proc of 2001 IEEE Int Conf on Data Mining (ICDM). Piscataway, NJ: IEEE, 2001: 369-376
[26]Mu Yashuang, Liu Xiaodong, Yang Zhihao, et al. A parallel C4.5 decision tree algorithm based on MapReduce[J]. Concurrency and Computation, 2017, 29(6): 1-12
[27]Cui Yongfeng, Ma Xiangqian Li, Liu Zhijie. Application of improved BP neural network with correlation rules in network intrusion detection[J]. International Journal of Security and Its Applications, 2016, 10(4): 423-430
[28]Wang Lihuan, Guo Yonglong, Xin G. An asymmetric weighted SVR for construction final accounting prediction[J]. Journal of Information and Computional Science, 2014, 11(5): 1387-1394

