BTI作用下三因素对集成电路软差错率的影响
王 真 江建慧 陈乃金 卢光明 张 颖
1(上海电力学院计算机科学与技术学院 上海 200090) 2(同济大学软件学院 上海 201804) 3 (安徽工程大学计算机与信息学院 安徽芜湖 241000) (wangzhenqq@hotmail.com)
随着工艺尺寸的缩减,集成电路(integrated circuit, IC)的功能和性能在不断提升,但同时IC的供电电压在减小,噪声容限在降低,导致软差错率(soft error rate, SER)明显上升[1].粒子撞击如果发生在时序单元,则导致单事件翻转(single event upset, SEU),错误值被锁存;若撞击在组合逻辑电路,则导致单事件瞬态(single event transient, SET),故障脉冲只有传播到时序单元才有可能发生错误.目前面向时序电路和组合电路的SER研究已经相对成熟[2-4].其中文献[4]提出的BFIT方法更为全面和准确,通过注入故障模拟了在单个逻辑门或锁存器发生SET,融合了对逻辑屏蔽、电气屏蔽以及锁存窗屏蔽的考虑,求出整个电路的SER.
尽管许多考虑工艺缩减的SER分析工作已经达到较高的准确性,但对老化效应如何影响SER的研究尚不全面.老化效应缩短器件寿命,降低器件性能,给电路带来损耗,尤其是偏置温度不稳定性(bias temperature instability, BTI),包括发生在PMOS中的负偏置温度不稳定性(negative bias temperature instability, NBTI)和发生在NMOS中的正偏置温度不稳定性(positive bias temperature instability, PBTI),已经成为现代IC可靠性分析的主要因素[5-6].有实验数据表明,电路中的门节点经受10年NBTI效应作用,最坏情况表现为其内部的PMOS晶体管的阈值电压绝对值约有50 mV的上升,约20%的电路时延增加[7],近20%的电路SER提升[8],导致电路更容易出现功能失效.由此看来,研究BTI对SER的影响是十分必要的.
目前,BTI效应对SER的影响还未被充分研究.文献[9]开始探索老化因素(包括热载流子现象和NBTI)对组合电路SER的影响,但对NBTI如何影响关键电荷值(记作Qcrit)并未展开讨论;文献[10-11]描述了老化机制下Qcrit的变化,却只聚焦于SRAM设计;文献[8]对NBTI如何影响晶体管Qcrit的原理进行了初步介绍并结合到SER中;文献[12]开始面向BTI效应较为深入地研究了Qcrit的变化及其对SER的影响,其中由仿真实验得到1组基本门在应力时间0~10年的Qcrit值,归纳出Qcrit变化解析模型并加以验证;而从SET脉宽的角度,文献[13]曾聚焦于NBTI研究了SMIC130 nm工艺下SET脉冲宽度的变化,但未将其考虑到SER的评估中;文献[14]设计了脉宽测量电路,仅以测量结果解释了NBTI下SET脉宽展宽现象;从延迟的角度,文献[15]也仅面向NBTI分析了延迟的变化.已有的工作多数集中在对NBTI的分析,是因为一般情况下NBTI比PBTI对电路造成的损害更显著,然而,有研究表明:从延迟的角度分析,输入占空比越高,NBTI影响越小,PBTI影响越大,因此PBTI也不容忽视[16].另外,现有工作都从BTI影响的单个因素着手,而考虑BTI导致的多个因素变化对SER产生的影响,据我们所知,目前国际上还未见相关研究.
为了全面而准确地分析BTI对SER的影响,本文工作分为2部分:1)研究了BTI导致的多个因素的变化,包括关键电荷值、SET故障脉冲宽度和门延迟;2)分析这3个因素的变化对SER的影响.由此,本文的创新点包括2个方面:
1) 在BTI作用下门延迟对SER的影响研究工作的基础上[17],进一步研究了SET故障脉冲宽度和关键电荷值对SER的影响.结果表明,SER随着应力时间的延长而增大,其中关键电荷值的影响最为显著,延迟和SET脉宽影响较小.
2) 在研究BTI作用下关键电荷值、SET故障脉冲宽度和门延迟3个因素的变化以及它们对SER的影响中,通过考虑PBTI,补充了BTI作用下基于32 nm工艺SET脉宽变化模型的设计,并对模型加以验证;在分析SET脉宽变化对SER的影响时,提出了将SET脉宽变化映射到注入电荷量变化的解析模型.
本文的工作可以为后续研究提供参考,同时帮助设计人员选择软差错率增长较高的电路主要针对关键电荷因素来考虑加固方案.
1 背景介绍
1.1 BTI效应及其影响
BTI效应导致Si与SiO2界面处生成电荷,产生陷阱,因而阻碍了施加在栅极的电压应力,导致了阈值电压的升高.把阈值电压的增量记作ΔVth,可以表示为[16]
ΔVth=qδ(1+m)CoxNIT(t),
(1)
这里,q,m,Cox分别表示电子电荷数、载流子迁移率减少量和氧化物电容;δ为BTI系数,NMOS管的δ=0.5,PMOS管的δ=1;而NIT(t)表示界面陷阱的数目,由RD(reaction diffusion)模型[18]知:
NIT(t)=(kfN0kr)(kH
(2)
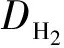
MOS管的漏端饱和电流可以近似表示为[15]

(3)
本文中Vg和Vth表示栅源压差绝对值和阈值电压绝对值,以便对PMOS和NMOS统一推导;μ为载流子迁移率;W和L分别为晶体管的宽度和沟道长度.从而,Vth的变化必定带来Id的变化,而由于MOS管延迟可以表示为Id的函数[19],我们推导出BTI应力下MOS管延迟增量ΔTd满足[17]:

(4)
其中,Vth0是MOS管在BTI应力之前的阈值电压绝对值,Td0是受BTI应力之前MOS管的传输延迟.
另外,文献[12]分析出BTI影响下MOS管关键电荷值会减小,其基于BTI对晶体管阈值电压及漏端饱和电流的影响,通过HSPICE模拟得出了基本逻辑门(包括非门和2输入、3输入、4输入的与/或非门)经历BTI效应0~10年时的关键电荷值Qcrit.随着经历BTI效应时长的变化,关键电荷值可以表示为时长的解析模型,因而在不同工艺和电气参数下Qcrit的变化值也可以得出.由于本文仅使用Qcrit的具体值,所以对解析模型不再赘述.
1.2 BFIT方法及延迟在SER中的考虑
在评估SER的方法中,小规模电路可以通过故障注入.如果以注入电流方式模拟软故障,通常选用双指数电流模型[20]:
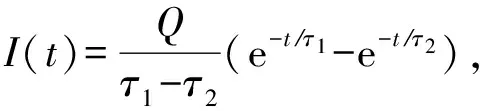
(5)
其中,Q是撞击节点收集的电荷量,τ1是收集时间常数,τ2代表离子轨迹建立时间常数.
BFIT方法以FIT(failure-in-time)作为度量指标,即109h内发生失效的次数,能够较为准确和全面地评估大规模时序电路的SER[4],即:
FIT=avg(failures/cycle)×cycles/109,
(6)
其中,每周期内的失效数由粒子撞击节点产生软故障的概率以及软故障传播到锁存器并被锁存的概率来决定,因此单位周期内的失效率记为[21]
failures
(7)
其中,R(Q,t)表示电量为Q的粒子在时刻t撞击到门节点的概率;N(Q,t)是一个布尔值函数,当撞击导致电路最终输出错误时其值为1,否则为0,其作用为在实际操作中找出那些没有被逻辑屏蔽、电气屏蔽和锁存窗屏蔽的导致单个或多个锁存器捕获故障脉冲的(Q,t).
BFIT对软故障的模拟是通过在时钟周期的不同时刻注入不同电荷量来完成的.BFIT实现过程中,首先列出被测电路涉及到的各种基本逻辑门的延迟信息、在不同时刻注入的电荷量,以及对应不同注入电荷量的MOS管差错率;然后,由锁存器向原始输入端回溯找到敏化路径,从而考虑了逻辑屏蔽,建立路径的同时计算每个门节点到目标锁存器的延迟,根据此延迟在先前列出的信息中找到该时刻注入的电荷量,继而取出注入该电荷量的差错率,其间考虑了电气屏蔽和锁存窗屏蔽;最后,由敏化路径上每个门节点的软差错概率求和来完成积分运算.
基于BFIT方法,我们分析了如何在SER的计算中考虑延迟的变化[17].依据MOS管受BTI影响延迟变化的解析式(4),将延迟变化信息结合到对SER电气屏蔽的分析中.
2 BTI对SET脉宽的影响
电路中的MOS晶体管经受BTI效应后,阈值电压升高,从而导致延迟、关键电荷值和SET故障脉冲都会发生变化.本节主要通过仿真实验、理论推导,建立了SET脉宽变化模型.
我们基于PTM32nm工艺[22]对NBTI和PBTI影响下SET脉冲宽度的变化进行全面分析.首先借助实验建立SET脉冲宽度与入射粒子沉积电荷量(Q)和MOS管漏端饱和电流(Id)的关系,这不仅是发现BTI对SET脉宽如何影响的基础,也对指导抗SET加固设计具有重要意义.之后由于BTI会导致MOS管Vth,Id等电气参数随时间退化,进而推出SET脉宽随时间变化的解析模型.
2.1 SET脉宽与积聚电荷量和漏端饱和电流的关系
我们分别面向PBTI和NBTI开展了类似的实验过程:在HSPICE模拟中选取双指数电流源(见式(5))注入故障,其中对参数τ1,τ2的取值与文献[12]保持一致,固定Id注入不同的电量Q记录对应的SET脉宽(TSET)值,从而可以得出TSET随Q的变化规律;固定Q改变Id记录随之而变的TSET,从而可以分析出TSET随Id的变化规律;最后归纳出TSET与Q和Id的关系.接下来,我们以PBTI为例进行具体说明.
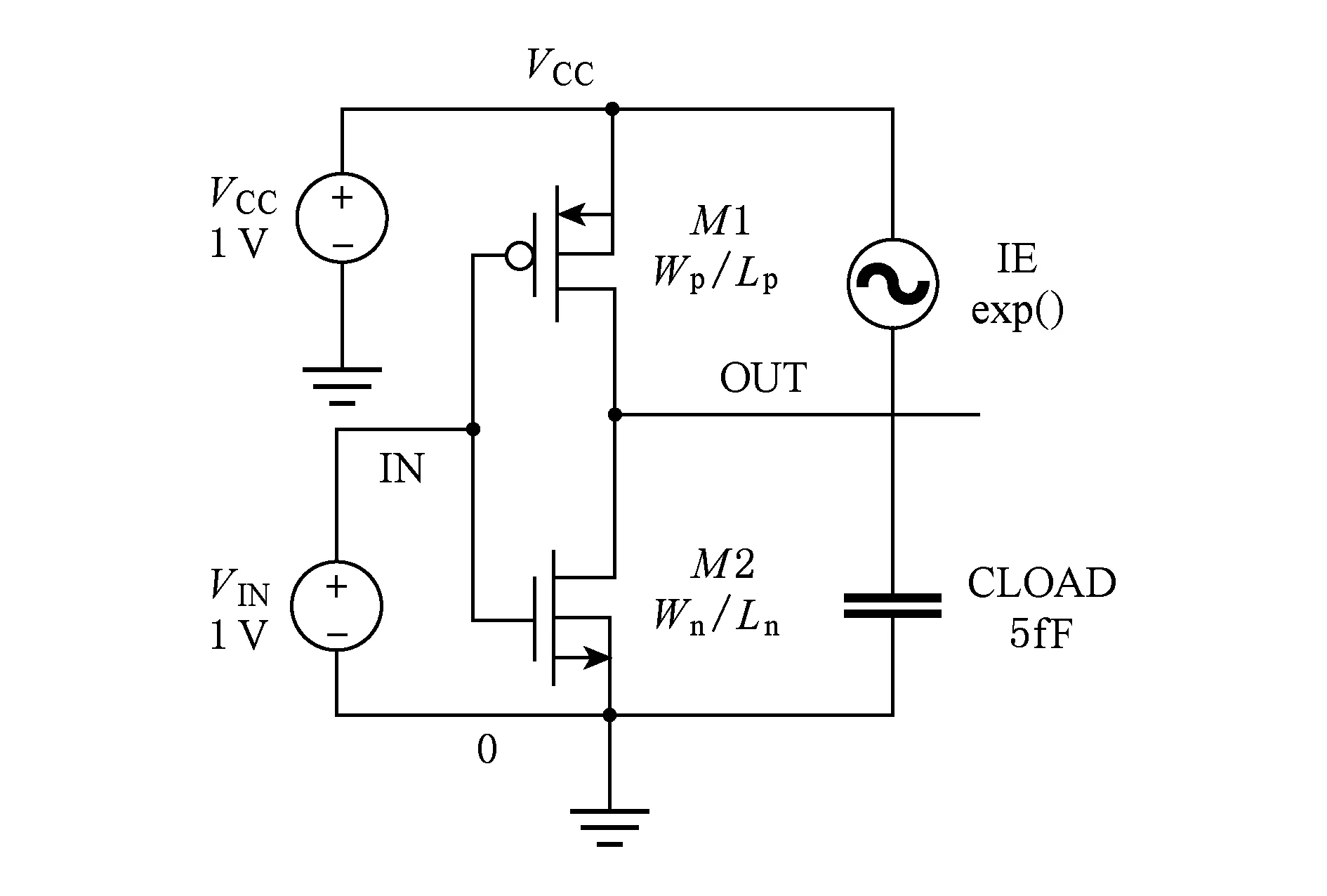
Fig. 1 The simulated circuit structure图1 模拟电路结构
模拟电路为1个反相器,如图1所示,由于PBTI的应力阶段在NMOS的导通状态,使反相器输入保持在高电平(VIN=1V),为了模拟SET故障,在PMOS管M1的2端加上电流源IE,输出端接5fF的理想电容CLOAD以便观察输出波形.对电流源模型式(5)中的注入电荷量选取了远大于Qcrit的1组值80~160fC,对输出端的故障脉冲记录半峰值脉宽.如表1所示,为了便于总结规律,我们通过将NMOS管宽度(Wn)从48 nm增加到128 nm来获取6组实验数据,每组含5对(Qcrit,TSET)值,其中PMOS管宽度(Wp)保持为64 nm,NMOS管的长度(Ln)和PMOS管的长度(Lp)均保持为32 nm.
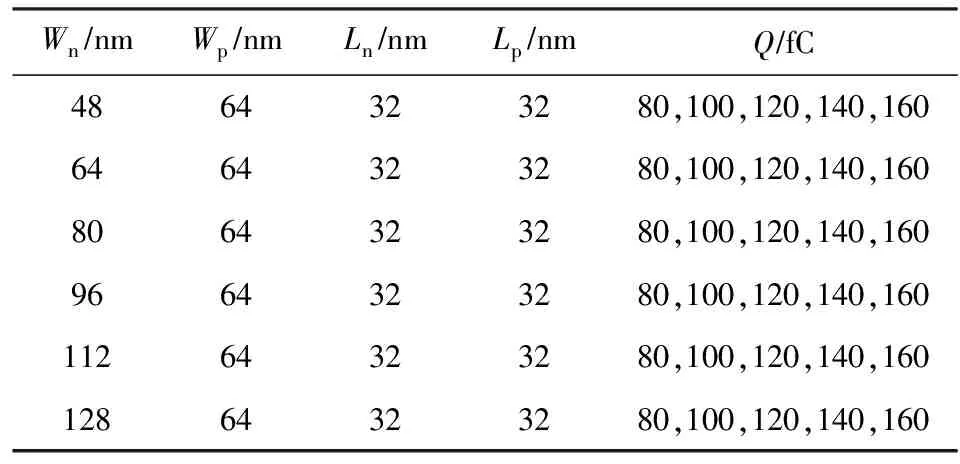
Table 1 The Device Width, Length and the Injected Charge Value
由于每一组实验数据(即表1中的每一行)中NMOS管宽度Wn固定,根据式(3)可知NMOS的漏端饱和电流(Idsn)就固定,这样可以模拟使用同样NMOS管时,不同入射粒子沉积电荷量导致的软故障脉冲.通过6组实验,图2给出了TSET与粒子积聚电荷Q在不同NMOS管下的关系,图2中每一种形状的点表示HSPICE中输入与输出数据,点上的直线为MATLAB拟合所得,观察可知,在相同Wn下,TSET随Q线性增加,即得在相同Idsn下,TSET正比于Q.
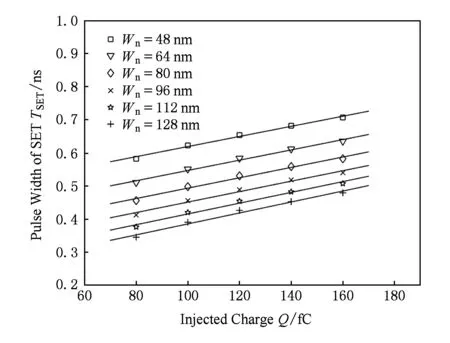
Fig. 2 The relation of TSET and Q under different Wn图2 TSET与Q值在不同Wn下的关系
类似地,当需要建立TSET与Idsn的关系时,我们运用表1中的数据,但这次每一组实验固定Q、改变Wn,相当于改变Idsn,观测对应的软故障脉冲宽度,然后变换Q得到5组实验数据.图3给出了TSET与Idsn在不同Q下的关系,运用双对数坐标,曲线呈递减趋势且基本平行,因此,在相同Q下,TSET正比于(Idsn)-α.基于本文所用工艺库,我们测得α的均值为0.4.
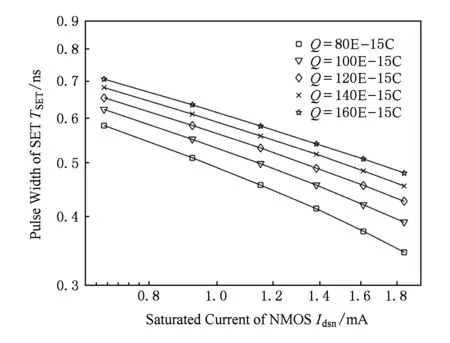
Fig. 3 The relation of TSET and Idsn under different Q图3 TSET与Idsn在不同Q下的关系
综合上述结果,我们可以推出在NMOS导通时,成立关系:
TSET∝Q×(Idsn)-α.
(8)
另外,考虑NBTI效应,即在PMOS导通状态,我们进行了类似的实验,记录实验数据,并分析得出TSET与Q和PMOS管的漏端饱和电流(Idsp)具有与式(8)相似的关系:
TSET∝Q×(Idsp)-α,
(9)
同时测得α的均值为0.34.
把式(8)和式(9)统一起来可得:
TSET∝Q×(Id)-α,
(10)
其中Id即MOS管漏端饱和电流,与式(3)标识一致.
2.2 BTI导致的SET脉宽变化
对式(3)的两边求导,并同时除以式(3)的两边可得:

(11)
对式(10)进行同样运算可得:

(12)
将式(11)代入式(12)可得:

(13)
对式(13)的两边积分得:
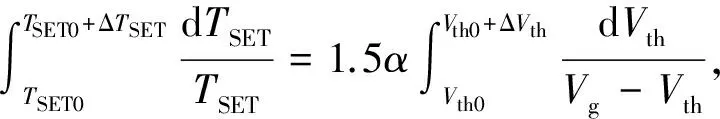
(14)
其中,TSET0表示经历BTI效应之前粒子撞击晶体管产生的SET脉冲宽度,ΔTSET为经历BTI时长t之后的脉宽增量.对式(14)计算得出:
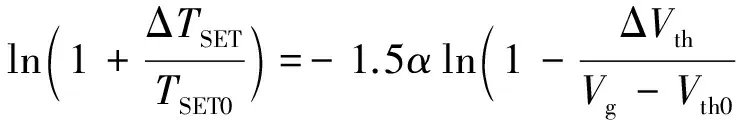
(15)
对式(15)的两边进行泰勒展开,省略高阶项则有:
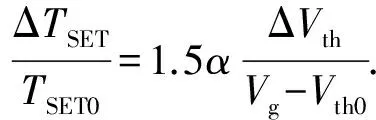
(16)
将式(1)代入式(16)可推出:

(17)
由式(17)可知ΔTSET为时间t的函数.
3 BTI在SER评估中的考虑
基于BFIT方法,在将BTI作用下的延迟考虑到SER计算的基础上[17],本节结合了关键电荷、SET脉宽等因素,从而在SER评估中全面考虑BTI的影响.
3.1 关键电荷值的变化在SER中的考虑
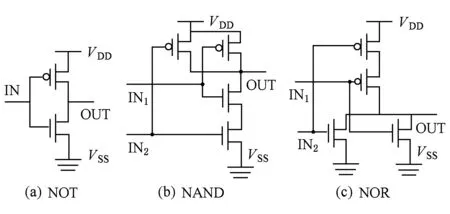
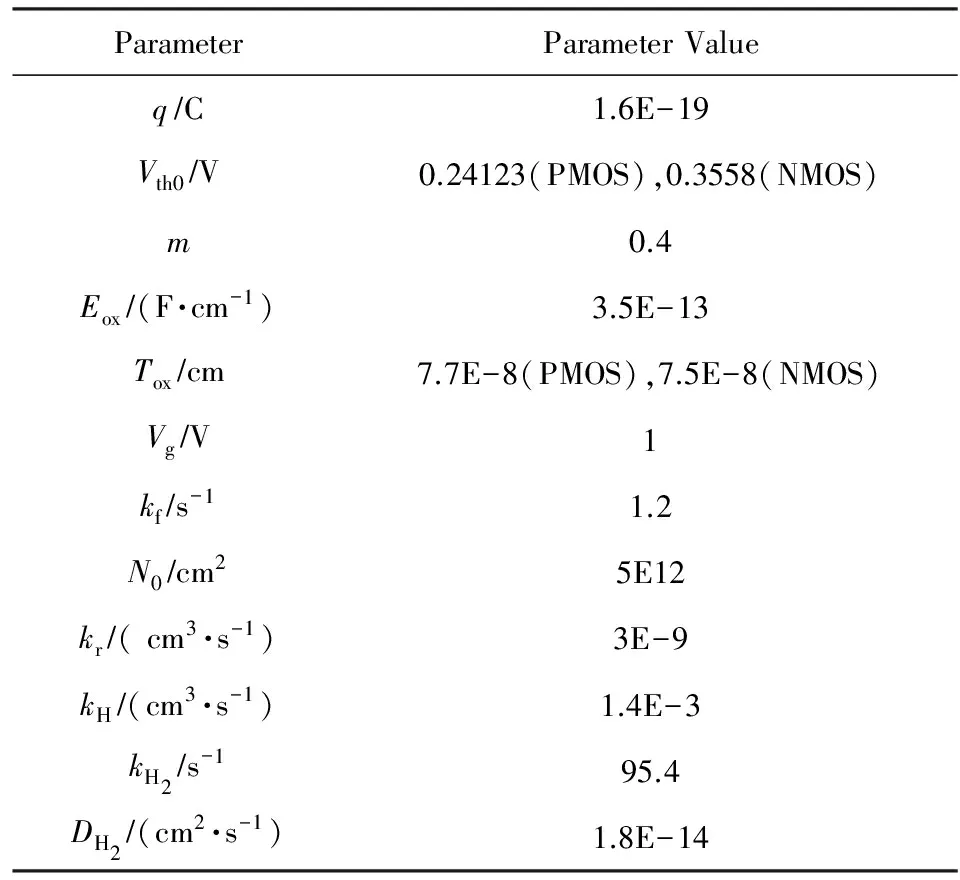
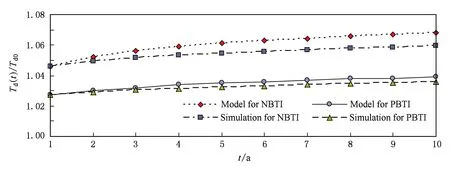
在SER的计算中,只有注入电荷量大于关键电荷值才有可能发生软差错,因此,当Q (18) 每秒钟电荷量超过Q的撞击数表示为[17] R(Q)=F×A×K×e-QQS, (19) 其中,F表示粒子流量,A表示收集电荷的门节点处敏感漏端面积,K是与工艺无关的拟合参数,而QS表示电荷收集率,是与工艺相关的拟合参数且NMOS的电荷收集率往往大于PMOS.假设粒子撞击概率随时间均匀分布,则R(Q,t)可以通过dR(Q)dQ来计算. 由1.2节可知,N(Q,t)不是解析式,而是用于标识仅有部分(Q,t)参与计算,例如对逻辑屏蔽而言,沿敏化路径传播的SET使得N(Q,t)=1,而在敏化路径之外的,则使得N(Q,t)=0,此时式(18)也就无需计算.那么针对N(Q,t)=1的情况,代入R(Q,t)与式(19)的关系式,从程序实现的角度,式(18)可以表示为 (20) 其中,tstep是分割的时间步长,Q是注入电荷的离散值,范围从Qcrit到设定的电荷量上限Qmax.由1.1节可知BTI效应会影响Qcrit值,在最终的计算中,将经历不同操作时长后各个基本门受PBTI和NBTI影响后的Qcrit代入式(20),可以从关键电荷的角度将BTI影响结合到SER的计算中. 将Qcrit值代入式(20)的过程本文进行了如下设计.由1.1节可知,对非门,2输入、3输入、4输入的与或非门受PBTI和NBTI影响0年、1年、5年、10年后的Qcrit已得出,因而将在PMOS导通时代入受NBTI影响的Qcrit值,而在NMOS导通状态代入受PBTI影响的Qcrit.根据非门、与非门和或非门的电路图,可以得知各种基本门输出为信号0时,都为NMOS管的导通状态,而输出为信号1时,则为PMOS管的导通状态.图4中给出了2输入的与非门(NAND)和或非门(NOR),更多输入的逻辑门电路图与之类似.由此可以将PBTI和NBTI对Qcrit的影响都考虑到SER的分析中. Fig. 4 The circuit diagram of NOT,NAND and NOR图4 非门、与非门和或非门的电路图 粒子撞击电路节点时产生的SET脉冲宽度随着经历BTI时间的延长而增大,在BFIT对SER的计算中我们将这种故障脉冲宽度的增大映射为注入电荷量Q的增多,假设BTI作用时长t后,注入Q(t)的电荷量可以模拟SET脉宽的变化,这样可把式(10)记为 TSET(t)=A×Q(t)×(Id(t))-α, (21) 其中,A代表一个正比例系数;TSET(t),Q(t),Id(t)分别表示BTI作用时长t后的SET脉宽、模拟注入电荷量及漏端饱和电流. 根据式(3),我们可将Id(t)表示为 (22) 其中,B指代系数,Vth0表示未经历BTI效应时的阈值电压,其他参数与本文前述保持一致.将式(1)代入式(22),再将变换后的式(22)代入式(21)可得: TSET(t)=AB-αQ(t)(Vg-Vth0-Ct1/6)-1.5α, (23) 由式(17)结合t=0时的式(23)可得: (24) 这样,结合式(23)(24),运算可得: (25) 其中,系数C与式(23)中保持一致. 由式(25)可以看出,在模拟SET注入电荷量Q(t)的解析模型中,只有t是变量,给t赋值0年、1年、5年和10年,即与结合关键电荷值变化的时长一致,则Q(t)可以在原来注入的电荷量Q0的基础上乘以不同系数获得.从而,对应不同时长t,通过变换注入电荷量,把BTI作用不同时长t后SET脉冲宽度的变化结合到SER的计算中,其中对PBTI和NBTI的考虑与3.1节分析类似. 本文使用32 nm HKMG(high-kmetal-gate) PTM 工艺库[22],实验环境为Windows10 x64 OS,8 GB内存,Intel®CoreTMi7-6500U 2.5 GHz处理器.对BTI作用下延迟和SET脉宽的变化模型,通过HSPICE仿真进行了实验验证,同时使用C++实现模型分析了这2个因素对SER的影响.为进一步观察各因素影响下的SER,基于ISCAS89基准电路得出了BTI作用不同时长后SER的变化. 从第2节可知,延迟和SET脉宽的变化模型分别由式(4)和式(17)获得.2个模型中所用参数如表2所示,其中,Vth0和氧化物厚度Tox查自PTM工艺库,q和氧化物介电常数Eox源于文献[19],其余参数与文献[12,23-24]一致.需要指出的是,氧化物电容Cox=Eox÷Tox[19].在经历BTI效应时长t后,得到延迟和SET脉宽与其未受BTI影响时的比例.另外,使用HSPICE提供的MOSRA API模拟0~10年的BTI应力,基于PTM工艺库以及相匹配的MOSRA模型库,以反相器为例测量了NBTI下PMOS延迟变化和PBTI下NMOS延迟变化,在此基础上,注入双指数电流模型模拟软故障,观测输出端SET脉宽.图5和图6显示了分别由解析模型和HSPICE仿真得到的数据,图5为延迟比例与应力时长的关系,图6为SET脉宽比例与应力时长的关系.我们分别对图5和图6中对应相同横坐标的Model for P/NBTI数据和Simulation for P/NBTI数据计算距离均值来衡量误差,发现延迟和SET脉宽变化模型的误差均小于0.5%,可见,解析模型得到的变化比例与仿真实验数值相近,趋势一致. Table 2 Parameters in the Models of Delay Variation and SET Pulse Width Variation Fig. 5 The delay variation ratio by HSPICE simulation and by the proposed model图5 由HSPICE仿真和解析模型得到的延迟变化比例 Fig. 6 The variation ratio of SET pulse width by HSPICE simulation and by the proposed model图6 HSPICE仿真和解析模型得到SET脉宽变化 由图5和图6可以发现,两者受NBTI的影响都高于PBTI,例如在3年时,延迟受NBTI影响增加5.6%,受PBTI影响增加3.2%.且在1~10年的时间里,前期BTI影响相对较大,随着时间的延长而趋于缓和.而从图5和图6中纵轴数值看,无论是延迟Td(t)还是SET脉宽TSET(t),变化比例都非常接近1,因此说明在本文所用工艺和现有参数下,受BTI影响的延迟和SET脉宽这2个因素对SER的影响微乎其微. 我们在BFIT程序中综合考虑了关键电荷、SET脉冲宽度和延迟的变化,其中对输入电路的处理和式(20)参数的取值与文献[17]一致,对关键电荷、SET脉冲宽度的结合依据本文第3节,考虑到记录最终结果的精度需求和内存开销,程序中对SER值选取单精度浮点型,在此条件下所得到的实验数据与结合两因素的结果(见文献[17])相比未显示变化,本节不再列出. 实验表明,BTI效应下晶体管相关参数的变化,主要为关键电荷因素的变化,对于SER评估的影响不容忽视.同时,随着经受BTI影响的时间的延长,电路SER持续增大,初期会增长较快,后面数年增长趋势减缓. 需要说明的是,由于相关工作中主要考虑NBTI的影响[13,15]且未结合到完整的SER评估中去[12],目前无法进行对比实验.另外,本文基于的工艺库取自NIMO(nanoscale integration and modeling)组的工作结果[22],因他们没有提供相匹配的包含电气信息的SPICE电路网表,因此对该部分实验未能进行仿真验证. 本文在BTI作用下门延迟对SER的影响研究工作的基础上,进一步研究了SET故障脉冲宽度和关键电荷值对SER的影响,从而将3个因素融合到SER的计算中.由MOS管延迟受BTI作用的变化模型发现,延迟增加量与未经历BTI应力时的延迟相关,相关系数与应力时间呈幂函数关系,时间指数为1/6,且延迟受NBTI影响变化大约是PBTI的2倍.本文基于HSPICE进行电路模拟,建立了32 nm工艺下SET脉冲宽度受BTI作用后的解析模型,脉宽增量的模型与延迟类似,应力时间相同时,脉宽增大比例为一定倍数的延迟增加比例(此倍数在本文实验参数下,NBTI对应0.34,PBTI对应0.4).在将3个因素结合到BFIT方法的过程中,本文进一步分析出SET脉宽的变化可以体现在模拟注入电荷量的变化上.由最终的实验数据可以发现,在现有资料获取参数和本文所用工艺下,BTI导致的延迟变化和SET脉宽变化对SER的影响微乎其微,而BTI导致关键电荷值的变化会对SER产生不容忽视的影响,BTI效应随着时间的增长导致SER增大比例会变大,但最初的一年影响最大,之后影响变缓.期望我们的工作对电路的选择性加固设计提供依据,有效指导集成电路的容错设计. [1]Liu Baojun, Cai Li, Liu Xiaoqiang, et al. Research advance in reliability for nano-meter CMOS circuits under single event effects[J]. Micronanoelectronic Technology, 2016, 53(1): 1-6 (in Chinese) (刘保军, 蔡理, 刘小强, 等. 纳米CMOS电路在单粒子效应下可靠性研究进展[J]. 微纳电子技术, 2016, 53(1): 1-6) [2]Uemura T, Lee S, Pae S, et al. Investigation of logic circuit soft error rate (SER) in 14 nm FinFET technology[C] //Proc of IEEE Int Reliability Physics Symp. Piscataway, NJ: IEEE, 2016: 3B-4-1-3B-4-4 [3]Li Ji, Draper J. Joint soft-error-rate (SER) estimation for combinational logic and sequential elements[C] //Proc of the 15th IEEE Computer Society Annual Symp on VLSI. Piscataway, NJ: IEEE, 2016: 737-742 [4]Holcomb D, Li Wenchao, Seshia S A. Design as you see FIT: System-level soft error analysis of sequential circuits[C] //Proc of the 16th Conf on Design, Automation and Test in Europe. New York: ACM, 2009: 785-790 [5]Keane J, Kim T H, Kim C H. An on-chip NBTI sensor for measuring PMOS threshold voltage degradation[C] //Proc of IEEE Int Symp on Low Power Electronics and Design. Piscataway, NJ: IEEE, 2007: 189-194 [6]Huard V, Denais M. Hole trapping effect on methodology for DC and AC negative bias temperature instability measurements in PMOS transistors[C] //Proc of the 42nd IEEE Int Reliability Physics Symp. Piscataway, NJ: IEEE, 2004: 40-45 [7]Jin Song. Analysis, forecasting and optimization technology research for aging effects of CMOS integrated circuit [D]. Beijing: University of the Chinese Academy of Sciences, 2011 (in Chinese) (靳松. CMOS集成电路老化效应的分析、预测及优化[D]. 北京: 中国科学院大学, 2011) [8]Lin C Y H, Huang R H M, Wen C H P, et al. Aging-aware statistical soft-error-rate analysis for nano-scaled CMOS designs[C] //Proc of the 9th Int Symp on VLSI Design, Automation and Test. Piscataway, NJ: IEEE, 2013: 1-4 [9]Ramakrishnan K, Rajaraman R, Suresh S, et al. Variation impact on SER of combinational circuits[C] //Proc of the 8th Int Symp on Quality Electronic Design (ISQED). New York: ACM, 2007: 911-916 [10]Bagatin M, Gerardin S, Paccagnella A, et al. Impact of NBTI aging on the single-event upset of SRAM cells[J]. IEEE Trans on Nuclear Science, 2010, 57(6): 3245-3250 [11]Cannon E H, Osowski A K, Kanj R, et al. The impact of aging effects and manufacturing variation on SRAM soft error rate[J]. IEEE Trans on Device & Materials Reliability, 2008, 8(1): 145-152 [12]Rossi D, Omana M, Metra C, et al. Impact of bias temperature instability on soft error susceptibility[J]. IEEE Trans on VLSI Systems, 2015, 23(4): 743-751 [13]Chen Jianjun, Chen Shuming, Liang Bin, et al. NBTI induced SET pulse broadening in the production and propagation[J]. Acta Electronica Sinica, 2011, 39(5): 996-1001 (in Chinese) (陈建军, 陈书明, 梁斌, 等. NBTI效应导致SET脉冲在产生和传播过程中的展宽[J]. 电子学报, 2011, 39(5): 996-1001) [14]Harada R, Mitsuyama Y, Hashimoto M, et al. Impact of NBTI-induced pulse-width modulation on SET pulse-width measurement[J]. IEEE Trans on Nuclear Science. 2013, 60(4): 2630-2634 [15]Paul B C, Kang K, Kufluoglu H, et al. Negative bias temperature instability: Estimation and design for improved reliability of nanoscale circuits[J]. IEEE Trans on Computer-Aided Design of Integrated Circuits and Systems, 2007, 26(4): 743-751 [16]Khan S, Hamidioui S, Kukner H, et al. BTI impact on logical gates in nano-scale CMOS technology[C] //Proc of the 15th IEEE Int Symp on Design & Diagnostics of Electronic Circuits & Systems. Piscataway, NJ: IEEE, 2012: 348-353 [17]Wang Zhen, Jiang Jianhui, Chen Naijin. Bias temperature instability-aware soft error rate analysis[J]. Journal of Electronics and Information Technology, 2017, 39(7): 1640-1645 (in Chinese) (王真, 江建慧, 陈乃金. 考虑偏置温度不稳定性的软差错率分析[J]. 电子与信息学报, 2017, 39(7): 1640-1645) [18]Alam M A, Mahapatra S. A comprehensive model of PMOS NBTI degradation[J]. Microelectronics Reliability, 2005, 45(1): 71-81 [19]Rabaey J M. Digital Integrated Circuits—A Design Perspective[M]. Beijing: Tsinghua University Press, 1998: 133-134 [20]Messenger G C. Collection of charge on junction nodes from ion tracks[J]. IEEE Trans on Nuclear Science, 1982, 29(6): 2024-2031 [21]Holcomb D, Li Wenchao, Seshia S A. BFIT users guide-v1.1[CP/OL]. 2009 [2016-11-01]. http://www.eecs.berkeley.edu/?holcomb/BFIT.htm [22]Nanoscale Integration and Modeling (NIMO) Group. Predictive Technology Model-Latest Models: 32 nm PTM model for metal gate/high-k CMOS, Version2.0[DB/OL]. 2007 [2016-11-01]. http://ptm.asu.edu/ [23]Islam A E, Kufluoglu H, Varghese D, et al. Recent issues in negative-bias temperature instability: Initial degradation, field dependence of interface trap generation, hole trapping effects, and relaxation[J]. IEEE Trans Electron Devices, 2007, 54(9): 2143-2154 [24]Krishnan A T, Reddy V, Chakravarthi S, et al. NBTI impact on transistor and circuit: Models, mechanisms and scaling effects[C] //Proc of IEEE IEDM’03. Piscataway, NJ: IEEE, 2003: 14.5.1-14.5.4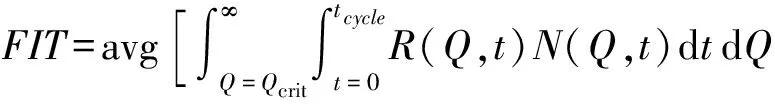

3.2 SET脉冲宽度的变化在SER中的考虑
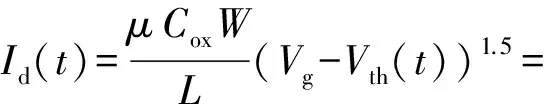



4 实验与结果分析
4.1 考虑延迟和SET脉宽变化的实验验证与分析
4.2 BTI影响下的SER
5 结 论

