不同截面形态的空心抗滑桩支挡效果对比研究

易靖松，张世林，孙金辉，鲜杰良，蔡佳君

(中国地质科学院探矿工艺研究所/中国地质调查局地质灾害防治技术中心，四川 成都 611734)

在抗滑桩的运用研究过程中，空心抗滑桩引起了越来越多的关注和研究。空心抗滑桩因其自身的结构特点，具有集抗滑桩和集水井于一体的优点，用于边坡治理不但和传统抗滑桩一样可以承受较大的横向荷载，而且由于其空心构造，可以降低滑体内地下水位，降低滑体重度，提高滑体自身的稳定性，且受力更加合理。相比于传统抗滑桩，空心截面抗滑桩更经济，特别是在桩身长，受力大，截面的钢筋和砼用量多的情况下，更能体现出它的优越性，是一种很有发展潜力的新型抗滑桩[1～6]。

空心抗滑桩的截面形式跟传统抗滑桩一样，一般有矩形或圆形，都是利用桩体自身的强度将滑体剩余下滑力传递到滑面以下稳定地层，从而保证边坡的整体稳定[7～10]。虽然空心抗滑桩具有以上诸多优点，但在实际工程案例中，却很少看到空心抗滑桩的使用，原因在于空心抗滑桩在边坡治理工程的研究历程中缺少更多的理论和优化技术来支撑。基于这种情况，本文以缓倾顺层岩质滑坡为试验模型，对矩形和圆形空心抗滑桩展开了一系列对比研究。

1 实验准备

1.1 实验总体布置

在红层的砂泥岩互层地区，时常发生较大规模的缓倾顺层基岩滑坡，造成大量的人员伤亡和财产损失，而该类滑坡的地质模型通常是坚硬的砂岩层下覆软弱的泥岩层，砂岩层形成滑体，软弱泥岩泥化后形成滑带。基于此，本项研究以缓倾顺层基岩滑坡为模型，根据试验室现有模型槽尺寸(3 m×2 m×1 m)设计制作滑体模型。实验分两组进行：一组为矩形截面集水空心抗滑桩，一组为圆形截面空心抗滑桩。

实验采用液压千斤顶设备施加荷载，空心桩位于滑体中部，采用全埋式布置，前缘为4根悬臂式实心抗滑桩。由于本文主要研究不同截面形态的空心抗滑桩支挡效果，因此，对前缘的实心抗滑桩不作对比研究。本项2组实验总体布置平面图见图1，图中未标注尺寸的均以mm为单位。

图1 不同截面空心桩实验模型图(单位：mm)Fig.1 Experimental model of hollow piles of different cross sections(mm)

1.2 抗滑桩设计

(1)尺寸设计

根据相似比理论，本次试验按圆形桩基于原型桩尺寸为外径3 m、内径2.2 m，矩形桩原型外围尺寸3 m×2 m设计，室内模型试验采用缩尺比例为1∶10的几何相似模型，拟设定坡度为10°。考虑到用相同材料比较容易满足相似条件, 采用“放松重力效应”模型，即选择以下相似比参数：

cl=1/10,cE=1,cμ=1

根据单值量判据相等，得到下列各单值量的相似常数：模型上施加的集中力为原型的1/100；模型上施加的线荷载为原型的1/10； 模型上施加的面荷载为与原型相等。具体尺寸设计方案见表1。

表1 空心抗滑桩尺寸设计方案表Table 1 Dimensional design scheme of a hollow pile

若假设原型桩间距为8 m，则对应的模型桩间距为0.8 m，共2根；根据相似比参数，选取整个模型的几何尺寸为长3.5 m、宽1.6 m、高1 m，桩间距0.8 m(图2)。

模型槽沿滑坡周边用角钢焊接，内设木板，形成框架，滑床用混凝土浇注而成，使用粉质黏土或细砂配比模拟滑面，厚度1 cm。

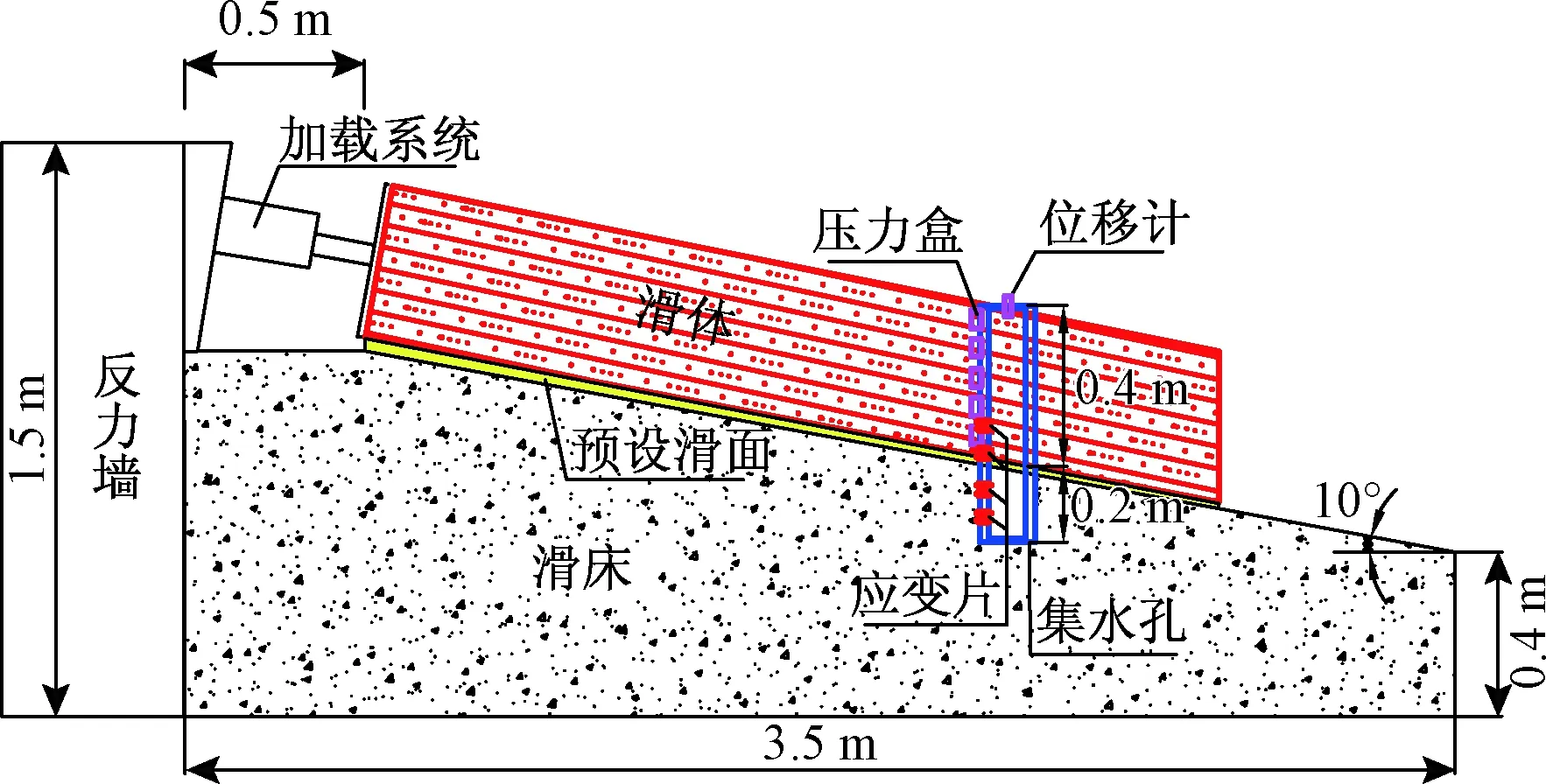
图2 试验模型剖面图Fig.2 Profile of the test model

(2)配筋设计

空心抗滑桩的截面分为矩形和圆形两种形式。矩形桩外截面尺寸为200 mm×300 mm，内截面尺寸为120 mm×220 mm；空心桩受拉一侧配筋为5Ф6，受压一侧配筋为4Ф6，箍筋采用Ф2﹫100，混凝土标号为C25，桩间距0.8 m，配筋图见图3(a)。

圆形抗滑桩外截面直径为300 mm，内截面直径为220 mm；钢筋间距60 mm，配筋为14Ф6，箍筋采用Ф2﹫100，混凝土标号为C25，桩间距0.8 m，配筋图见图3(b)。

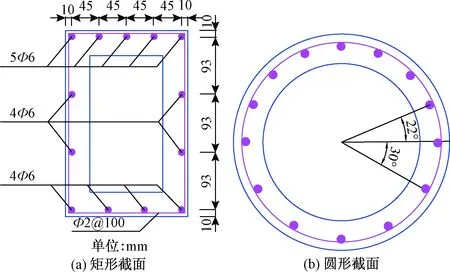
图3 不同截面空心桩配筋示意图Fig.3 Reinforcement for hollow piles of different cross sections

(3)测点布置设计

①应变数据测点：在抗滑桩的纵向受力钢筋表面每隔10 cm设置应变片。应变片采用粘贴的方式布设在钢筋表面，用于测量钢筋的应变，并用来计算抗滑桩上的剪力和弯矩。矩形桩每根桩上设置应变片30片，圆形桩每根桩上设置应变片48片，布设示意图见图4。

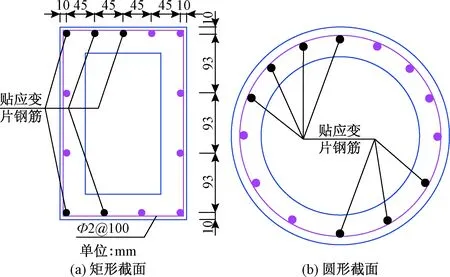
图4 不同截面空心桩应变片布设图Fig.4 Layout of the strain gauge of hollow piles of different sections

②桩身压力测试：采用土压力盒测试桩身受力。桩的自由端，压力盒埋设在内侧；桩的嵌固段，压力盒埋设在外侧；每隔10 cm埋设一个压力盒，每根桩埋设8只压力盒。布设示意图如图5。

③排水孔布置

排水孔布置如下：空心圆桩排水孔在桩后分布4排，孔间距5 cm，上、下排水孔距离桩顶、桩底均为15 cm；空心方桩排水孔在桩后分布2排，孔间距为5 cm，上、下排水孔距离桩顶、桩底均为15 cm。

1.3 试验模型设计

根据试验室现有模型槽(图6)尺寸(3 m×2 m×1 m)设计制作滑体模型，待抗滑桩滑体模型、位移传感器、土压力盒以及桩上应变片制作和安装完毕稳定后，利用布置于滑坡后缘的千斤顶对其进行水平加载，加载分级进行。在加载的过程中，用静态数据采集仪持续地存储相关数据，直至模型完全破坏。在上述模型槽上铺设约40 cm厚的砂岩板作为滑床，然后在此滑床表面铺设一层厚约2 cm的红黏土作为滑带。滑面倾角10°，滑体尺寸3 m×2 m；滑体采用砂岩板材堆砌而成，板材之间用素混凝土粘结；试验桩体按照前述设计，采用钢筋混凝土制作。按照上述过程制作好滑床、抗滑桩模型后，按照设计将其组装为试验模型(图6)。

图6 组装好的试验模型Fig.6 Assembled test model

(4)数据采集

数据采集是通过测试试件—传感器—数据采集仪器—计算机等连接流程实现的。应变片、土压力盒、位移计分别是采用1/4桥、半桥、全桥的形式与采集系统连接在一起。而采集系统与计算机的连接是通过专业的数据采集软件实现人机互动的。

2 实验结果分析

2.1 不同截面桩身弯矩分析

试验中所采集到的数据为实测拉力K，需将其换算成用于分析的相关物理量。换算目标为弯矩，公式如下[11～15]：

矩形截面桩身弯矩与应力换算公式：

K=C=α1fcbx；M=K(h0-x/2)

(1)

圆形截面桩身弯矩与应力换算公式：

M=Kπr3/4

(2)

式中：K——单根受拉钢筋的拉力/kN；

C——受压区混凝土承受的压力/MPa；

fc——混凝土轴心抗压强度设计值/MPa；

α1——强度与受压区混凝土最大应力fc的比值；

b——截面宽度/m；

x——按等效矩形应力图计算的受压区高度/m；

M——抗滑桩的抵抗弯矩/N·m；

h0——截面有效高度/m；

r——圆形截面抗滑桩半径/m。

通过数据采集系统，获取了多组实验数据，运用式 (1) 和 (2) 对实验数据进行换算，获得各测点的弯矩值，整理相关曲线如下:

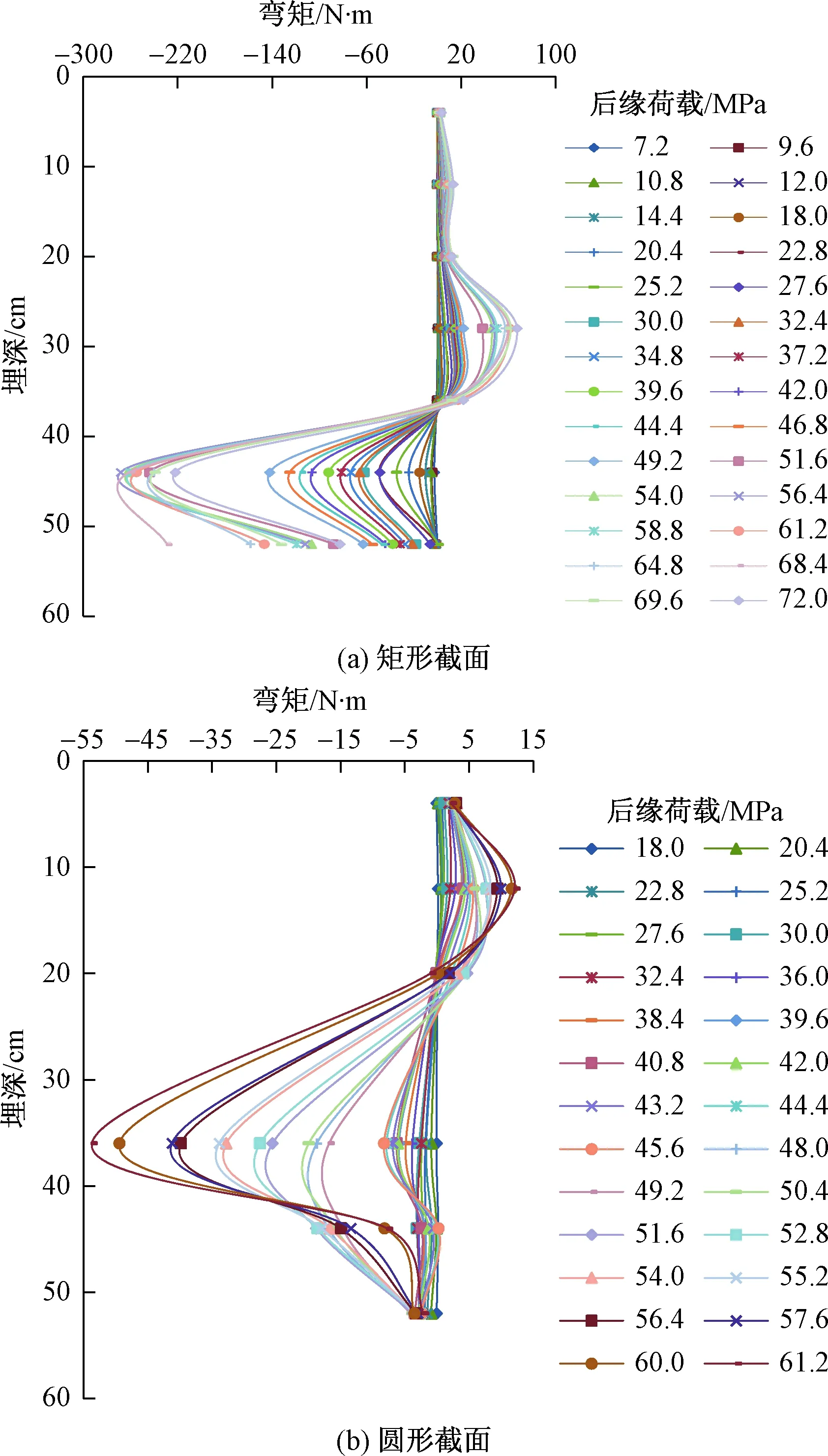
图7 不同截面空心桩桩前弯矩与埋深关系Fig.7 Diagram showing the relation of the bending moment before pile and buried depth of hollow piles of different cross sections

通过桩前弯矩分布图(图7)可以看出：两类空心桩前弯矩整体上呈对三角形分布，体现出随着荷载增加弯矩同步增加的特征，呈现出较均匀增加的特点。不同之处在于，在各级荷载下，矩形截面空心抗滑桩弯矩在桩顶至桩顶下1/3桩长处弯矩值很小，近乎为零；过了桩顶以下1/3后，弯矩开始均匀增加，反弯点出现在滑面位置附近，在滑面下0.5 m处出现最大值，约为280 N·m。圆形截面空心抗滑桩弯矩值随荷载增加自桩顶处开始均匀增加，反弯点出现在桩顶下1/3桩长处，在滑面以上0.5 m处出现最大值，约为55 N·m。

通过桩身弯矩分布图(图8)可以看出：矩形截面抗滑桩在荷载小于200 MPa时，桩身弯矩值较小，随桩埋深呈不规则的线性分布，随着荷载逐渐增大，当荷载大于200 MPa，桩身弯矩随桩埋深逐渐变为指数分布；圆形截面抗滑桩在荷载小于100 MPa时，桩身弯矩值较小，随桩埋深呈不规则的线性分布，当荷载大于100 MPa，桩身弯矩随桩埋深逐渐变为指数分布。

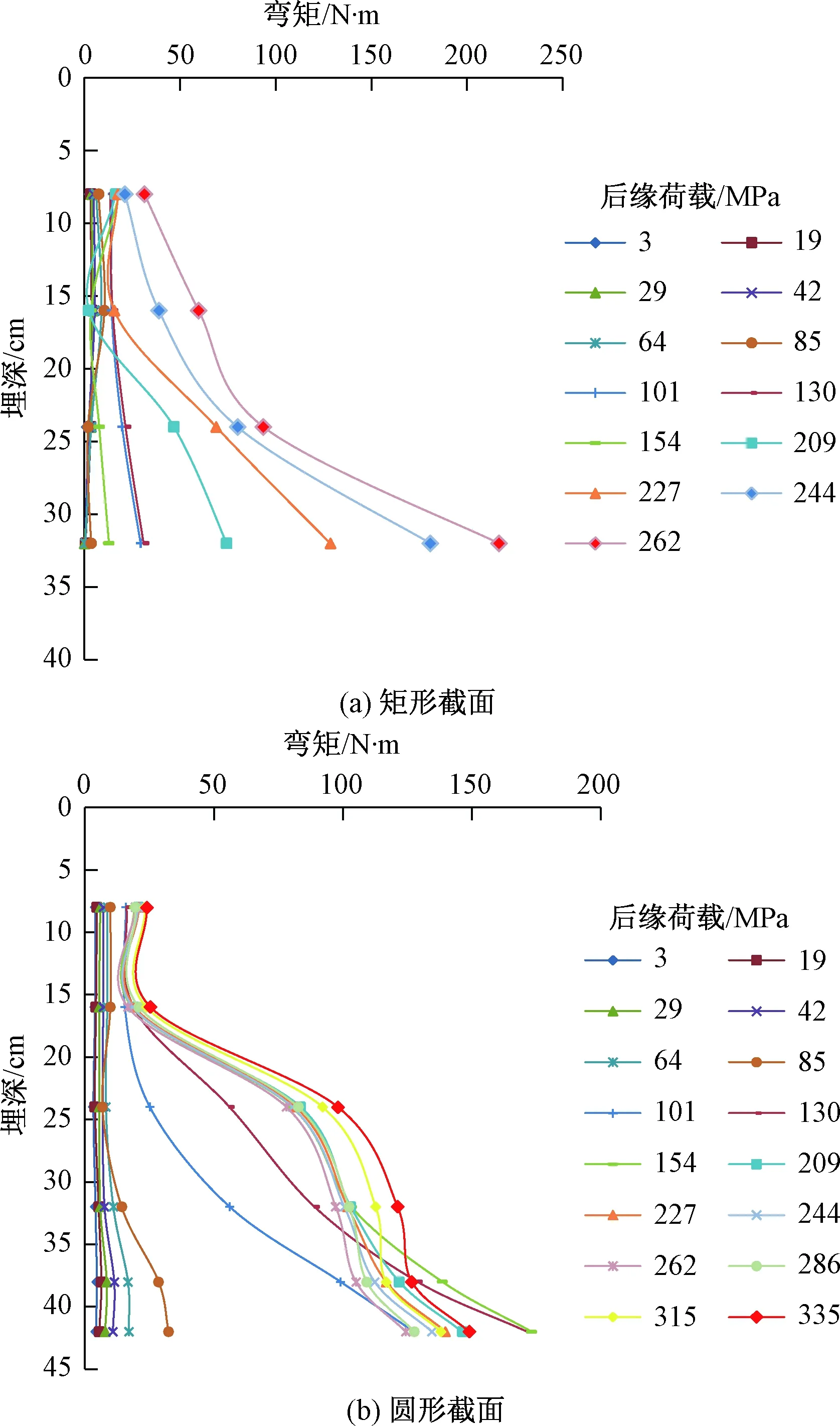
图8 不同截面空心桩桩身弯矩与埋深关系图Fig.8 Diagram showing the relation of the pile bending moment and buried depth of hollow piles of different cross sections

分析认为：桩身弯矩呈线性分布，主要是因为荷载初始缓慢施加过程中，滑体裂隙及桩身混凝土内部的空隙逐渐闭合，传递到桩内钢筋应力计的荷载非常小，所以弯矩变化不大；而随着荷载逐渐增大，当依靠钢筋来承担主要抗滑作用时，弯矩随埋深增加就逐渐变为指数分布。

综上对比分析可以看出，矩形截面空心抗滑桩最大弯矩可达280 N·m，而圆形截面空心抗滑桩破坏弯矩最小时为54 N·m，最大时为170 N·m；同时，圆形截面空心桩在荷载施加100 MPa时就转为指数分布，而矩形截面空心桩是在200 MPa才开始转为指数分布的。由此可见，矩形截面空心抗滑桩的抗弯能力优于圆形截面空心抗滑桩。

2.2 不同截面桩身应力分析

通过桩身应力分布图(图9)可以看出：矩形截面空心抗滑桩和圆形截面空心抗滑桩桩身应力均随着滑坡推力的增加大致呈现出加速的增加趋势，同时，矩形截面空心桩和圆形截面空心桩所贴3#、4#、5#应变片测得的应力较其它测点应力大，而此测点正是位于滑面处及滑面上、下两个测点。这说明在滑面上、下8 cm这段出现应力集中现象。

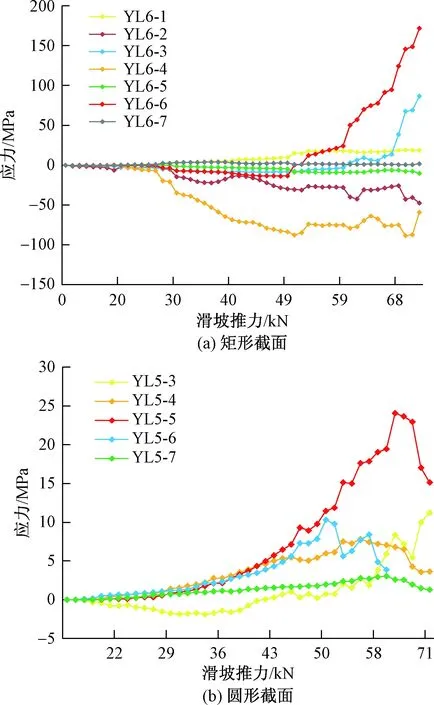
图9 不同截面空心桩桩身应力与滑坡推力关系图Fig.9 Diagram showing the relation of pile stress and landslide thrust of hollow piles of different cross sections

不同之处在于，矩形截面空心桩在荷载增大到62 kN时，应力集中段压力表现为明显的加速增长，同时桩身最大应力达到170 kN；而圆形截面空心桩在荷载44 kN时，应力集中段压力便表现为明显的加速增长，桩身最大应力为25 kN。

综合以上桩身应力的对比分析可以看出：矩形截面空心抗滑桩能承受更大的滑坡推力，具有更好的抗滑效果，但矩形截面空心桩和圆形截面空心桩空心方桩和空心圆桩均是在滑面上下8 cm段出现应力集中。实际工程中，可适当增强该段位置的配筋。

2.3 集水孔布置前后弯矩对比分析

由于矩形截面空心抗滑桩的抗滑效果和抗弯能力明显优于圆形截面空心抗滑桩，所以，只针对矩形截面空心抗滑桩集水孔布置前后的弯矩做对比试验。试验选取交错布孔、竖排直线布孔和不布孔三种情况下的桩体破坏时的桩身应力(图10)。空心桩桩体内的水采用虹吸排水装置排出，当桩体内水位上涨致触发装置的浮球位置时，虹吸装置便启动，开始排水，抽出桩孔内的水。

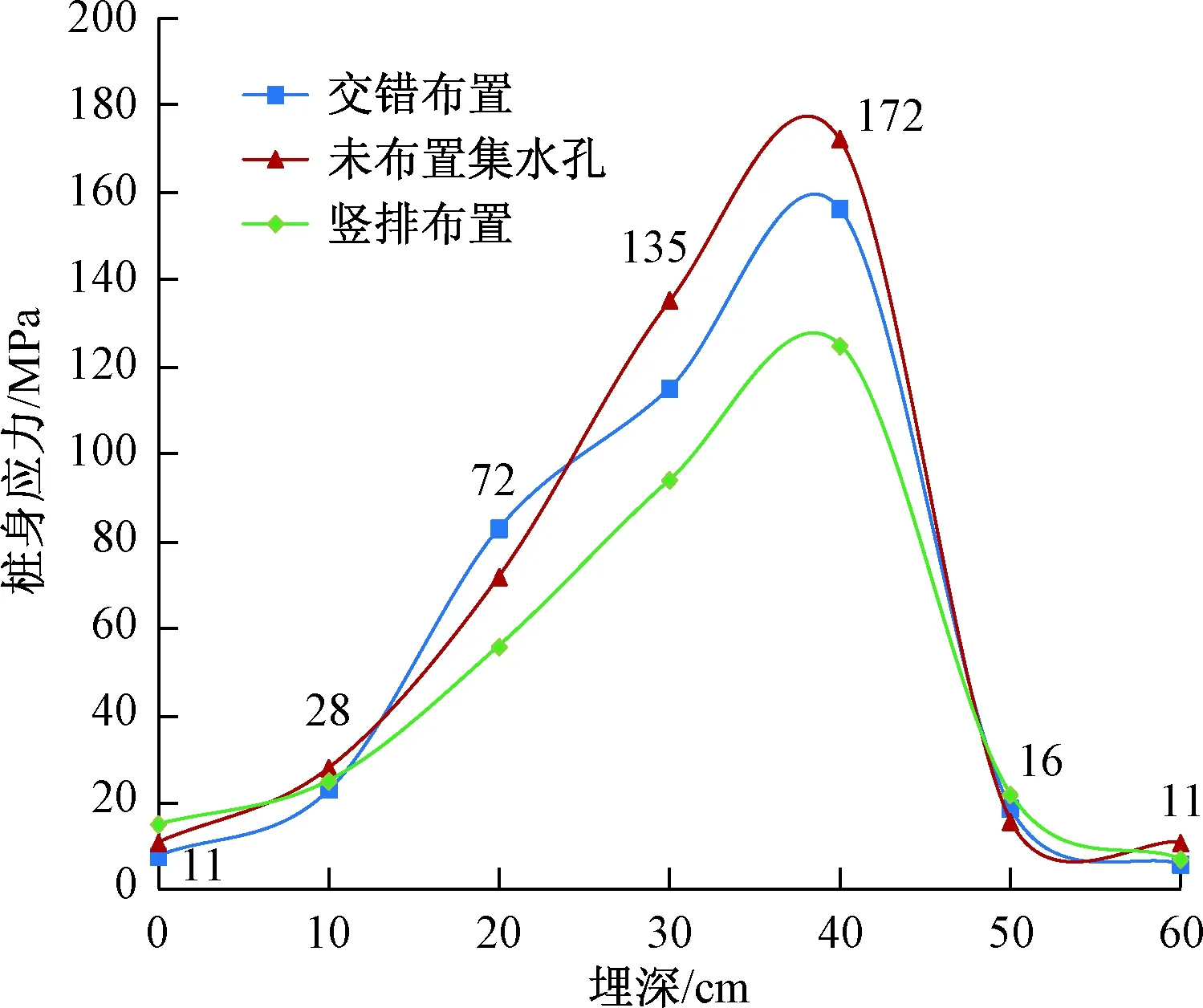
图10 布置集水孔前后桩身应力变化曲线Fig.10 Stress curve of pile body before and after arranging water hole

通过分布曲线关系(图10)可以看出：在未布置集水孔时，桩体发生破坏时滑面位置受到的应力约172 MPa；交错布置集水孔时，桩体发生破坏时滑面受到的应力约为155 MPa；竖排直线布置集水孔时，桩体发生破坏时滑面受到的应力约132 MPa。因此可以看出，布置集水孔前后对桩体承载能力有一定的影响，导致承载能力有所降低，交错布置集水孔时，承载力约降低10%，竖排直线布置承载力约降低25%。

综上分析，在工程选用空心桩工程时，应首先考虑水对边坡稳定性的影响大小，确定是否需要布置集水孔来减小滑坡推力，若需要，则宜采用交错布置的方式。

2.4 破坏特征分析

试验完成后，分别观察桩体破坏情况。从破坏图片(图11)可以看出，圆形截面空心抗滑桩破坏程度明显严重些，桩体在沿着滑面附近位置被完全剪断，剪切位移达15 cm；从矩形截面空心抗滑桩破坏形态看出，桩体基本没有被剪断，只是在桩底端出现局部的破坏，但是桩身出现两条沿着排水孔贯穿的裂缝，这说明桩在沿着排水孔布置位置抵抗变形能力最弱，出现应力集中现象，导致形成贯通性裂缝。

通过以上分析，矩形截面空心抗滑桩主要表现为受挤压破坏形态，而圆形截面空心抗滑桩表现为沿滑面处受剪而破坏的形态。

图11 不同截面空心桩的破坏形态Fig.11 Failure pattern of hollow piles of different cross sections

3 数值模拟分析

3.1 计算模型

为了进一步验证试验结果，本文采用Midas/GTS 有限元软件进行前期地层网格模型的生成，借助Midas/GTS导入FLAC3D中的接口程序，将在Midas/GTS软件中建立好的地层网格模型导入到FLAC3D中[16]，形成如下矩形截面空心桩和圆形截面空心桩数值模型(图12)。

图12 不同截面空心桩数值模型图Fig.12 Numerical model of hollow piles of different cross sections

3.2 计算参数

通过试验材料配比计算及相关经验值，选取计算参数见表2。

表2 计算参数取值Table 2 Values of the calculated parameters

3.3 计算结果分析

利用以上模型和参数，将抗滑桩设置为弹性模型，并改变相应参数，计算得到模型的位移云图(图13)及桩体的受力云图(图14)。

通过图13可以看出，在相同的荷载和参数条件下，矩形截面空心桩模型滑体后部位移量约15～17.5 mm，前缘位移量约为10～12.5 mm；而圆形截面空心桩模型滑体后部位移约为27.5～32.5 mm，前缘位移量也达到22.5～25 mm；

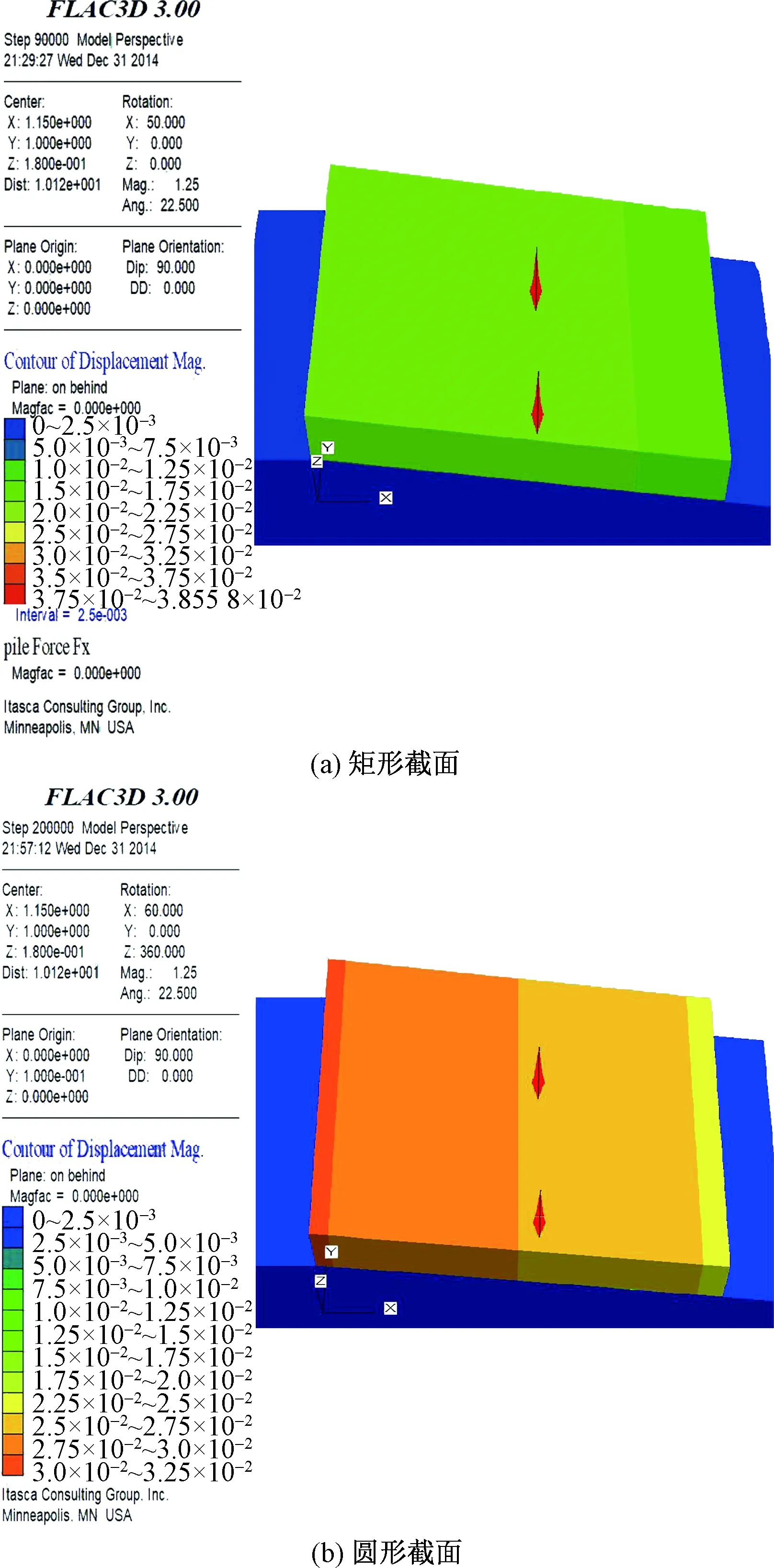
图13 不同截面空心桩模型整体位移云图Fig.13 Overall displacement cloud map of hollow piles of different cross sections

对比两者位移量可以发现：在相同荷载和参数条件下，圆形截面空心桩模型滑体的后部位移和前缘位移均明显大于矩形截面桩，进一步说明了矩形截面空心桩对坡体的支挡效果优于圆形截面空心桩，这也与室内模型实验的结果较一致。

通过模拟获得的两类截面桩体的受力云图(图14)，可以发现，矩形截面空心桩和圆形截面空心桩的最大受力部位均出现在滑面位置附近处，即滑面位置附近受到的支撑力最大；再对比桩体受到的最大支撑力，矩形截面桩体受到的最大支撑力为3 268 kN,而圆形截面最大支撑力为3 048 kN，这也说明了矩形截面的承载能力更好。

图14 不同截面空心桩桩体受力云图Fig.14 Stress nephogram cloud map of hollow piles of different cross sections

同时，通过观察两类桩体的受力分布，自由端支撑力随着桩顶往下逐渐增大，在滑面位置附近达到最大值；再随着进入锚固段至桩底部，支撑力逐渐变小，只是上部自由端支撑力的变化速率小于下部锚固段支撑力变化速率，这也与室内试验获得桩体弯矩效果一致。

4 结论

(1)在桩体结构上，矩形截面空心桩体的承载能力优于圆形截面空心桩体。

(2)桩身最大弯矩分布在滑面上下约5 cm处，分布范围约占桩体自由段长度的1/4～1/2范围，建议在设计中加强桩底至滑面以上1/2范围内的结构配筋。

(3)空心桩增加集水孔布置后，由于设孔位置会出现应力集中，对桩体承载能力有一定影响，集水孔直线布置时的影响大于集水孔交错布置时的影响，交错布置时，桩体承载能力与未布置集水孔的桩体比较，承载能力约下降10%。

(4)对于圆形空心桩，试验发现，采用偏心截面设计的圆形桩的承载能力明显高于采用同心圆截面设计的圆形桩，建议后期加强对偏心截面桩设计方法的研究。

总之，圆形截面空心抗滑桩和矩形截面空心抗滑桩在边坡治理过程中各有优势，圆形截面空心抗滑桩在抗滑效果与承载力方面不及矩形截面空心抗滑桩，但其具有施工条件要求低、成孔快、便于机械化施工等特点，使其在边坡应急抢险领域具有较大的应用空间。因此，是实际工程中，应结合具体的案例条件，选择合适的桩形。