考虑摩擦条件下临近既有建筑物的有限土体土压力上限解

胡卫东，曹文贵，曾律弦，刘晓红

(1.湖南理工学院土木建筑工程学院，湖南 岳阳 414006；2.湖南大学岩土工程研究所，湖南 长沙 410082)

土压力计算是岩土工程挡土墙和支护结构设计的一个重要内容，通常假定墙后填土为半无限连续土体，采用经典朗肯、库伦土压力理论公式或修正经验公式进行计算[1]。然而，随着城市地下空间被广泛利用，地下建(构)筑物越来越密集，挡土墙和支护结构前后大量出现有限宽度土体，特别是临近既有地下室的基坑支护结构、城市地铁及市政管网工程建设中的临时支挡结构等[2～3]。有限宽度土体边界条件不满足半无限体的基本假定条件，其破坏机理和破坏模式已产生较大变化，按传统方法计算结果与实际值存在较大差异，因此，简单套用经典土压力理论计算有限宽度土体土压力显然是不合适的，研究有限宽度土体土压力计算模型具有重要的理论研究和工程应用价值，这也是本文研究的出发点。

已有学者开展刚性挡土墙有限宽度土体主动土压力与被动土压力的理论研究，取得了比较丰硕的研究成果，其中最常采用的方法是极限平衡方法。Handy[4]通过对挡土墙侧的土体单元进行应力分析，获得两竖直粗糙挡土墙后有限宽度填土土压力的分布计算公式；Frydman等[5]、Take等[6]结合模型试验研究了邻近基岩面且填土为砂砾土的刚性挡土墙在静止和主动土压力状态下的侧向土压力；Greco[7]提出重力式挡土墙后有限宽度填土破坏过程的三种破坏模式，推导出主动土压力的分析计算模型；马平等[8]假定滑裂面为平面，利用极限平衡方法，考虑土的黏聚力影响，建立了土压力计算模型和滑裂面破坏角的数学表达式；杨明辉等[9～10]提出了直线破裂面模式和曲线破裂面模式，并建立了相应有限土体主动土压力的求解方法；王闫超等[11]假定平面滑裂面模式，采用薄层单元法推导了刚性挡土墙无黏性有限土体主动土压力的解析解；应宏伟等[12～14]研究了邻近地下室外墙和狭窄基坑平动模式下刚性挡土墙主动土压力和被动土压力分布模型；岳树桥等[15]利用筒仓原理，通过静力平衡条件求解微分方程得到了相邻基坑有限宽度土体的主动土压力计算公式；静力平衡方法概念明确，计算简便，但经常需要假定滑动面和应力分布状态。

近年来，部分学者利用数值模拟开展刚性挡土墙有限土压力的研究，徐超等[16]采用FLAC软件建立有限填土加筋土挡墙的二维数值模型，讨论了加筋间距、加筋长度以及墙面与竖直平面的夹角对挡墙稳定性和破坏模式的影响；朱伟等[17]、应宏伟等[12～13]利用有限元软件研究了平动模式下挡墙后土体变形规律和土压力分布模式；Yang[18]针对有限宽度土体离心模型试验结果开展了有限元分析模拟；Chi-cheng Fan[19]针对有限宽度填土后方为基岩面的情况，利用有限元数值模拟刚性挡土墙主动土压力分布。数值分析方法研究在很大程度上丰富和验证了理论研究成果，但在土体本构模型与力学参数选择上仍存在不确定性。

极限分析法分析挡土墙与支护结构土压力不需要准确确定破坏机构中各刚性块体内部的应力分布，在岩土工程中已得到广泛应用，然而，具体到刚性挡土墙有限土体土压力理论研究却相对较少。高印立[20]基于塑性极限分析理论，推导出平面滑裂面模式下有限土体主动土压力和被动土压力的计算公式；谢小荣等[21]针对公路工程中经常出现的路堤与切坡工程挡土墙，通过极限分析虚功原理建立了边坡中有限宽度土体主动土压力计算公式；廖俊展等[22]通过极限分析上限理论，研究基坑工程中有限土体主动土压力，并探讨了其与朗肯土压力计算值的差异。挡土墙墙背作用摩擦力时侧向土压力的确定，一直是土力学的一个传统稳定问题，以上学者采用极限分析方法研究均假设临近建(构)筑物的刚性挡土墙背竖直光滑，没有充分考虑到挡土墙与土之间及建(构)筑物与土之间的摩擦作用，存在很大不足，这也是本文须重点解决的问题。

综上所述，现有关于刚性挡土墙有限土压力研究仍存在不同程度的问题和局限性，有必要进行进一步研究，为此，本文将从刚性挡土墙和支护结构有限土体的工程特征入手，考虑挡土墙与土之间及建(构)筑物与土之间的摩擦力、挡土墙背倾角及填土顶面竖向荷载等影响，基于挡土墙的平动模式，利用极限分析上限定理，并在土压力上限求解中引入摩擦能耗计算，探讨有限土压力分析新方法，以期完善有限土压力理论。

1 基本假定

根据刚性挡土墙和支护结构有限宽度土体的工程特征，为便于采用极限分析上限法计算，先作如下基本假定[8～14]：

(1)挡土墙后填土材料为理想刚塑性体，由于填土顶面超载作用而不考虑坡顶的张拉裂缝；

(2)挡土墙土压力问题可视为平面应变问题，达到主动和被动极限状态时形成直线滑裂面；

(3)滑动区域内土体在达到塑性极限平衡状态时服从Mohr-Coulomb屈服准则和相关联流动法则；

(4)考虑挡土墙墙背面为粗糙面，挡土墙与填土之间及建(构)筑物与土之间的外摩擦角为δ。

2 有限土体主动土压力计算

2.1 计算模型

如图1所示，设挡土墙高H，墙背倾角为θ；填土为有限宽度，其宽度为b，其上作用均布超载q；填土表面水平，填土材料为均质土体，内摩擦角为φ，黏聚力为c；在土体重力作用下滑块ABED沿ED滑裂面相对于墙体向下和向外滑动，ED面与水平面夹角为β；按照相关联流动法则，滑动速度Va与ED面成φ角[23]。

图1 粗糙倾斜墙背的主动土压力Fig.1 Reinforcement distribution modes of active earth pressure

在上述几何计算模型基础上，根据速度相容的闭合三角形几何关系，可得到如图2(a)所示破坏机构的运动速度关系，再由矢量分析原理及速度相容性要求可以推导出各速度间断面上速度[24]。

图2 主动土压力的极限分析速度场Fig.2 Velocity field of active earth pressure

(1)

(2)

式中：V1——挡土墙水平方向的运动速度；

V2——墙背面AD速度间断面上的间断速度。

2.2 内能耗散

(3)

Pan=Pacosδ

(4)

式中：Pan——主动土压力合力对墙背AD面的垂直分量；

Pa——墙背AD面上反力，即主动土压力合力，与AD面的法线成δ角，并作用在法线下方。

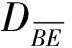
(5)

(6)

L=H-(b-Hctgθ)tanβ

(7)

式中：Pj——主动土压力；

Ka——朗肯主动土压力系数；

L——BE面高度。

(8)

2.3 外力功率

此研究问题的外力包括自重力、超载和主动土压力，各外力功率具体计算方法如下：

(1)q外力功率Wq：

Wq=qbVasin(β-φ)

(9)

(2)主动土压力Pa所做功率WPa：

(10)

(3)土体滑块ABED自重力W所做功率WⅠ：

WⅠ=γSABEDVasin(β-φ)

(11)

(12)

式中：SABED——滑块ABED的面积。

使内部能量耗散率与外功率相等，得到：

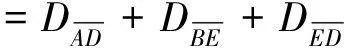
(13)

(14)

f1=qb+γSABED-Pjtanδ

(15)

(16)

f3=sinδsin(β-φ)+sin(θ-δ)sin(β+θ-φ)

(17)

3 有限土体被动土压力计算

3.1 计算模型

如图3所示，在挡土墙被动土压力作用下滑块ABED沿ED滑裂面相对于墙体向上向内滑动，ED面与水平面夹角为β；同理，滑动速度Vp与ED面成φ角。

图3 粗糙倾斜墙背的被动土压力Fig.3 Reinforcement distribution modes of passive earth pressure

图4 被动土压力的极限分析速度场Fig.4 Velocity field of passive earth pressure

同样，根据速度相容的闭合三角形几何关系(图4)，可以求出各速度间断面上速度：

(18)

(19)

式中：V3——挡土墙水平方向的运动速度；

V4——墙背AD面上的间断速度。

3.2 内能耗散

(20)

Ppn=Ppcosδ

(21)

式中：Ppn——被动土压力合力对墙背面的垂直分量。

Pp——被动土压力合力，与AD面的法线成δ角，并作用在法线的上方。

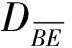
(22)

(23)

式中：Pk——主动土压力；

K0——静止土压力系数。

(24)

3.3 外力功率

(1)q外力做负功，其功率Wq：

Wq=-qbVpsin(β+φ)

(25)

(2)被动土压力Pp所做功率WPp：

(26)

(3)土体滑块ABED自重力做负功，其功率WⅠ：

WⅠ=-γSABEDVpsin(β+φ)

(27)

使内部能量耗散率与外功率相等，得到：

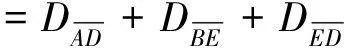
(28)

(29)

f4=qb+γSABED+Pjtanδ

(30)

f5=sin(θ+δ)sin(β+θ+φ)-sinδsin(β+φ)

(31)

4 破裂面与土压力公式求解

5 算例分析

5.1 算例一(主动土压力)

为验证本文方法的合理性，采用文献[3]算例进行主动土压力计算，并与朗肯主动土压力进行比较。该工程在距两层地下室外墙b=2 m远的地方开挖基坑，深度为H=10 m，土层为均质黏土层，土层重度γ=19 kN/m3，内摩擦角φ=15°，黏聚力c=10 kPa，墙土间外摩擦角为tanδ=0.25，填土面水平，上面作用超载q=20 kPa。

文献[3]采用极限平衡方法，基于平动模式，考虑了挡土墙与土体间粘结力进行计算，由图5可知，本文计算结果与其计算结果较接近，且变化规律基本相同；随着深度增大，本文方法及文献[3]方法计算有限土体主动土压力合力值较无限土体朗肯土压力合力值差值增大，这也说明无限土压力计算理论已经不适合有限宽度土体；图6为本文方法计算不同宽度土体的Pa-H关系曲线图，反映出有限土体宽度一定时随着计算深度增加，主动土压力合力增大。

图5 b=2 m时的Pa-H关系曲线Fig.5 Relationship between Pa and H with b=2 m

图6 不同宽度土体的Pa-H关系曲线Fig.6 Relationship betwwen Pa and H with different widths

结合本工程实例进行参数分析，重点考察有限土体宽度b及挡土墙倾角θ及墙土间外摩擦角δ等参数对破裂角β的影响。由图7可知，随着有限宽度b增大，极限破裂角β非线性减小；由图8可知，随着挡土墙倾角θ增大，极限破裂角β非线性减小；同时也可看出墙土间外摩擦角δ在0～φ之间变化对破裂角影响较小。有限土体主动土压力计算模型中的破裂角不再是经典理论的45°+φ/2，而是一个不确定值，其值随着土的力学参数、计算深度、有限土体宽度及挡土墙倾角等变量变化而变化。由图9可知，随着计算宽度b增大，主动土压力合力Pa增大，且逐渐趋于稳定值；由图10可知，随着挡土墙倾角θ增大，主动土压力合力Pa减小；同时也可看出，墙土间外摩擦角对土压力合力值影响较大。

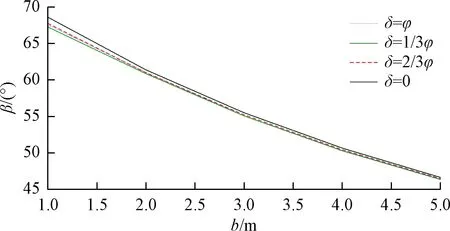
图7 β与b的关系曲线Fig.7 Relationship between β and b

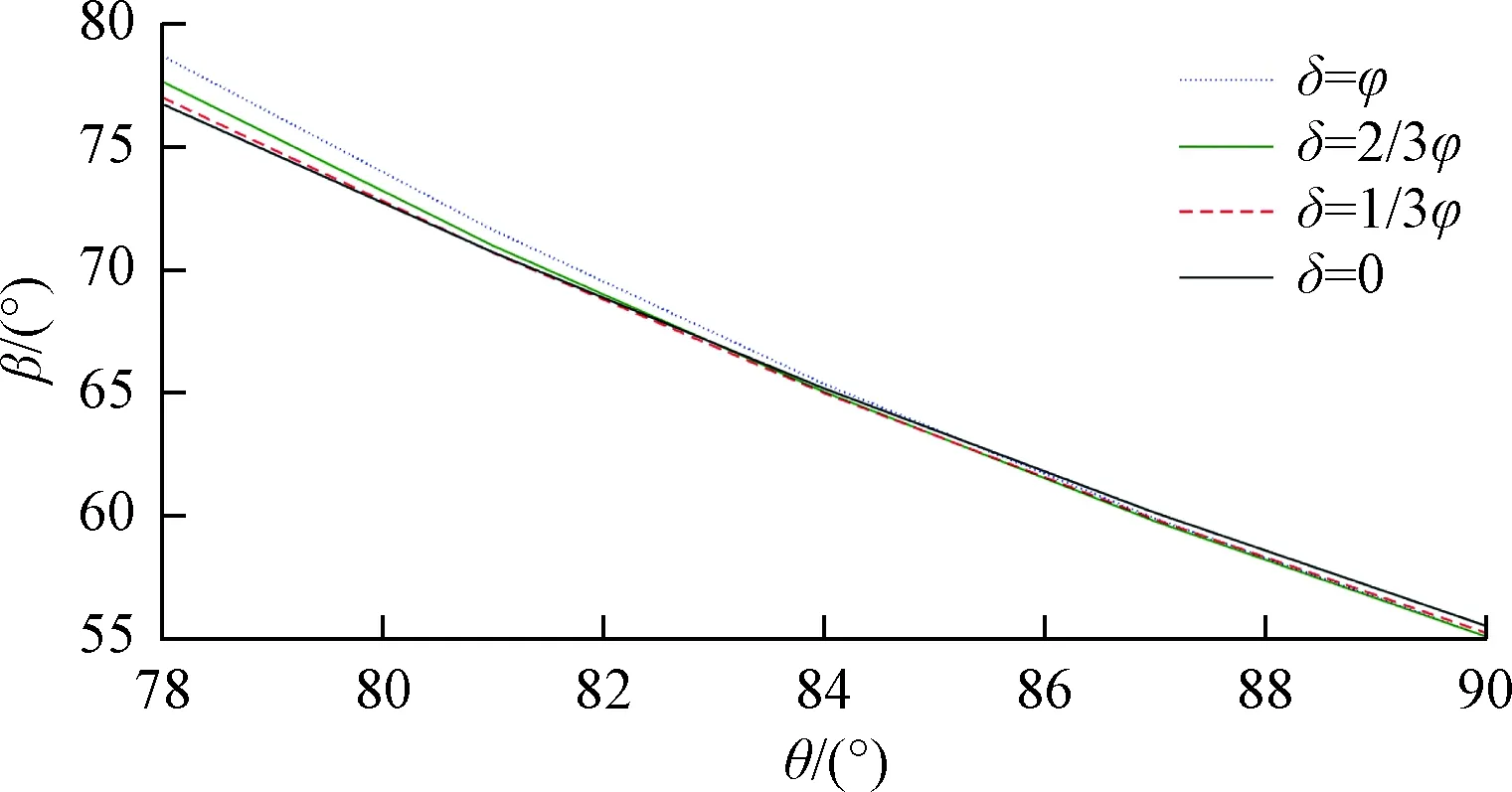
图8 β与θ的关系曲线Fig.8 Relationship between β and θ

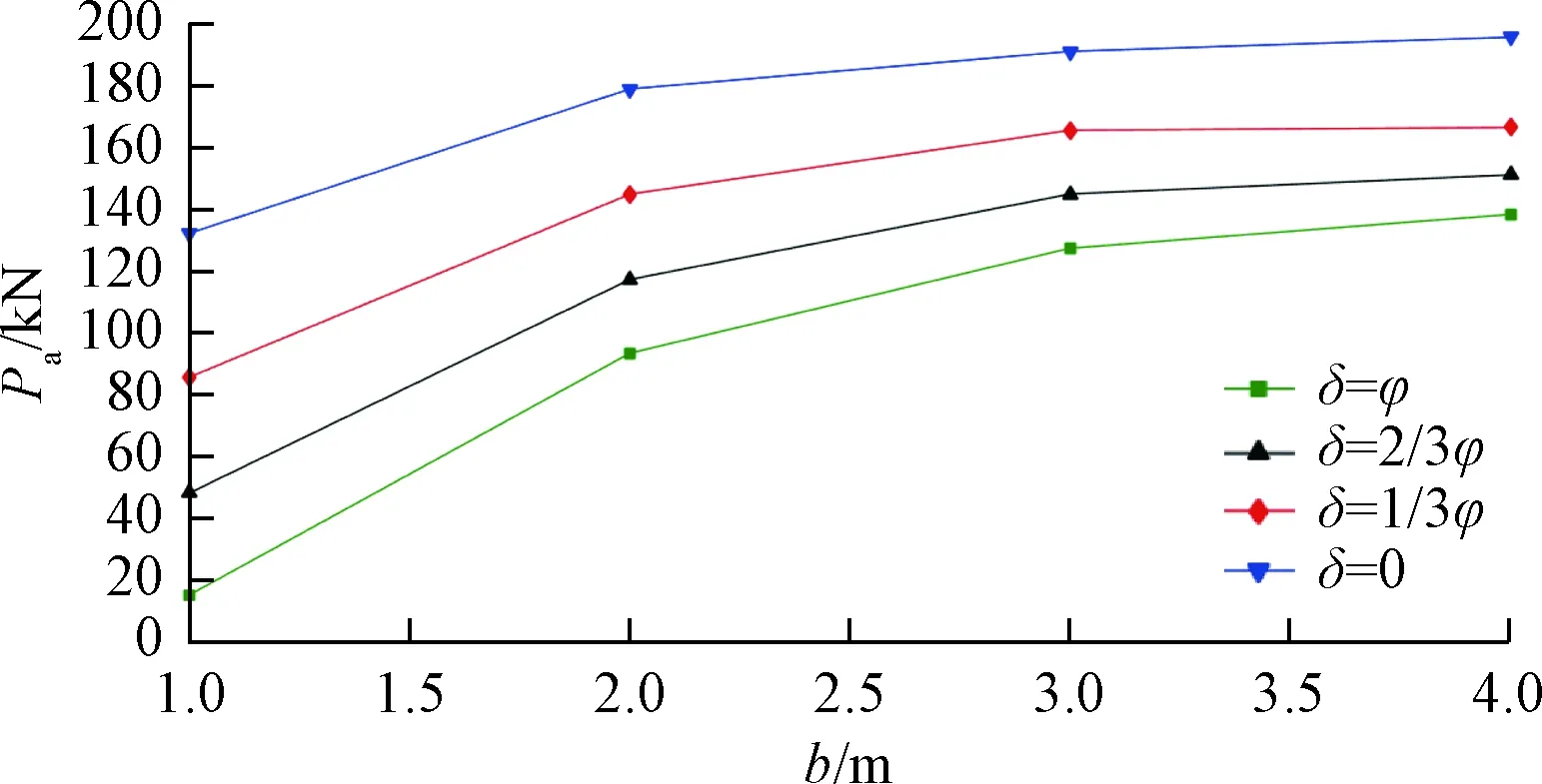
图9 Pa与b的关系曲线Fig.9 Relationship between Pa and b

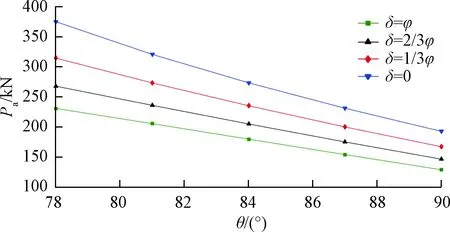
图10 Pa与θ的关系曲线Fig.10 Relationship between Pa and θ

5.2 算例二(被动土压力)

设有限土体宽度b=2 m，深度为H=8 m，无黏性砂土层，重度γ=20 kN/m3，内摩擦角φ=30°，墙土间外摩擦角为δ=2φ/3，挡土墙背竖直，填土面水平，静止土压力系数K0=0.3。采用本文方法计算有限土体被动土压力合力并与经典朗肯、库伦土压力理论计算结果进行比较，如图11所示。由图11可知，有限宽度土体被动土压力合力随着深度增大远小于库伦被动土压力；相比朗肯理论计算结果，本文方法在计算深度较小时的被动土压力值大于朗肯被动土压力值。图12为本文方法计算不同宽度土体的Pp-H关系曲线图，从图12中亦可看出，随着计算深度增大时，有限土体宽度越大则被动土压力越大。

图11 不同方法计算的Pp-H关系曲线Fig.11 Relationship between Pp and H with different methods

图12 不同宽度土体的Pp-H关系曲线Fig.12 Relationship between Pp and H with different widths

6 结论

(1)本文从临近建(构)筑物有限宽度土体的工程特性出发，考虑挡土墙与土之间及建(构)筑物与土之间的摩擦作用，挡土墙背倾角及填土顶面竖向荷载等的影响，引入上限定理，计算粗糙挡土墙及建(构)筑物与土界面间的摩擦能耗，从而建立了有限宽度土体主动土压力和被动土压力分析模型。

(2)主动极限状态下破裂角是一个不确定角，其随着计算深度增大而非线性增大，随有限土体宽度和挡土墙背倾角增大而非线性减小；主动土压力合力小于朗肯主动土压力，随墙土间外摩擦角、挡土墙背倾角及有限土体宽度增大而增大；被动土压力合力随着计算深度不断增大而远小于库伦被动土压力合力值。

(3)墙土间外摩擦角对破裂角影响较小，而对土压力合力影响较大。