基于尖点突变理论的岩溶区嵌岩桩溶洞顶板安全厚度研究

梁冠亭，肖开乾，郑宏伟，夏文辉

(1.武汉市市政建设集团有限公司，湖北 武汉 430056；2.武汉大学土木建筑工程学院，湖北 武汉 430072)

我国岩溶地质分布广泛、岩溶地质状况复杂多样，在岩溶区开展基础设施建设时，桩基础因其承载力高、沉降小等特点被广泛应用于西部山区的桥梁工程建设中。而溶洞顶板安全厚度的计算是工程设计的关键技术之一，因此开展岩溶区嵌岩桩溶洞顶板安全厚度的研究对实际工程的指导具有重要的意义。

目前，国内众多学者针对该问题开展了大量的研究，且在试验研究、数值研究及理论研究方面都取得了较为丰硕的成果。在试验研究方面，赵明华等[1]根据相似理论，设计了溶洞顶板破坏模式的大比例模型试验，得到了不同厚度条件下溶洞顶板的破坏特性；张慧乐等[2]、张智浩等[3]基于室内模型试验，探讨了不同形状、跨径、大小的溶洞对嵌岩桩桩端承载极限承载力的影响。在数值研究方面，黎斌等[4]采用三维有限元法对嵌岩桩桩端荷载作用下溶洞顶板的稳定性进行了分析；唐炜等[5]基于有限差分软件FLAC3D，并采用强度折减法分析了溶洞顶板的稳定性和塑性区发展规律；尹凯丽等[6]则采用ANSYS软件对覆盖型溶洞进行了正交数值模拟试验。然而由于工程地质的不确定性以及计算参数选取的复杂性，使得数值方法在实际工程的应用存在局限性，因此有必要开展岩溶区嵌岩桩溶洞顶板稳定性评价理论方法的研究。蒋冲等[7]根据Mohr-Coulomb屈服准则，建立了岩溶区路基溶洞顶板安全厚度确定方法；赵明华等[8]结合桩端岩层极限状态下的传力机制，分析了岩溶区嵌岩桩桩端极限破坏模式，给出了溶洞发生冲切破坏和冒顶破坏时桩端的极限承载力计算公式。以上研究虽然已经较为系统，能较好地指导工程实践，但考虑到桩端岩层破坏的不规则、不连续及不均匀的突发特点[9]，何忠明等[10]根据极限平衡的思想，基于尖点突变理论建立了路堤填筑过程中溶洞顶板失稳判定的数学模型；赵明华等[11]、龚先兵等[12]将溶洞顶板视为固支梁，基于突变理论推得了嵌岩桩岩溶顶板安全厚度和极限承载力的计算公式。然而，潘岳等[13]认为均布荷载作用下两端固支梁结构没有跳跃失稳机制，不属于突变理论讨论范畴。

鉴于此，本文根据岩溶区嵌岩桩-溶洞体系的工程特点，将结构系统简化为顶板两端受滑动支座约束，且水平向作用地应力的平直梁模型，基于尖点突变理论分析顶板失稳破坏机制，推导了满足顶板稳定的必要条件和充分条件，求得了溶洞顶板的最小安全厚度。最后，通过工程算例验证本文方法的可行性。

1 计算模型及基本假定

对于如图1所示的溶洞顶板与嵌岩桩作用系统，控制顶板破坏的作用力有顶板自重及顶板上的荷载与地应力。取单位宽度顶板，视为如图2所示的平直梁，简化为平面应变问题处理，并做如下假定：

(1)顶板两端约束简化为滑动支座，岩体水平向地应力简化为分布荷载作用在溶洞顶板两端。

(2)溶洞顶板岩层自重及其上覆土层作用力视为均布荷载作用在顶板上。

(3)嵌岩桩视为简单的端承桩，不考虑上部桩周土侧摩阻力，桩端阻力简化为集中力作用在顶板上。

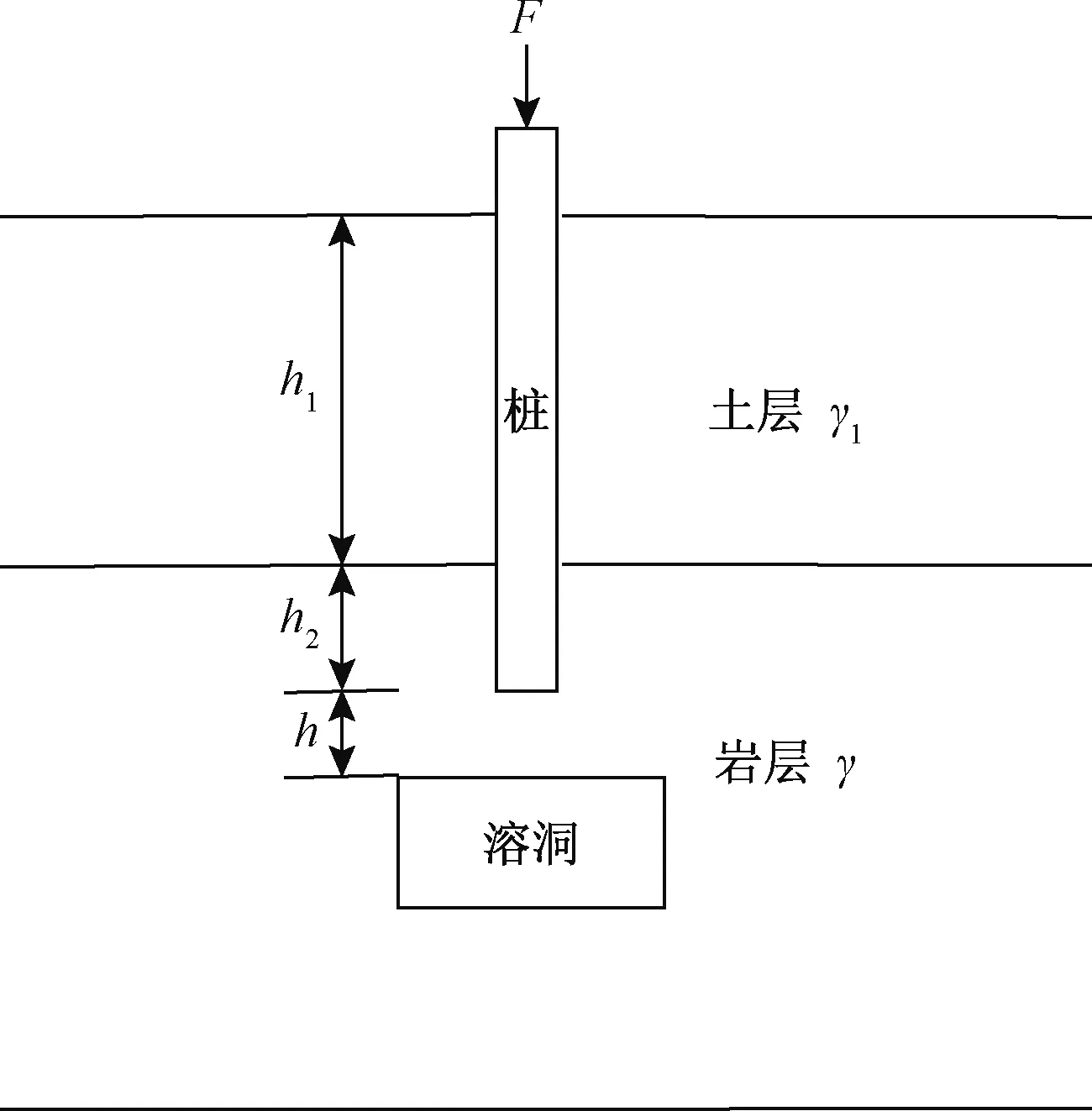
图1 溶洞顶板与嵌岩桩的作用系统Fig.1 System of cave roof and rock-socketed pile

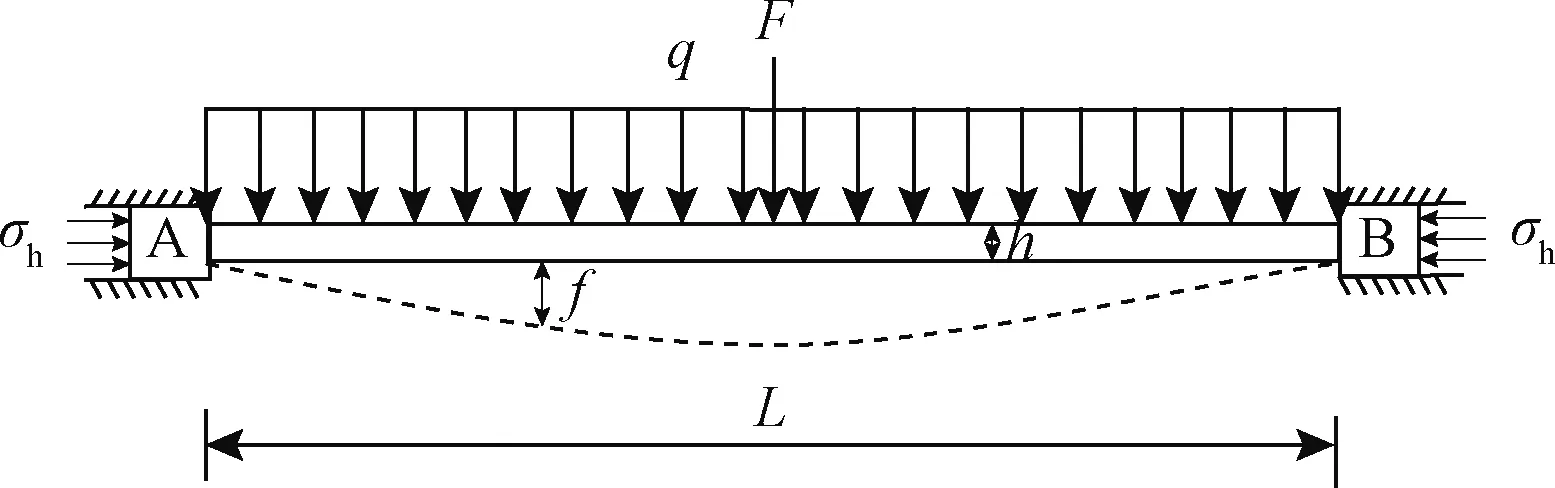
图2 溶洞顶板破坏的力学模型Fig.2 Mechanical model of cave roof failure

图1、图2中：γ1为上覆土层的自重，h1为上覆土层的厚度，γ为岩层的重度，h2为基桩嵌岩深度，h为溶洞顶板厚度，L为溶洞顶板的跨径，q为顶板岩层及其上覆土层自重，q=γ1h1+γ(h2+h)，F为桩端阻力，f为梁的挠度，σh为地应力强度，岩体的水平地应力大小N=σh·h。

2 尖点突变模型的建立

2.1 势函数

梁轴线挠曲线方程f(s)可按照傅里叶级数展开：

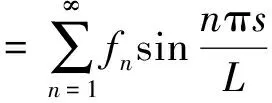
(1)

由于梁在荷载作用下发生微弯曲，结合顶板两端滑动支座的约束条件，在二级近似的条件下，梁的轴线挠曲线可近似用式(2)表示[14]：

(2)

式中：s——弧长；

Δ——梁轴线中点的挠度。

从弹性稳定理论知，梁结构的总势能为弯曲变形能与荷载势能改变量之和，即：

Ω=U-W1-W2-W3

(3)

式中：U——梁的弯曲应变能；

W1，W2，W3——均布力q、集中力F、水平力N所做的功。

梁挠度曲线在s处的曲率用弧长坐标表示为：

(4)

故梁的弯曲变形能为：

(5)

式中：D——溶洞顶板的抗弯刚度，可按式(6)计算：

(6)

式中：E，μ——顶板所在岩层的弹性模量、泊松比。

均布力q所做的功为：

(7)

集中力F所做的功为：

W2=Fδ

(8)

设梁受水平作用力N后，两端的位移为ΔL，并进行Taylor级数展开，将式(2)代入得：

(9)

积分可得水平力N所做的功：

(10)

将式(5)、(7)、(8)和(10)代入式(3)中，并略去高阶项，整理得：

(11)

2.2 尖点突变模型平衡曲面和分叉集方程

对式(11)作变量代换，令：

(12)

可得岩溶区嵌岩桩溶洞顶板结构系统势函数的标准形式：

Ω=x4+ux2+vx

(13)

式中：x——系统的状态变量；

u，v——系统的控制变量。

x，u，v构成三维空间，如图3所示。

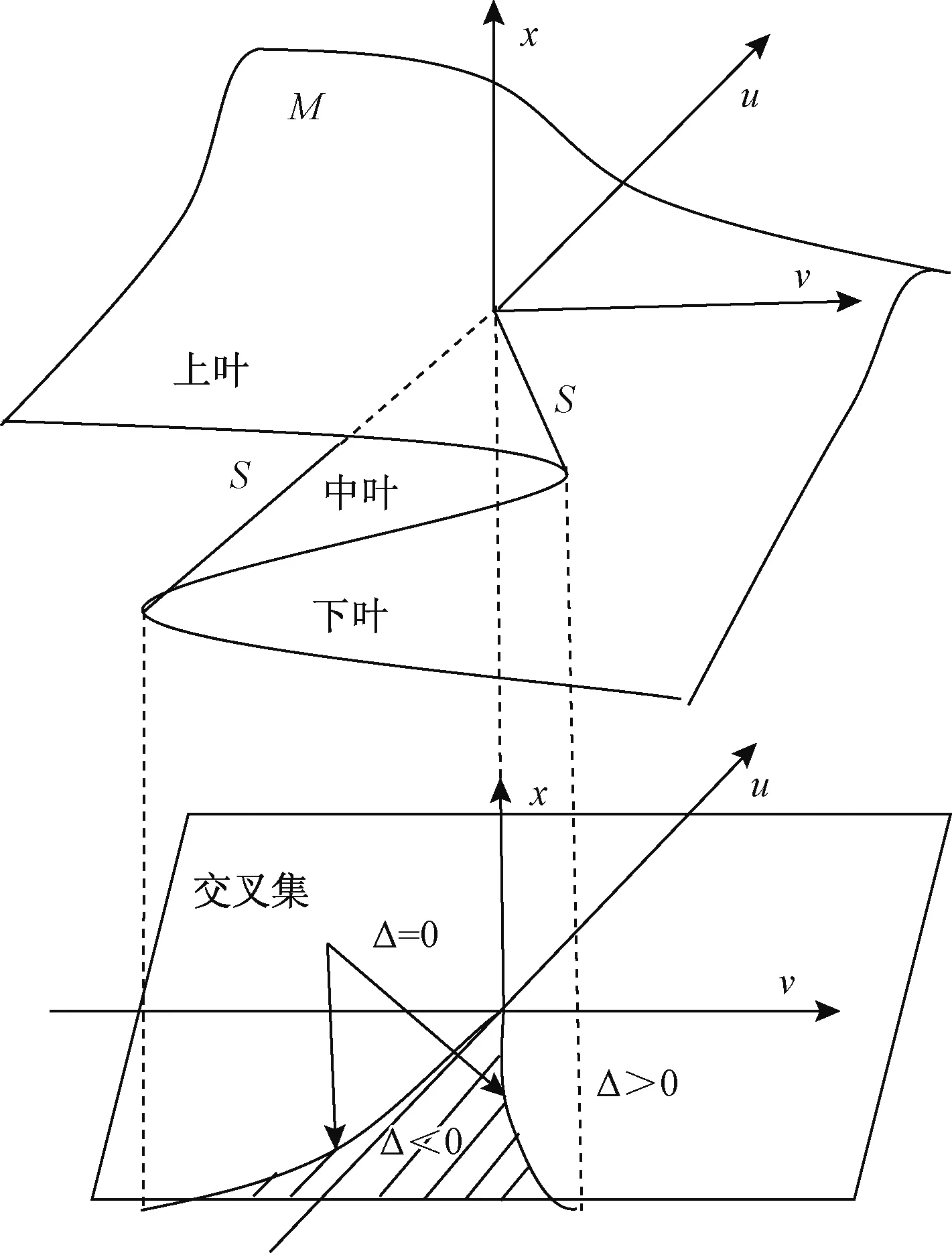
图3 尖点突变模型平衡曲线和分叉集Fig.3 Equilibrium curve and bifurcation set of cusp catastrophe model

对势函数Ω求一阶导数，得到系统作准静态形变时的平衡方程：

(14)

其图形为尖点突变模型平衡曲面M(图3)。平衡曲面M上有2条垂直切线的点集S的方程为：

(15)

S集在控制平面上的投影为分叉集(图3)。

联立式(14)、(15)消去x，即可得到结构系统尖点突变模型的分叉集方程：

Δ=8u3+27v2=0

(16)

从图3中可以看出，M分成三叶：上叶、中叶和下叶，在中叶上有：

(17)

在上叶和下叶上有：

(18)

2.3 岩体水平地应力

根据图2对溶洞顶板破坏模型的受力分析可知，溶洞顶板岩层及其上覆土层自重q、桩端阻力F以及岩体的水平地应力N是控制顶板失稳破坏的关键因素，根据张震等[15]基于李四光等学者对全国各地区地应力分布规律的推算结果，最大水平地应力σhmax和最小水平地应力σhmin可按式(19)计算：

(19)

式中：H——溶洞的埋深，H=h1+h2+h。

2.4 岩溶区嵌岩桩溶洞顶板最小安全厚度

(1)岩溶区嵌岩桩溶洞顶板稳定的必要条件

由图3可知，只有当u≤0，式(14)才有实数解，此时系统才有条件跨越分叉集，进而导致溶洞顶板失稳，因此u>0是岩溶区嵌岩桩溶洞顶板稳定的必要条件，即：

(20)

为安全起见，选取最大水平地应力σhmax作为加载在溶洞两端的水平地应力，整理可得溶洞顶板最小安全厚度要满足：

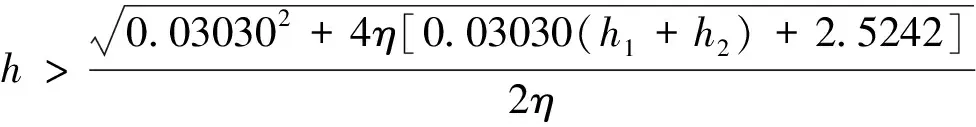
(21)

式中，η可按式(22)计算：

(22)

(2)岩溶区嵌岩桩溶洞顶板稳定的充分条件

根据突变理论，当结构系统满足分叉集方程式(15)时，溶洞顶板必然发生失稳[16]。因此可分别令分叉集方Δ>0，Δ=0，Δ<0对溶洞顶板的稳定性进行讨论。

1)当Δ>0，平衡曲面方程式(14)只有1个实数根，此时系统变形是连续的，系统处于稳定的平衡态，溶洞顶板不会发生突变。

2)当Δ=0，式(14)将有3个实根，其中有2个相等的实根，即：

(23)

式中x1对应不稳定平衡点，x2，x3对应稳定平衡点，当系统受到扰动时发生突变时，必定从一个分支跨越到另一个分支，突变值为：

(24)

此时，系统存在一个极限稳定状态，溶洞顶板处于临界稳定状态。

3)当Δ<0，式(14)有3个不相等的实根，对应3个平衡状态，此时系统跨过分叉集，溶洞顶板将发生失稳。

根据上述分析，岩溶区嵌岩桩溶洞顶板稳定的充分条件是Δ>0，整理后可得：

(25)

式(25)是一个关于溶洞顶板最小安全厚度h的超越方程，可通过数值方法进行求解。

综上所述，岩溶区嵌岩桩溶洞顶板最小安全厚度的充要条件为式(21)和式(25)。

2.5 安全储备的讨论

由于岩溶区嵌岩桩溶洞顶板的安全厚度受到诸多因素的影响，如岩石节理裂隙发育、溶洞地下水情况、溶洞自身形态等，且由于对顶板计算模型进行了相应的简化，如假定了桩端阻力为集中力作用在顶板上等，与实际情况存在着差异。因此，工程中一般采用安全系数的方法，建议安全系数k一般取3.0～4.0[17]。

3 工程算例

某高速公路一座跨越岩溶区的桥梁，本文选取其0#桥台的1根桩进行验算，其基本工程概况如图4所示，该桩作用在圆柱形溶洞正上方，计算参数取值如表1所示。

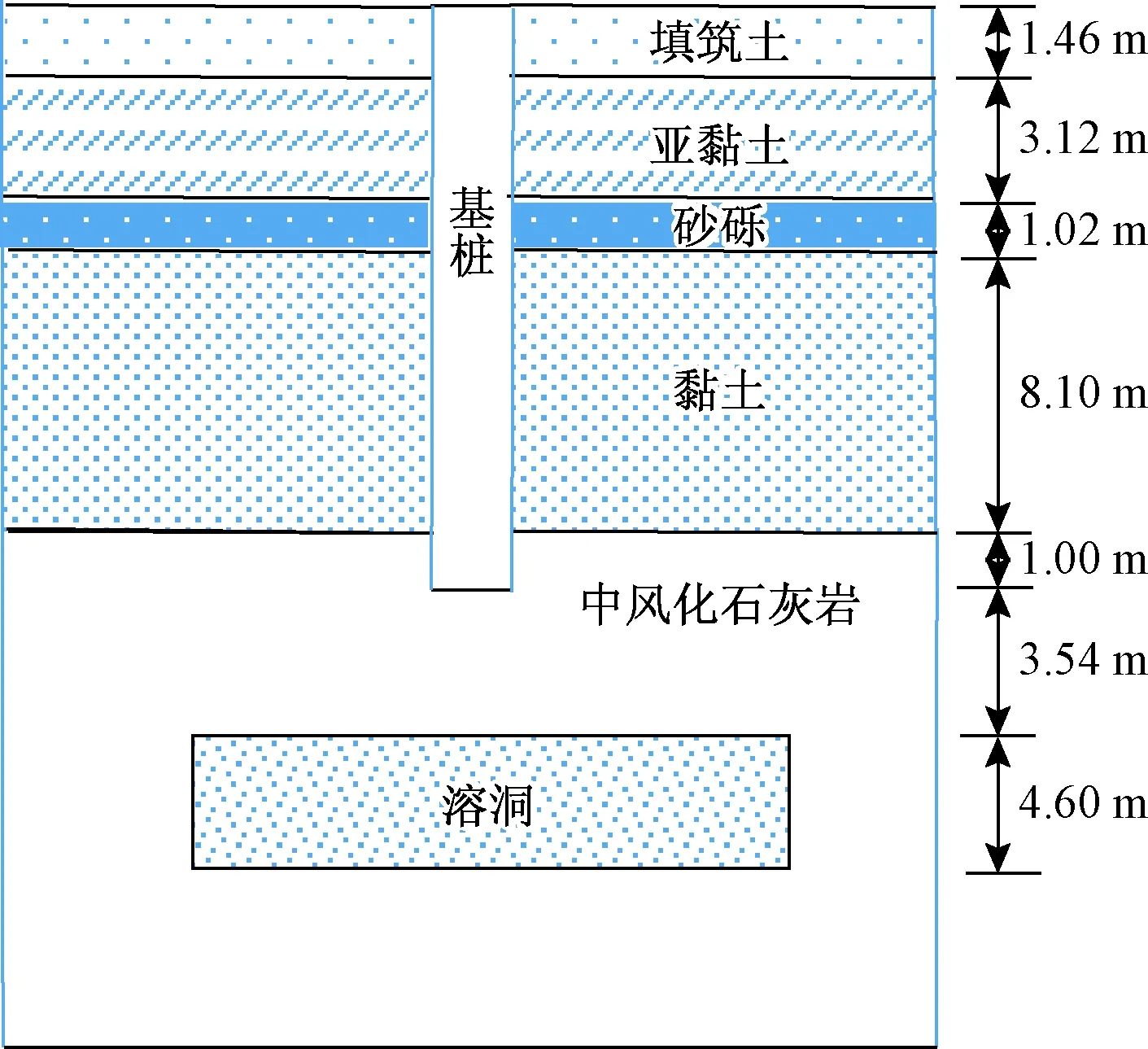
图4 工程概况Fig.4 Engineering overview

计算参数取值桩长l/m14.7嵌岩深度h/m1桩径d/m1.5溶洞跨径L/m18设计荷载F/kN9 186中风化石灰岩弹性模量E/GPa17中风化石灰岩泊松比μ0.25中风化石灰岩重度γ/( kN·m-3)28填筑土重度γ1/( kN·m-3)17亚黏土、黏土重度γ1/( kN·m-3)18砂砾重度γ1/( kN·m-3)20

结合上述工程，采用本文的方法，安全系数k取4.0。根据岩溶区嵌岩桩溶洞顶板最小安全厚度的必要条件，按式(21)计算可得溶洞顶板的最小安全厚度为h=3.02 m，将求得的顶板最小安全厚度代入式(15)中可得分叉集方程Δ>0，即溶洞顶板稳定的充分条件满足要求。

为进一步验证该方法的可靠性，将本文计算与按梁板理论计算的结果进行对比。按照文献[17]中的计算方法，安全系数k仍取4.0，当溶洞顶板按抗冲切进行验算时，可得溶洞顶板的最小安全厚度h=9.72 m；当溶洞顶板按抗剪切进行验算时，可得溶洞顶板的最小安全厚度h=2.04 m；当溶洞顶板按弯拉进行验算时，可得溶洞顶板的最小安全厚度h=6.83 m。可见，按照传统梁板理论计算求得的顶板最小安全厚度变化范围较大，若取顶板分别按抗冲切、抗剪切、抗弯验算求得的最小安全厚度的最大值h=9.72 m作为工程设计时的安全厚度，计算结果过于保守。

本文计算得到的顶板最小安全厚度h=3.02 m，介于顶板按抗剪切验算与顶板按抗冲切验算所求得最小安全厚度之间。而实际工程中桩端岩层厚度为3.54 m，处于稳定状态，故未对溶洞进行处置，目前该工程运行竣工多年且运行良好，因此本文计算方法在工程设计中是合理可行的。

4 结论

(1)根据岩溶区嵌岩桩-溶洞体系的工程特点，将结构系统简化为顶板两端受滑动支座约束，且水平向作用地应力的平直梁模型，基于尖点突变理论分析顶板失稳破坏机制，为岩溶区嵌岩桩溶洞顶板稳定性的研究提供新的定量分析方法。

(2)根据岩溶区嵌岩桩溶洞顶板稳定的充分条件和必要条件，导得溶洞顶板的最小安全厚度，该方法综合考虑了上覆岩土体自重及桩端荷载对溶洞顶板稳定性的影响，并通过工程实例验证了本文方法的可行性，可为同类工程提供参考。

(3)本文计算方法将溶洞顶板视为平直梁模型，对现有梁板结构进行了优化，但仍未考虑溶洞实际尺寸效应的影响，对尺寸效应的研究将是笔者今后研究的重点。