一种基于稀疏描述的X射线焊缝检测方法

王侦倪，高炜欣,汤 楠

(1.西安石油大学 陕西省油气井测控技术重点实验室，陕西 西安 710065；2.西安石油大学 光电油气测井与检测教育部重点实验室，陕西 西安 710065)

引 言

焊缝检测的方法有很多，其中，基于X射线图像的缺陷检测是目前应用最为广泛的无损检测方法[1]。多数算法都是先提取焊缝图像，根据图像处理的方法判别缺陷图像类型。在已有的研究中，文献[2]使用一种基于水平集[3]的主动轮廓模型 Chan-Vese模型[4]对焊缝缺陷进行分割，这种方法对对比度明显的缺陷图像有较好的判断效果，但不能准确判断不明显的缺陷。文献[5]提出先确定焊缝图像位置，然后利用形态学对焊缝图像进行缺陷检测的方法，提高了判别的准确性。文献[6]指出利用部分缺陷的方法，在观察到存在缺陷的位置采取分水岭变换和子束变换分割出焊缝缺陷。文献[7]在检查较厚的器件时发现器件不能及时同步且存在噪声较大等干扰因素，利用消除法和波形分析法检测出焊缝缺陷。文献[8]在对缺陷类型识别之前，对采集到的图像首先处理模糊边缘，采用了传统的图像分割方法(如边缘检测法和阈值分割法)。文献[9]指出文献[8]提取真实边沿比较困难，基于文献[8]的问题，文献[9]提出基于支持向量机的焊缝缺陷检测方法，这种方法是先对样本进行训练，针对所得模型分割缺陷图像。

从现有的研究可以看出，大多数缺陷识别都要首先将缺陷进行分割，根据分割后缺陷几何或纹理特征判断缺陷的类别。但焊缝图像具有较高的噪声，缺陷对比度较差，清晰度较低，为实现缺陷的准确分割带来困难进而影响到缺陷特征的准确求取。针对以上问题，许多学者提出了很多解决方法。Zapata[10]等人提出一种基于自适应网络的模糊推理系统(ANFIS)。利用缺陷形状与主方向特征等12个几何特征并使用ANFIS进行缺陷分类。Zhao[11]等人对缺陷提取了随机分布三角形特征，并使用稀疏表示分类器(SRC)进行缺陷分类，相比SVM，有更好的识别率。这些方法在一定程度上可以从缺陷图像中检测出缺陷，但这些方法几乎都是对焊缝缺陷图像进行分割，获得阈值判断缺陷类型。因为现场提取的 X射线焊缝图像本身辨别度不高、灰度较为分散，焊缝缺陷边沿不明确，而且由于噪声的干扰，这些都增大了阈值准确分割的难度。为了避免缺陷图像的分割，简化识别过程，提高判别的精确度，本文基于稀疏描述的原理[12]，提出一种缺陷识别的方法，通过模式识别，将现场提取的原始图像分为有、无缺陷图像并作为样本，对待检测图像进行线性组合，通过系数向量分析直接判断缺陷和噪声，避免了特征值计算，达到良好的识别效果。

1 图像分析

现场提取的实际焊缝图像及焊缝整体灰度直方图如图1所示。通常情况下，原始焊缝图像主要存在图像较小和噪声影响两方面的问题。造成这类问题通常有2个原因：第一，检测的焊缝图像是制件的焊缝经过 X射线透视后，在胶卷上感受光产生阴影，转化为数字图像文件后，存在灰度较为聚集、对比度不高且缺陷特征被淹没等问题。第二，处理图像的每一个过程及处理结果都要受到噪声的影响。由图像的灰度直方图可以看出图像是否清晰，由图1可知，完整的焊缝图像灰度直方图偏向于右边一侧，图像较为明亮，且直方图较为集中，说明图像本身对比度不高，存在的缺陷将难以被肉眼识别。基于以上问题，本文引用疑似局部图像的概念，如图2所示为疑似缺陷外切矩形。图3为分割出的SDR及灰度直方图，该直方图相比于图1灰度匀称分布，图像清晰，易于判断。本文采用模式识别的方法，通过研究模板图像，根据“疑似局部图像”判别，增大了判断的准确率，避免了缺陷图像的准确分割和特征值的计算。

图1 X射线焊缝图像及灰度直方图Fig.1 X-ray weld image and grayscale histogram

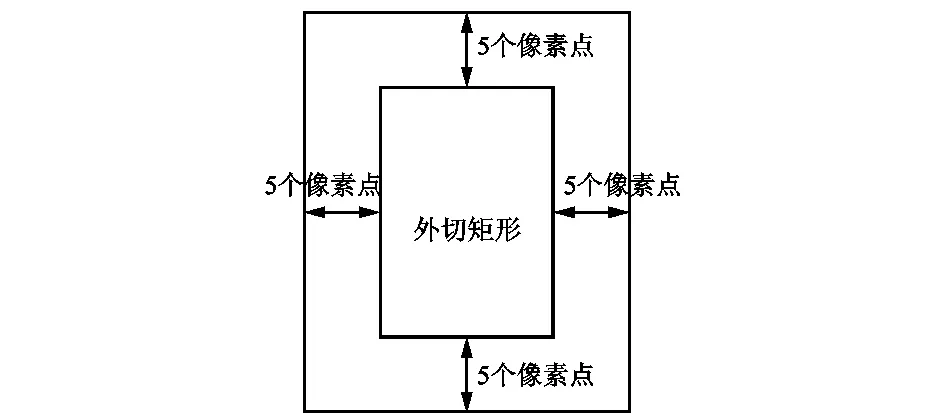
图2 疑似局部图像定义Fig.2 Suspected local image definition

图3 缺陷图像及灰度直方图Fig.3 Defect image and grayscale histogram

2 稀疏描述原理

基于小波分析理论，Mallat 和 Zhang 在1993年首次解释了信号在过完备基上分解的构想[13]。在现场提取未经处理的图像数据较大，而将图像进行稀疏表示能够压缩图像，加快计算过程，所以在图像处理领域得到了广泛应用。

图像信号主要包括两种稀疏模型(合成稀疏模型和分析稀疏模型)，本文中图像信号模型为合成稀疏模型，这种模型是指对于给定的一组信号都可以在过完备字典的基元张成的空间下表示，其系数只有少数的非零元素，大部分系数值都相对较小，接近为零，这样可以认为信号在该字典下能够稀疏表示。未经处理的自然信号一般情况下在时域内都是非稀疏的，数据量大，增加了图像处理的难度，但是这些信号可以通过某些变换域成为稀疏信号，通过稀疏表示原始图像的信息，降低了计算的难度。由调和理论可知，用向量f表示一维离散时间信号，它的长度为N，用一组标准正交基的线性组合可以表示f：

(1)

3 问题描述

图像识别是先将训练样本进行k类标记，将采集到的原始图像与训练样本比对，然后判断待检图像是否符合样本的所属类型。设待检测图像和样本图像的分辨率为h×w，将每幅图像的像素点按照列优先的原则变换成为一个列向量f∈Rm，m=h×w，那么n个训练图像组成字典矩阵(也称基矩阵)

A=[f1,f2,…fn] ∈Rm×n。

在压缩传感理论中，矩阵A被称为字典矩阵。假定字典矩阵A对应的合成矩阵为ψ，则超完备稀疏表示就是从所有表示中找出分解系数最为稀疏的一个，即：

(2)

在稀疏表示的框架下，当有足够多的样本图像时，焊缝图可由样本图像线性组合。设y为待检测图像，则将y表示为

y=a1f1+a2f2+…+anfn。

(3)

其中，ai∈R为实系数。

本文从数据库中采集了部分管道焊缝的SDR图像，将图像分类为圆形缺陷样本、线形缺陷样本和噪声样本，如图4所示。从图4可以看出，X射线检测出的焊缝图像无论缺陷或是噪声都具有一定的相似性。本文将样本图像进行分类排列，分为“正常”和“缺陷”两类。设“正常”图像有k个，“缺陷”图像有n-k个，则将A向量按照下式重新排列。

A={f1,f2,…fk，fk+1,…fn}。

(4)

该分解过程借助字典A，对于一组给定的图像向量化信号y，考虑其为字典A中少数基元的线性组合，其线性方程为：

y=A·x。

(5)

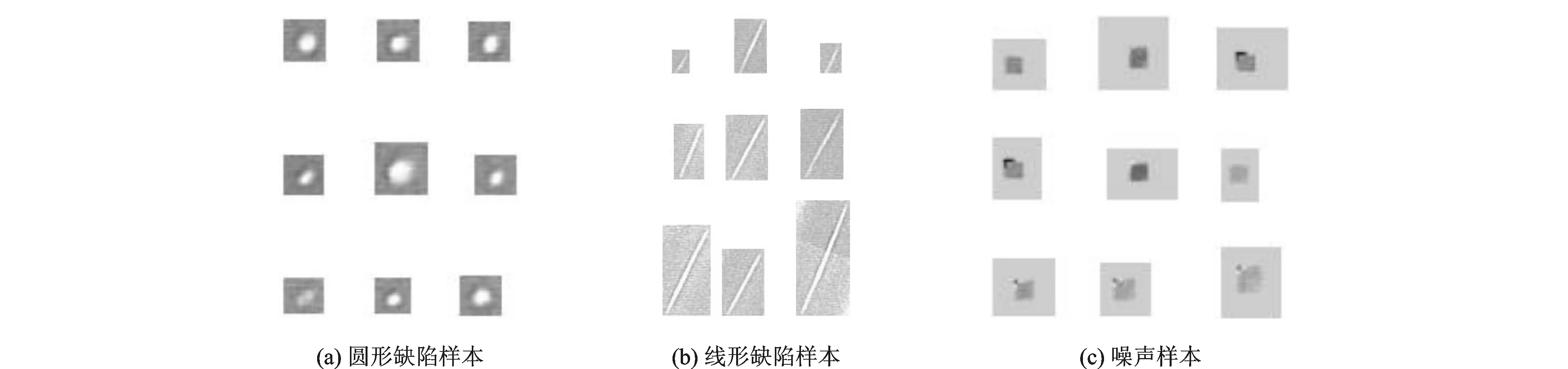
图4 缺陷及噪声样本Fig.4 Defect and noise samples

4 字典矩阵模型

为了获取较好的重建结果，本文提出了通过学习获得字典矩阵实现优化。在基于过完备稀疏表示的图像处理中，删除相关性较大的SDR图像，由某种特定字典稀疏表示特定种类的SDR图像。利用字典矩阵向量的相关性，即通过求解

(6)

构建焊缝缺陷字典矩阵学习模型。式中，ψi为字典矩阵ψ第i列元素。式(6)的求解式目标是通过求解各列的相关性，以相关性最小为原则构造字典矩阵模型。

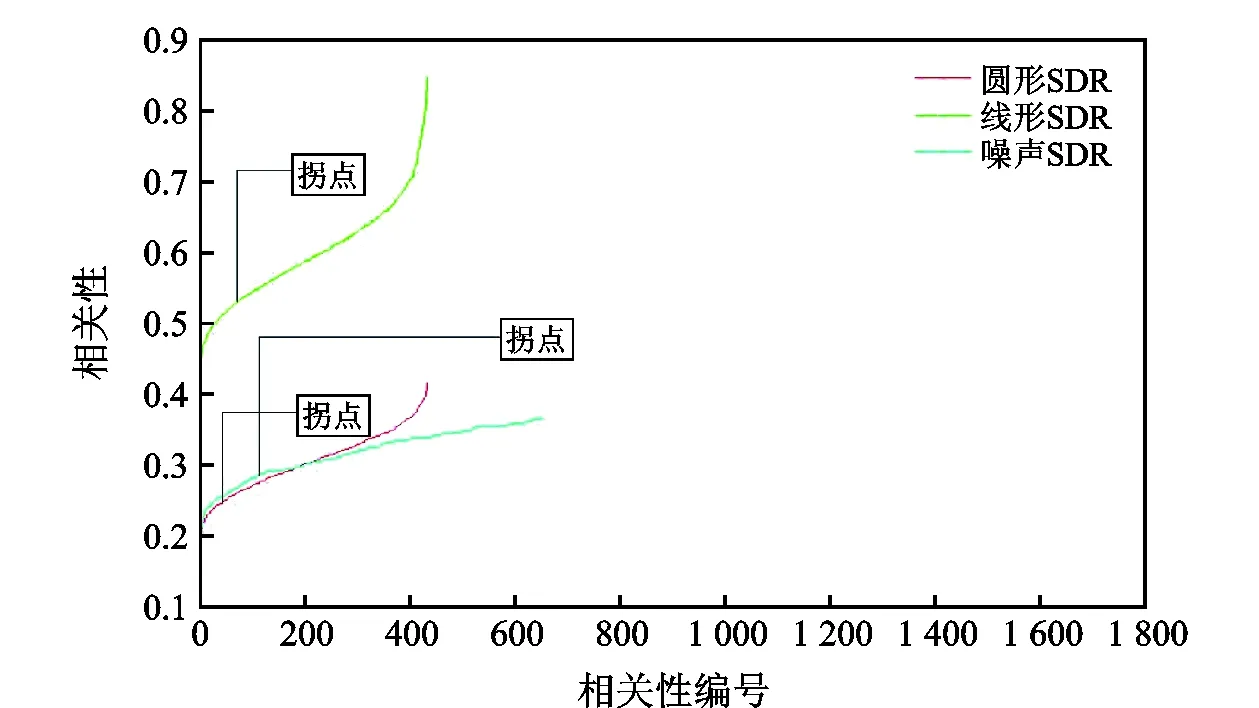
图5 SDR相关性统计曲线Fig.5 SDR correlation statistic curve

由图5拐点位置可知，总样本数量在40～100之间即可满足要求。本文提出利用贪心算法确定最佳的样本数量及对应的字典矩阵。即通过求解式(6)完成样本选择。

贪心求解策略描述如下：

(1)将每个圆形SDR、线形SDR、噪声SDR依次扫描，将图像的像素点按照列优先的原则逐个变换成一个列向量，最后生成3个样本矩阵;

(3)首先选取相关性最小的两列为局部最优解，然后由小到大依次选取，重复此过程，删除重复选取列，直到满足最优样本数量组成全局最优解，算法结束。

5 算法实现

若将大部分的信号进行变换，则信号可以稀疏表示，所以为了得到信号y在A上的稀疏系数向量，求解该问题可以化为零范数最小化问题。即有

(7)

零范数问题可以看成是线性规划问题，近期的研究理论表明只要信号是稀疏的，可以采用凸-凹优化技术实现对优化问题的求解，即可以通过求解凸优化问题准确地表示信号。零范数最小化问题是非凸问题，很难求解，因此本文引入如下g(x)函数：

(8)

其中Δ为归一化系数。式(8)的曲线如图6所示。

由于凸优化的良好性能，所以判断函数是否为凸函数成为解决优化问题的关键。通过计算可知，g(x)为下凸函数。

判定算法的流程图如图7所示。

图6 g(x)函数值Fig.6 g(x) function

图7 g(x)判定算法的过程流程Fig.7 Process of g(x) decision algorithm

g(x)为光滑连续函数，可以求导。因此，可以通过引入g(x)，将式(7)转化为

(9)

其中，K为惩罚项系数，求解式(9)可以方便地获得系数向量。

采用最速下降法求解式(9)，步骤如下：

Step1： 选取初始点x0∈Rn，允许误差0<ε<1,令迭代次数p=200。

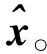
Step3：令αp=0.000 1，计算xp+1=xp+αpdp，转Step2。

6 实验分析

6.1 实验模型

实验从数据库一共选取缺陷SDR和噪声SDR各60张，再另选100张真实缺陷和100张噪声SDR作为待检测图像,如图8所示。首先将样本图像转化为灰度图，由于图像大小不一样，实验通过选择不同的归一化尺寸将图像大小统一化，然后采用列首尾相接方式把每副图像重排为列向量，再将所有列向量组合为样本矩阵A，按上述方法待检测图像组成列向量。本文与传统算法不同，直接研究样本图像判断缺陷。

在进行实验前，首先建立混淆矩阵，格式见表1。

图8 100组缺陷图像和100组噪声图像Fig.8 Images of 100 groups of defects and noise

检测为有缺陷检测为无缺陷存在缺陷图片(真正,true positive,TP)(假负,false negative,FN)未存在缺陷图片(假正,false positive,FP)(真负,true negative,TN)

由混淆矩阵得出敏感度和特异度公式如下：

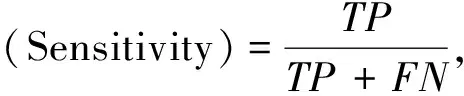
(10)

(11)

由于噪声图像和缺陷图像的大小不同，不能直接运用到求解过程。而且图像的大小影响缺陷特征的清晰度、对比度，当尺寸选择较小时，图像特征不明显，尺寸选择较大会导致缺陷边缘模糊，选择合适的尺寸对提高焊缝缺陷识别的准确率具有重要意义。因而在对焊缝缺陷图像进行检测与识别之前，对图像大小归一化是必不可少的步骤。图9为经过不同的归一化的图像对比。实验首先研究了取不同归一化图像尺寸对识别结果的影响，然后在分析尺寸影响的基础上，选择最优尺寸建立样本矩阵与测试矩阵完成识别过程。其次选取不同的惩罚项系数K，在分析其对识别结果的影响的基础上，确定最优系数。综上，可以通过减少样本数量，简化计算过程，在确定最优尺寸及最优系数后，分析不同的样本数量对分类准确性的影响。

图9 样本归一化图像Fig.9 Normalized images of sample

6.2 实验结果

(1) 尺度归一化影响

实验选取了5组尺寸数据对图像归一化，所得的混淆矩阵如表2所示。由表选取20*20是最佳归一化尺寸。

表2 归一化计算结果Tab.2 Normalized calculation result

(2)惩罚项系数K的影响

实验确定归一化大小为20*20，随机选取5组惩罚系数，判断惩罚系数的大小是否会对缺陷的识别产生影响。识别准确率见表3。

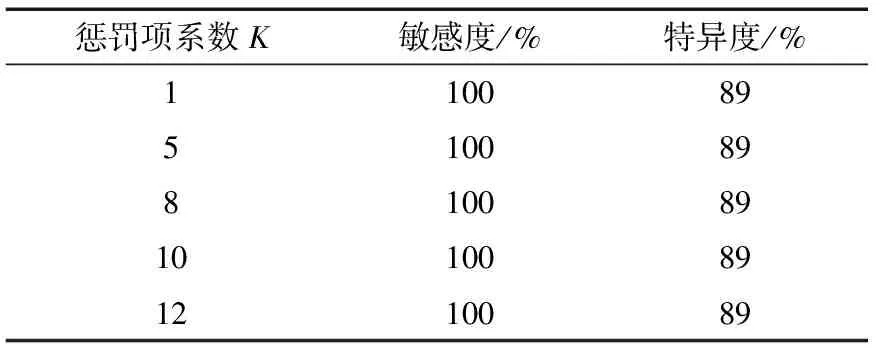
表3 K值计算结果Tab.3 Calculation results of K

由表3可见，惩罚项系数对焊缝缺陷识别的准确率没有影响。

(3)样本数量的影响

根据上述实验结果，本文将SDR归一化为20*20的模板，确定惩罚项系数K=5。在原有的样本的基础上，通过贪心算法把样本数量分别减少为40,60,80，100,识别效果见表4。

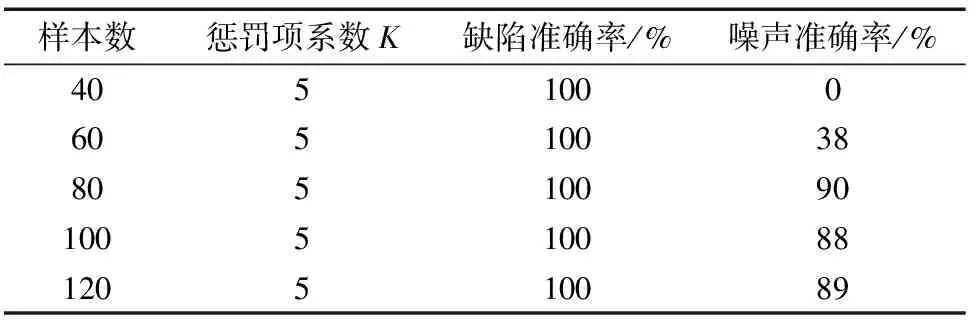
表4 样本数计算结果Tab.4 Sample number calculation result

由表4可知，当选择样本总数为80，即包括20张圆形缺陷，20张线形缺陷，40张噪声SDR时，识别准确率达到最高。所以减少样本数量不仅能够简化算法，还能提高判断的准确率。故本文最终选用80张SDR构成字典矩阵。

7 结 论

本文提出了基于稀疏描述的焊缝缺陷识别的方法，首先通过压缩感知传感技术对图像进行处理，采用罚函数法求解零范数，求解结果为一组系数，分析系数组合判断缺陷。相比于其他识别方法而言，避免了特征值的计算，通过贪心算法选取最优样本数量既简化了计算过程，又提高了识别的准确性。