利用近似马尔科夫毯的最大相关最小冗余特征选择算法

张俐,王枞,郭文明

(北京邮电大学可信分布式计算与服务教育部重点实验室,100876,北京)

近年来,基于互信息的特征选择算法受到国内外学者的广泛关注[1]。Zhang等仅考虑特征与类别标签之间的相关性,而忽视了无关特征或者冗余特征[2];FCBF算法[3-4]采用对称不确定性原则作为特征与类别标签之间相关性判断的准则,但是这样所得子集并不是最优子集;mRMR算法[5-6]采用最大相关最小冗余的准则进行特征子集的排序,使用包装方法进行特征子集的选择,它的问题是特征子集计算时间长,不能有效删除冗余特征。这些不相关和冗余特征往往会降低模型的预测准确性和算法学习效率[7]。因此,非常有必要在数据预处理阶段,对这些不相关和冗余特征进行降维处理[8]。通过降维处理既可以有效降低特征维度,又可以防止模型出现过拟合现象,进而提高算法的精确度。

针对上述问题,本文提出基于近似马尔科夫毯的最大相关最小冗余特征选择(nmRMR)算法,该算法包括特征相关性排序和冗余特征删除两个阶段:第1阶段,利用最大相关最小冗余准则进行相关特征排序,并采用前向迭代搜索方法进行最优特征的选择;第2阶段,采用近似马尔科夫毯算法删除冗余特征和不相关特征。

1 互信息、mRMR准则与马尔科夫毯条件

定义1设一个随机变量Y有D个维度,Y=(y1,…,yD),根据香农的信息论[9],一个随机变量Y的不确定性可以通过熵H(Y)来度量,同理,对于两个随机变量X和Y,它们之间的条件熵H(X|Y)表示为当Y确定时,对X的不确定性的度量。I(X;Y)是随机变量X中包含的关于另一个随机变量Y的信息量。因此,I(X;Y)、H(X|Y)和H(X)三者之间的关系为

I(X;Y)=I(Y;X)=H(X)-H(X|Y)=

(1)

式中:p(x)和p(y)分别为随机变量X和Y的概率密度,p(x,y)为联合概率密度。

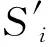
定义3特征与标签之间的相关性。假设S为特征集合,|S|为特征数;C为标签。I(fi;C)为特征fi与标签C之间的互信息,如果S中存在1,2,3,…,n个特征,I(fi;C)的互信息最大,那么,特征fi表示S集合中最强相关特征,依照mRMR算法的最大相关准则,是选出满足如下等式的特征的方法

(2)

定义4特征间的冗余性。假设F为特征全集,S⊂F,fi∈F-S,fj∈S(i≠j),则I(fi;fj)为特征fi和特征fj之间的互信息。mRMR算法最小冗余准则满足

(3)

定义5根据mRMR算法[7]特征与标签相关性最大、特征间冗余性最小的原则,可得到mRMR算法的计算式

(4)

定义6马尔科夫毯描述[10]。S⊂F,fi∉S,fi的马尔科夫毯的条件是fi⊥{F-S-{fi},C}|S,其中⊥表示独立,|S表示以S为条件。在给定S集合中,fi独立F-S-{fi}和C,这说明,当S集合存在时,fi对于标签C已经没有任何贡献了,应该立即删除。同时,也说明满足上述条件的最小特征S集合为特征fi的马尔科夫毯。

定义7近似马尔科夫毯[11]的判断条件。对于特征fi和特征fj(i≠j),特征fi是特征fj的马尔科夫毯条件为

(5)

2 nmRMR算法描述

本文提出nmRMR算法,具体步骤如下:

步骤1初始化F、S集合并设置S集合为空集合;

步骤2计算F集合中每一个特征与标签之间的互信息,按照互信息大小对F集合中的特征进行降序排序;

步骤3将F集合中的第一个特征fi存入S集合,将fi特征从F集合中删除;

步骤4按照最大相关最小冗余准则进行特征之间的排序操作,将排序好的特征存入S集合中;

步骤5按照近似马尔科夫毯条件判断,在S集合中进行不相关特征和冗余特征删除操作;

步骤6输出最优的特征集合,即S集合。

3 实验结果与分析

3.1 nmRMR算法实验

本文的实验环境是Intel(R)-Core(TM)i7-500U,内存是8 GB,Windows7-64 bit操作系统,仿真软件是python3.6和Jupyter Notebook。数据统计分析软件是IBM SPSS Statistics20。

实验数据集选择了国际著名的UCI通用数据集,数据集涉及医学、工程科学和生物科学等领域,8个样本数据集包含不同的样本数、特征数和类别数,数据集的具体参数描述见表1。样本数的范围为27～4 601,特征数的范围为23～91,类别数的范围为2～17。

表1 实验测试数据集的描述

由于某些数据集中具体特征值存在缺失导致样本不完整,在进行实验前,直接删除不完整的样本,根据Kuargan提出的类别属性依赖最大化方法[12]离散化处理连续型数据。

本文采用预测分类准确率最为常见的k-NearestNeighbor分类器(简称为KNN)[2]和Native Bayes分类器[13-15]来构建预测模型。

3.2 分类结果实验分析

在实验过程中采用10折交叉验证方法进行实验,10折交叉验证就是每次将数据集平均分成10等份,其中9份作为训练数据集,1份作为测试数据集。为了保证公平,每个数据集都做10次实验,通过10次结果求平均值来求得平均准确率。与FCBF、mRMR和Fullset算法进行对比,验证本文算法是否可以提高分类的准确率和降低数据的特征数。

比较不同算法优劣性的方式就是两种分类器在8个数据集上进行验证。FullSet算法不进行任何特征排序;mRMR算法依赖于最大相关最小冗余准则进行特征排序;FCBF算法和nmRMR算法都是在特征初选时对特征进行排序筛选。FullSet和mRMR算法并不具有特征初选的功能。为了保证本实验的公正性,模拟实验都对初选的特征子集不加以限制。

表2～5分别给出了4种算法在KNN、Native Bayes两种分类器中的分类准确率和选择出特征数比较。由表2可以看出,在spambase数据集中,nmRMR算法分类准确率略低于mRMR算法,但是在其他7个数据集上,nmRMR算法均优于mRMR算法。同时,nmRMR算法的平均分类准确率比mRMR算法提高了0.42%。由表3可以看出,nmRMR算法选择出的平均特征子集数比mRMR算法少了5.375个。由表4可以看出,nmRMR算法和mRMR算法在lung-cancer数据集上平均分类准确率相等外,在其他7个数据集上,nmRMR算法均优于mRMR算法。同时,nmRMR算法的平均分类准确率比mRMR算法提高了1.14%。由表5可以看出,nmRMR算法选择出的平均特征子集数比mRMR算法少了8.375个。由表2和表3可以看出,nmRMR算法的平均分类准确率比FCBF算法提高了0.4%,nmRMR算法选择出的平均特征子集数比FCBF算法少了1个。由表4和表5可以看出,nmRMR算法的平均分类准确率比FCBF算法提高了1.25%,nmRMR算法选择出的平均特征子集数比FCBF算法少了5.375个。

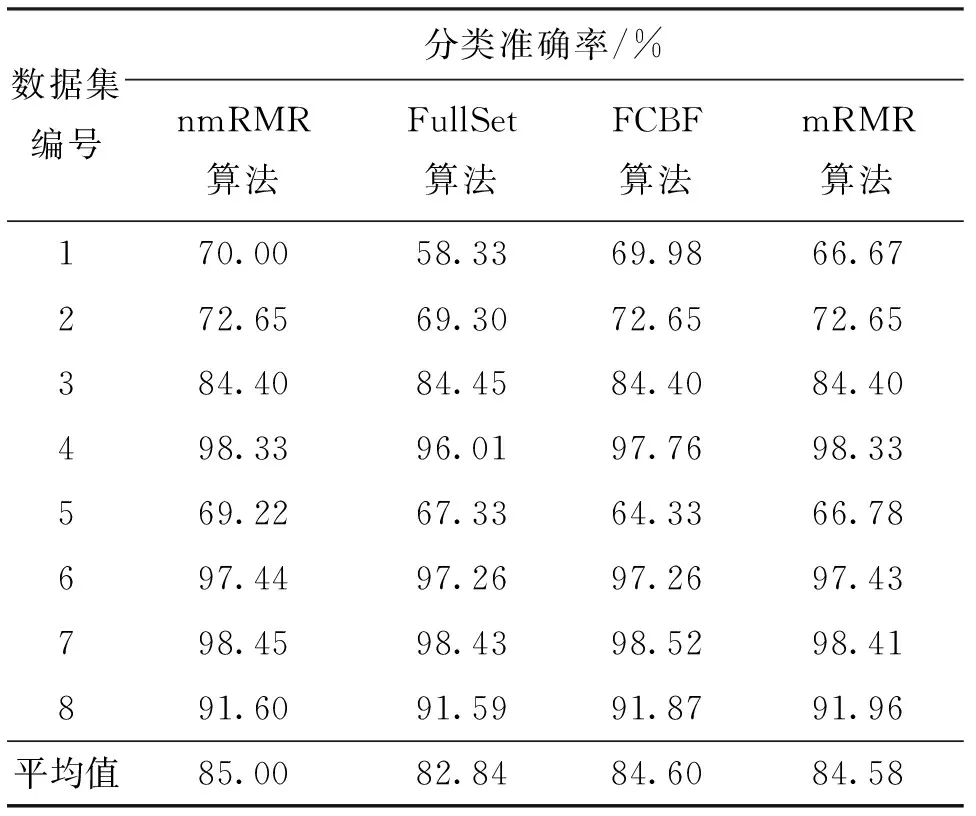
表2 4种算法在KNN分类器中分类准确率的比较

表3 4种算法在KNN分类器中选择特征数的比较

表4 4种算法在Native Bayes分类器中

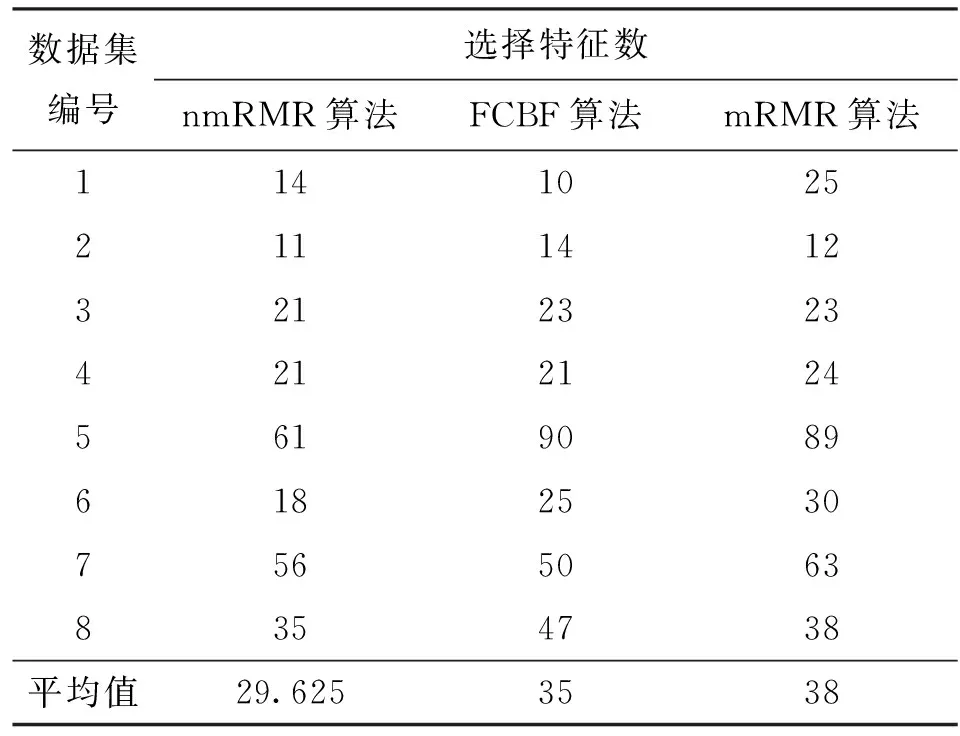
表5 4种算法在Native Bayes分类器中选择特征数的比较

本实验同时给出4种算法在不同分类器上的分类准确率,具体如图1～图4所示。从图1～图4可以看出,nmRMR算法的分类准确率和特征子集的选择均优于或等于mRMR、FCBF和FullSet算法。

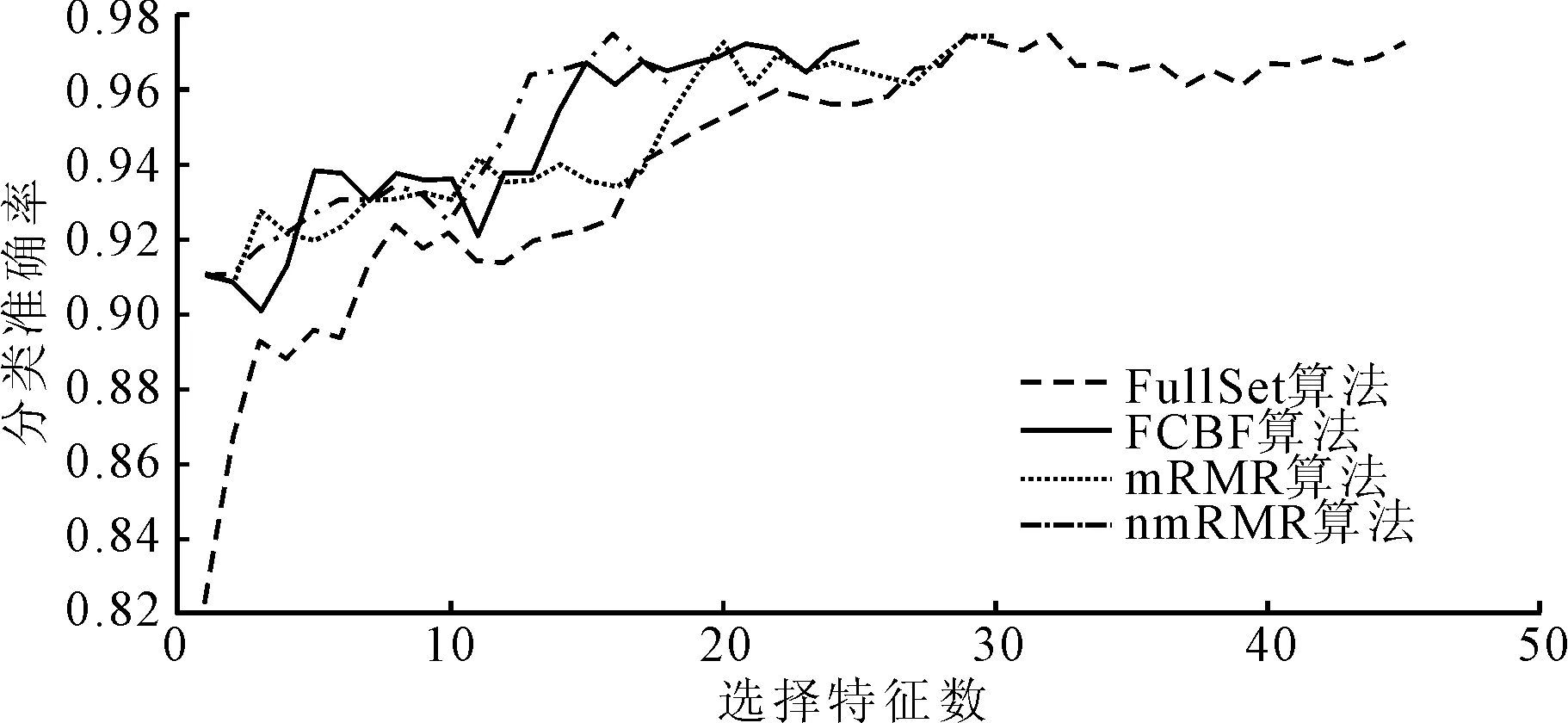
图1 4种算法在KNN分类器中wdbc数据集上 的分类准确率

图2 4种算法在KNN分类器中movement_libras数据集 上的分类准确率

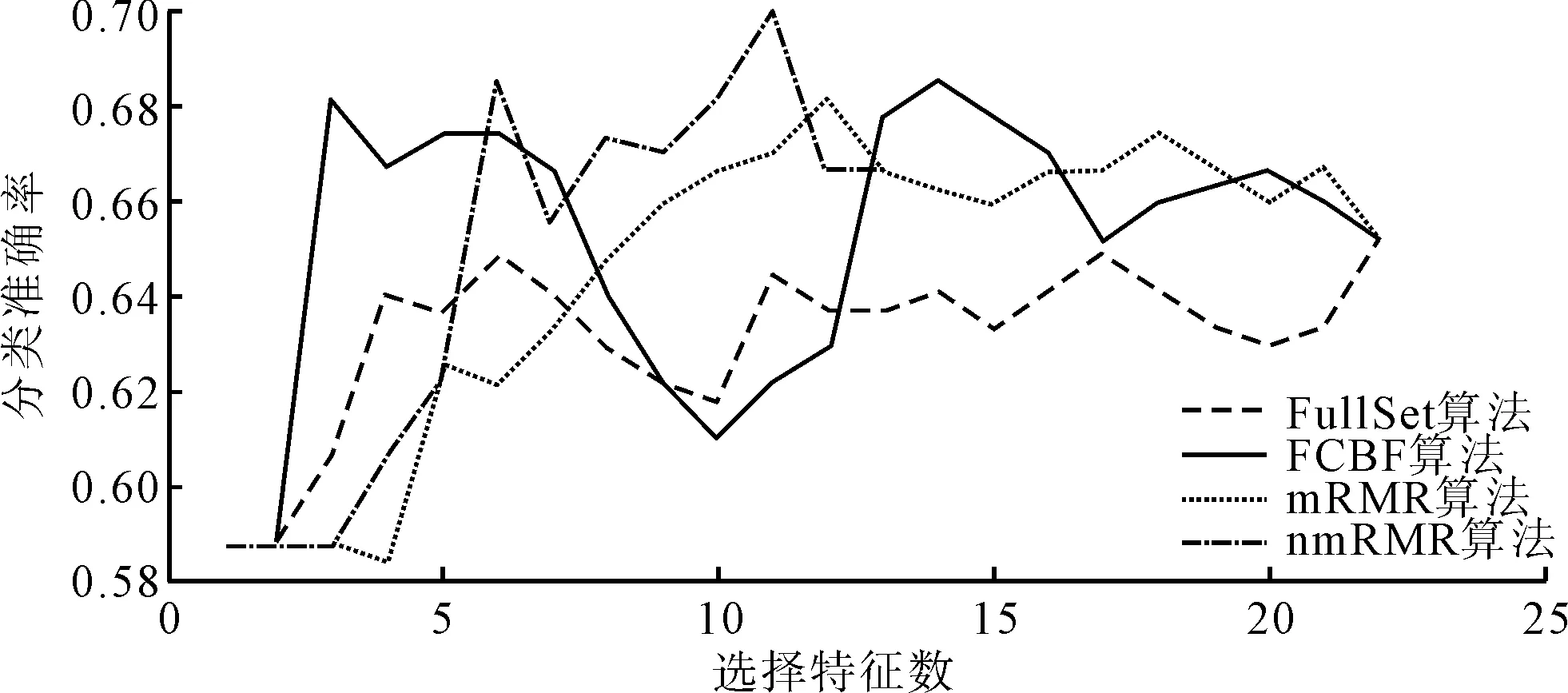
图3 4种算法在Native Bayes分类器中spect数据集 上的分类准确率

图4 4种算法在Native Bayes分类器中ionosphere 数据集上的分类准确率

4 结 论

本文提出了一种基于近似马尔科夫毯的nmRMR特征选择算法,该算法在第1`阶段采用最大相关最小冗余的评价准则进行特征相关性冗余性的分析与排序;第2阶段采用近似马尔科夫毯方法进行特征与标签以及特征间依赖关系的分析,将特征间相互依赖程度高的特征进行删除,保留能够有较高区分能力的特征,组成最优特征子集。由于nmRMR算法具有初期特征子集优选能力,它可以进一步地提高分类学习算法的泛化能力。