一种混合的机动群目标分离检测跟踪算法

杜明洋,毕大平,王树亮,潘继飞

(国防科技大学电子对抗学院,230037,合肥)

密集多目标跟踪是信息融合、航空航天领域的难点问题。尤其是对于空间位置很近、互相遮挡现象严重的目标,如低空飞行的飞机编队、鸟群等。在跟踪上述类型的目标时,可能存在一个雷达波束内有多个目标的情况,从而导致无法分辨出每一个个体目标[1-2]。针对上述问题,相关学者提出对群的整体进行跟踪,主要包括概率假设密度(PHD)滤波和Bayesian递推算法。其中,洛克希德公司提出的PHD滤波算法可以有效跟踪未知数目的空间临近目标,不需要数据关联即可从目标状态中同时提取目标数量和状态估计[3-6],但该算法存在大量的集合积分,推导复杂,并且无法给出目标航迹,不利于实际应用推广[7-9]。Koch提出利用随机矩阵(RM)描述群的形状以改善跟踪效果,将目标形状参数描述为逆Wishart分布,将目标运动状态参数描述为Gaussian分布,采用Bayesian递推的方法对上述参数进行估计[10-15]。

以飞机编队为例,在运动过程中,基于特定的战术要求,会出现分离、合并等机动模式[7],与转弯机动不同的是,成员的合并与分离对于群目标跟踪来说,会引起群形状和质心的明显变化,造成跟踪误差变大。对分离后的群目标仍采用一个椭圆描述群外形显然是不准确的,因为此时单个椭圆将无法反映群的态势[16-17]。文献[16]通过分析椭圆(体)与正定矩阵的关系,提出了一种新的描述群外形的方法,该算法降低了群机动对跟踪精度的影响,但该算法采用半正定规划估计椭圆的半轴,需要大量的迭代寻优计算,从而严重影响了跟踪的实时性。本文基于文献[16]的思想,结合群分离的特性,通过传统随机矩阵算法估计椭圆的尺寸变化检测群的分离,当检测到群分离后,采用k-均值算法对有效量测进行聚类,形成若干个小群,再利用最小二乘法将各分群拟合成椭圆以描述群的形状,最后进行航迹关联。相比前述算法,本文混合算法既提高了对机动群目标的跟踪精度,又提高了实时性。

1 基于随机矩阵的群目标跟踪

1.1 模型建立

(1)运动模型选取当前统计(CS)模型,其运动状态模型为

(1)

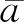
CS模型可以实现闭环的自适应跟踪,但仍存在一些不足之处:首先,CS模型难以根据不同类型的机动自适应地选取自相关时间常数;其次,该模型对于加速度较小的弱机动目标跟踪误差较大。

(2)形态演化模型。该模型描述了目标的形态随着时间的演化过程,包括大小、形状和朝向等方面。文献[14-15]给出了可精确刻画上述过程的演化模型

(2)

式中:p[Xk|Xk-1]为Xk-1到Xk的变化概率;δk为演化分布的自由度;Ak为形态演化矩阵;W(Y;a,C)表示威沙特(Wishart)分布。

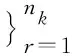
(3)

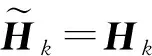
1.2 跟踪算法

状态xk和形态Xk的联合后验概率密度可以分解为

p[xk,Xk|Zk]=p[xk|Xk,Zk]p[Xk|Zk]

(4)

式中:Zk为1～k时刻所有的量测数据。

在随机矩阵的框架下,假设

p[xk-1,Xk-1|Zk-1]=

p[xk-1|Xk-1,Zk-1]p[Xk-1|Zk-1]=

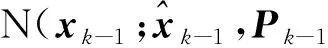
(5)

式中:WI(·)表示逆威沙特(Inverse Wishart,IW)分布。

(1)预测。将运动状态与扩展状态一步预测的联合概率密度函数进行如下分解

p[xk,Xk|Zk-1]=p[Xk|Zk-1]p[xk|Xk,Zk-1]

(6)

式中

(7)

p[xk|Xk,Zk-1]≈

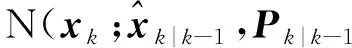
(8)

根据逆威沙特分布的性质,Xk的一步预测的均值为

(9)

(2)更新。给定k时刻数据的个数nk,则有

p[Z(k)|nk,xk,Xk]∝

(10)

将式(8)和式(10)代入式(6),可得

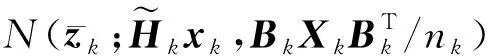
(11)

2 基于聚类的群划分与航迹关联

通过对上节中算法的仿真研究发现,群分离时,基于随机矩阵算法的椭圆估计尺寸变化剧烈,基于此,可以设立门限值η,当连续若干周期,椭圆尺寸变化率均超过η时,即可判为群分离。本文基于k-均值聚类算法,将分离后的群目标分为若干个分群进行跟踪。具体步骤如下。

2.1 群划分

(1)群分离判决。选取椭圆面积的变化率作为群分离的判别指标。当连续γ个周期,椭圆面积的变化率ΔS均高于门限值η,则判为群分离,即

ΔS=π(Δa)(Δb)>η

(12)

(2)选择聚类中心。假设群内聚类数为T,定义群内第t个聚类中心在k时刻的状态向量为

(13)

考虑到聚类中心将参与小群几何中心的计算,因此最好选择群内的目标点,这样可以避免引入新的点迹,影响群内目标的分布。此外,想要选出极有可能不在同一簇的点,一种简单的方法是选择彼此距离尽量远的点迹,即最远原则。基于此,聚类中心的选取按照以下步骤进行:

步骤3分别计算剩余点到前两个聚类中心的距离,两个距离中的较小值作为该点到前两个聚类中心的“得分”,选择“得分”最高对应的点作为第3个聚类中心;

步骤4以此类推,完成聚类中心的初始化。

考虑到基于随机矩阵的群目标跟踪旨在描述群的外形,同时对群的中心进行估计;并且当群内目标较少时,往往对单个目标进行跟踪,单个点目标不存在外形估计问题。因此,分群数量不宜过多,本文中T取2。

(3)形成临时小群。计算群内量测与聚类中心的距离,将量测归于最近的聚类中心,形成t个小群,此时聚类小群不分先后,为临时状态。计算各小群的几何中心为

(14)

(15)

2.2 航迹关联

(16)

选取距离k时刻最近的聚类中心j进行关联,其航迹关联示意图如图1所示。

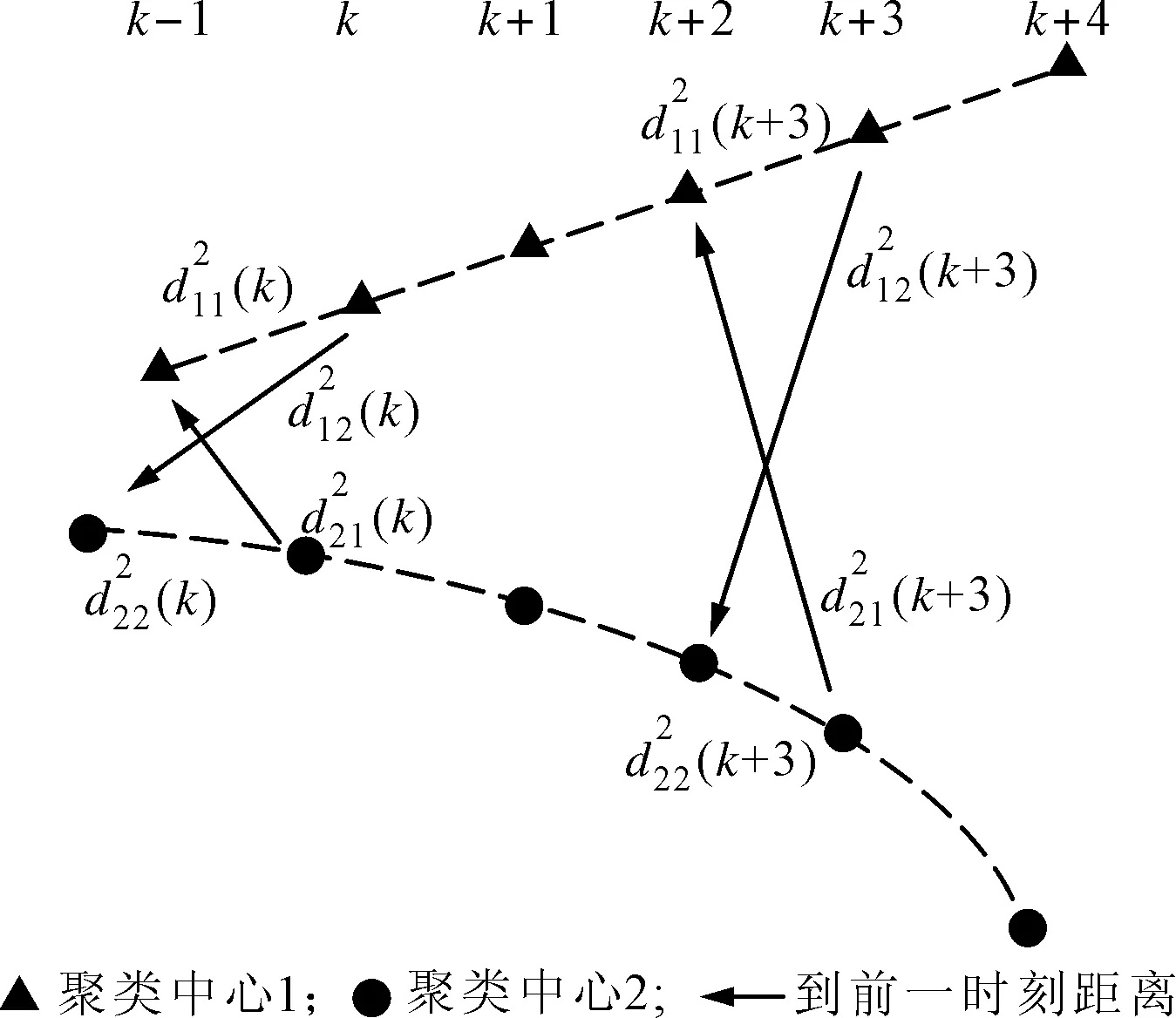
图1 航迹关联示意图

3 基于最小二乘法拟合椭圆

最小二乘法是比较常用的椭圆拟合方法,其思想是在随机误差为正态分布时利用最大似然法进行最优估计,使得测量误差的平方和最小。

D=(X-X′)TWTW(X-X′)

(17)

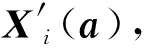
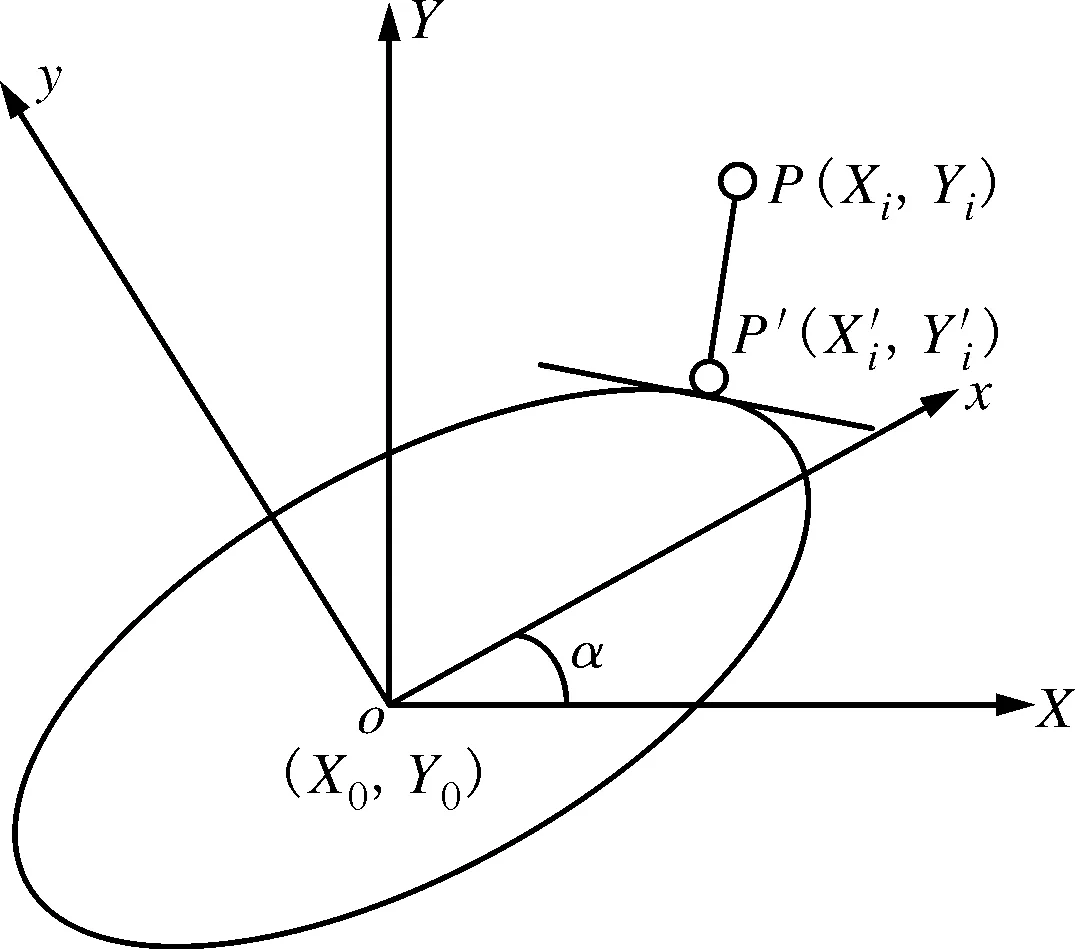
图2 样本点P及椭圆上的正交近邻点P′

(18)

(19)

通过式(19)可得

(20)

式中:J是Jacobian矩阵。

综上,本文算法流程如图3所示。

图3 本文算法流程图

4 仿真结果与分析

本节通过蒙特卡洛仿真实验对本文算法的有效性进行验证。群质心运动状态及形状估计的评价指标采用均方根误差(RMSE),分别定义为

(21)

(22)

4.1 运动场景

跟踪由8个目标组成的群目标,各目标初始位置在(500 m,1 000 m)附近随机产生,目标间距在150～300 m之间,目标在xy平面内运动,模拟实际飞机编队飞行,采样间隔为1 s,仿真运动时间为140 s。群目标运动分为以下6个阶段:

(1)t=1～17 s,vx=200 m/s、vy=50 m/s,匀速;

(2)t=18～43 s,以转弯速率4.77 rad/s左转弯;

(3)t=44～53 s,匀速;

(4)t=54～80 s,以转弯速率-4.77 rad/s右转弯;

(5)t=81～100 s,匀速;

(6)t=101 s时群分离,分群1中包括4个目标继续做匀速运动;分群2中另外4个目标以转弯速率-3 rad/s做右转弯运动。x轴和y轴量测误差的标准差分别为σx=30 m和σy=30 m。检测概率Pd=0.98,门概率Pg=0.999 7,蒙特卡洛仿真次数为50。在滤波过程中产生随机的杂波,杂波的空间位置服从高斯分布,杂波个数服从泊松分布,初始杂波密度λ=4×10-4个/m2。在群分离的判别中,γ选取5,η选取1 000 m2。运动状态估计模型选取“当前”统计模型,其中机动频率设置为α=1/40,amax=50 m/s2,amin=-50 m/s2。群目标外形初始椭圆长短半轴分别取350 m和80 m。

4.2 仿真结果及分析

接收到的量测数据分布如图4所示。为验证本文算法的有效性,分别对二分群和三分群的运动过程进行仿真,并与文献[4]算法进行比较,跟踪及关联效果如图5～图7所示。

图4 量测数据分布

由图5a、5b可以看出,文献[4]算法能够准确地描述群整体发生转弯等整体机动时的外形;但当群分离时,由图5c、5d可以看出,随着群内目标间隔逐渐增大,文献[4]算法对群运动状态和外形的估计误差明显增大,其中外形估计的误差变化更剧烈,这也证明了可以通过群外形估计的变化率判定群是否发生分离。

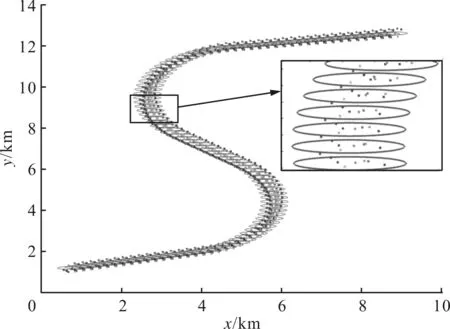
(a)分离前群的外形真实值

(b)分离后群的外形估计值

为验证本文算法中航迹关联的有效性,通过对二分群及三分群的运动过程进行仿真,比较航迹关联前后的跟踪效果,并计算分离前后的跟踪误差,如图6、图7所示。比较图6a、图6b,图7a、图7b,可以看出,本文算法通过计算前后两时刻的各分群间距,基于最近邻思想,较好地实现了航迹关联。比较图6c及图7c、图7d可以看出,本文算法对群分离后的外形估计误差与文献[4]算法对群分离前的外形估计误差是同一量级,证明了算法的有效性。此外,随机矩阵算法估计收敛较慢,并且精度会受到群机动的影响;最小二乘法根据量测值实时地拟合生成椭圆,估计精度不会受到群机动的影响,但依赖于k-均值的聚类结果。

为比较文献[16]、文献[4]与本文算法的精度和实时性,对二分群运动过程进行仿真,计算3种算法的运动状态、外形估计的均方根误差及不同杂波密度下的单次蒙特卡洛耗时,具体结果如图8及表1～表3所示。

(a)未航迹关联

(b)航迹关联

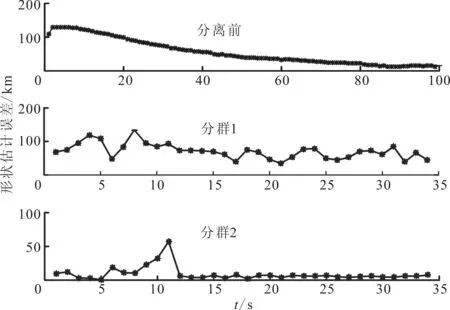
(c)估计误差图6 本文算法跟踪二分群运动场景及性能

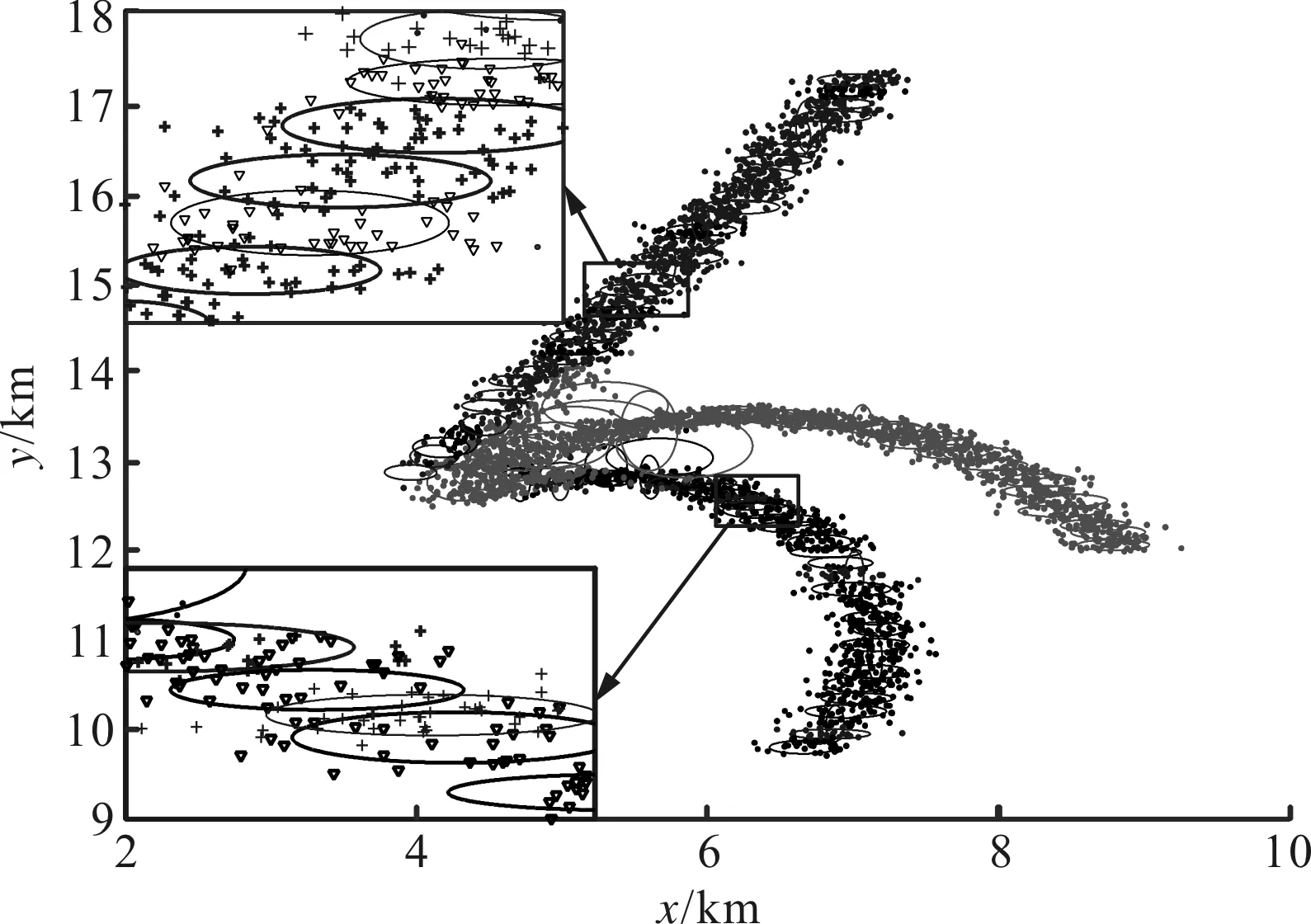
(a)未航迹关联

(b)航迹关联

(c)分离前形状估计误差

(d)分离后分群形状估计误差图7 本文算法跟踪三分群运动场景及性能

图8 2种算法分离前跟踪精度对比

由表3数据可以看出,为了实现对群分离的跟踪,本文提出的混合算法相比文献[4]中单一的随机矩阵算法,单次蒙特卡洛耗时平均增加了35%左右。结合表1、表2中的均方根误差可以看出,文献[16]算法与本文算法对群外形估计的精度相当,但前者耗时较大,影响了跟踪的实时性。这是由于前者采用半正定规划对群外形椭圆的估计过程(包括确定椭圆半轴长上、下界,遍历寻优等)较复杂,大量的迭代运算影响了运算速度,而本文算法基于最小二乘法,在随机误差为正态分布的假设下,只需满足式(20)的各椭圆参数值即可。相比之下,不需要进行迭代和遍历运算,因此实时性更好。

表1 3种算法的运动状态估计均方根误差对比

表2 3种算法的外形估计均方根误差对比

表3 3种算法的算法耗时对比

5 结 论

基于随机矩阵的群目标跟踪算法能够同时估计群质心的运动状态和群的外形特征,逐渐成为群目标跟踪领域研究的热点。针对传统算法对群分离后跟踪误差较大的问题,本文提出了一种基于随机矩阵与最小二乘法相结合的群目标外形估计算法。该混合算法根据传统算法估计椭圆尺寸的变化率检测群的分离,采用k-均值聚类形成分群,最后基于最小二乘法对各分群的外形进行拟合。仿真表明,检测群分离的方法有效,对机动群目标的跟踪精度有明显提高,能够较好地反映群分离后的运动态势及外形特征变化。