离焦对激光通信接收视场的影响分析

许燚赟，董科研，安 岩，朱天元，颜 佳

(1.长春理工大学 光电工程学院，吉林 长春130022;2. 长春理工大学 空间光电技术国家地方联合工程中心，吉林 长春 130022;3. 国家电网吉林省电力有限公司，吉林 长春 130000)

1 引 言

近年来，大气激光通信技术由于具有高速性、保密性及大容量等优势，得到越来越多国内外学者关注、研究及应用。然而，由于通信系统接收视场角的限制，导致对准难度较大，无法达到快速对准通信设备的技术要求[1-5]。

目前，针对对准难度的研究主要集中在两大方面:一是链路性能方面，通过信道编码、增加传输路径及多孔径排布[6-8]等方法，补偿由于对准误差导致的系统通信质量下降，如哈尔滨工业大学的张亚非提出使用调制解调方式和空时编码的方法，以提升通信质量[9]；二是试验装调方面，其通过精确测量对准角度，以达到精确对准[10]。然而，在降低对准难度方面，尚未有文献提出通过离焦增大接收视场角的光学解决方法。对于离焦的研究主要集中在激光制导武器的系统设计[11-13]、离焦光斑偏移对激光通信系统性能影响[14]、离焦比例放大[15]以及像面离焦光斑会聚理论等[16-20]方面。

本文围绕离焦对增大视场的影响展开分析，第二节提出离焦系统模型，导出离焦量与光斑半径的关系；第三节分析了离焦时光斑与探测器位置关系，推导了探测器接收到的光斑能量与视场角、离焦接收能量及离焦量的关系；第四节以探测器接收能量满足通信需求(-35 dBm)为前提，分析并对比了离焦接收能量和离焦量对增大接收视场角的作用。

2 离焦接收系统模型

2.1 光学接收系统像面离焦模型

一般情况下，非成像理想能量聚焦光学系统的半视场角θ表示为

(1)

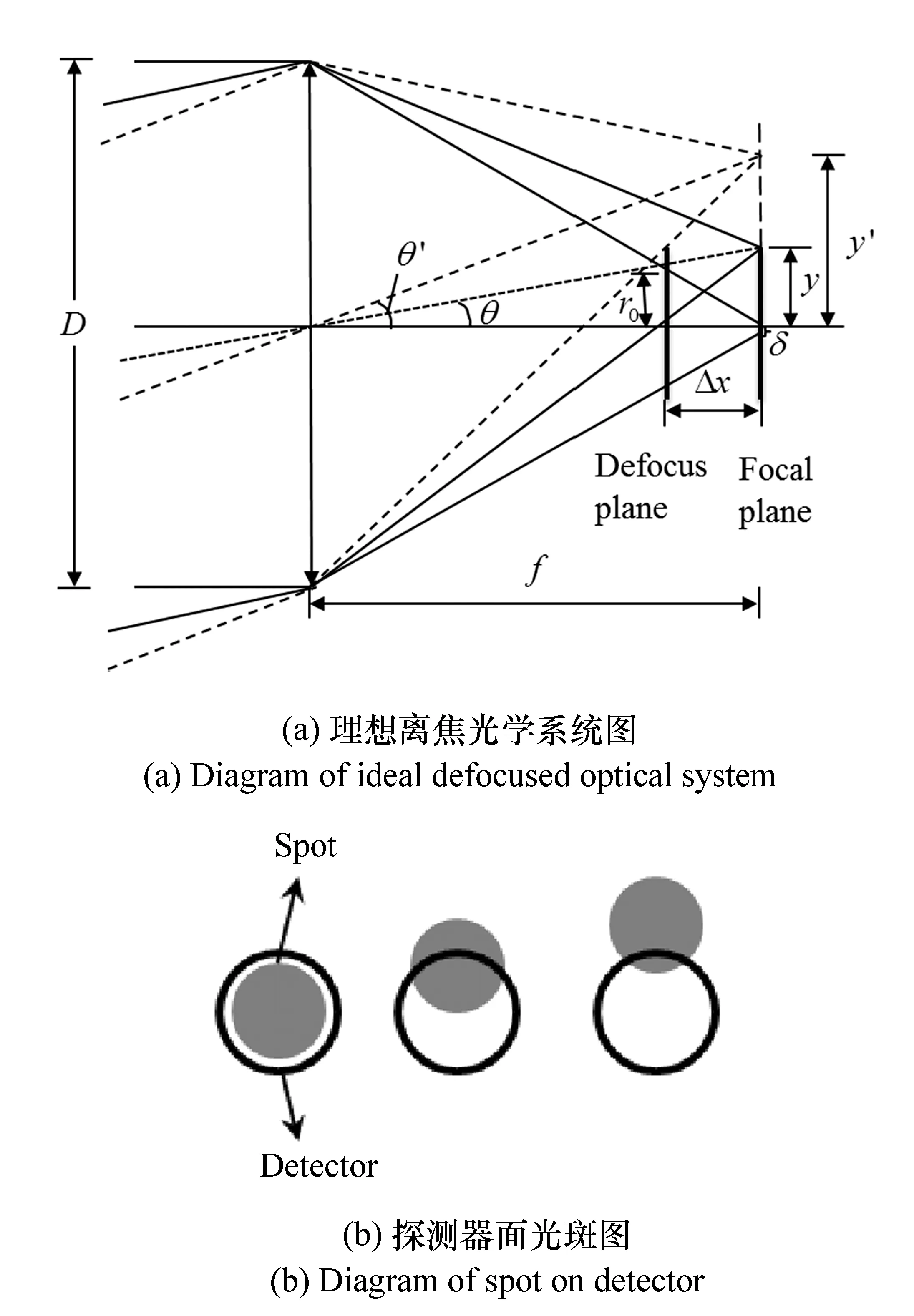
图1 离焦成像模型示意图 Fig.1 Schematic diagram of defocused imaging model

式中，y为理想聚焦系统半像高，f为接收系统焦距。假设系统焦距f固定，当探测器处于焦平面前Δx处，且轴外光线的下边界与探测器面的上边界相交时，探测器恰好不能探测到该临界情况的光能量，此时半像高为y′，对应的视场角称为临界探测半视场角θ′[9]，如图1(a)所示，θ′>θ，因此，可以通过改变像面离焦增大激光通信接收视场角。图1(b)为离焦时不同视场下，探测器面光斑示意图。由图1可知，在满足通信所需最低能量的前提下，采用离焦的方法增大接收视场角是可行的。

通过对理想离焦光学系统模型分析(图1(a))可知，离焦光斑半径r0与接收系统的焦距f，接收孔径D以及离焦量大小Δx有关，当探测器处于焦平面前Δx处的离焦面时，可由几何关系推导得到光学接收系统的像面离焦光斑半径模型

(2)

式中，δ为实际设计中焦平面圆斑半径，光学系统设计越理想，δ越小，若为理想光学系统，则光线在焦面处汇聚成一个理想点，即

(3)

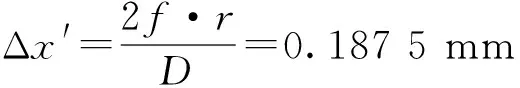
2.2 通信接收离焦光斑能量模型

要增大视场角，首先要保证探测器接收到的能量PAPD要大于激光通信最小能量Pmin，即

PAPD>Pmin,

(4)

假设光斑能量均匀分布，则探测器接收到的离焦光斑能量模型为

(5)

式中，S为光斑与探测器的重叠面积，r0为光斑半径，Pr为离焦接收能量。当发射端发射的能量不变时，离焦接收能量Pr仅受链路及系统本身损耗影响，可以表示为

Pr=Pt-γt-γa-γr-γG-γf,

(6)

式中，Pt为发射端发射能量；γt为发射端系统损耗；γa为大气损耗，假设大气能见度为8 km，则每千米大气衰减1.6 dBm[21]；γr为接收端系统损耗；γG为几何损耗；γf为光纤耦合损耗。其中几何损耗可以表示为:

(7)

式中，Dr为接收孔径大小，L为通信距离，ω为激光发射光束束散角。表1、表2分别表示初始链路计算参量的输入值以及不同通信距离对应的离焦接收能量的大小。

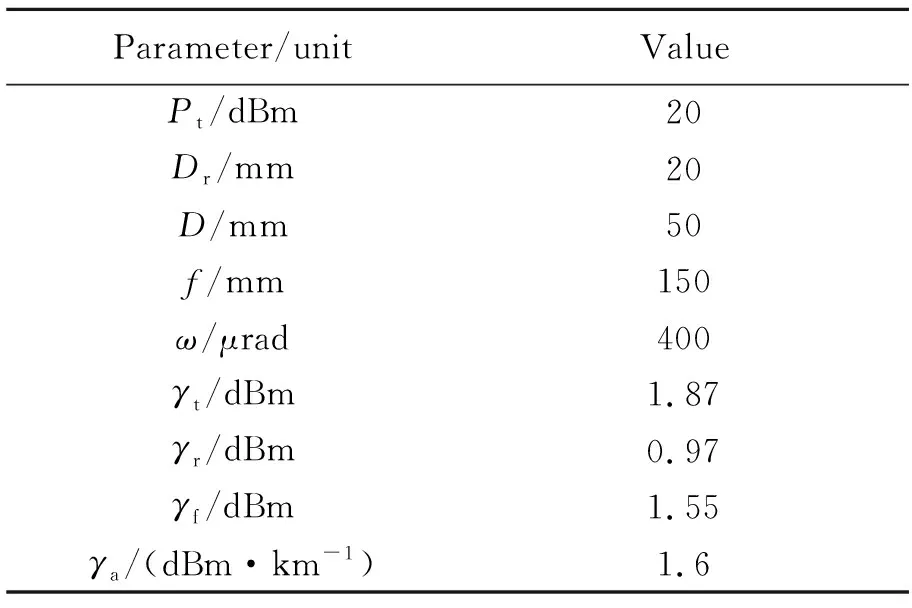
表1 链路计算输入参数Tab.1 Input parameters of link calculation

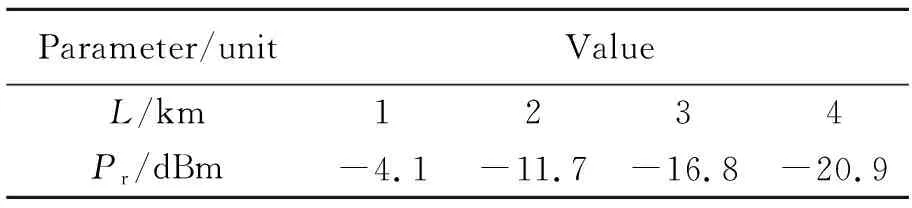
表2 不同通信距离下的离焦接收能量Tab.2 Defocus receiving energy at different communication distances

3 离焦光斑面积及接收能量情况

图2 不同离焦量和视场下的光斑示意图 Fig.2 Schematic diagram of spot at different defocusing amount and FOV

由公式(5)可知，光斑在探测器面上所占的面积S对探测器接收到的能量PAPD有很大影响。图2(a)、图2(b)和图2(c)依次表示随着离焦量的扩大，同一视场下光斑与探测器位置关系，图2(c)和图2(d)表示相同离焦量时，不同视场下的光斑与探测器位置关系。本文根据光斑占探测器面积的大小，分两种情况讨论：光斑部分覆盖探测器面和光斑完全覆盖探测器面。

3.1 光斑部分覆盖探测器面

当光斑部分覆盖探测器面时，光斑与探测器重叠面积S如图3所示。

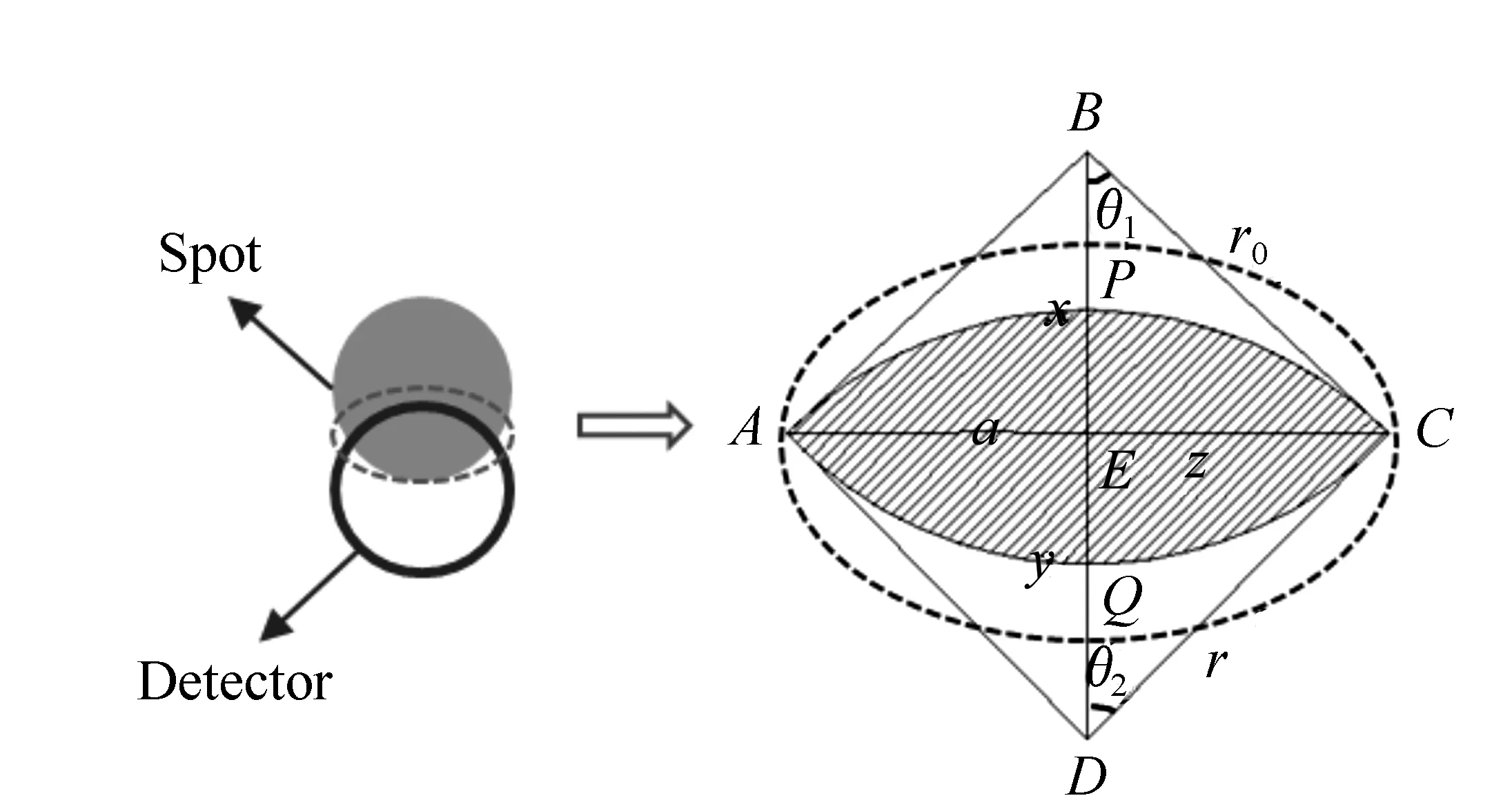
图3 光斑与探测器重叠面积示意图 Fig.3 Schematic diagram of overlapping area of spot and detector

图3中AB=BC=r0(光斑半径)，AD=DC=r(探测器半径)，设光斑中心到探测器面中心的长度为BD=a， ∠CBD=θ1，∠CDB=θ2，AE=EC=z，BE=x，ED=y。由几何关系可知:

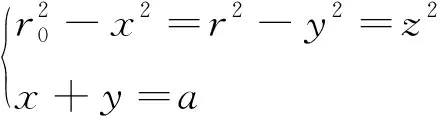
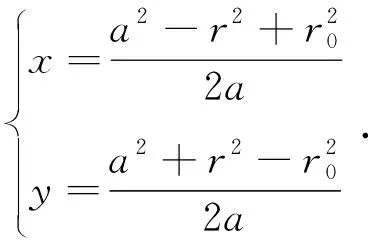
(8)

因此，可求得重叠面积S大小

(9)

其中

(10)

(11)

根据公式(11)可知，影响重叠面积S的主要因素为离焦量Δx和半视场角θ。图4模拟了视场角为1 mrad时，离焦量Δx与光斑占探测器面积S的关系。由图4可知，重叠面积S随着离焦量的扩大而增加，在光斑即将完全覆盖探测器面时，S增长幅度变缓，完全覆盖后不再变化，趋于一条直线。

图4 重叠面积与离焦量的关系曲线 Fig.4 Relation curve of overlapping area and defocusing amount

当半视场角从0增加到极限角θmax时，探测器接收能量恰好下降为临界接收能量Pmin，根据公式(4)和(5)可推出

(12)

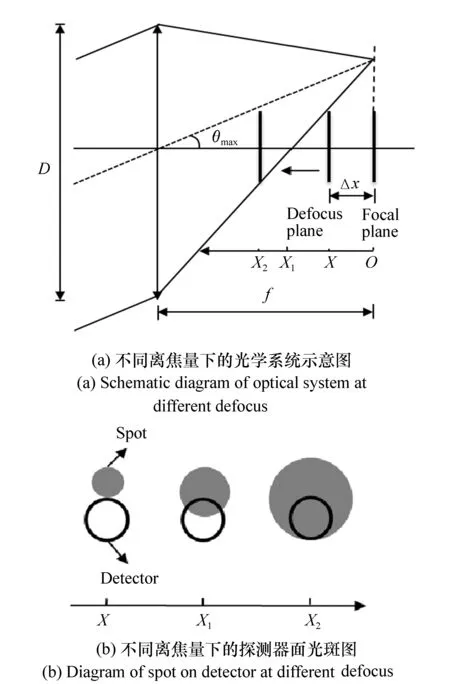
图5 固定视场下的离焦量变化示意图 Fig.5 Schematic diagram of defocusing amount change at fixed FOV

即

(13)

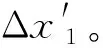
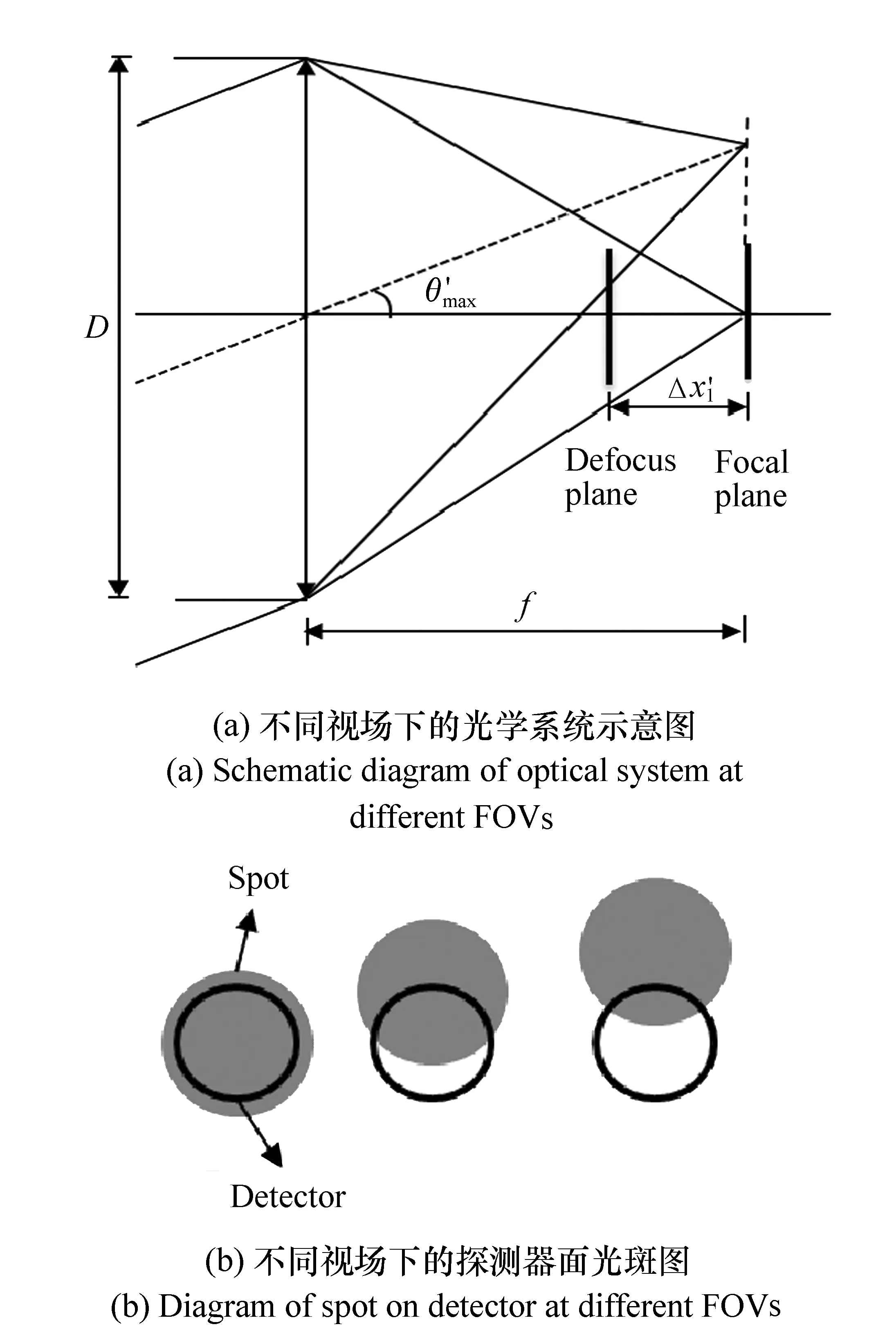
图6 固定离焦量下的视场变化示意图 Fig.6 Schematic diagram of FOV change at fixed defocusing amount

(14)

3.2 光斑完全覆盖探测器面

当光斑完全覆盖探测器面时，重叠面积S即为探测器的面积S=SD=π·r2，由公式(3)可知，当接收口径D和系统焦距f不变时，光斑半径r0随着离焦量的扩大而增大。当离焦接收能量Pr不变时，由公式(5)可知，PAPD随着离焦量的扩大而逐渐减小。图7(a)即为当视场角为1 mrad，离焦接收能量为-4.1 dBm，光斑完全覆盖探测器面时，探测器接收能量与离焦量的关系，图7(b)展示了光斑完全覆盖探测器面时，光斑与探测器的几何位置关系。

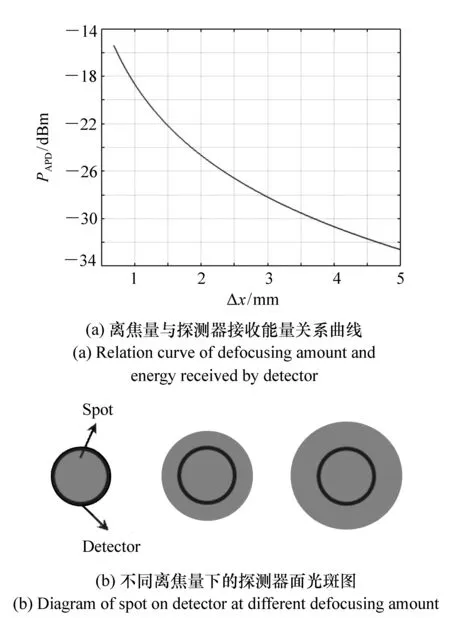
图7 光斑完全覆盖探测器面下的探测器接收能量与离焦量的关系图 Fig.7 Relation diagram of energy received by detector and defocusing amount under the condition of detector completely covered by the spot

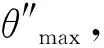
(15)

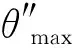
图8 固定重叠面积下的最大视场示意图 Fig.8 Schematic diagram of maximum FOV at fixed overlapping area

4 视场角的影响因素分析

以探测器灵敏度为通信所需最小接收能量的参考标准，影响通信视场角的两个主要因素是离焦接收能量和离焦量。本节以满足最小通信接收能量(-35 dBm)为前提，分析并对比了离焦接收能量和离焦量对接收视场角的影响。

传统非离焦光学系统的视场只与像面(探测器面)及焦距有关，假设焦距f=150 mm，探测器半径r=31.25 μm，则根据公式(1)可算出未离焦光学系统的接收视场角2θ≈0.417 mrad，当离焦接收能量为-4.1 dBm时，离焦与非离焦情况下接收视场对比如表3所示。

根据第3.1节光斑部分覆盖探测面时，探测器接收能量公式(12)分析可知，当离焦接收能量Pr已知，不同视场情况下，可以求出不同离焦量Δx下的探测器接收能量PAPD。结合公式(3)、(5)、(9)和(10)分析推导，图9模拟了离焦接收能量为-4.1 dBm，视场角分别为1、1.5、2和2.5 mrad四种情况时，不同离焦量与探测器接收能量的关系。

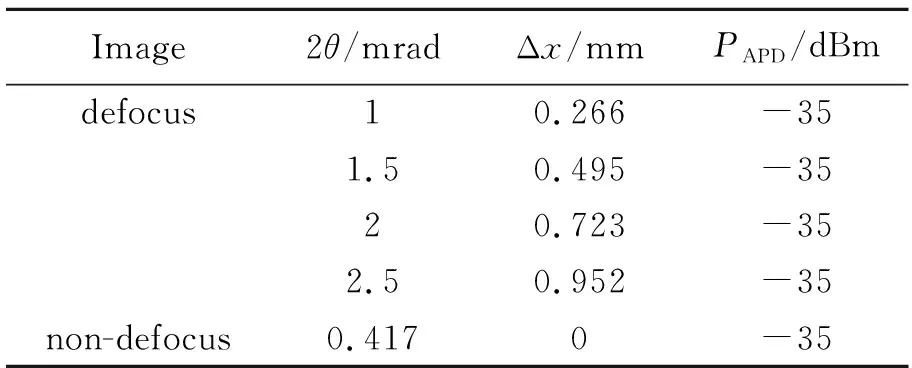
表3 离焦与非离焦接收视场对比Tab.3 Contrast of FOV under the conditions of defocus and non-defocus

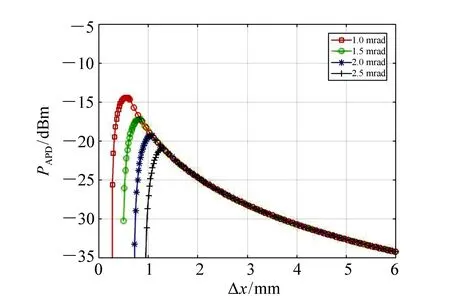
图9 不同视场下的探测器接收能量与离焦量的关系曲线 Fig.9 Relation curves of energy received by detector and defocusing amount at different FOVs

由图9可知，在同一视场下，存在一个最佳离焦量，可以实现探测器接收能量最大；不同视场角下，对应刚好满足通信所需最低能量(-35 dBm)的离焦量不同，且视场随着离焦量的扩大而增大。当光斑完全覆盖探测器面时，重叠面积S固定，等于探测器面积。根据公式(3)和公式(5)可知，此时探测器接收能量只与离焦量Δx以及离焦接收能量Pr有关，且当离焦量Δx固定时，探测器接收能量PAPD与离焦接收能量Pr成正比，提高离焦接收能量能增大探测器接收的能量，当PAPD>Pmin时，由图9可知，增大视场角会降低探测器接收能量，直至降至刚好满足通信所需(-35 dBm)。综上分析可知，离焦接收能量和离焦量都能影响通信接收视场角的大小。

图10 不同离焦接收能量下探测器接收能量与视场角的关系曲线 Fig.10 Relation curves of energy received by detector and FOV at different defocus receiving energy

4.1 离焦接收能量

离焦接收能量Pr除了受发射功率以及光学镜头透过率影响外，主要受传输距离的影响。根据表1和表2仿真的不同传输距离时的离焦接收能量，图10模拟了离焦量为0.5 mm(>Δx′)，离焦接收能量分别为-4.1、-11.7、-16.8和-20.9 dBm四种情况时，不同视场角与探测器接收能量的关系。

图11 光斑与探测器位置关系图 Fig.11 Position relationship between spot and detector

由图10可知，当视场角从0增大到0.7 mrad时，探测器接收能量不变，这是因为视场角从0到0.7 mrad这段区间光斑一直占满整个探测器面，如图11(a)所示；当视场角大于0.7 mrad时，光斑不全覆盖探测器面，探测器接收能量逐渐减弱直至不再满足通信所需或者探测器面完全没有光斑，如图11(b)所示。当离焦接收能量从-20.9 dBm逐渐提高到-4.1 dBm时，随着探测器接收能量的降低，视场能增大的量逐渐减小。这是由于探测器接收能量越小，视场角越大，此时光斑占探测器面的面积S越小，且趋于零，所以即使增加接收能量，视场角可增加范围比较小。假设能满足通信所需的最小能量为-35 dBm，且离焦接收能量为-4.1、-11.7、-16.8和-20.9 dBm时，对应的视场角分别为1.24、1.38、1.46和1.51 mrad，因此提高离焦接收能量(即增加发射功率或者缩短通信距离)能增加接收系统的视场角，但是增加幅度不明显，Pr从-20.9 dBm提高到-4.1 dBm，视场仅增大了0.27 mrad。从实际通信实验考虑，0.27 mrad的视场角扩增，对离焦接收能量功耗较大，但是在降低对准难度方面的效果并不十分明显。

4.2 离焦量

离焦量主要影响光斑半径，随着离焦量的扩大，光斑面积逐渐增大，当离焦量扩大到临界离焦量Δx′时，光斑恰好完全覆盖探测器面。图12模拟了接收总能量为-4.1 dBm，离焦量分别为0.2、0.4、0.6、0.8和1 mm五种情况下，视场角与探测器接收能量的关系。

图12 不同离焦量下探测器接收能量与视场角的关系曲线图 Fig.12 Relation curves of energy received by detector and FOV at different defocusing amount

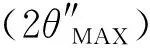
为0.85、1.29、1.73、2.2和2.6 mrad。离焦量从0.2 mm扩大至1.0 mm，视场角增大了1.75 mrad。在实际的设备装调中，将像面调整至焦平面前1 mm处的位置，操作简单且没有其余附加损耗，而1.75 mrad的视场角增量对对准难度降低的效果比较明显。

5 结 论

本文以探测器接收能量能够满足通信最低要求为前提，建立了光学接收系统模型图和通信接收能量模型；从光斑与探测器重叠面积出发，推导了探测器接收能量与接收视场角、离焦接收能量和离焦量的相互关系；以探测器接收能量满足通信所需(-35 dBm)为前提，对比分析了离焦接收能量和离焦量对增大接收视场角的作用，得出提高离焦接收能量以及扩大离焦量都能增加接收视场角，扩大离焦量的效果相对比较明显。当离焦接收能量为-4.1 dBm，离焦量从0.2 mm扩大到1.0 mm时，接收视场能达到的最大值能增加1.75 mrad；当离焦量为0.5 mm，离焦接收能量Pr从-20.9 dBm提高到-4.1 dBm时，接收视场仅能增加0.27 mrad。仿真结果验证了离焦对增大系统视场角的作用，并对后续的实验及系统设计提供了参考和帮助。