太阳辐射计的衍射效应修正
刘国栋,方 伟,宋宝奇,叶 新,王 凯
(1.中国科学院 长春光学精密机械与物理研究所,吉林 长春 130039;2.中国科学院大学,北京 100049)
1 引 言
太阳辐射是地球最主要的能量来源,除了核能,火山爆发等,地球上大部分的能量都直接或间接地来自太阳辐射,太阳辐射对地球的生态和环境具有深刻的影响[1]。为了自身的长久可持续发展,人类很早就开始了对太阳辐射的监测与研究。太阳辐射的测量主要是指太阳总辐照度(Total Solar Irradiance,TSI)测量和太阳光谱辐照度(Solar Spectral Irradiance,SSI)测量。这些太阳辐射的监测数据,可以应用到很多科学领域,如气候模型的推演、太阳物理研究、地球辐射收支平衡的研究等等,随着研究的深入,这些领域对太阳辐射数据的测量精度要求越来越高。
太阳绝对辐射计是一种对太阳总辐照度进行监测的仪器[2],其测量精度直接影响太阳辐射数据的可信度。衍射效应是太阳绝对辐射计系统误差的主要来源之一,要获得精确的测量数据,必须对其进行修正。但是在辐射计量领域,衍射效应的修正一直是一个难以解决的问题。一方面是因为衍射效应广泛存在于光学系统中,几乎所有对光起限制作用的器件,都会引起衍射效应;另一方面,衍射效应难以用实验测量,即使能测量,实验中的不确定度也超过能容忍的范围。因此,对衍射效应的研究主要侧重于数学计算上。
辐射计量中衍射效应数学计算在国外有较多的研究。1962年,C.L.Sanders和O.C.Jones在用铂点黑体实现光单位时,用夫琅和费衍射理论证明了接收像面中心照度比通过几何光学计算结果低大约0.25%,证明了衍射效应对精密辐射测量的显著性影响。W.R.Blevin在实测Stefan-Boltzman常数的工作中发现这项误差甚至可达到0.5%。此后,衍射效应成为黑体辐射测量中不可忽视的因素[3]。近几十年来,随着人类活动走向太空,发射了各种太阳辐射监测仪器,由于对其精度的要求逐渐提高,衍射效应的数学计算,逐渐开展起来。目前在国外,衍射效应的修正已经开始应用于辐射计的测量结果,获得较高的辐射测量精度,然而国内却尚未开展该方面的工作,严重制约了我国在辐射计量领域的发展。本文根据对衍射效应问题的研究,提出一种实用化的计算方法,精度高,计算简便,实现了对太阳辐照绝对辐射计(Solar Irradiance Absolute Radiometer,SIAR)的衍射效应修正。
2 衍射效应计算方法
2.1 衍射效应公式的推导
为了便于论述,本文做如下定义:衍射效应是指由于光的衍射,探测器接收的辐射通量与几何光学期望值的比,是一个与光的衍射有关的“物理量”,用F表示。
根据Kirchhoff衍射理论和傍轴光学近似,点光源通过光阑衍射后的电场强度为:
(1)
其中,C=(d-1+d′-1)/2是与结构有关的系数,相关参数如图1所示,它表示了x′与x电场强度的相互关系。考虑到能量密度W=C|U(x,t)|2,并做一定的坐标变换,可以得到:
(2)
其中,R表示光阑的半径,r表示x′到光轴的距离,ρ=r″/R,u=。2qCR2,v=|2qCRr|。
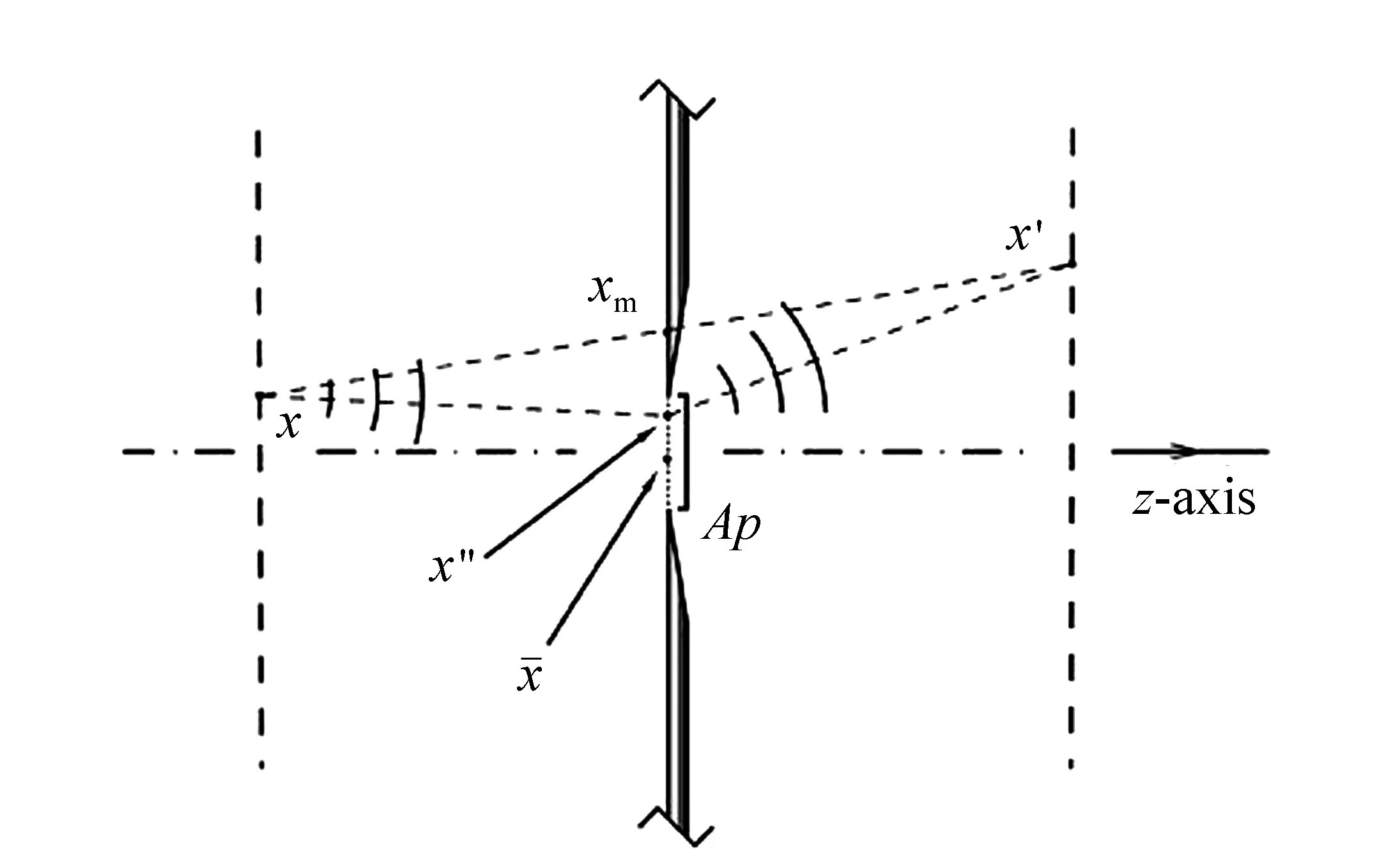
图1 点光源衍射讨论中的参量 Fig.1 Parameters in the discussion of point source diffraction
式(2)表示了x′与x之间能量密度的关系。而在几何光学中,x′与x之间能量密度的关系如下:
(3)
式中,Θ(x)是Heaviside阶跃函数。
因此,|S(r′)/SG(0)|2就表示点x′处的衍射效应,其表达式由Lommel函数[4]给出:
(4)
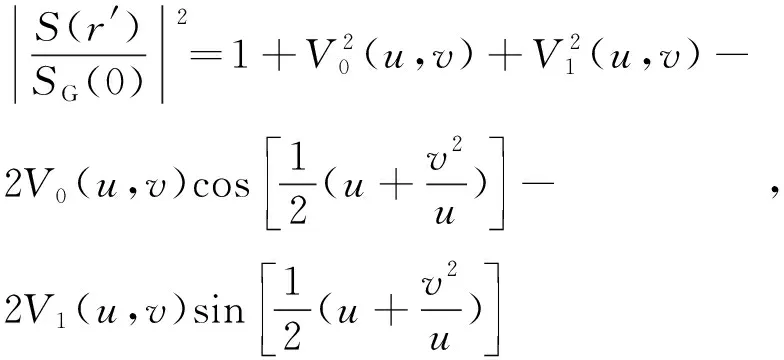
(5)
式中,Un(u,v)和Vn(u,v)可以用n阶贝塞尔函数来表示
(6)
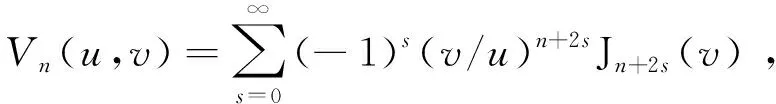
(7)
式(4)和式(5)是等价的,当r′>R时,式(4)更简便,而当r′>R时,式(5)更简便。
实际的辐射测量,是对整个探测平面的能量密度进行积分,为此,引入一个新的量L(u,v0),表示整个探测平面的衍射效应[5],它相当于|S(r′)/SG(0)|2在整个探测平面的积分,类似于|S(r′)/SG(0)|2的推导,Wolf给出了L(u,v0)的表达式:
当v0>|u|时,
(8)
当v0<|u|时,
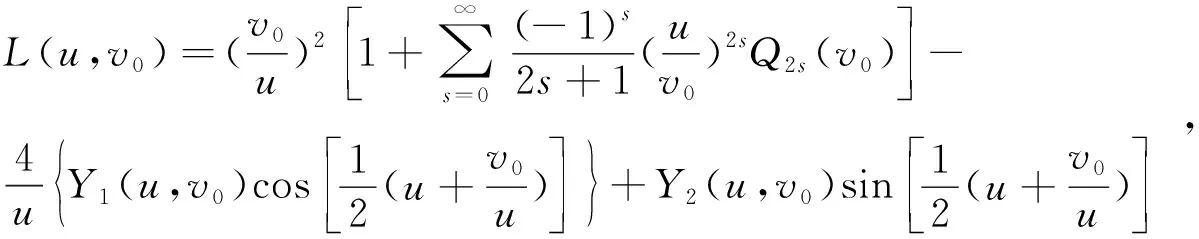
(9)
式中,Q2s(v0)和Yn(u,v0)表示如下:
Jp+1(v0)J2s+1-p(v0)]
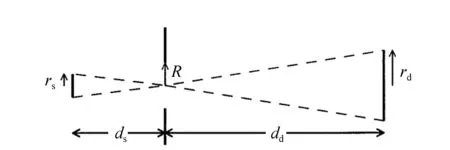
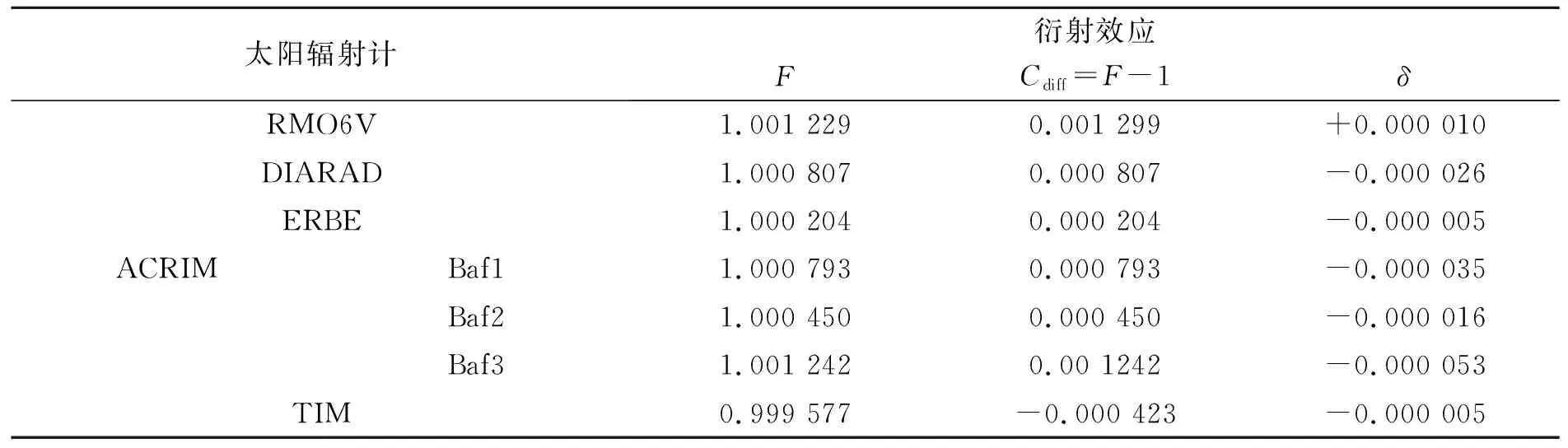
设探测器平面上所有点的集合为{x′},探测器边缘上的点满足v=v0,探测器内部的点满足v 实物光源常常可以看作无数个相互独立的点光源的集合,在式(8)和式(9)的基础上,E.L.Shirley推导出了适用于扩展光源的公式[6]: (10) 若仅仅在几何光学范畴考虑,则可以很容易求得探测器接收的总能量ΦG(λ),其表达式跟具体的光学结构有关。因此,总的衍射效应就可以表示为: (11) 现在通过图2对式(10)的参数进行说明,可以看出,该光构中包含了扩展型朗伯光源(Source),光阑(Aperture)和探测器(Detector)三个要素,R、rs、rd、ds、dd表示3个要素构成的几何参数。事实上,对该结构的研究是辐射计量中研究最多的问题之一,称为SAD问题。 图2 SAD结构 Fig.2 Structure of SAD F1:u F2:y>vm(1+σ) F3:vm(1-σ) (12) 对于F1情况,光阑会限制光的几何传输路径,而在F2中则不会。F3情况会导致探测器边缘位于光束与阴影区域的交界附近,衍射效应分析复杂,是结构设计中需要避免的情况。式(8)和式(9)是L(u,v)分别在F1和F2情况下的表达式,只不过取v=vm(1+σx)。在几何光学范畴内考虑,ΦG(λ)在F1和F2情况下可以表示为 (13) 综合式(10)、式(11)和式(13)可得总的衍射效应为: (14) 该式表示了SAD结构对波长为λ的光的衍射效应,然而太阳辐射计中所测光源是太阳,是一个宽光谱的普朗克光源。实际操作中,可以将太阳辐射的等效波长λeff≈902.792 042 6 nm应用于式(14)[8]。 由于L(u,v)包含复杂的n阶贝塞尔函数,对式(14)直接积分是困难的。实际操作中,常常根据贝塞尔函数的渐近性质对L(u,v)进行简化。 当v>|u|时,Focke在前人的工作基础上给出了L(u,v)的渐近形式[9], (15) (16) (17) (18) 其中σk是由简单函数Wk(x)决定的变量 (19) W0(x)=1,W3(x)=x3+4x2+x, W1(x)=x,W4(x)=x4+11x3+11x2+x, W2(x)=x2+x,W5(x)=x5+26x4+66x32611x2+x. (20) 通过上述渐近处理,可以将L(u,v)表示为简单函数,则式(14)就转化为简单函数的线性积分,大大简化了计算量。 为了验证上述简化方法的准确性,本文参考国外一些已经进行过衍射修正的辐射计结构,将使用本文方法计算的结果与其报告的结果进行对比。表1是国外几个辐射计的SAD结构参数以及衍射效应的计算结果[11]。计算过程是对公式(14)的数值计算,该过程采用精确的L(u,v)(含有n阶贝塞尔函数),计算结果较为精确。可以看出太阳总辐照度测量中衍射效应在10-3~10-4之间,已经成为精确测量中不可忽视的重要因素。 表1 几种太阳辐射计的衍射效应Tab.1 Diffraction effects in some radiometers 表2是采用本文简化方法计算得到的衍射效应,也就是考虑L(u,v)的渐近性质,进行较为简便的线性积分。可以看出,计算结果与表1的偏差在10-5~10-6之间,远小于衍射效应值,从而证明本文的方法在简化运算的同时兼顾了计算结果的准确性。 表2 采用简化方法的衍射效应值Tab.2 Diffraction effects by using simplified method SIAR是一种利用电替代原理对太阳辐射进行测量的仪器,其构造如图3所示,主要结构包括锥腔,光阑结构,热沉以及相关的电路模块[12]。 图3 SIAR剖面示意图 Fig.3 Profile of SIAR SIAR的光阑有6个:主光阑,视场光阑,4个消杂光光阑。视场光阑在前,主光阑在后并靠近锥腔,半径为4 mm。整体结构视场半角为1°,相邻光阑距离为20 mm光阑分布如图4所示。 图4 光阑的几何分布 Fig.4 Positions of the apertures 应用上述SAD结构,对SIAR的衍射效应进行分析。首先由于主光阑靠近锥腔,认为通过主光阑的光都能到达锥腔,则主光阑开口相当于SAD的探测器,且rd=4 mm;太阳作为SAD结构中的扩展型朗伯光源,rs≈6.75×1011mm,距离光阑距离ds≈1.5×1014mm, 由于太阳到地球表面的视场半角约为32′,位置在前的光阑不会遮挡后面光阑的几何光学路线[13],因此视场光阑和4个消杂光光阑可以作为SAD结构中的非限制光阑,引起F2类型的衍射效应。SIAR的衍射效应问题可以分解为5个SAD问题。视场光阑与随后的4个消杂光光阑用Apx(x=1,2,3,4,5)表示,具体参数如表3所示。 根据L(u,v)在v<|u|时的渐近性质,利用式(14)进行数值积分得到每个光阑引起的衍射效应以及总的衍射效应,如表4所示。 表4 SIAR的衍射效应Tab.4 Diffraction effects in SIAR 从表4可以看出,SIAR总的衍射效应达到0.274%,而根据90年代给出的太阳总辐照度为(1 365.4±1.3) W/m2,不确定度占0.095%,由此可见,由衍射效应引起的误差是相当显著的[14],是精确测量中不可忽视的重要因素。另外由于前一级光阑不会遮挡后一级光阑的几何传输路径,衍射效应会随消杂光光阑个数的增加而逐级累加。 辐射计的衍射修正因子Cdiff定义为[15]: (21) 太阳辐射计所测辐射数据,需要定标到国际辐射基准(WRR)。具体做法为:在相同时间,相同实验环境下,SIAR与WRR同时对太阳辐射进行监测,得到的结果分别为TSI|SIAR,TSI|WRR,则SIAR的定标系数为 (21) WRR Factor越接近1,则表明辐射计的测量准确度越高。表5是未经过衍射修正的SIAR的定标系数[16]。 表5 衍射效应未修正的WRR FactorTab.5 Diffraction effects uncorrected WRR Factor 对SIAR进行衍射效应修正,则定标系数为 (22) 表6是经过衍射修正后SIAR的定标系数,可以看出经过衍射修正后,SIAR-4B和SIAR-4D的定标系数都明显地趋近于1。而对于SIAR-2C和SIAR-4A,衍射效应造成的系统误差,使得定标系数从小于1变成大于1,之所以没能更靠近1,是由其他的系统误差导致的。因此,衍射修正降低了辐射计的一部分系统误差,提高了SIAR测量数据的准确度。 表6 衍射修正过的WRR FactorTab.6 Diffraction effects corrected WRR Factor 本文从Kirchhoff衍射理论出发,根据高斯光学近似,逐步推导出了衍射效应下点与点、点与面、面与面的能量传输关系,最终给出了衍射效应计算的一般公式。为了便于计算,构建了用于衍射分析的SAD模型,重点分析了F1和F2两种衍射类型,最后根据渐近性质,提出了简便的计算方法。根据SIAR的光阑结构特点,将其衍射效应分解成5个SAD问题,使用简化的方法分别计算衍射效应,最后按照累加原则,得到总的衍射效应。由于衍射效应与辐射计的衍射修正因子互为倒数关系,从而给出了衍射修正因子,这是国内辐射计首次实现对衍射效应的修正。根据衍射修正结果,计算4个型号的SIAR相对WRR的定标系数,结果表明四个SIAR中衍射效应引起的系统误差被修正,提高了测量结果的准确度。
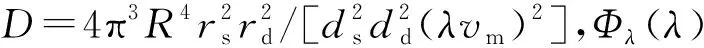
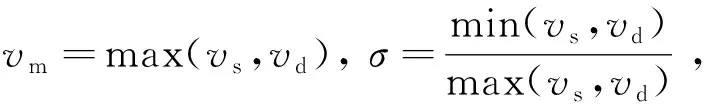

2.2 简化的计算方法
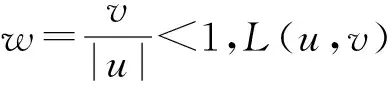
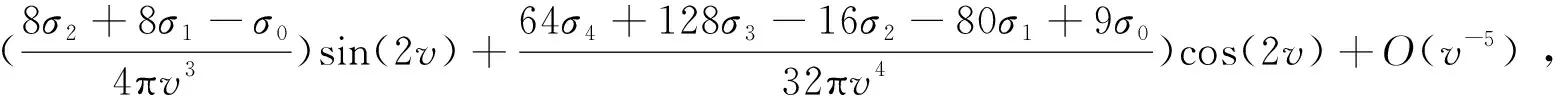

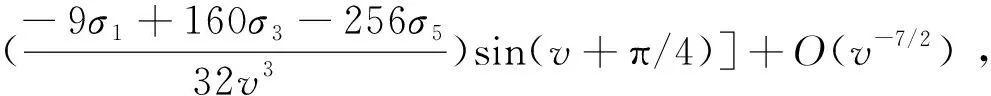
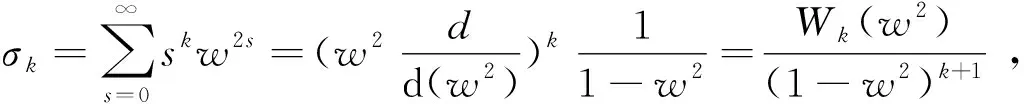

3 SIAR衍射效应的修正

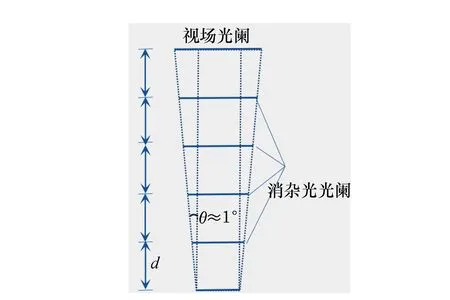


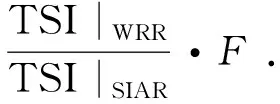

4 结 论

