浅析求二元函数极限的几种方法

熊允发, 管 涛

(中国人民公安大学信息技术与网络安全学院， 北京 100038)

0 引言

在几乎所有版本《高等数学》教材中，关于二元函数极限的内容，都是粗略带过，介绍的都极其简单，从未涉及到求极限的具体办法。为了弥补这一缺憾，让学生们更全面、深入地学习二元函数微积分，作者结合近三十多年的教学实践与体会，将求二元函数极限的方法作一总结归纳，以期对广大教师与学生有一定的帮助启迪。

1 二元函数极限的概念和性质

根据定义，至少有以下3点应引起我们重视：

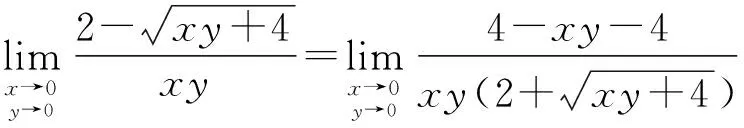
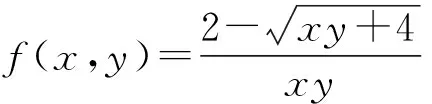
其二，二元函数极限的复杂性。由于二元函数极限定义中的动点P(x,y)趋向于点P0(x0,y0)的方式是任意的，因而平面上的点趋向于P0的方式就有无穷多种。这比起一元函数当x→x0时的极限只有左右两侧的情形，要复杂的多。但不论变量的变化多么复杂，且在多条路径上的极限始终都是唯一的[2]。

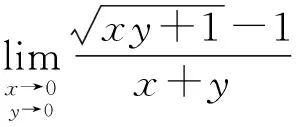
故原极限不存在(因为沿不同路径时极限不唯一).

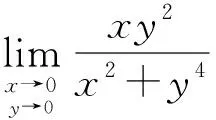
证：因为当点P(x,y)沿抛物线x=ky2趋向于点(0,0)时，

由于该极限的取值是随着k的值不同而改变，所以原极限不存在。

这里顺便说一下，因为极限的唯一性，如果在求极限值时出现有两个或以上不同值时，就意味着极限不存在。所谓极限为∞，这是一种特殊的描述方式，可以近似的理解为它是无穷小量的倒数。因此极限不存在与极限为∞不完全是一回事，两者有区别。

其三,要严格区分二重极限与累次极限的关系。尽管两者都是极限，其性质不一样，含义也不相同[3]。结合下面的例子加以说明。

例4 设

试讨论下面3种情形的极限。

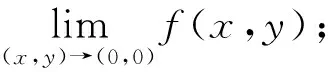
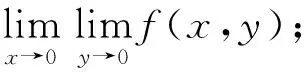
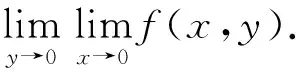
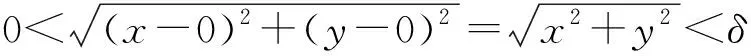
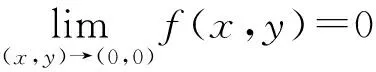
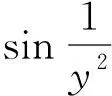
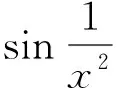
由此可以看出，上例①中二重极限为0，而②③两个累次极限均不存在。因此，重极限与累次极限不是一个概念，二者有本质区别[4]。

2 求二元函数极限的几种方法

(1) 利用连续函数的定义及初等函数的连续性求极限

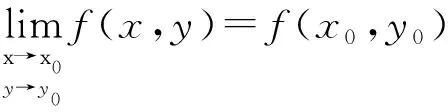
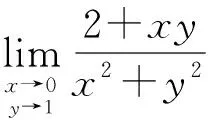
解：∵(x2+y2)|(0,1)=1≠0，

② 如果(x0,y0)不是f(x,y)的连续点，则可先通过分子、分母有理化等方法使之变连续后再代值。

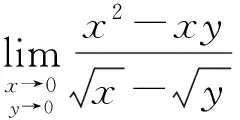
解：当x→0，y→0时，分子分母同时趋向于0，则可先将分母有理化。

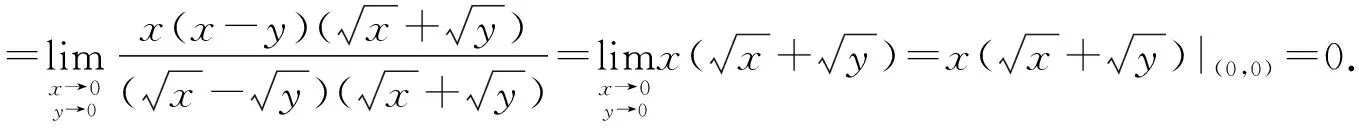
(2) 利用夹逼准则来求极限

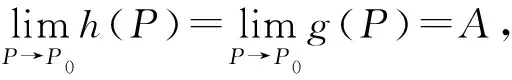
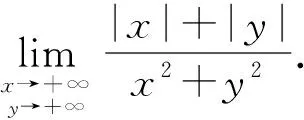
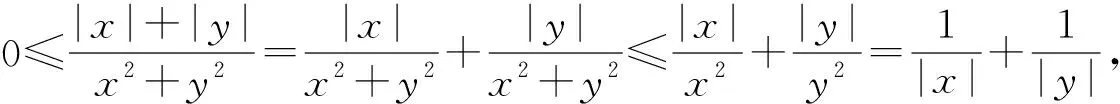
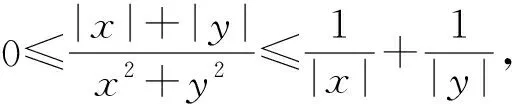
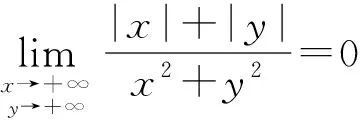
(3) 利用一元函数中的两个重要极限公式来求极限

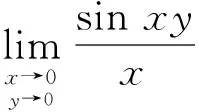
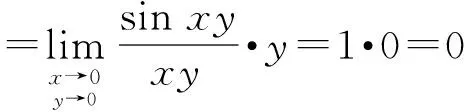
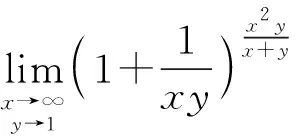
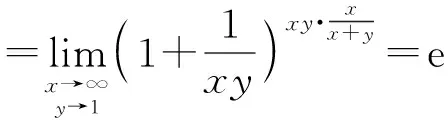
(4) 利用一元函数极限的性质求极限

有界变量与无穷小量的乘积仍为无穷小量[5]

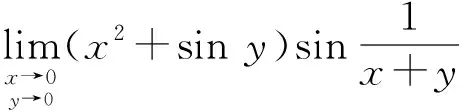
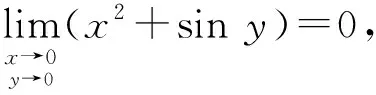
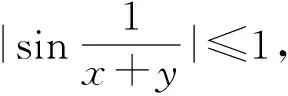
(5) 利用等价无穷小代换求极限

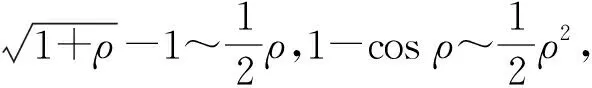
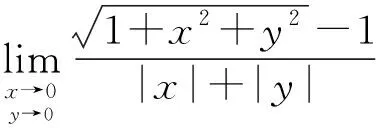
解：当x→0，y→0时，x2+y2→0，

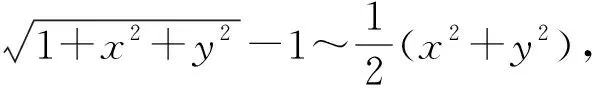
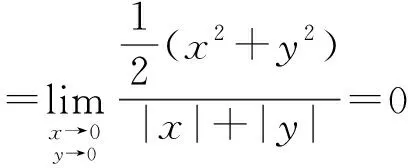
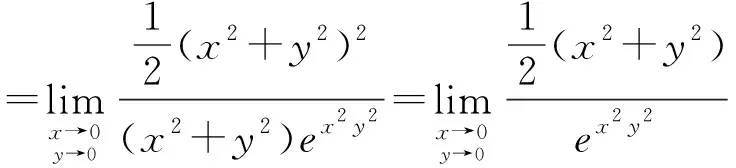
=0

(6) 利用变量代换，将二元函数转换为一元函数再求极限

如令t=x2+y2

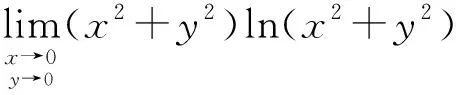
解：令t=x2+y2，

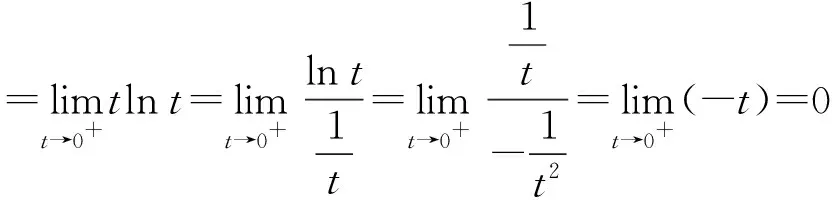
3 结语

由二元函数极限的定义，可以看出，要学好这部分的内容，真正做到会求二元函数的极限不是一件容易事，必须要脚踏实地，认真领会其精神实质，在实际动手操作中真正领悟二重极限的知识内涵。