基于等效元素法的机电作动器传动机构动力学建模与分析

刘 海，段小帅，黄 建

(北京自动化控制设备研究所，北京 100074)

0 引言

目前，机电作动器因其体积小、输出功率大、控制精度高等优点，广泛应用于运载火箭、导弹、卫星、智能弹药等控制领域，成为火箭推力矢量控制、飞行器翼面等的主要执行机构[1-2]。随着军事现代化的发展，飞行器的飞行速度日益加快，超高音速的飞行器对其伺服机构也提出了高动态响应、高刚度、高承载等严格要求[3-4]。此时，机电作动器设计只考虑机构运动学已不够全面，动力学分析已成为不可忽视的一项内容。机电作动器动力学分析属于多刚体动力学分析范畴，常规的算法大多采用牛顿-欧拉方法、拉格朗日法、罗伯森-维滕伯格方法、凯恩方法以及休斯敦法[5]。由于机电作动器传动机构刚体数目多、传动链长、连接约束多，用常规算法建立方程不仅工作量大，而且不便于计算机求解。

本文引入集中质量等效元素法，建立机电作动器的动力学解析模型，并根据工作需求，在ADAMS平台进行虚拟样机动力学逆求解仿真[6]，开展机电作动器系统动力学研究。

1 动力学模型

1.1 机电作动器传动机构

机电作动器的传动机构以谐波减速器、行星减速器和滚珠丝杠为主，滚珠丝杠以其传动刚度高、结构尺寸紧凑、运动平稳等优点广泛应用于电动伺服领域[7]。图1所示为某机电作动器的传动原理图，传动机构由齿轮减速器、滚珠丝杠以及连杆机构组成。

1.2 机电作动器动力学模型

集中质量等效元素法在一般系统动力学方法的基础上，引入单元等效和等效系统集成的概念，实现了有限构件组成的复杂机械系统动力学建模[8-10]。

如图1所示，将模型划分为6个单元，其中3、4、5、6单元可直接向质心等效。1、2单元属于杆件单元，如图2所示，根据惯性等效原则，等效单元的惯性矩阵和原构件单元的惯性矩阵完全相同，将分布质量的构件凝聚到构件的两端，得到其等效单元如式(1)、式(3)所示。

(1)

(2)

(3)

单元节点号和系统节点号之间的关联矩阵Nm表达如下

(4)

根据关联矩阵，以有限元方法对系统质量阵进行组装得到等效系统质量Ms

(5)

系统等效力阵为

(6)

设置系统位移坐标ui(i=1,2,3,…,8)，机电作动器系统为单自由度系统，设置系统广义坐标为φ1

(7)

式中：zi为齿轮齿数(i=4，5，6)；φ2为连杆与地面惯性坐标系x轴夹角；L0为滚珠丝杠导程。

将系统位移坐标ui对系统广义坐标φ1求一次偏导得到一阶雅克比矩阵，将系统位移坐标ui对系统广义坐标φ1求二次偏导得到二阶雅克比矩阵。

(8)

(9)

式中：c1=cosφ1，c2=cosφ2，s1=sinφ1，s2=sinφ2。

将系统等效质量阵Ms、系统等效力矩阵Fs、一阶雅克比矩阵Tia、二阶雅克比矩阵Tiab代入一般系统动力学方程得机电作动器系统动力学方程。

(10)

系统动力学方程求解有正、逆两种方式，逆解方式是已知系统的运动轨迹、加速度、位移等运动学参量，求系统的载荷变化情况。本文在ADAMS中采用逆方式求解方式，输入系统驱动位移，分析系统载荷动力学响应。

2 ADAMS平台动力学仿真

基于UG和ADAMS协同仿真，建立机电作动器仿真实体模型如图3所示。模型中将机电作动器壳体简化为大地，忽略杆件连接中的销轴，以转动副替代。在ADAMS中按照表1所示对各个部件添加材料属性，然后分别对部件添加约束条件，主要包括电机齿轮与惰轮间齿轮副、惰轮与丝杠齿轮间齿轮副、丝杠丝杆与丝杠螺母间螺旋副、丝杠螺母与连杆间圆柱副、连杆与输出轴间转动副、输出轴与大地间转动副以及相应的固定副。根据工作要求在输出轴施加静态力矩负载和惯性负载。

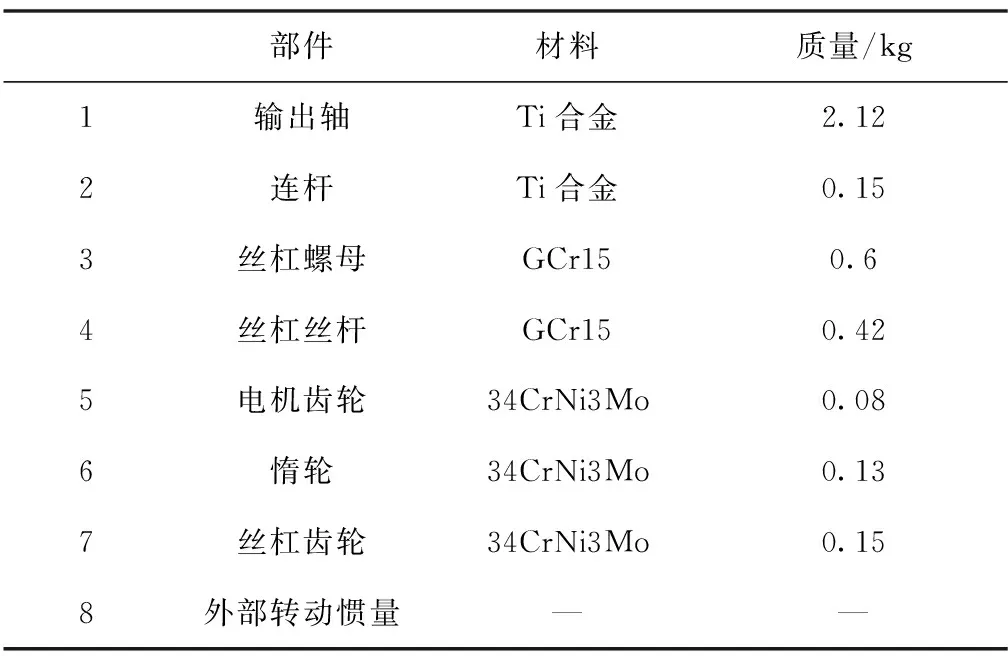
表1 部件材料属性表

2.1 30°大行程位移信号仿真分析

30°位移信号是机电作动器输出轴最大行程位移信号，为连续的+30°,0,-30°,0。当30°位移信号仿真时，改变机电作动器惯性负载工况，系统外部转动惯量分别为0kg·m2、1kg·m2、2kg·m2、4kg·m2。分析外部转动惯量对机电作动器伺服电机及减速部件滚珠丝杠的受载影响。在对30°极限位移信号进行仿真分析后，得到电机驱动力矩曲线如图4所示。在0.15s和0.45s时，输出轴分别转到+30°和-30°最大行程，电机驱动力矩在这2个时刻达到极值。

提取图中系统外部转动惯量对应电机最大驱动力矩如表2所示。随着系统外部转动惯量由0增大至4kg·m2，电机最大驱动力矩逐渐增大，动载系数Kv由1增大到1.34。此时系统结构设计只考虑静载已不满足要求，电机负载应考虑由系统外部转动惯量和自身传动机构转动惯量动载效应产生的附加载荷。

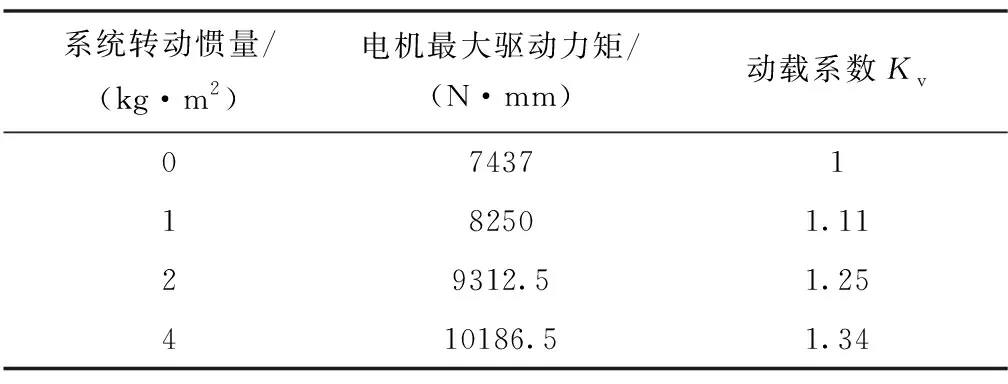
表2 电机最大驱动力矩

丝杠轴向推力曲线如图5所示。

在0.6s的仿真周期内，丝杠轴向推力随着输出轴角度呈非线性变化，在0.15s和0.45s时达到极值。丝杠轴向力同样随着系统外部转动惯量增大而明显增大，当系统转动惯量为4kg·m2时，丝杠轴向力为31676N，动载系数为1.55，如表3所示。丝杠负载应考虑由系统转动惯量及动载效应产生的附加载荷。

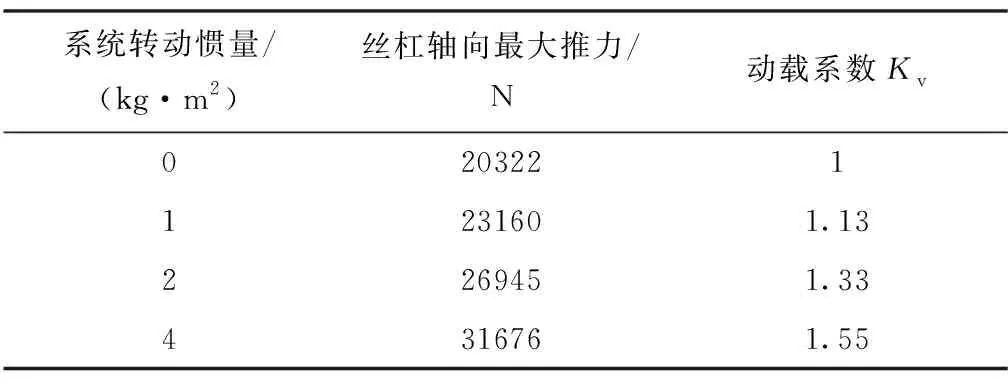
表3 丝杠最大轴向推力

2.2 8Hz频率特性仿真分析

在进行8Hz频率特性仿真分析时，电机齿轮驱动函数为幅值为A，频率为8Hz的正弦函数。通过改变驱动正弦函数幅值A，改变机电作动器系统加速度，得到不同系统加速度对应电机驱动力矩曲线如图6所示。

提取不同驱动函数幅值A工况对应电机最大驱动力矩如表4所示。当将系统转动惯量为0时，可认为无动载效应，动载系数为1；电机最大驱动力矩随着驱动正弦函数幅值的增大而增大，动载系数Kv由1增大到1.23。分析表明，随着系统工作高速化，此时系统结构设计只考虑静载已不满足要求，电机负载应考虑由系统加速度动载效应产生的附加载荷。

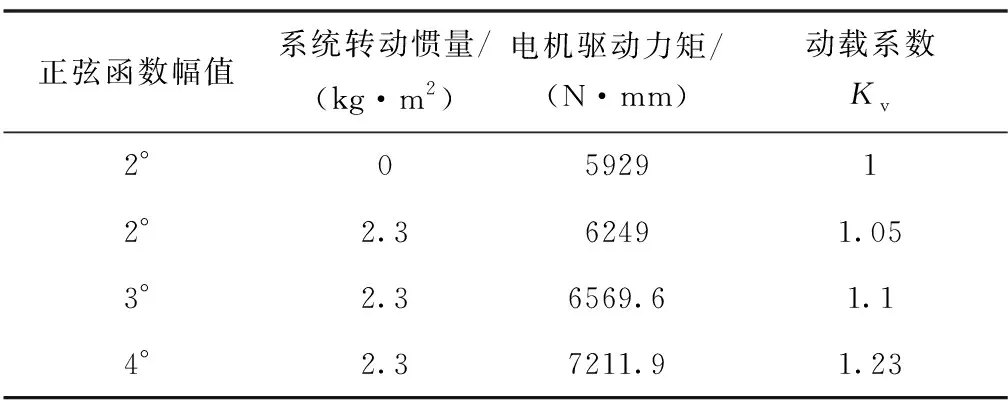
表4 电机最大驱动力矩

3 结论

1)通过引入规范化的动力学建模方法—集中质量等效元素法，分别建立机电作动器系统等效质量、系统等效力系，然后根据系统位移坐标与广义坐标之间的雅克比关系，得到一阶和二阶雅克比矩阵，据此建立了机电作动器系统动力学方程。此种建模方法步骤规范，可操作性强，且易于计算机求解。

2)结合机电作动器系统动力学方程，在ADAMS平台进行动力学逆求解，得到30°大行程位移信号和8Hz频率信号两种工况下系统载荷响应曲线。随着负载转动惯量增加，电机动载系数达到1.34，丝杠动载系数达到1.55；外部负载不变时，随着驱动信号幅值增加，电机动载最大系数为1.23，表明随着机电作动器系统外部惯性负载及系统运动速度的提高，由外部惯性负载及自身传动机构产生的动载效应明显，为机电作动器传动机构优化设计提供了理论依据。