考虑螺纹细节的螺栓预紧过程仿真分析研究
徐卫秀,王淑范,杨 帆,黄 蔚
(北京宇航系统工程研究所,北京100076)
0 引言
螺接是工业结构中的主要连接形式之一,而螺栓预紧力是影响连接结构运行安全和可靠性的关键因素,重要螺接结构需要对螺栓预紧力进行精确设计控制,保证预紧力和结构强度都能满足设计要求。现阶段螺栓预紧力设计的一些关键环节只能根据经验方法近似计算,重要环节需要依靠试验测量:
其一是扭矩系数(k)。工程上,预紧力一般通过施加预紧力矩来控制,准确确定预紧力矩和预紧力的关系,即扭矩系数,是准确控制预紧力的前提。而影响k值的因素很多,它与结构材料、表面粗糙度、镀层和润滑状态等有关。为保障产品运行的安全可靠性,在理论分析的基础上,各行业对k值的影响要素进行了大量试验研究[1-5]。曹增强等[1]采用正交设计试验对航空结构用螺栓氧化、镀锌钝化、镀镉钝化表面处理状态,干摩擦、MoS2油、201油膏润滑条件,2A12、20#钢、30CrMnSiA支撑面材料和螺栓材料、螺栓规格等因素对k值的影响进行了研究,得出润滑条件影响最大,支撑面材料次之,而表面处理状态、螺栓材料、螺栓规格影响较小的结论。曲璇中[2]针对钛合金螺栓表面处理由蓝色阳极氧化改为涂覆MoS2固体润滑剂,研究了表面处理状态变化对扭矩系数的影响,得出涂覆MoS2的扭矩系数仅为蓝色阳极氧化的40%,且一致性更好的结论。贾贤安等[3]对同一批螺栓的螺距、牙型半角、表面粗糙度、螺纹中径制造偏差对k值的影响进行了试验研究,得出螺纹牙型表面质量对k值影响最大,粗糙度每提高一个等级,k值减小0.03左右的结论。
其二是螺栓相对刚度系数(kc)。 外载荷作用下螺栓的剩余预紧力和强度与kc有关,反映了螺栓拉伸刚度和被连接件压缩刚度的占比,大小与螺栓和被连接件材料、连接结构及载荷作用位置有关。工程上一般根据经验选取或通过螺栓拉伸刚度和被连接件压缩刚度近似计算得到,但准确度并不高。许多书籍、手册、标准给出的刚度计算方法也存在一定的差异:如螺栓拉伸刚度计算方法,美国罗伯特·诺顿著的 《机械设计》[6]只考虑了夹紧部分的贡献;德国标准VDI2230[7]考虑了夹紧部分的贡献和螺栓头、螺纹旋合部分的影响;我国 《航天紧固件实用手册》[8]考虑了夹紧部分的贡献及螺纹旋合部分的影响。而被连接的刚度计算更为困难,应考虑各层被连接件的变形协调,确定受压影响区并作等效处理和近似估算。因此,对重要的连接结构kc也需要通过试验测定。
此外,螺栓预紧过程中,存在预紧力矩产生的扭转应力τn=0.5σ0(σ0为预紧力产生的拉伸应力);螺纹强度计算时,存在螺纹扣数取n=3等经验近似计算情况。
这些近似是否合理?采用仿真分析手段能否更准确地解决这些近似问题?为此,本文应用Abaqus有限元分析软件,采用单螺栓连接算例,建立考虑螺纹细节的精细模型,对螺栓预紧受力进行了仿真分析研究。研究了摩擦系数、支撑结构材料对扭拉关系的影响,预紧过程中螺栓的应力和变形、螺纹扣间的受力分配情况等,总结出基于仿真的螺栓相对刚度系数精确计算方法。与理论计算、工程经验和试验调查情况进行对比,得出结论并提出建议,供预紧力设计控制时参考。
1 扭拉关系理论基础
螺栓预紧时由于预紧力矩M 的作用,使螺纹连接件与被连接件之间产生预紧力P0,两者之间的关系为:

式中,k为扭矩系数,d为螺纹公称直径。
预紧转动时,预紧力矩用于克服预紧力作用下螺纹副间正压力、摩擦力产生的力矩M1和螺母与支撑面之间摩擦产生的力矩M2。
对于M1,螺纹副是围绕在一个圆柱体上的螺旋结构,本质是一个斜面,用一个方块表示在螺纹面向上滑动的螺母,预紧时的受力如图1所示[6]。

图1 螺母在螺纹面上的受力分析Fig.1 The force analysis of the nut on the thread surface
根据受力平衡方程,螺纹副间的力矩M1为:
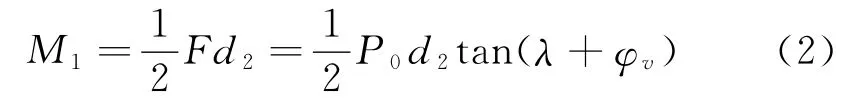
式中,d2为螺纹中径为螺纹升角,p为螺距;为螺纹副当量摩擦角,f1为螺纹副摩擦系数,α为螺纹牙型半角。螺母与支撑面摩擦力矩M2为:
式中,d0为螺纹孔直径或垫圈内径,D0为螺母支撑面或垫圈的外径,f2为螺母与支撑面摩擦系数。
由式 (2)、式 (3)可得扭矩系数k为:
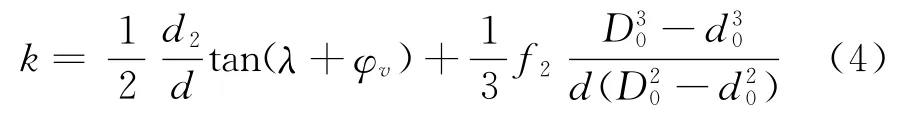
式 (4)反应了扭矩系数与螺栓连接的各种结构参数、螺纹要素及接合面质量间的关系。
2 算例设计
仿真分析难以直接模拟接合面表面的粗糙度、镀层和润滑状态,只能和理论方法一样,考虑结构参数、配合关系和摩擦系数的影响。
由式 (4)可知,当结构参数、螺纹要素固定,扭矩系数主要与旋转面摩擦系数有关。为了和理论分析结果对比,仿真分析以单个螺栓连接为对象,设计了如图2所示的算例。其中螺栓材料为GH4169,螺母材料为30CrMnSiA,螺纹规格为M16×1.5mm,螺栓头和螺母直径为ф24mm,啮合螺纹扣数为7扣。为研究支撑结构材料的影响,被连接件考虑了2A14和30CrMnSiA两种材料。

图2 算例三维图Fig.2 Three dimensional model of the calculation
3 有限元建模
考虑螺纹细节的精细化建模技术是连接螺栓预紧仿真分析的基础。由于螺纹的螺旋特性,很难建立单个螺栓、螺母完全一体的六面体网格模型,需要采用一定的粘接手段。何竞飞等[9]提出了利用螺纹轮廓数学表达式得到精确的螺纹螺旋几何参数,在此基础上利用软件建模功能可实现六面体网格模型。图3是按照此方法得到的螺纹部分网格,因每层几何截面之间存在一定的扭转角,立体上看网格单元没有完整保留螺纹牙顶、牙侧、牙底各部分牙型面,有一些扭曲,需要考虑螺纹副之间接触时会影响接触面的求解收敛,导致分析结果不准确。
本文探讨了采用一定粘接手段的六面体网格建模方法,发现螺牙和螺杆部分粘接会造成各螺纹扣边界刚度的不一致,导致分析结果不准确。为避免这一点,采用了如图4所示的螺纹单独划分网格,完全粘接在螺杆上的全粘接建模方式。因研究的问题与螺纹圆角关系不大,模型中没有考虑圆角。

图3 基于螺纹轮廓表达式建立的六面体网格模型Fig.3 A hexahedral mesh model based on the expression of the thread contour

图4 采用粘接建立的六面体网格模型Fig.4 A hexahedral mesh model based on bonding
固定螺栓头,在螺母上施加载荷。为便于收敛,载荷形式采用扭转角度控制方法,在螺母上施加22.5°的转角。根据螺栓预紧过程中实际可能发生的接触关系,考虑了螺纹副一侧螺牙的接触及螺母对螺栓螺纹、螺栓对螺母螺纹的接触约束和螺母与支撑面的接触。
4 仿真分析研究
4.1 摩擦系数对扭矩系数的影响研究
对不同摩擦系数的预紧受力进行了分析,获得扭矩系数和理论计算结果对比。
分析了被连接材料为2A14,螺纹副摩擦系数f1分别为0.1、0.2、0.4,螺母与支撑面摩擦系数f2分别为0.1、0.2、0.4共9种组合工况下的螺栓预紧受力情况。提取约束扭转力矩作为施加在螺母上的预紧力矩M,螺栓光杆部分横截面的轴向力作为螺栓预紧力P0,根据k=M/(dP0)计算扭矩系数。各工况的分析结果见表1,表中还列出了螺栓光杆部分横截面的扭转力矩M1、螺栓沿轴向位移U2,供后续分析使用。
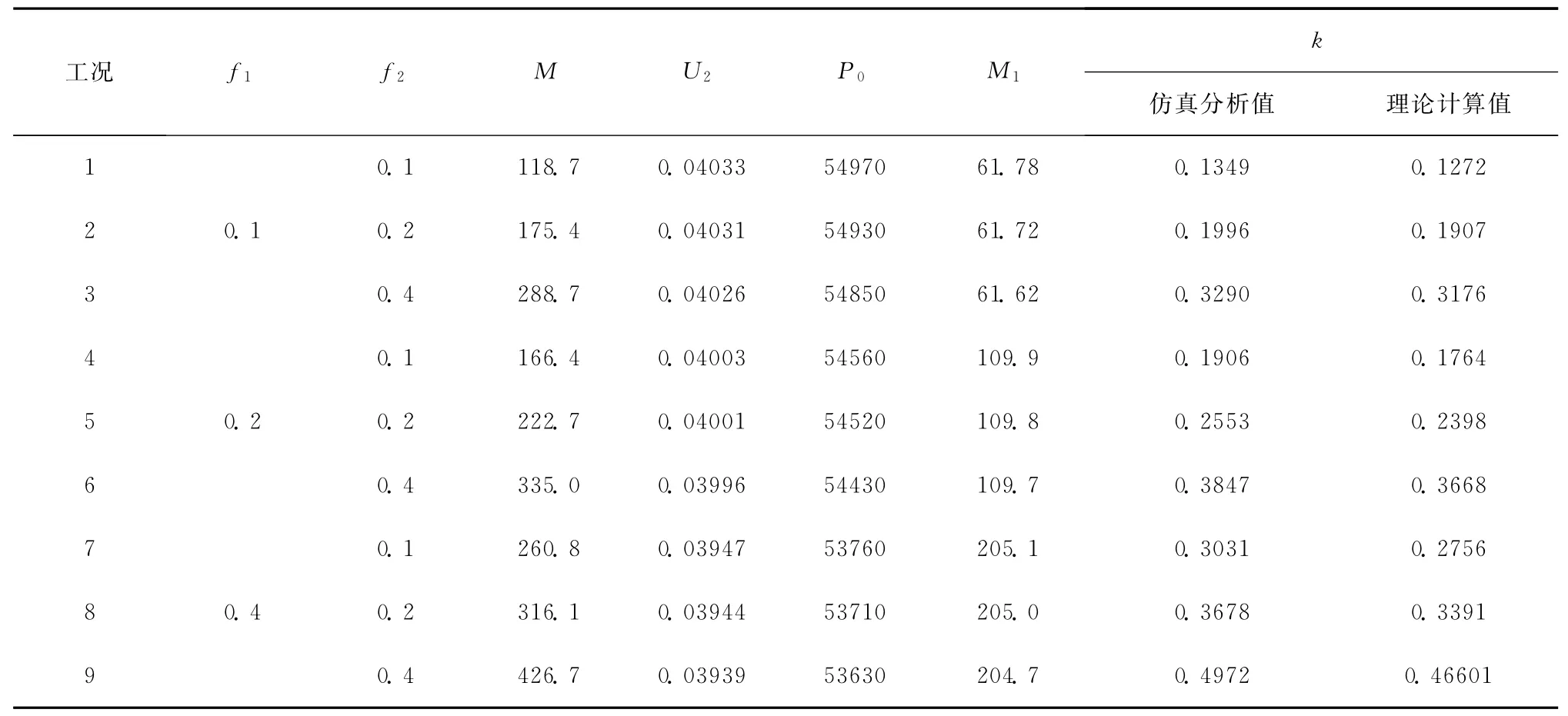
表1 不同摩擦系数结果对比Tab.1 Comparisons of the results of different friction coefficients
对螺母旋转相同角度,所有工况下螺栓轴向伸长量U2基本不变,因此产生的螺栓预紧力也基本相同。摩擦系数不同,旋转相同角度需要克服的扭转力矩不同,因此扭矩系数也不同。图5为f1不变,k随f2变化的仿真和理论计算结果对比曲线。图6为f2不变,k随f1变化的对比曲线。k与f1、f2为线性正比例关系。仿真分析和理论计算的k值结果吻合,仿真值略大于理论值,最大偏差为10%。摩擦系数的影响研究验证了仿真分析结果的有效性和可靠性。
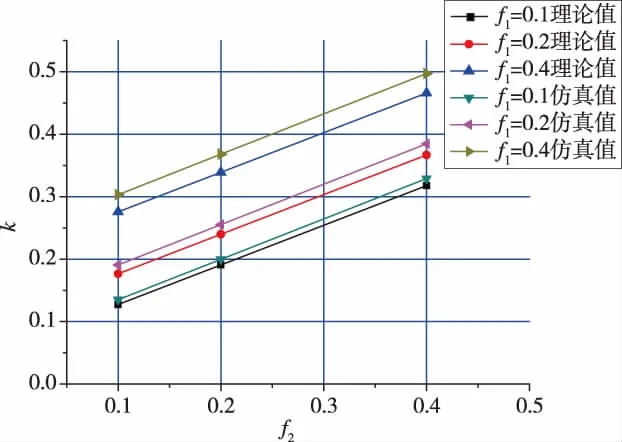
图5 f1不变,理论和仿真的k随f2的变化比较Fig.5 With f1fixed,comparisons of k with f2change curves between theory and simulation

图6 f2不变,理论和仿真的k值随f1的变化曲线比较Fig.6 With f2fixed,comparisons of k with f1change curves between theory and simulation
4.2 支撑结构材料对扭矩系数的影响研究
分析了被连接件材料改为30CrMnSiA,摩擦系数f1=f2=0.1和分别为f1=0.1、f2=0.2时的预紧过程受力,并与材料为2A14的结果进行对比,结果见表2。
扭转相同角度螺栓和螺母的相对运动总量一定,被连接件刚度增大,压缩量变小,因而螺栓的伸长量增长,产生的预紧力增大。从结果看,支撑结构材料对扭矩系数的影响不是很明显,铝合金支撑的k值比合金钢的稍大,且影响效应大小与f2呈正比例关系;这与曹增强等[1]得出的2A12垫圈支撑的螺栓k值大于30CrMiSiA垫圈的结论一致,但比试验得到的影响效应要小。这是因为实际产品即使接合面状态一致,仍存在各种随机性和粘着磨损等其他影响因素,而仿真只能模拟材料刚度变化的影响。
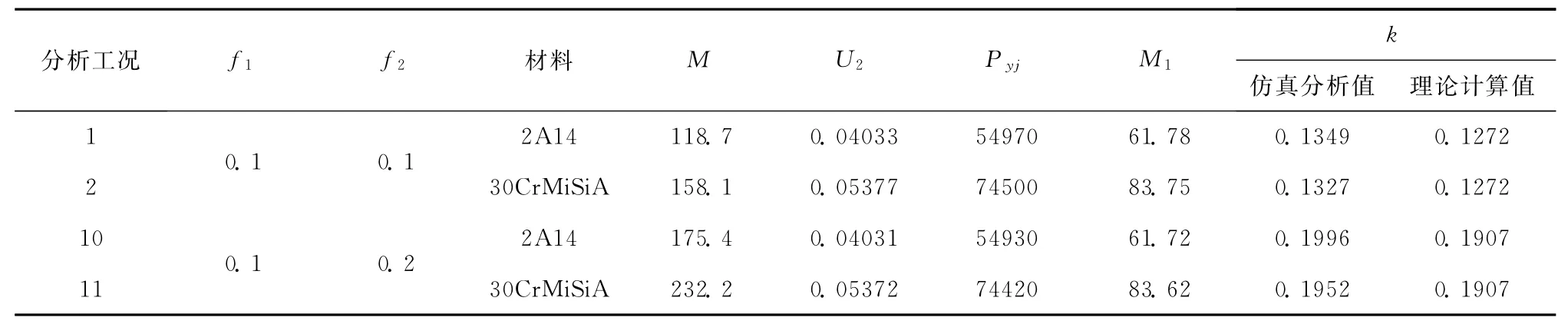
表2 不同支撑材料结果对比Tab.2 Comparisons of the results of different support materials
4.3 螺栓上的扭转剪应力计算
预紧过程中,螺栓在承受预紧力的同时还承受一定的扭转力矩。根据表1中的仿真数据,螺栓承受的扭转力矩大小仅与摩擦系数f1有关,定义M1与总力矩M的比值为km,比较仿真分析与理论计算的km(见图7),两者吻合得很好,仿真分析值略小于理论计算值,最大偏差为6.4%。
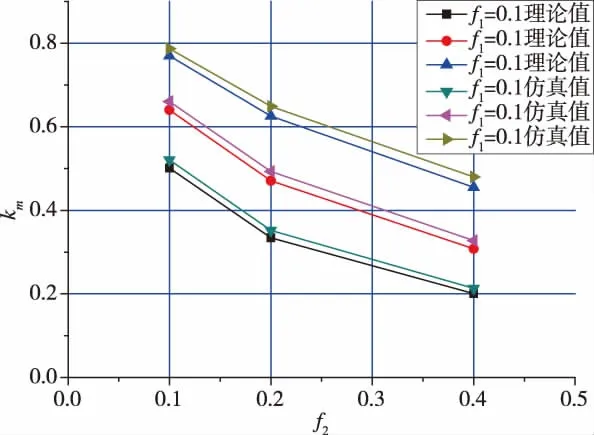
图7 f1不变,理论和仿真的km随f2的变化曲线比较Fig.7 With f1fixed,comparisons of the theoretical and simulated kmcurves changing with f2
设计的螺栓预紧力相同,若f1不同,需要施加的预紧力矩不同,螺栓承受的扭转力矩和产生的扭转剪应力也不同。根据定义,螺栓上的扭转力矩可记为:
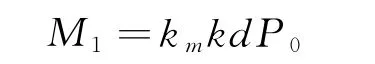
则产生的最大扭转剪应力为:

式中,σ0=4P0/πd2为预紧力产生的拉伸应力。
根据仿真结果,当f1=0.4时,τn可达到(0.85~0.95)σ0,经验公式τn=0.5σ0覆盖不了所有情况。实际上,可通过理论公式(2)准确计算出M1和P0的关系,再准确计算出τn。
工程应用中,给螺栓施加预紧力矩有时会发生螺栓拧断的现象,这往往是因为摩擦系数大于预期,扭转力矩产生的剪应力大大降低了螺栓的拧断拉力。曲璇中[2]得到钛合金螺栓蓝色阳极氧化的拧断拉力只有纯拉伸破坏值的38.3%~61%,涂覆MoS2固体润滑剂的只有60%~86%。因此,实际应用中当摩擦系数大于0.2时,建议采取润滑措施,降低摩擦系数,减小扭转应力,防止拧紧破坏。
4.4 螺纹扣间的受力分配
分析预紧过程中每扣螺纹受力大小,从螺母与支撑面接触端数起,第1扣啮合螺纹用1表示,依此类推,共7扣,并比较每扣螺纹受力Pi占P0的百分比,如图8所示。
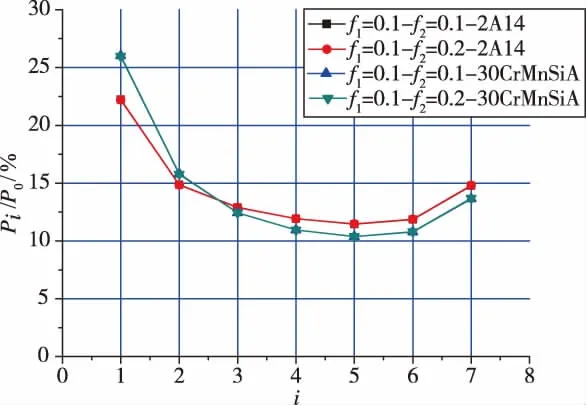
图8 螺纹扣的受力分配曲线Fig.8 Force distribution curves of threads
结构材料相同时,摩擦系数变化,每扣螺纹间的受力分配不变。第1扣螺纹受力最大,其次为第2扣和最后一扣。螺纹扣的受力分配与被连接件材料刚度有一定关系,刚度增大后,不均性增加。算例中,被连接件材料为2A14和30CrMnSiA时,第一扣螺栓承受的载荷分别达到总载荷的22%和26% ,与利津等[10]提供的最大能达到总载荷的30%数据相当;并与校核螺纹剪切强度时,考虑螺纹扣间受力的不均匀性取螺纹扣数n=3也基本一致。
4.5 连接螺栓相对刚度系数计算
预紧力设计时,螺栓预紧后受到外载荷作用,一般根据式 (6)确定螺栓剩余预紧力P,式(7)确定螺栓受到的总拉力P∑(P>0):
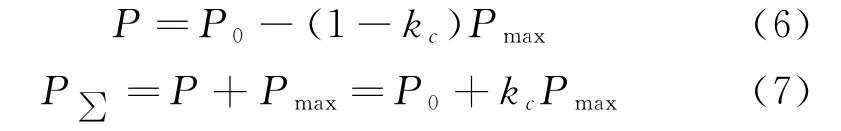
式中,Pmax为外载荷作用下的螺栓最大拉力,kc为螺栓相对刚度系数。
kc的大小与螺栓和被连接件的材料、结构和外载荷作用位置有关,工程上一般根据经验选取或按式 (8)计算:

式中,CL、CF分别为螺栓的拉伸刚度和被连接件的压缩刚度,由于连接关系的复杂和边界的非线性,两者准确计算比较困难,只能做等效近似计算,对重要连接需通过试验测定。
而根据仿真分析结果,可实时计算螺栓相对刚度系数,具体过程如下:
1)根据螺栓承受的预紧力Pyj和伸长量U2计算螺栓的刚度:CL=Pyj/U2;
2)根据扭转角度θ,计算螺栓和螺母的相对运动总量U=θp/360,从而可以确定被连接件压缩量U1=U-U2,再根据预紧力和压缩量便可计算被连接件的刚度CF=Pyj/U1;
3)从而可以计算螺栓相对刚度系数:

仿真和根据近似方法计算的螺栓相对刚度对比见表3,近似计算结果偏大,最大偏差达14.4%。
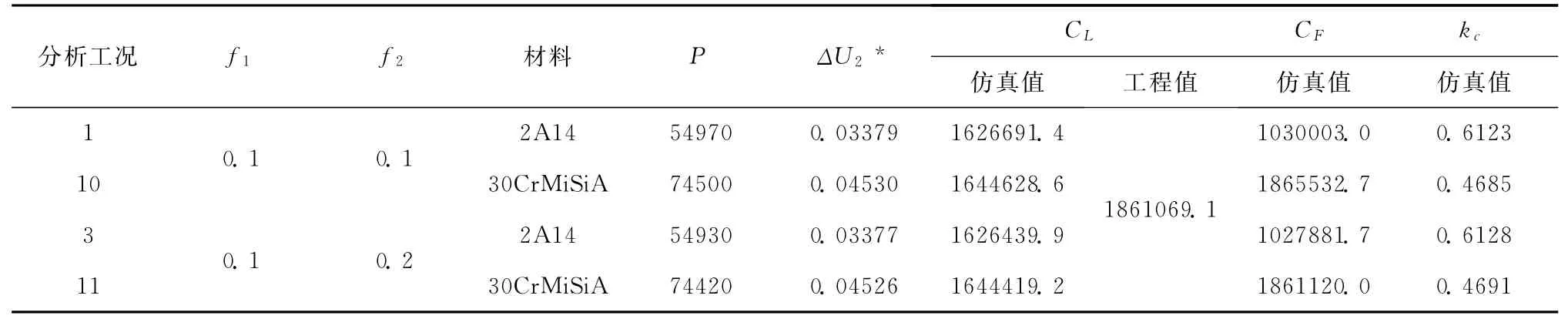
表3 理论和仿真的螺栓相对刚度系数对比Tab.3 Comparisons of relative stiffness coefficients of bolt in theory and simulation
图9是预紧过程螺栓沿轴向变形斜率,除螺栓头由于直径大变形小外,从螺纹旋合中部位置开始由于边界的变化变形也逐渐变小。
4.6 仿真分析结论
通过摩擦系数和支撑面材料对扭矩系数的影响仿真分析及对预紧过程中螺栓的受力、变形规律分析研究,以及与理论计算、试验、经验公式计算的对比研究,验证了仿真分析结果的有效性和可靠性,并得出如下结论:
1)摩擦系数是影响扭矩系数大小的主要因素,对于普通螺纹,扭矩系数和摩擦系数成线性正比例关系。仿真分析结果与理论计算结果一致性较好。

图9 螺栓沿轴向变形斜率Fig.9 Axial deformation slopes of bolt
2)支撑结构材料对扭矩系数影响不明显,铝合金支撑的扭矩系数略高于合金钢。
3)螺栓预紧过程中,当螺纹副摩擦系数较大(>0.2)时,扭转力矩产生的剪应力近似计算公式τn=0.5σ0,不能覆盖螺栓真实承受的扭转剪应力。为降低扭矩剪应力的影响,摩擦系数较大时,应采取润滑措施减小摩擦。
4)预紧力作用下,各螺纹扣之间的受力分配不均,且不均匀性与支撑结构材料有关,材料越刚硬,不均匀性越高。受力最大的为靠近螺母支撑面的第一扣旋合螺纹,最大能达到螺栓预紧力的近30%,螺纹强度设计时,应充分考虑这种受力的不均匀性。
5)根据连接和被连接件的仿真变形结果能获得连接螺栓相对刚度系数,采用此手段对典型连接结构预紧过程仿真可进一步修正螺栓相对刚度系数经验计算公式,获得更准确的结果。
5 综合结论与展望
本文针对现阶段螺栓预紧力设计主要依靠经验近似设计方法,准确度不高,重要连接需要依靠试验的问题,采用考虑螺纹细节的精细化有限元模型对连接螺栓预紧受力进行了系统仿真分析研究。结果表明,在已知摩擦系数的前提下,采用考虑螺纹细节的仿真分析模型能准确模拟连接螺栓预紧受力过程,预示预紧力矩作用下产生的螺栓预紧力及螺栓受力、变形情况,获得扭矩系数、螺栓相对刚度等预紧力关键设计参数,并对螺栓预紧强度进行校核。
仿真分析方法也有一定的局限性,难以直接考虑接合面表面粗糙度、镀层、润滑及表面间的粘着影响等因素,工程中还应采用仿真与测试性试验相结合的方法,用简单的单螺栓试验获得接合面摩擦系数、修正仿真分析模型,提高分析结果可靠性,进一步采用仿真手段对偏心夹紧、偏心加载、多层不同材料、带密封面等复杂受力、复杂连接结构的预紧受力问题进行优化设计和强度校核,可显著提高连接设计效率和可靠性。

