基于力法的超静定捆绑火箭传力特性研究
王 月,冯韶伟,吴 洁,姜 沂,王 君
(1.中国运载火箭技术研究院研究发展中心,北京100076;2.北京宇航系统工程研究所,北京100076)
0 引言
在运载火箭芯级周围捆绑助推器可以有效提高运载能力[1],为保证助推器的可靠连接,通常在助推器的前、后合适部位设置不同的捆绑联接装置,限制助推器的空间六自由度运动,形成静定捆绑连接形式[2]。助推器与芯级之间的捆绑连接是运载火箭设计中的关键。
增加助推器推进剂的有效加注空间是提高捆绑火箭运载能力的有效途径之一,基于制造工艺水平,在助推器直径不变的情况下可以通过增大助推器长度实现[3]。但该措施由于增大助推器长径比,降低了结构的整体刚度,助推器呈现明显的局部模态,在飞行过程中,助推器与芯级之间的距离受到助推器弹性效应的影响而发生变化,这将出现助推器局部低频密集模态的问题,对飞行的安全性产生一定影响。为此,在前、后捆绑间安装一套中捆绑联接装置,从而提高助推器与芯级之间的连接刚度,构成超静定捆绑火箭[4]。
火箭捆绑载荷的精确预示是一项关键工作,将作为捆绑联接装置方案选型、结构设计和强度校核的依据,也是结构精确设计和优化的基础。对于传统的静定捆绑火箭,捆绑联接装置的载荷可以通过力和力矩的平衡方程组进行求解;而超静定捆绑火箭捆绑载荷未知量的个数大于平衡方程组的个数,必须通过引入变形协调条件联立后求解。另外,超静定体系下的传力特性受到捆绑装置布局、结构刚度匹配、装配偏差等多种因素的影响[5],大幅增加了传力特性求解的难度。
本文以某具有较大长径比助推器的超静定捆绑运载火箭为研究背景,基于力法开展超静定捆绑火箭的传力特性分析,研究捆绑装置刚度、捆绑装置安装位置、倾角及捆绑个数对捆绑载荷的影响规律,为工程应用提供理论支撑和参考依据。
1 基于力法的超静定捆绑火箭传力特性研究
1.1 超静定捆绑火箭力学分析模型
以单枚超静定捆绑火箭为研究对象,见图1。定义助推器随动局部坐标系Oxyz,原点O位于助推器头锥顶点,Ox轴沿助推器轴线指向助推器尾端,Oz、Oy轴位于助推器径向平面内,助推器在工作过程中主要受到的作用力包括过载、气动力、操纵载荷、发动机推力以及贮箱晃动力等,助推器仅受前、中、后3个捆绑联接点约束,3套捆绑装置将助推器分为4段,每段长度分别为D0、D1、D2和D3, 前、中捆绑连杆的受力分别为N1~N6,后捆绑装置受力为N9~N11,假设各载荷以图1所示的方向为正。
根据力和力矩的平衡原理,对后捆绑球头取矩,可列写如下6个方程:

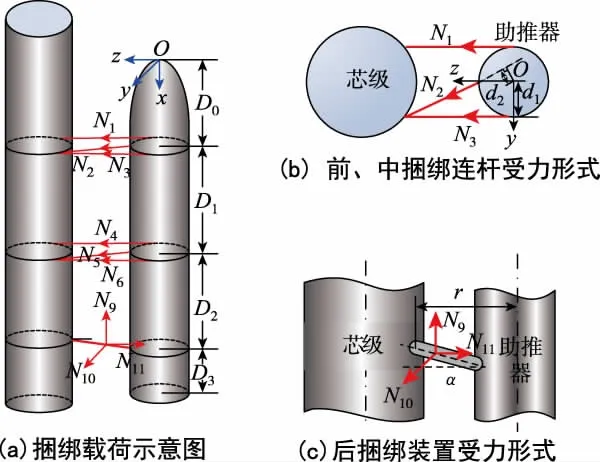
图1 捆绑联接装置的受力图Fig.1 Schematic figure of the booster ′s mechanical analysis
其中,P为助推器发动机传递给芯级的有效推力与助推器自身重力的合力,为助推器在y、z方向上所受外力的合力,Mx、My和Mz分别为外载沿助推器Ox、Oz、Oy轴产生的弯矩。超静定体系中共包含9个未知力,为满足求解条件,需要增加变形协调条件。
1.2 传力特性分析
力法是计算超静定结构的最常用方法,其基本思想是通过去掉多余约束,将超静定结构拆分成静定结构 (称为基本体系[6]),在变形一致性的基础上,利用基本体系的变形条件及连续性条件建立方程,从而再由静定结构过渡到超静定结构[7]。超静定捆绑火箭传力特性影响因素较为复杂,为满足理论分析条件,做如下简化和假设:
1)假设芯级与助推器变形协调,即捆绑装置与芯级相连处为固定约束;
2)假设助推器为均质结构,可以由均匀截面的梁模拟。
取xOz平面内进行传力特性分析,由于后捆绑装置主要用于传递沿Ox轴的轴向载荷,前、中捆绑连杆只传递沿Oz轴的径向和沿Oy轴的横向载荷,因此在平面内,后捆绑约束x向和z向位移,前、中捆绑装置只约束z向位移,其传力模型为具有一次超静定的多跨梁,简化力学模型见图2。

图2 平面助推器简化力学模型Fig.2 The simple model of the booster in xOz plane
助推器总长为L,弹性模量为E,惯性矩为I,助推器轴线与后捆绑球头的距离为r(见图1(c));在径向平面内,直连杆与助推器轴线间的距离为d1,斜连杆与助推器轴线间的距离为d2(见图1(b))。R1、R2、R3分别为前、中、后捆绑装置的z向载荷,R3x为后捆绑轴向载荷。将P移动到后捆绑的水平位置,同时需增加等效弯矩M,M=P·r;气动力分布函数为fx();操纵力的z向分量RC作用在助推器末端[8];助推器氧箱和燃箱液体晃动载荷[9]分别为FH1、FH2,距离助推器顶点LH1、LH2,且满足:

由于捆绑装置刚度并非无限大,因此在实际工作过程中会产生变形,设前、中、后捆绑沿z向的等效刚度分别为Gz1、Gz2和Gz3, 并具有拉压不同刚度特性。支座在相应方向上的变形满足:

设中捆绑z向载荷R2为多余约束,建立基本体系,在单位载荷作用下,弯矩函数为:

可以计算出前捆绑的变形量:


在静定体系下,由后捆绑点的力矩平衡方程可以求得:
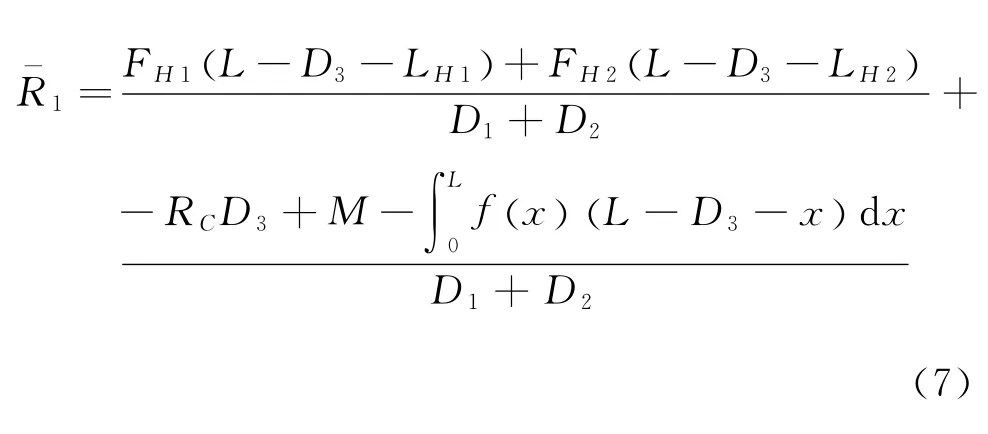
因此MP满足:

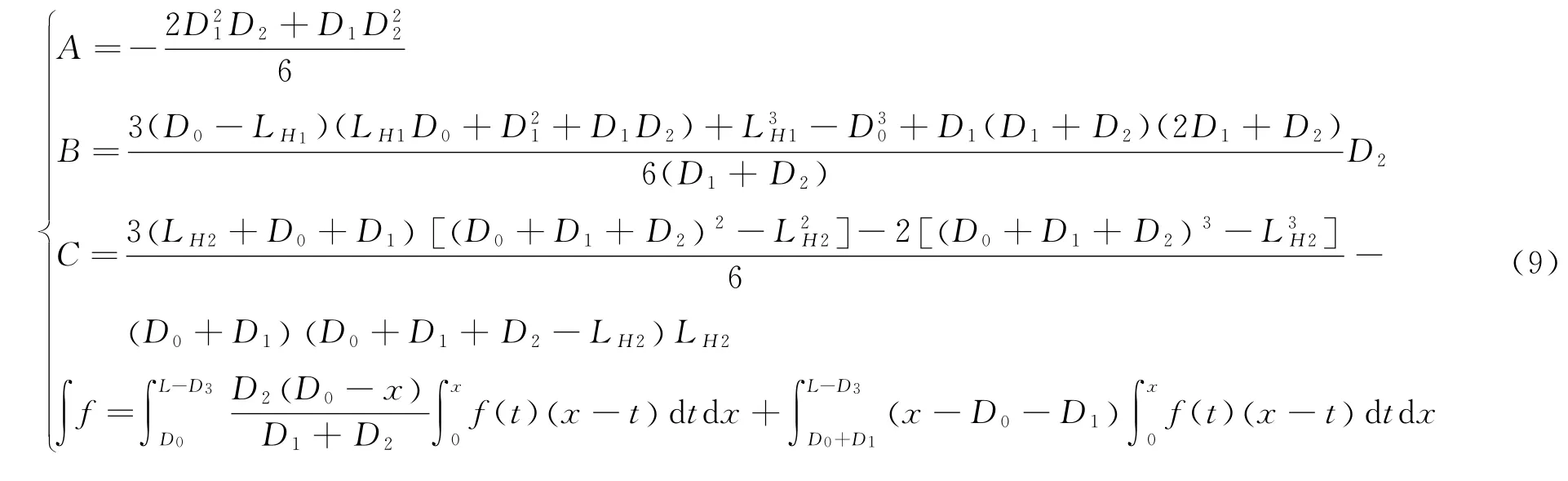
此时力法方程为:

从而可以计算出:


以竖立加注状态为研究对象,此时P为助推器的重力,方向沿助推器轴向指向助推器尾端,将解析计算结果分别与忽略捆绑装置变形情况(令Gzi=∞,i=1,2,3)的计算结果、工程有限元计算结果进行比较,多余约束在xOz平面的合力R2的计算结果见表1。
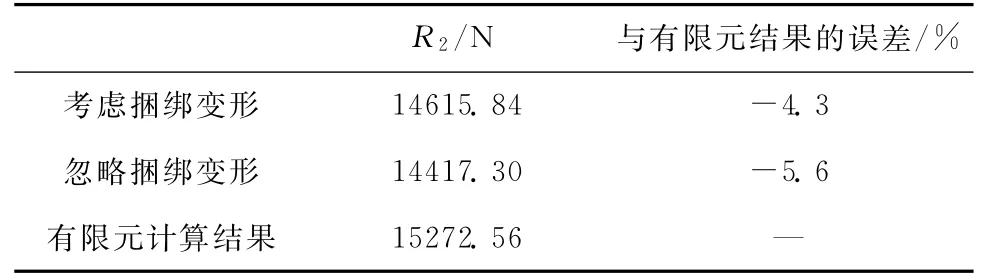
表1 3种计算方法的结果比较Tab.1 The result of three methods
计算结果表明:在竖立加注状态下,3种计算方法所得的结果相近,相比于忽略捆绑装置变形的方法,本文计算结果与有限元结果更接近,误差为4.3%。
2 超静定捆绑载荷影响分析
上述分析表明,超静定捆绑火箭的捆绑装置内力不仅与外载分布有关,还与各捆绑装置和助推器本身刚度之间的比值、捆绑位置及捆绑个数有关。
2.1 捆绑装置刚度对捆绑载荷的影响分析
分别改变前、中、后各捆绑装置的刚度,各捆绑装置刚度与原模型自身刚度的比值与R2的关系曲线,如图3所示。

图3 捆绑装置刚度比值与R2载荷关系曲线Fig.3 Relation between R2and stiffness ratio
对于中捆绑载荷来说,降低前捆绑装置刚度、增大中捆绑及后捆绑装置的刚度都会减小载荷的幅值;相比于增加捆绑装置刚度,降低捆绑装置刚度、降低对R2载荷影响更显著。以中捆绑刚度为例,当捆绑装置刚度减小为1/10时,R2增大了13.9%;而当捆绑装置刚度增大2倍后,继续增加捆绑装置刚度对载荷影响很小,如刚度增大10倍后,R2仅降低1.2%。这是由于随着捆绑装置刚度增大,支座变形量降低,从而更加接近于表1中忽略捆绑变形的模型,最终趋于统一值。
从图4(a)所示的主效应图中可以定性地看出:增大中捆绑装置刚度对降低载荷的贡献最明显;图4(b)所示的Patero图结果表明:增大中捆绑装置刚度对降低R2载荷的贡献率为63.8%,而增大前捆绑刚度与减小后捆绑刚度的贡献率分别仅为16.9%和14.7%。

图4 各捆绑装置刚度对载荷的影响图Fig.4 The influence of the load by the linkages ′stiffness
结果表明,增大捆绑装置的刚度能够一定程度上降低自身捆绑载荷的绝对值。
2.2 捆绑位置对捆绑载荷的影响分析
研究表明,在振型的波腹点处增加约束对提高全箭固有频率的效果最佳[10]。但在实际工程中,捆绑面位置的设置必须结合火箭结构特点。对于液体运载火箭来说,其箭体结构由推进剂贮箱和蒙皮桁条壳体结构组成,其中贮箱箱体柱段厚度仅有1mm~3mm,不仅刚度较弱,无法承受捆绑装置传递的集中载荷,而且对贮箱结构的局部加强将导致结构质量大幅增加、贮箱承载复杂等问题,因此捆绑面应设置在蒙皮桁条壳体中易于加强的部位。
忽略除助推器推力以外的所有外力,按照1.2节的方法,在xOz平面内前、中、后捆绑的载荷为:
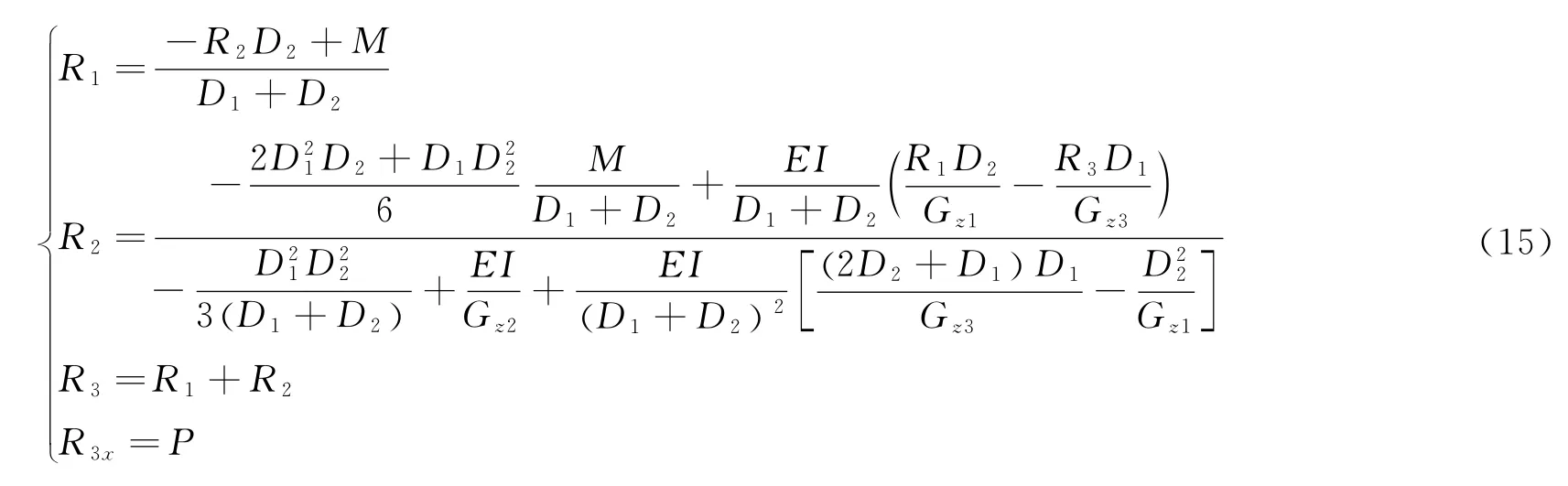

在保证结构尺寸与支撑形式不变的前提下,选取前、中、后捆绑联接装置安装位置,以及球头栓轴线与水平面夹角α′作为变量,研究各变量对的影响规律,见图5。
结果表明:保持中捆绑点位置不变,当前、后捆绑点与中捆绑点位置接近,距离小于2m时,会急剧增大,其中移动后捆绑的效果更明显;保持前、后捆绑点不变,移动中捆绑点的位置,会随后捆绑点位置的减小而增大,且当二者距离小于2m时,急剧增大。对于主捆绑轴线夹角α′来说,当其取合适的值使=0时,能够较好地改善主捆绑的受力状态。

图5 捆绑位置、安装倾角与的关系曲线Fig.5 The curve of and the location,installation angle
2.3 捆绑个数对捆绑载荷的影响分析
在仅受发动机推力P的情况下,研究捆绑个数对捆绑载荷的影响。当去掉中捆绑连杆,结构变为两捆绑静定模型,其前、后捆绑在xOz平面的内力分别可以通过平衡方程求得。

与超静定捆绑火箭模型相比,前捆绑载荷方向发生了变化,且当D2>2D1时,超静定捆绑火箭的载荷绝对值将大于静定捆绑火箭;对于后捆绑径向载荷来说,超静定捆绑火箭大于静定捆绑火箭。不同捆绑个数下捆绑连杆载荷对比情况如表2所示。

表2 不同捆绑个数下捆绑载荷对比Tab.2 Comparison of the load between different strap-on forms
结果表明,超静定捆绑结构引起了捆绑载荷重新分配,对于前捆绑载荷,连杆由受拉改为受压;对于后捆绑,超静定捆绑的形式增加了装置的径向载荷。由于轴向传力形式不变,因此对轴向载荷几乎无影响。
3 结论
本文基于力法研究超静定捆绑火箭的传力特性,获得了捆绑装置刚度、捆绑装置安装位置及倾角和捆绑个数对捆绑载荷的影响规律,能够为处于方案论证阶段的超静定捆绑火箭提供依据。结论如下:
1)超静定捆绑火箭的捆绑装置内力与捆绑装置刚度和箭体刚度之间的比值有关,增大捆绑装置的刚度能够有效降低捆绑载荷的绝对值;
2)捆绑装置的安装位置虽能够改变捆绑载荷的传力特征,但对箭体动特性、控制系统以及结构设计等多方面影响较大,工程中可以通过调整主捆绑装置轴线夹角改善受力状态;
3)相较于静定捆绑火箭,超静定捆绑引起了捆绑载荷重新分配,其中前捆绑连杆承载状态发生改变,后捆绑径向载荷有所增加。

