弹道导弹发射点位置的弹道重构寻优估计
刘新建,胡佳鑫,杨乐平
(国防科技大学空天科学学院,长沙410073)
0 引言
弹道落点预报是弹道导弹预警和反导中的重要任务,但弹道导弹发射阵地的位置估计在弹道导弹防御中也具有重要作用。对于战略弹道导弹,要准确判定是哪个敌对国家进行的攻击,何时何地发射的,以便迅速进行反击;对于战术弹道导弹,由于发射也需要调平和方位瞄准,一般是事先安排了有阵地依托的发射,也要尽可能准确知道敌方是何时何地发射的,以便告知侦察卫星对该区域扫描拍照,通过卫星图像进一步精确锁定坐标,以便轰炸发射阵地或弹道导弹贮存基地。
Danish[1]较早研究了天基测量战术弹道导弹(TBM)主动段弹道的发射点参数估计问题;Isaacson等[2]研究了战术弹道导弹的状态估计和轨迹预报。国内李盾等[3]基于同步轨道预警卫星对助推段弹道导弹的测量信息,利用改进的高斯-牛顿法探讨了发射点参数的最大似然估计,但必须利用主动段目标弹道曲线的先验信息;宋伟等[4]、阳曙光等[5]研究了双星交汇测量战术弹道导弹主动段的弹道参数,并利用多项式拟合进行弹道外推估计发射点参数;王瑞等[6]研究了天基红外低轨卫星系统对自由段空间目标定位的最小二乘、卡尔曼跟踪滤波及自适应滤波的方法。但鲜见基于对大气层外被动段弹道的短弧测量对发射点位置进行估计的研究,而且这种多项式弹道拟合外推发射点的方法较为简单,对TBM主动段可能有效,但对中远程、洲际弹道导弹的被动段测量信息反推发射点未必有效。
发射点的位置确定比弹道的落点预报更难,前者是逆问题;后者是正问题,相对要简单。
本文基于天基或地基设备的被动段短弧测量数据,假设在WGS84系中,得到了来袭弹道导弹大气层外的部分弹道,提出发射阵地位置估计方法。
1 滤波定轨
(1)坐标参数转换
假设ti∶xi,yi,zi,vxi,vyi,vzi(i=1,2,…,n)为弹道导弹在真空中的一段短弧轨迹测量数据,分别从WGS84系转换到某一地心惯性系,如J2000 系,得到ti∶Xi,Yi,Zi,Vxi,Vyi,Vzi。
其中,ti为飞行时刻,Xi、Yi、Zi为弹道导弹在该时刻的3个直角坐标位置分量,Vxi、Vyi、Vzi为该时刻的3个速度分量。
(2)均值滤波去噪
由于每个测量值含有噪声,并非是弹道导弹的真实状态,因此需要去噪滤波。工程上有多种数字滤波方法,如卡尔曼滤波、最小二乘滤波、自适应滤波、平均值滤波。特别对于地基雷达,由于地球曲率的影响,可见弧段极短,而弹道导弹飞行速度极快,获得的测量数据不会很多,因此可采用单点均值滤波。均值滤波最简单,没有延迟,对少量的短弧测量数据鲁棒可靠。
所谓均值滤波,就是依次利用测量数据ti:Xi,Yi,Zi,Vxi,Vyi,Vzi(i=1,2,…,n),根据真空段自由飞行动力学模型式 (2),进行数值积分,获得测量数据段之后任选的定轨时刻tf的n个状态数据。如果测量弧段的数据没有噪声,那么依次积分,预报tf时刻的六分量状态应该是完全相同的;但正因为存在测量噪声,所以依次积分获得该时刻的状态也存在噪声,那么求平均值。

可是tf时刻的弹道导弹真实状态只有一个,如果测量数据的噪声遵循白噪声分布,而且采样点足够多,则平均值逼近真值,就得到了弹道导弹真实状态tf:Xf,Yf,Zf,Vxf,Vyf,Vzf。
(3)根据如下地惯系中空间飞行器的动力学
微分方程组[7]
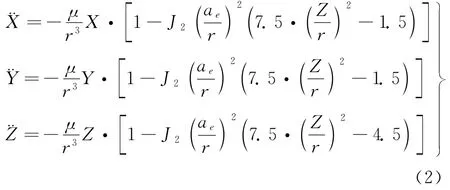
其中,地球扁率J2=1.08263×10-3, 地球引力常数μ =3.986005×1014m3/s2, 地球长半轴=6378140m,地心矢径再由上述定轨点的真实状态,进行弹道积分预报再入落点e的直角坐标位置和速度Xe、Ye、Ze、Vxe、Vye、Vze。
2 发射点初始解析估计
为获得初始估计,不考虑弹道导弹助推段弹道及再入段大气阻力的影响,假设导弹在地面瞬间获得足够能量,满足测量弹道所预报落点的位置和速度要求,不妨称为脉冲发射点。脉冲发射点的位置估计是发射阵地位置的近似估计,是弹道重构寻优估计的基础。

图1 二体脉冲弹道示意图Fig.1 Impulse ballistic sketch of two-body problem
1)如图1所示,根据再入点e的直角坐标和速度Xe、Ye、Ze、Vxe、Vye、Vze, 计算经典轨道根数a、e、i、Ω、ω、M,并求其真近点角fe[8]。
2)求二体脉冲发射点的真近点角fk

于是不难求得其对应的平近点角Mk和偏近点角Ek。
3)求二体飞行时间

其中,a是定轨得到的弹道长半轴,平近点角Me=M。
4)求脉冲发射点的经纬度
理论上,这是一个已知再入终点位置和飞行时间,反求初始点位置的逆向动力学问题。这里提出利用二体运动轨道的封闭性特点,避开逆向积分问题。
根据二体运动理论,二体脉冲发射点的直角坐标有如下解析公式[9]
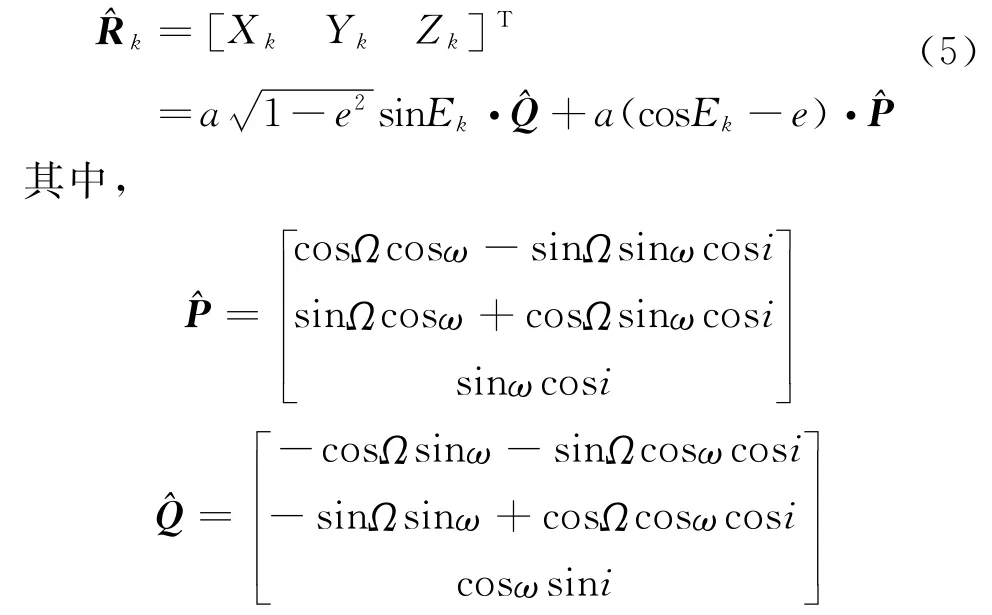
再将其从地惯系转换到WGS84系的xk、yk、zk,由此计算脉冲发射点的经纬度λk、фk,就是发射点的初步估计,误差与主动段的弹道设计程序及参数有关,对于射程超过10000km的洲际弹道导弹,数值仿真表明本方法求得发射点最大误差为200km。
初始解析估计的计算量很小,适合于弹道导弹防御系统实时快速预报,至少能准确告知弹道导弹来自哪个敌对国家。
3 弹道重构寻优估计
由于脉冲点的估计与发射阵地的真实位置存在误差,需要进一步修正。策略是在脉冲发射点附近进行系列弹道重构,仿真模拟弹道导弹从发射点垂直起飞、主动段程序转弯、末级瞄准与闭路控制关机,优选出满足定轨预报再入点约束的重构弹道,输出所对应的发射点经纬度。
3.1 寻优方法
1)以脉冲发射点及对应的自由段飞行时间为中心,设定经纬度误差边界范围,如±2°(对应440km边长的正方形),自由段时间偏差,如±100s,划分三维网格如图2所示,遍历搜索可行解与最优解,发射点位置精度与网格大小有关,显然网格越细,搜索的时间越长。
2)根据脉冲点与再入落点的经纬度,由球面三角公式估计弹道射程。
3)按照射程大小 (洲际、远程、中程、近程和短程),参考对应的国内外典型弹道导弹的参数,虚拟来袭弹道导弹的动力学仿真参数,如级数、各级的推力、质量、秒流量、燃烧时间以及气动阻力、升力系数。
4)按照弹道导弹主动段的弹道设计方法,设计转弯程序如攻角函数、各级转弯角速率[8]。

图2 脉冲发射位置点附近的三维网格Fig.2 Three dimensional grid near impulse launch location
5)为确保再入位置约束,导弹末级采用Lambert制导方法[7],根据末级当前位置矢量,再入落点位置矢量和飞行时间要求,求取需要速度,利用速度增益制导构成闭路关机控制,求得导弹末级飞行的俯仰角、偏航角和关机时间。
3.2 约束条件
以上给出了主要搜索变量的边界约束和方法,但要模拟真实弹道,还需加入弹道重构约束条件,即仿真弹道的再入点位置和速度六分量应与弹道测量后的定轨值相同或逼近。
再入点位置误差约束:Δλ≤ελ,Δφ≤εφ,ΔH ≤εH。
即经度、纬度和高程三分量仿真值与定轨值的误差小于设定值,因为末级采用了Lambert制导方法需要速度闭路制导,仿真会自动满足,简化了位置约束的求解。
再入角度误差约束:ΔΘ≤εΘ,Δσ≤εσ,即速度的倾角和偏角误差小于设定值
3.3 目标函数
取再入速度模的误差ΔVe为目标函数,应取最小。
4 仿真验证
这里以某三级弹道导弹A为例,给出数学仿真予以说明。
(1)导弹A的主要参数[10]
一级起飞质量为34.5t、推力为912kN、工作时间为61s、推进剂秒流量为360kg/s;
二级起飞质量为12t、推力为270kN、工作时间为65s、推进剂秒流量为108kg/s;
三级起飞质量为5t、推力为155kN、工作时间为59s、推进剂秒流量为62kg/s。
末修级工作时间由闭路关机控制指令决定。但弹道数值仿真时,为简化起见,可不设末修级,第三级工作时间不固定,由闭路关机仿真时间决定,只要满足自由段飞行时间约束和落点位置约束就可以。其他中短程的战术弹道导弹类似,也可不设末修级。
(2)发射点和目标点参数假设
发射点:经度-118°,纬度30°;
目标点:经度112°,纬度34°;
两点之间的射程为11643km。
(3)仿真过程
1)在脉冲估计的基础上,编写3自由度仿真优化搜索程序。
2)设计一条从发射点到目标点的标称攻击弹道,获得中段N个短弧采样数据,例如50个轨迹点,每隔1秒一个采样数据,适当加入白噪声,基于这N个数据,完成定轨计算。
3)基于以上方法,完成发射点的二体脉冲估计和弹道重构寻优估计。
(4)仿真结果
二体脉冲估计:
发射点位置误差
经度差:-0.127°(对应14km)
纬度差:1.0015°(对应110km)弹道重构寻优估计:
发射点位置误差
经度差:0.125°(对应14km)
纬度差:0.0015° (对应0.2km)
(5)约束条件逼近度
速度误差:0.047m/s
当地速度倾角误差:0.85°
速度偏角误差:0.027°
经度差:0.0045° (对应0.5km误差)
纬度差:0.0044° (对应0.5km误差)
图3给出了上述数值仿真算例的寻优估计重构弹道。

图3 弹道重构寻优估计数值仿真轨迹示意图Fig.3 Numerical simulation sketch of optimal estimation with trajectory regeneration
可见,对于本算例的二体快速脉冲估计,发射点的位置误差为120km,这对于判断来袭弹道导弹的敌对国家是够用的。而经过弹道重构的寻优估计,发射点位置误差估计降到了15km左右,提高了可观的估计精度,如果发射点寻优网格进一步细分,误差还可能降低。
5 结论
提出的弹道导弹发射参数估计方法包括脉冲初始估计和弹道重构仿真两部分,前者实时性好,也是后者的基础。后者以脉冲点为估计中心,对于战略弹道导弹,以经纬度±2°误差为位置边界,以二体飞行时间tke为中心,±100s为自由段的飞行时间边界,划分三维网格,并以再入点的位置三分量、当地速度倾角、速度偏角共5个弹道重构约束条件,以速度误差为目标函数,进行三自由度弹道控制仿真与优化搜索,求取发射阵地坐标,这样来减小发射点位置估计误差。对于战术弹道导弹,网格边界可通过仿真进一步缩小,方法类似。
这种弹道重构方法,不需要完全一致的弹道导弹参数,只要大致接近就可,因为是按照弹道导弹攻击目标所采用的典型弹道规划方法,基于动力学与控制仿真,并通过优化搜索参数和Lambert末制导来满足再入边界条件的,使得数学仿真弹道能够逼近实际飞行轨迹。
只要获得了来袭弹道测量参数,本方法可以获得较高置信度的估计,在弹道导弹预警和防御中有一定参考价值。

