车辆侧倾状态估计的研究∗

董明明，张 钰，王振峰

(1.北京理工大学机械与车辆学院，北京 100081； 2.天津科技大学机械工程学院，天津 300222)

前言

在车辆行驶过程中，侧倾对乘客的安全性有重要的影响。车辆侧倾或侧翻已被认定为死亡率最高的事故类型。美国国家公路交通安全管理局(NHTSA)调查数据显示[1-3]，虽然由于车辆侧倾引起的死亡人数在过去10年中有所减少，但仍占有很大的一部分比例[2，4]。因此有必要对车辆的侧倾运动进行深入研究，以提高乘客的安全性。

近几年来，对于车辆侧倾运动的研究主要集中在检测系统和预防算法上。文献[5]中根据车辆行驶时的状态估计侧倾角和侧倾率，计算危险指数。文献[6]中利用慢速主动悬架控制的非线性模型，减小了车身摇摆和侧倾倾向。为进一步对车辆运动进行优化控制，须获取车辆实时运动状态。为此，模糊观测器被广泛应用于车辆与悬架的耦合中，使用T-S模糊模型估计车辆的状态，结果表明与参考数据具有较高的一致性[7]，有的文献中还研究了基于磁流变(MR)阻尼器的半主动1/4汽车悬架的观测器[8]。

为进一步提高车辆耦合系统状态估计的精度，本文中提出了利用T-S模糊观测器对车辆侧倾运动进行状态估计，并通过仿真和实验对模型进行了验证。

1 车辆运动学模型

1.1 整车模型建立

为获得车辆行驶时其垂向与横向的运动学关系，构建了整车9自由度模型，如图1所示。

图1 车辆9自由度运动学模型

整车9自由度模型包含车辆的侧倾、俯仰、横摆运动和垂向与横向运动以及4个轮胎的垂直运动。模型中的参数见表1。

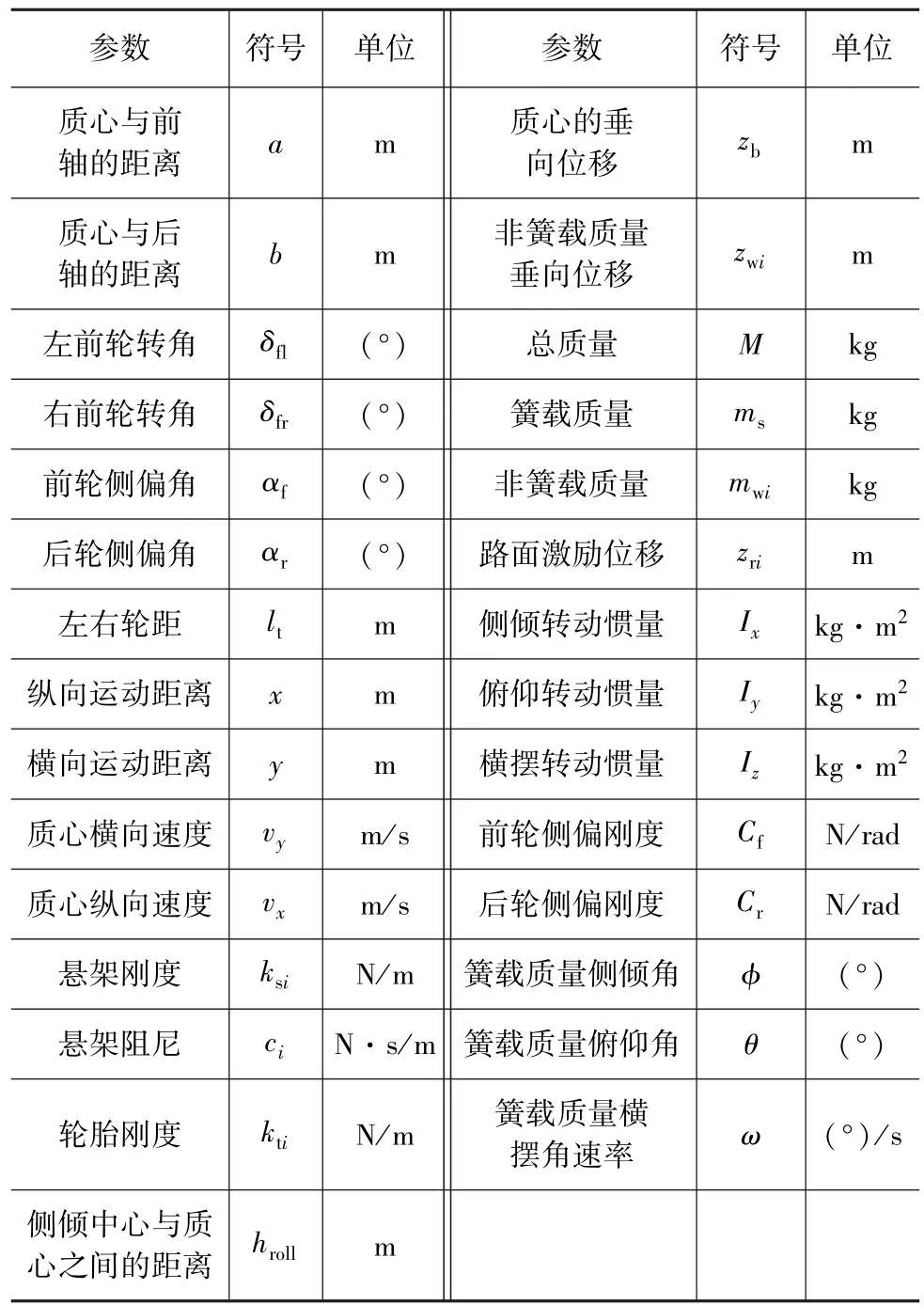
表1 整车9自由度模型符号参数定义

根据牛顿第二定律，整车9自由度模型车身垂向运动的平衡式为

式中：Fs为悬架总作用力；Fsi为第i个悬架的作用力，i＝1，2，3，4 分别为左前、右前、左后和右后悬架。Fsi可由以下公式得到

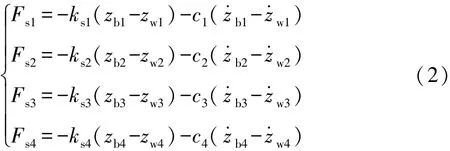
其中

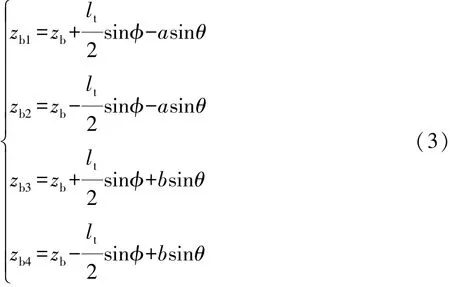
非簧载质量垂向运动方程为

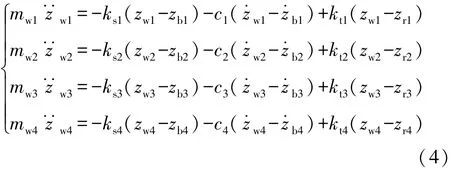
车身的仰俯运动和侧倾运动方程分别为

式中My和Mx分别为车辆的俯仰力矩和侧倾力矩。

车辆横向运动和横摆运动方程为

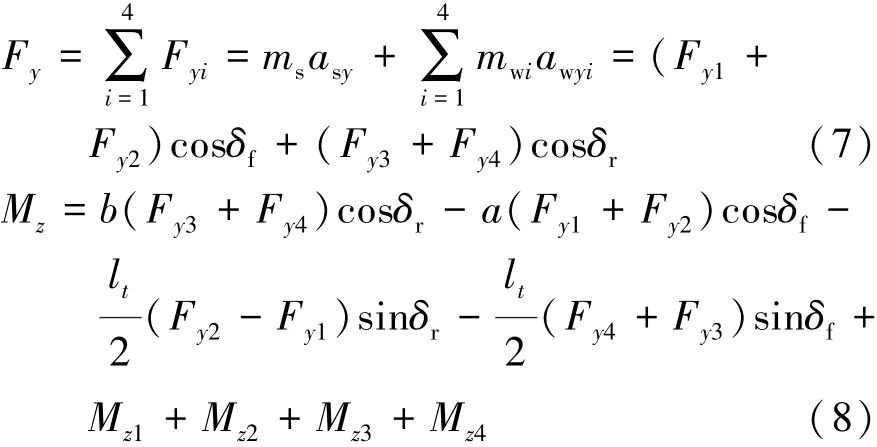
式中Fy和Mz分别为轮胎的横向力和横摆力矩。

1.2 采用T-S模糊方法建立轮胎与整车模型

由Pacejka[2]提出的“魔术公式”被广泛地应用于描述轮胎模型。根据该模型，车辆前后轮胎横向力与侧偏角存在如下关系：

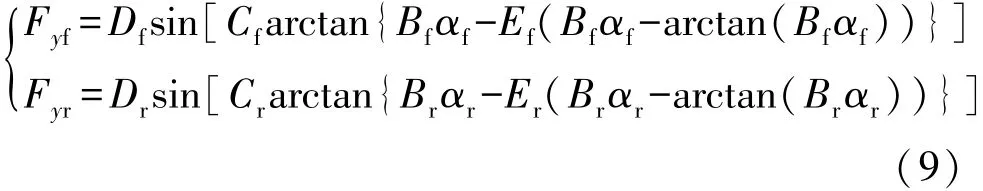
其中

式中各参数见表1。

上述公式需要多种非线性参数，因此在参数未知情况下，模型还不能使用。当侧偏角都很小时，横向力与侧偏角成一定比例，此时模型的线性度较好[7]。由于系统的非线性，利用T-S模糊规则理论结合横向力与侧偏角之间的关系得出：若｜αf｜为Mf1，则 Fyf＝Cf1αf；若｜αf｜为 Mf2，则 Fyf＝Cf2αf；若｜αr｜为 Mr1，则 Fyr＝Cr1αr；若｜αr｜为 Mr2，则 Fyr＝Cr2αr。 其中，Cfi与 Cri为车辆前轮与后轮的侧偏刚度，Mf1与Mr1为前轮与后轮的小侧偏角区域，Mf2与Mr2为前轮与后轮的大侧偏角区域。

综合以上模糊规则，则轮胎的整体横向受力可表达为

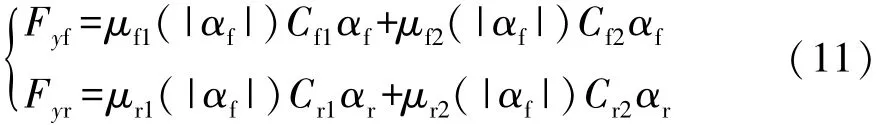
式中 μfi与 μri为属于 Mf2与 Mr2的隶属度函数。 μfi与μri具有以下性质：

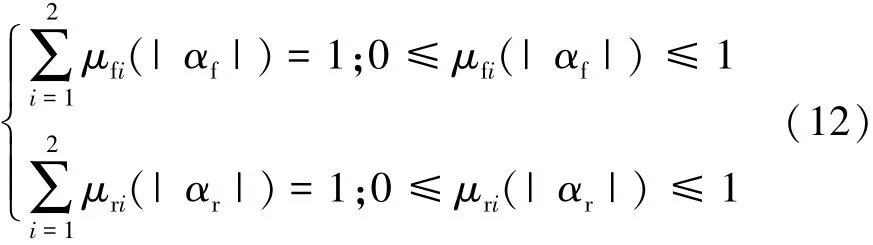
其中

式中 afi，bfi和 cfi(ari，bri，cri)为设置参数，可通过粒子群优化方法得到[9-10]。

利用上述方法将轮胎T-S模型[11-12]与非线性“魔术公式”模型进行对比，结果如图2所示。

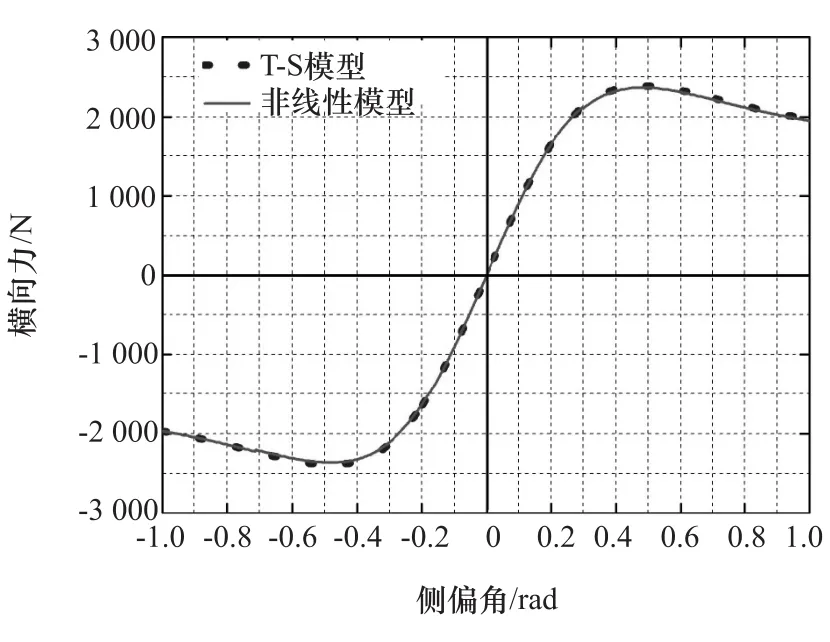
图2 轮胎T-S模型与非线性模型比较

将T-S轮胎模型带入到整车动力学模型中，定义系统状态与输出状态为

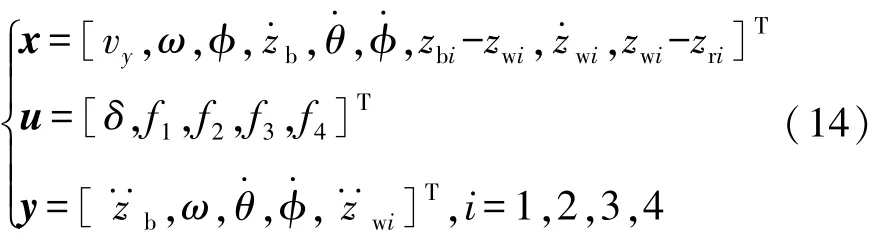
结合状态空间表达式可得

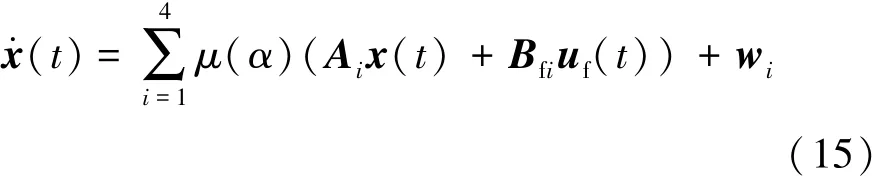
式中：Ai为整车系统矩阵；Bfi为系统输入矩阵。具体表达式见文献[11]。

2 车辆系统T-S模糊观测器设计

2.1 T-S横向运动模糊观测器设计

为得到在路面激励和转向盘转角下的侧倾角和侧倾率，利用T-S模糊模型对其进行了有效估计，具体流程如图3所示。

用于估计侧倾角和侧倾率的T-S模糊观测器公式为

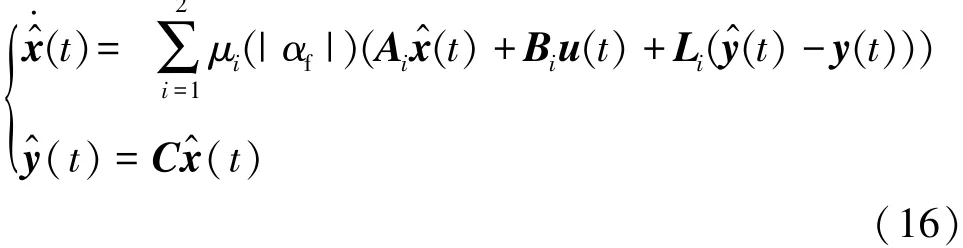
定义状态误差为

对式(17)微分可得

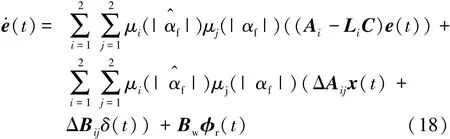
且 ΔAij＝Aj-Ai；ΔBij＝Bj-Bi

此时，定义新的状态变量和系统干扰：

则扩展系统状态与系统估计误差为

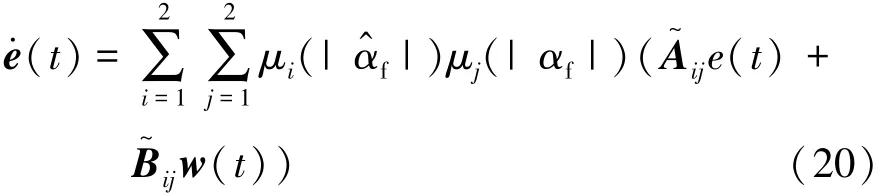
其中

此处需要说明的是，系统干扰项w(t)主要由转角与路面激励组成，由于其自身特性限制故可近似认为w(t)是能量有界输入。

由以上分析可知，在考虑路面不平度与转角不确定工况下对估计状态误差影响时，须有效计算获取T-S观测器增益Li。其中一种有效解决方法是：使由误差干扰到状态估计所诱发的误差增益L2(H∞范数)最小[12-13]。此误差增益L2与在向量w(t)和估计误差e(t)之间的关系为

通过合理定义最小上界与误差增益L2，式(22)可描述为

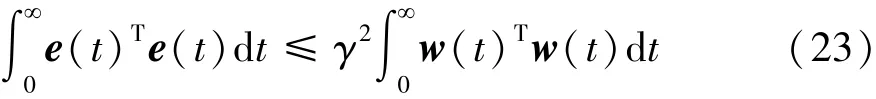
若存在正定对称矩阵P1与P2，且矩阵Mj与正定维数ξ满足以下LMI不等式：

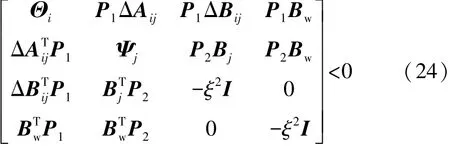
其中

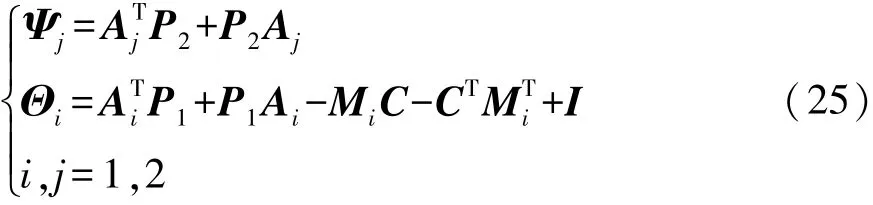
当式(17)的估计误差逐渐趋于零，且满足式(23)，便可得T-S观测器增益Li的最优解，即Li＝M。关于轮胎T-S观测器增益求解的更多论述，可参看文献[12-14]。

2.2 T-S垂向运动模糊观测器设计

假设可得到簧载质量和非簧载质量的加速度作为实际测量输出的结果。根据这些结果，T-S模糊观测器按照如下设计：

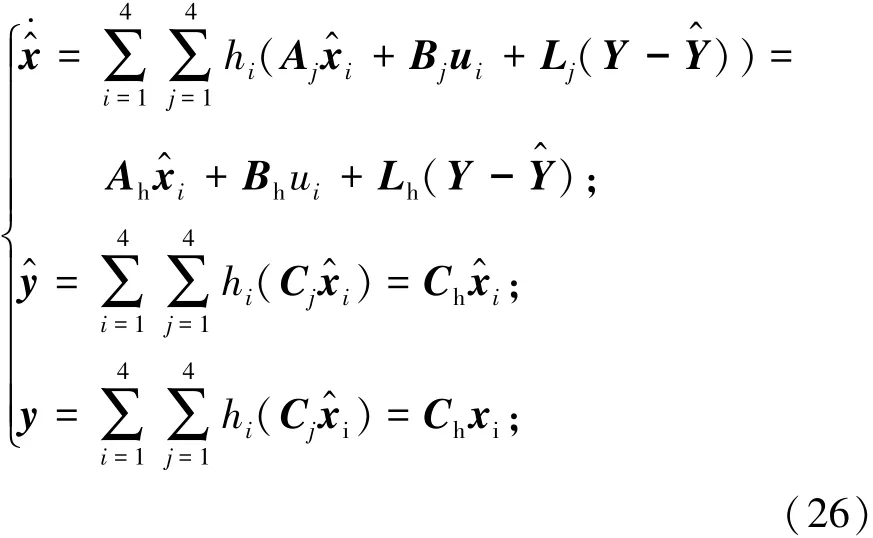
且

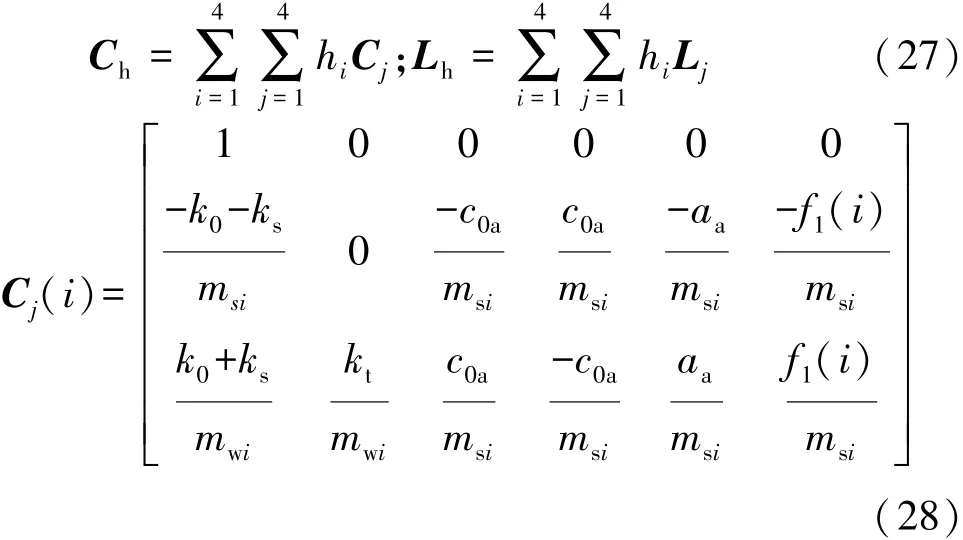
考虑到式(26)需用测量的信号来有效地对状态进行估计，因此设计了悬架运动误差模型：

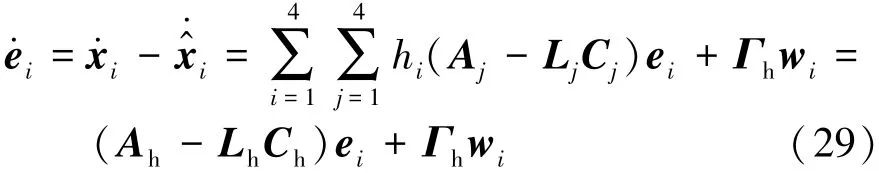
其中 ei＝xi-

设计T-S模糊观测器为了减小状态误差分布的影响，式(26)可表示为

很容易看出，如果存在一个矩阵P-＞0满足以下LMI不等式：

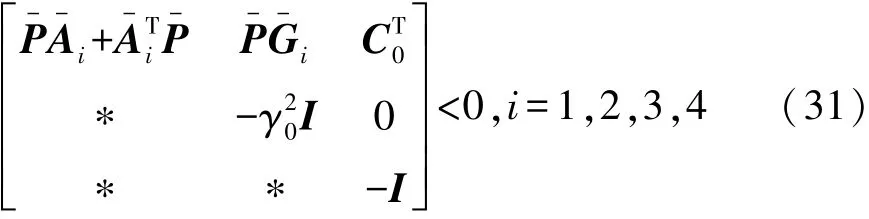
式(31)在H∞干扰衰减时趋于稳定，此时γ0＞0。定义Yi＝，并求解LMI不等式，观测器增益矩阵可表述为 Li＝。

3 T-S模糊观测器状态估计识别结果

基于上述理论分析，利用CarSim软件对T-S模糊整车观测器方法进行仿真验证，且转向盘转角输入如图4所示。

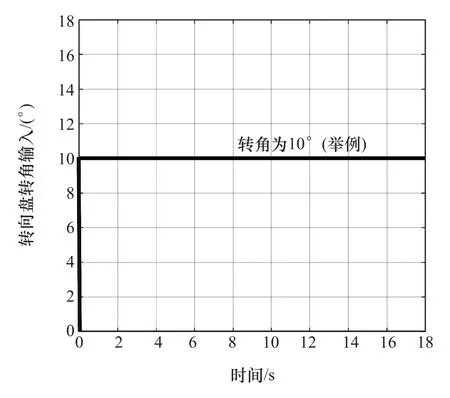
图4 路面激励工况下车辆侧倾转向盘转角输入

在CarSim中，以标准A/C级路面(80km/h)J-turn试验工况为例，进行了转向盘转角 10°车速80km/h的仿真实验。在标准A级和C级路面激励下将T-S模糊观测器估计值与CarSim仿真数据进行对比，车辆侧倾角和侧倾率的结果如图5和图6所示。

根据上述分析，计算出了在标准A级和C级路面激励下估计偏差的误差值，如表2所示。

由表2可见：最大SD误差值小于12%，因此采用该算法可获得车辆系统侧倾运动的较高状态估计精度。

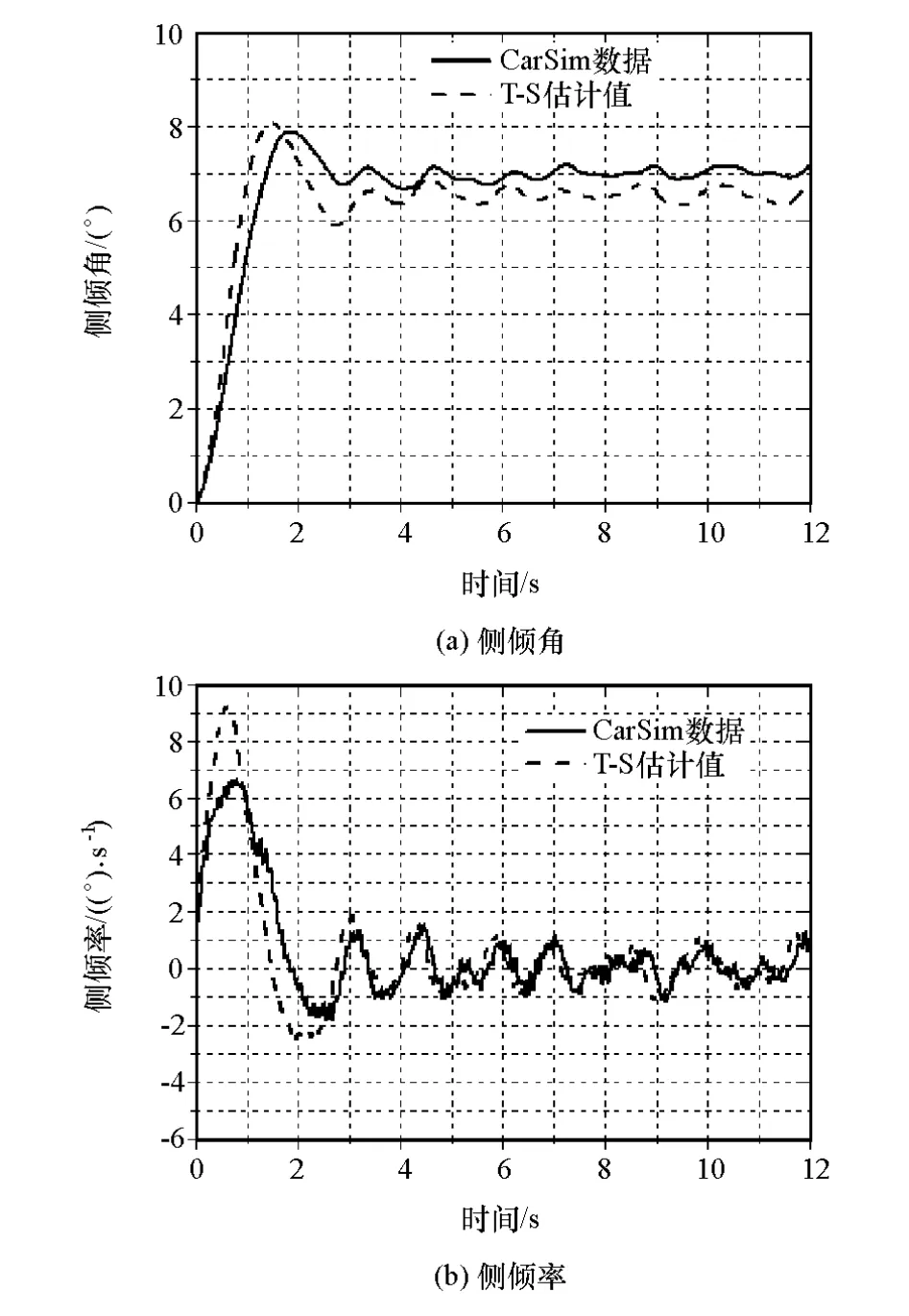
图5 标准A级路面激励下侧倾运动结果

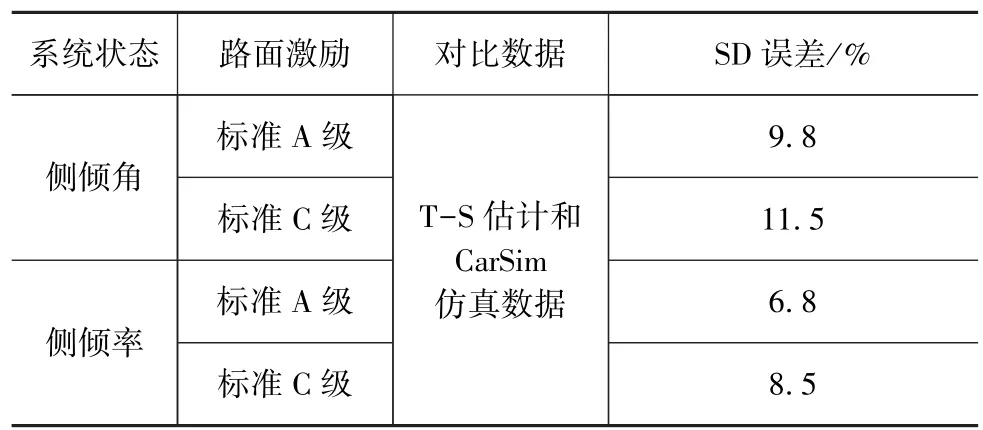
表2 在标准A/C级路面车速为80km/h时T-S模糊观测器估计误差值

4 结论

本文中搭建了基于车辆横向和垂向运动学的T-S模糊观测器，可用来对非线性整车系统的侧倾运动进行状态估计，利用该方法可获得较高的状态估计精度，从而更好地消除由车辆侧倾带来的危险。主要结论如下：

(1)基于车辆运动学耦合理论，首先建立了以路面轮廓作为未知系统的输入下整车横向和垂向耦合的9自由度运动学模型；

(2)在多种路面激励下，设计了整车T-S模糊模型和观测器来对整车侧倾行为进行状态估计，并且利用了LMI理论来阐述整车模糊观测器的稳定性，仿真结果显示，该方法可以获得较精确的数据；

(3)在CarSim运动学软件中对该T-S模糊观测器在相同条件下的状态估计进行了验证，仿真和验证的结果显示，对整车系统侧倾运动状态估计的最大SD误差值小于12%。

对于模型的精确度后续应增加实车实验对其进行验证，以说明此模型在车辆悬架系统侧倾运动状态估计中的准确性和实用性。