基于模型预测控制的混合动力汽车模式切换中的转矩协调控制策略∗

张渊博，王伟达，项昌乐，黄 琨，马 越，魏 超，李子龙

(北京理工大学机械与车辆学院，北京 100081)

前言

近年，在环境污染和石油资源短缺的实际背景下，新能源汽车得到了越来越多企业和科研机构的青睐。目前市场上新能源车辆主要有纯电动汽车、燃料电池汽车和混合动力汽车[1]。其中混合动力车辆可通过多种工作模式之间的协调切换，有效提高其燃油经济性。然而在模式切换过程中，由于系统的不连续性等特性，仍会出现平顺性差、冲击度大等问题。本文中基于双模混联式汽车对该问题进行了深入的研究。

1 技术研究现状

近年专家学者对混合动力汽车进行了大量的研究，内容包含了车身构型、能量管理和模式切换等多个方面，均取得了显著成果，其中关于模型切换过程的主要研究成果如下。

Beck R等人基于并联式混合动力汽车，利用模型预测控制算法通过对发动机和电机的转矩进行动态协调分配，提出了模式切换过程协调控制策略[2]；针对模式切换过程，Sul S K等人从优化换挡规律着手，提升了机械传动的效率，并通过电机调节离合器两端的转速差，减小了模式切换过程中车辆所受到的内部冲击[3]；Nelson D J等人设计了基于PID控制的模式切换过程控制策略，利用驱动电机调速实现离合器两端转速的同步，降低了模式切换时离合器接合过程中的冲击[4]。

针对模式切换过程的冲击问题，Gu Y等人首先通过最小值原理对动力系统的转矩进行了优化，然后基于模糊PID控制理论综合控制离合器接合过程的执行机构速度和节气门开度，同时利用电机转矩补偿需求转矩和离合器输出转矩中的差额，显著提升了模式切换过程中的平顺性[5]；针对模式切换过程中转矩波动大的问题，王庆年等人提出了利用电机补偿的模式切换控制策略[6]；山东大学的孙静提出了基于数据驱动预测控制的转矩协调控制方法，通过跟踪输出参考序列并限制离合器的转矩变化率，实现了模式切换时间短和冲击度小的目标[7]。

Rizzoni G等人针对并联式混合动力汽车，将其模式切换过程依据不同阶段特性划分成了多个子区域，并基于最优控制理论设计了不同子区域的子控制器，通过仿真验证了该策略的有效性[8]；同样，Soliman I S等人将双驱动混合动力汽车的模式切换过程划分为4个阶段，针对不同阶段设计了协调控制策略，并通过道路试验对所提出的控制策略进行了验证[9]；Kim H等人设计了并联式混合动力汽车模式切换过程4阶段控制策略，并在每阶段设计了相应的扰动观测器，通过对系统扰动的观测与补偿，提高了所提出策略的控制效果[10]。

赵治国等人针对模式切换过程中动力耦合所造成的汽车平顺性问题，提出了一种无扰动模式切换控制策略[11]；李亮等人针对并联式混合动力汽车模式切换中离合器接合过程，依据离合器的不同状态将其分为5个阶段，并对其中关键的滑摩阶段设计了基于H∞鲁棒控制和基于L2增益鲁棒控制的分层控制器，最后通过试验验证了所设计控制器的有效性和鲁棒性[12]。

综上所述，目前模式切换控制研究的对象多以并联式混合动力汽车为主，对双模混联式混合动力汽车模式切换过程研究较少，本文中针对双模混联式汽车，深入研究了其在不同机电混合驱动模式的模式切换过程，建立了功率耦合机构的等效模型，提出了基于模型预测控制的转矩协调控制策略。

2 等效模型

本文中所研究的机电复合传动(electro-mechanical transmission，EMT)系统如图1虚线框所示。该系统由发动机、电机、功率耦合机构等组成。

图1 机电复合传动结构简图

功率耦合机构如图2(a)所示，根据离合器C1和制动器BK的工作状态，功率耦合机构可以实现EVT1和EVT2两种机电混合驱动模式，EVT1模式下离合器C1断开，制动器BK接合，该模式适用于低车速状态下大转矩需求的工况；EVT2模式下离合器C1接合，制动器BK断开，该模式适用于高车速状态下小转矩需求的工况。

综合考虑发动机、电机和行星齿轮机构的转动惯量，建立从EVT1模式到EVT2模式的模式切换过程中的动力学模型：

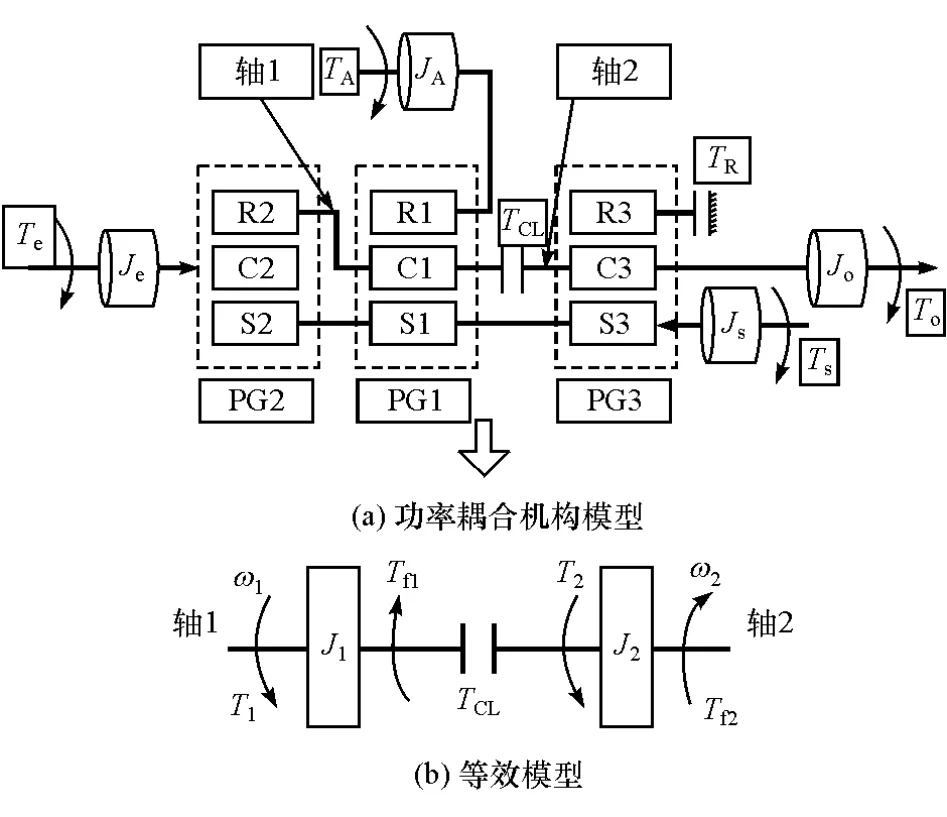
图2 机电复合传动拓扑结构

式中：JA为电机A转动惯量；JB为电机B转动惯量；Jo为输出轴的等效转动惯量；Jsi，Jri，Jci(i＝ 1，2，3)分别为太阳轮、齿圈和行星架的转动惯量；Tf为负载转矩；Tsi，Tri，Tci(i＝1，2，3)分别为太阳轮、齿圈和行星架的转矩；TCL，TBK分别为离合器C1和制动器BK的转矩；ωc1，ωr3分别为PG1行星架和PG3齿圈的角速度；ωA，ωB分别为电机A和电机B的角速度；ωi为功率耦合机构的输入角速度。

为方便研究离合器动态特性对机电复合传动EVT模式切换的影响，将功率耦合机构模型简化为围绕离合器主被动端的等效模型，如图2(b)所示。图中：J1，J2分别为轴1和轴2的等效转动惯量；ω1，ω2分别为轴1和轴2的角速度；T1，T2分别为轴1和轴2的等效转矩；Tf1，Tf2分别为轴1和轴2上由负载引起的阻力矩。

等效模型轴1的动力学方程：

等效模型轴2的动力学方程：

式中：行星架C1的角速度为轴1的角速度，即ω1＝ωc1；输出轴的角速度为轴2的角速度，即 ω2＝ωo。

发动机和电机的角加速度由下式确定：

式中：iq为前传动齿轮传动比；Jfq为行星排内部的转动惯量；Je为发动机的转动惯量。

各部件角速度之间的关系式为

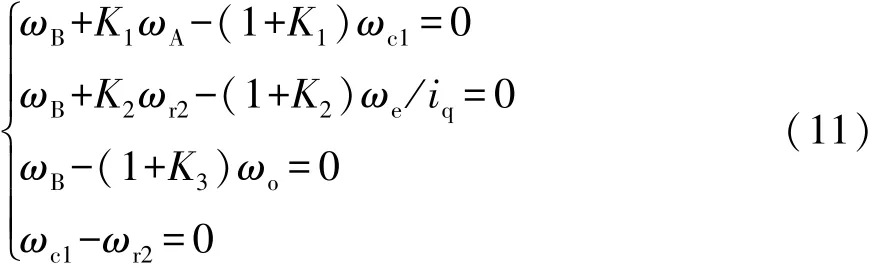
式中K1，K2和K3分别为PG1，PG2和PG3的特性参数，其为该行星齿轮齿圈的齿数和太阳轮的齿数之比。

各部件的转矩关系式为

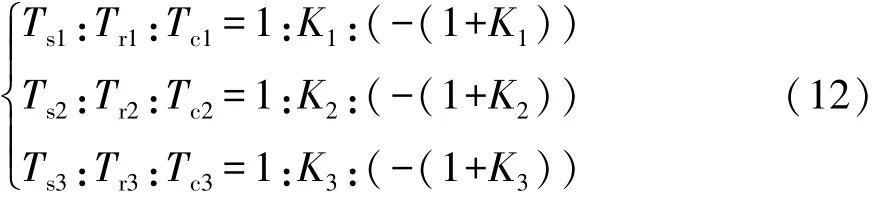
结合上述公式，可得轴1的转矩方程为

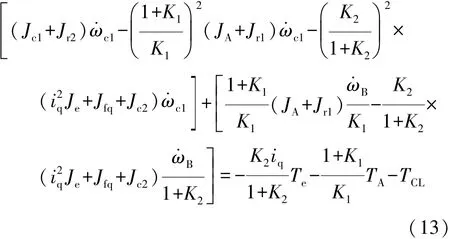
由于行星排内部的惯量较小，在此忽略不计，则有

由式(11)可得

由式(14)可得

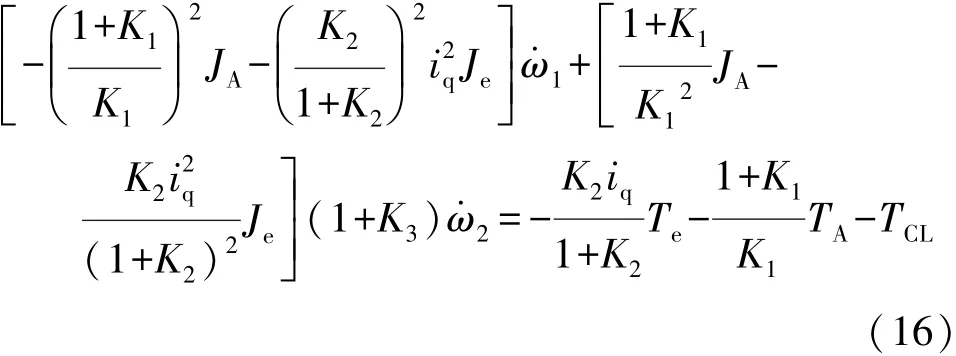
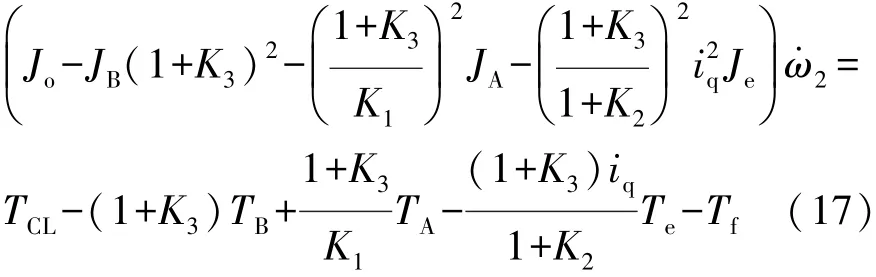
整理可得

其中

根据图2(b)，机电复合传动等效模型的动力学方程为

因此，图2(a)和图2(b)中转矩和惯量的等效关系为

3 基于模型预测控制的转矩协调控制策略

模型预测控制是一种在线滚动的优化算法，它在每一个控制步长，都会求解相应预测时域内最优控制问题，并将最优控制序列的首行元素作为控制变量输出，从而达到预估的控制效果，该方法可以预测被控系统的性能状态，适用于比较复杂且多目标的控制过程[13-14]。本文中针对离合器接合过程中的冲击和滑摩损失相矛盾的问题，基于模型预测控制方法设计了两者兼顾的转矩协调控制策略。

3.1 面向离合器接合过程的动态方程与问题描述

根据离合器的主从动盘转速和位置，离合器接合过程可划分为以下3个阶段。

(1)离合器分离阶段

该阶段主从动盘未接触，相互之间不传递转矩，此时运动方程为

(2)离合器滑摩阶段

当离合器主从动盘开始接触，但两者转速不一致时，离合器处于滑摩阶段，此时，随着执行机构的操作，离合器主从动盘之间压力逐渐增大，传递转矩也随之增大，该阶段运动方程为

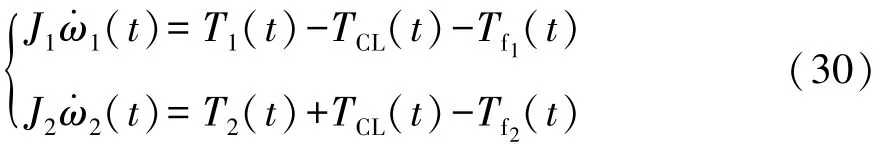
(3)离合器同步阶段

当离合器主从动盘接合且两者转速一致时，离合器处于同步阶段，该阶段运动方程为

式中ωm为离合器同步阶段主从动盘的角速度。此时离合器可看做刚性连接，则有

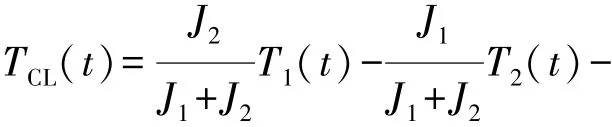
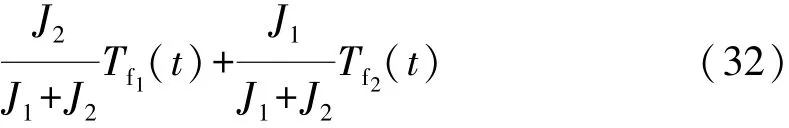
基于控制理论，下面对式(14)和式(15)中的变量进行相应的处理。状态量可定为x1(t)＝ω1(t)，x2(t)＝ω2(t)；输入量为 T1(t)＝u1(t)，T2(t)＝u2(t)，TCL(t)＝u3(t)；输出量为 y1(t)＝ x1(t)，y2(t)＝x2(t)；扰动量为 d1(t)＝ Tf1(t)，d2(t)＝ Tf2(t)。

3.2 过驱动系统控制分配

经过处理后，在滑摩阶段的状态空间方程为

其中：x＝[x1(t)x2(t)]T；u＝[u1(t)u2(t)u3(t)]T

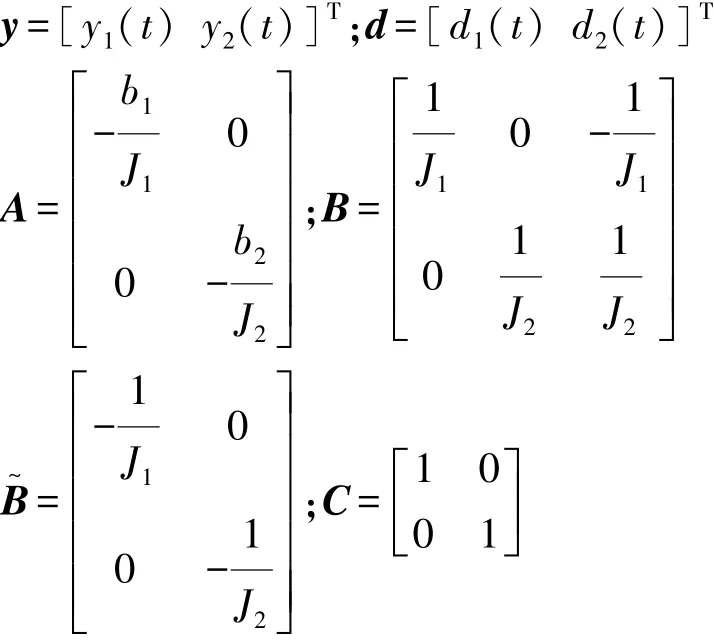
由于3个输入转矩皆存在上下限，应对其进行约束，其方程为

该系统控制输入量u的维数大于输出量y的维数，因此是一个过驱动控制系统[15]。为解决该问题，引入虚拟控制量v＝[v1v2]T，v1和v2分别为轴1和轴2上的转矩，虚拟控制量为

因此控制矩阵B可分解为

则式(18)可简化为

其中vmin＝[u1min-u3minu2min+u3min]T

vmax＝[u1max-u3maxu2max+u3max]T

该控制系统的整体架构如图3所示，首先上层策略依据驾驶员操作和车身状态发出模式切换指令，然后参考模型基于参考控制量计算出相应的参考转速，模型预测控制器基于参考转速和车身反馈的实际转速，结合增广模型及目标函数，求解出最优虚拟控制量，继而利用最优分配策略对该虚拟控制量进行分配，最后得到实际的最优控制量，它与扰动共同作用于整车，在保证整车车速跟踪性与平顺性的同时快速完成模式切换过程。

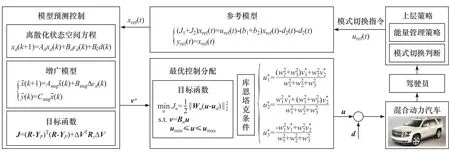
图3 基于MPCA的转矩协调控制框图

3.3 参考模型

选取离合器接合后的状态作为参考模型，离合器接合后轴1和轴2的转速相同，系统由等效转矩T1和T2共同驱动，使被控对象的实际输出量即转速跟踪参考模型的状态量。参考模型的动力学方程为

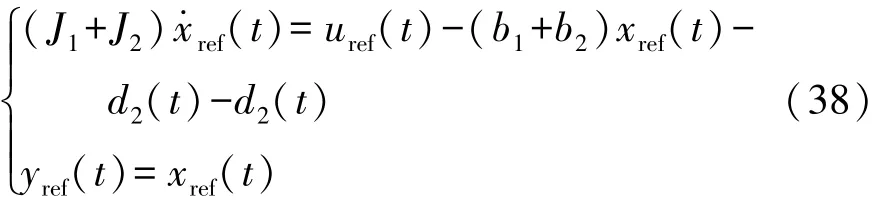
式中：xref(t)为参考转速；uref(t)为参考转矩，且uref(t)＝ u1(t)+u2(t)。

3.4 模型预测控制器设计

为了实时在线计算，将等效模型离散化，设定采样时间为τs，则离合器在滑摩阶段的表达式为

为减少或消除静态误差，将式(39)运用差分运算并改写成增量模型：

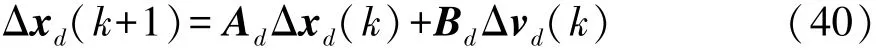
其中状态增量为

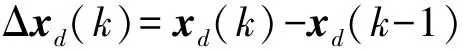
控制增量为

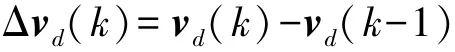
定义新的状态变量：

则新的增广模型为

其中

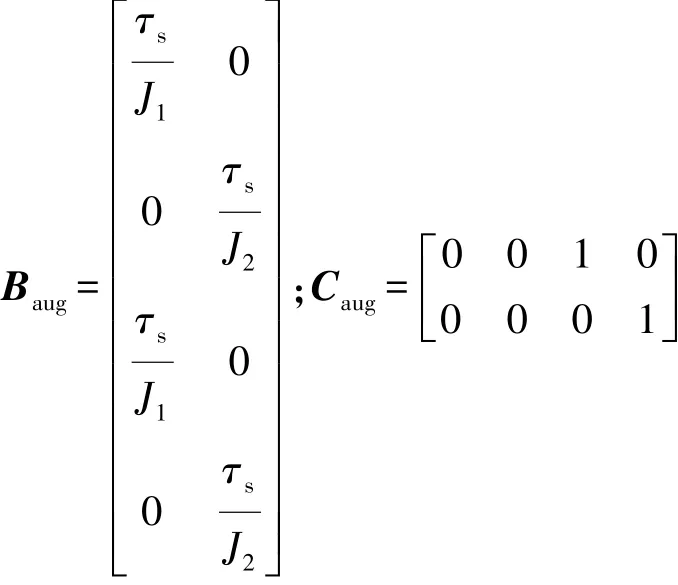
模型预测控制中，每一个采样时间内的算法运算量主要受预测时域N、控制时域M和系统模型的复杂程度3个因素的影响，本文中设定预测时域为6，控制时域为4，因此 v-(k)＝ v-(k+1)＝ …＝v-(k+5)。

则式(42)增广模型可表达为

在滑摩阶段，设定r(k)＝[yref(k) yref(k)]T作为输出量y1(k)和y2(k)的参考信号，使离合器两端轴1和轴2的转速能实时跟踪信号r(k)。因此，设定目标为使离合器两端转速和参考转速之间误差最小，目标函数表达式为

式中：R为参考信号的矢量矩阵；Rv为调节控制矢量的权重矩阵。

使目标函数最小的必要条件为

求解得到的最优控制增量ΔV为

则系统当前时刻最优虚拟控制量为

3.5 最优控制分配

根据上述公式可求得的使离合器两端转速与参考信号误差最小的虚拟控制量v∗，该虚拟控制量仍需分配到实际控制量u即发动机和两个电机的输出转矩上。为了保证离合器传递转矩时的连续性，采用以控制量最小化为目标的分配方法进行优化[16-17]，优化模型为

标控制量。该优化问题的拉格朗日函数为

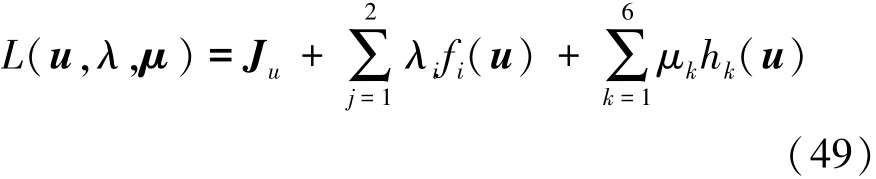
其中

式中：fi(u)(i＝1，2)为等式约束；hk(u)(k＝1，2，…，6)为不等式约束。

采用库恩塔克(Karush-Kuhn-Tucker，KKT)条件[18]求解此类同时存在等式和不等式约束的最优化问题：

最终求得实际最优控制量为

4 仿真与结果分析

为验证模式切换过程中基于模型预测控制的转矩协调控制策略(model predictive control allocation，MPCA)的有效性，采用现阶段广泛应用的基于规则的控制方法作为基准(Baseline)，用以对所提出的控制策略进行对比，由于基准控制策略不是本文研究重点，此处不再多加描述，详细内容可见文献[1]。仿真中设定离合器接合两端转速差的阈值为200r/min，控制器采样时间为0.01s，虚拟控制量的权重矩阵为Rv＝diag(4，2)，实际控制量的加权矩阵为Wu＝diag(2，1，3)。

模型预测控制策略与作为基准的规则式控制策略的仿真结果如图4所示。从图4(a)和图4(b)可以看出，模型预测控制策略通过协调控制等效转矩T1(t)和T2(t)，有效地补偿了离合器接合过程中的摩擦转矩；由图4(c)和图4(d)可知，模型预测控制的离合器滑摩时间为0.42s，而规则式控制策略的滑摩时间为0.58s，减少了27.59%；如图4(e)所示，在模型预测控制策略中车速的变化更为平缓，说明该策略下驾驶平顺性更好；由图4(f)、图4(g)和图4(h)可知，模型预测控制策略的加速度波动范围为0.142～0.215m/s2，最大冲击度为 0.15m/s3，离合器接合过程的滑摩功为1 944J，而规则式控制策略的加速度波动范围为-0.03～0.22m/s2，最大冲击度为14.61m/s3，且滑摩功为4 280J。表1详细给出了离合器接合过程中MPCA与Baseline方法的仿真结果对比。

图4 MPCA和Baseline仿真结果对比

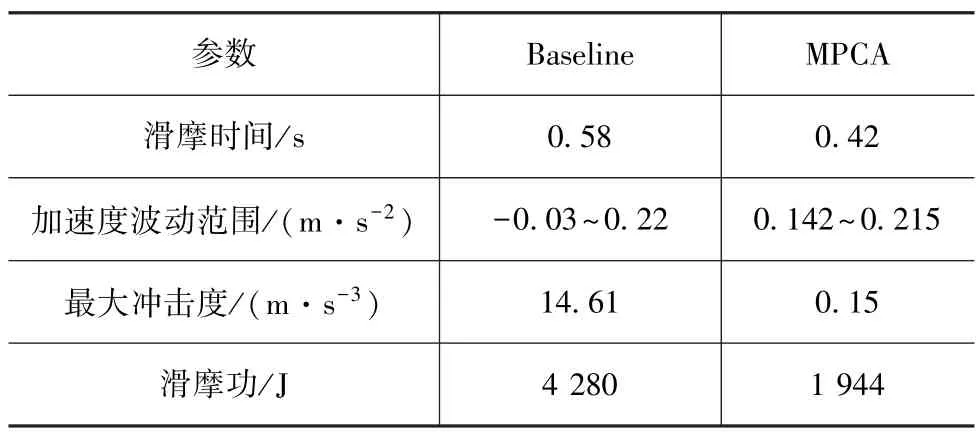
表1 MPCA与Baseline仿真结果对比

因此，本文中所提出的基于模型预测控制的模式切换过程转矩协调控制策略能在保证车速稳步上升的同时，使加速度的波动范围更小，冲击度大幅度降低，且离合器的滑摩损失只有基准的45.42%。

5 结论

本文中以双模混联式机电复合传动为研究对象，以改善模式切换品质为研究目的，重点围绕离合器接合过程控制策略展开研究。首先，对本文中所研究的机电复合传动总体结构和特性进行了分析，并采用理论与试验相结合的方法建立了功率耦合系统的等效模型；其次，提出了以减小车辆冲击度和离合器滑摩功为目标的基于模型预测的转矩协调控制策略；最后，利用仿真模型，对转矩协调控制策略进行了验证。结果表明，机电复合传动在所提出的模式切换控制策略的作用下，能在保证模式切换响应速度更快的同时，有效降低输出轴的转矩波动，并在大幅度降低车辆冲击度的同时，减小约一半的离合器滑摩损失，因此极大地改善了模式切换品质，对于工程实践具有一定的参考价值。