基于环境态势评估的智能车自主变道决策机制∗

何艳侠，尹慧琳，夏鹏飞

(同济大学中德学院电子信息系，上海 200092)

前言

据统计由于变道造成的交通事故占有很大的比例，如果驾驶员在变道时不注意观察周围的环境，或者判断失误，或没有注意到前方车辆变道，都极易造成交通事故。自主变道与辅助变道系统可有效预防交通事故的发生。变道时驾驶员的视觉特性和车辆的运动情况等参数被深入分析[1-3]，为变道意图识别提供更多的数据支撑。Kumar P等人使用贝叶斯方法分析驾驶员数据来预测车辆变道意图[4]。在车辆变道轨迹规划方面，提出了一种新的车辆变道函数，并引入B样条理论对该函数进行再规划从而建立一种新的车辆变道模型[5]。在车辆变道决策方面，用模糊逻辑描述车辆变道规则[6]。还有用机器学习的方法学习驾驶员经验，提出了基于驾驶员经验的自动驾驶车辆变道决策模型[7]。Ulbrich[8]和Brechtel[9]等人使用马尔可夫模型进行变道决策研究。Chen[10]和Habenicht[11]等人利用质点运动方程来计算为避免碰撞汽车所需的加速度，从而判断变道是否可行。Ulbrich[12]等人针对变道行为决策，综合考虑道路场景、周边车辆状态和车辆自身状态参数，进行态势估计，得到向左、向右变道的可能性概率和获益概率。自主变道决策的研究虽然取得了一定进展，但在正确合理性方面尚待进一步完善，谷歌智能车于2016年发生首次担责事故，事故原因是智能车变道时对周围目标行为预测判断失误，导致与侧后方公交车发生蹭撞。

由于在保障安全、提高效率、改善环境和节约能源方面的优势，智能车已成为国内外广泛关注的焦点。智能车是集环境感知、路径规划决策和控制等功能于一体的综合智能系统，环境感知为规划决策提供信息支持。汽车面对的行驶环境是高动态复杂环境，且由于车载传感器和处理器等限制，其信息存在高度不确定性，所以对动态环境进行正确态势评估是提高车辆行驶安全性的关键因素之一[13]。而智能车，不依赖于人类驾驶员，完全根据对周围交通环境态势的评估做出正确的决策，来自主地操纵车辆，因此，智能车对环境态势评估的要求更高。人类驾驶已经积累大量经验和知识，态势评估[13]对数据流的高层次关系进行提取与处理，接近人的思维推理过程，涉及到众多因素和抽象信息，很大程度上依赖领域知识，由此借助人类认知机理对智能车环境态势评估进行分析。智能车环境态势评估在感知目标状态的基础上，分析正在发生的事件，预测未来发生的事件，由于目标状态具有不确定性，所以借助贝叶斯网络[14]实现不确定性推理和决策。

本文中基于智能车环境态势评估，研究自主变道决策。首先基于人类驾驶认知机理，将智能车环境态势评估分为目标感知、情境理解和态势预测3个层次，然后利用动态贝叶斯网络实现情境理解和态势预测，并结合期望效用最大化原则实现自主变道决策，最后通过实验验证了本文方法的有效性。

1 智能车环境态势评估和动态贝叶斯网络

1.1 智能车环境态势评估

态势评估在军事和网络安全领域已得到广泛研究和应用，根据信息的抽象层次，分为态势感知、态势理解和态势预测3个层次[15]。基于人类驾驶认知机理的分层记忆机理，按照被处理信息由低到高的抽象层次，本文中将态势评估分为目标感知、情境理解和态势预测3个层次，目标感知是指对单个目标的检测和识别，即对GPS/惯导、图像、毫米波雷达和激光雷达等传感器数据进行处理，提取基本特征参数，如障碍物目标的大小和路沿点位置等；情境理解是对目标、事件或场景的理解，即对基本特征参数进行分析，提取抽象特征参数，如归一化相对位置、安全减速度和碰撞时间等，进而判断车道占用和碰撞等风险发生的可能性；态势预测则是对将要发生的事件及态势进行预测，为规划决策提供信息。

贝叶斯网络作为一种知识表示和进行概率推理的框架，在具有内在不确定性的推理和决策问题中具有显著优势[16]。

1.2 动态贝叶斯网络的表示与推理

贝叶斯网络用一组条件概率函数和有向无环图对不确定性的因果推理关系进行建模，主要用于概率推理与决策[16]。动态贝叶斯网络是在静态贝叶斯网络上加上时间因素，克服了系统在时间依赖表达和计算上的困难，具有强大的动态不确定性问题处理能力[17]。贝叶斯网络由代表变量的网络节点X＝{X1，X2，…，Xn}、连接这些节点的有向弧和条件概率表(conditional probability table，CPT)组成。节点代表随机变量，节点的有向弧代表了节点间的互相关系(由父节点指向子节点)，用条件概率表表明了子节点与父节点之间概率依赖的数量关系，其中父节点用pa(Xi)表示。没有父节点的用先验概率进行信息表达。由概率链规则可得

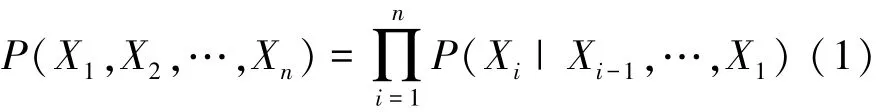
假设每个变量都条件独立于它的非子节点，则上式变为

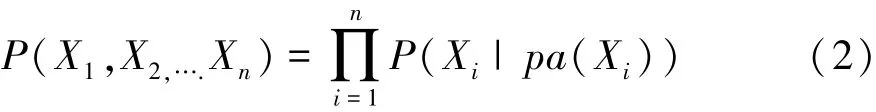
则

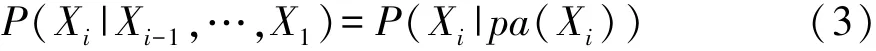
动态贝叶斯网络是贝叶斯网络在时序空间中的延伸，其推理的本质与贝叶斯网络一致。贝叶斯网络推理实际上就是在给定某些节点的概率取值之后，计算其关联节点的概率分布，进而计算某一事件

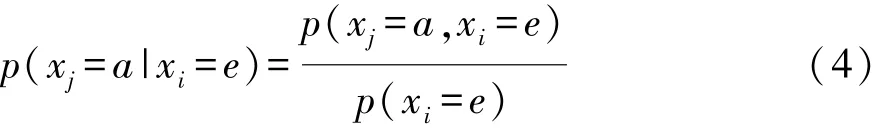
1.3 期望效用最大化原则

期望效用最大化是不确定性决策的基础。态势预测为智能车的规划决策提供信息，决策即从几种可能的结果或采取的行动 C＝{C1，…，Ci，…，Cn}中选择最有利的或最喜欢的。但在结果或行动不完全确定的情况下，决策制定变得非常困难。为此，本文中为每种可能的结果或行动指定了数值化的效用U＝{U1，…，Ui，…，Un}，表达对结果或行动的偏好。每种结果或行动的期望效用EUi，即结果或行动的概率值和效用U的乘积，即

然后比较每种结果或行动的期望效用，具有最大期望效用的结果或行动即是最佳的结果或要采取的行动。这样既考虑了结果或行动的不确定性，又顾及了决策者对结果或要采取行动的偏好。发生的概率。

贝叶斯网络的主要推理[18]模式有两种：(1)自上而下的因果推理，就是给出父节点的参数分布来计算子节点的概率，即由已经掌握的原因(证据)推出在该原因下结果发生的概率；(2)自下而上的诊断推理，是已知后代节点参数分布，推算父节点的概率和参数分布，即由结果逆向探索导致该结果事件发生的原因和概率。

由此，推理过程可简单描述为：在已知某些节点的概率xi或者已知证据(记做e)时，求未知节点xj取某一特定值a的概率，即计算条件概率：

2 基于动态贝叶斯网络的态势评估实现及变道决策

2.1 动态贝叶斯网络构建与推理

由于贝叶斯网络在处理不确定性推理和决策问题中的优势，本文中基于贝叶斯网络实现情境理解和态势预测。结合这3个层次，构建的自主变道贝叶斯网络如图1所示。

图1中情境理解层对应于贝叶斯网络的7个节点，分别为：归一化横向位置(normalized lateral position， NLP)，安全减速度(deceleration to safety time，DST)，左右两个车道线的实虚类型，本车道和左右两车道的状态。态势预测层对应于贝叶斯网络的3个节点，分别为：保持本车道行驶、左变道和右变道。依据相应3个事件的安全效用值，为规划决策提供支持。

图1 车辆换道贝叶斯网络

为了简化计算，本文中假设场景是车在3条直线车道上行驶，如图2所示。设每条车道的宽均为w，建立以P为中心的坐标系，其中x轴平行于车道边界线，y轴垂直于车道边界线，则MN＝w，令MP＝o，且 o＝w/2。

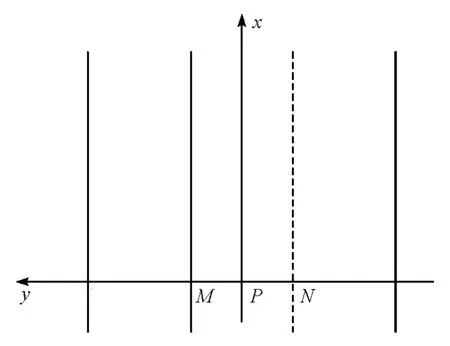
图2 车道模型

归一化横向位置NLP表示每辆车j的侧向位置lj，即确定每辆车在哪条车道上：

式中y为车的y轴方向的坐标值。

由于车载传感器数据具有不确定性，NLP只能被估计，由贝叶斯公式可得车的侧向位置，即NLP的概率公式为

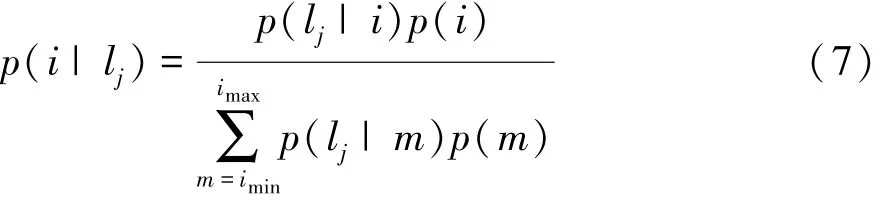
式中：i和m表示车道；p(i)为车位于i车道的概率；p(i｜lj)为给定NLP的情况下车位于i车道的概率。

由于车道满足均匀分布，即p(i)＝p(m)，则

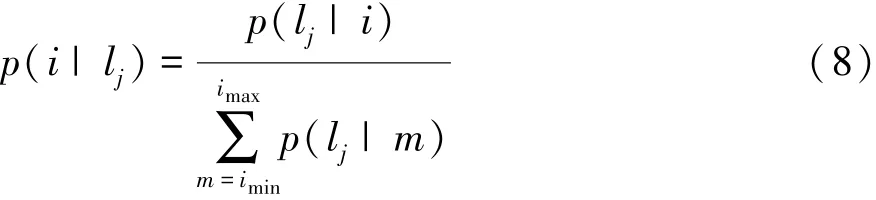
而

式中σj，l表示第j辆车NLP的方差。

安全减速度DST表示车j减速到和前面障碍物保持安全距离所需的最大加速度dj：

式中：ve为本车的速度；vo为障碍物的速度；ts为安全时间；x为安全距离。

dj在不同的状况下具有不同的值，可分为3种情况：危险(D)、占据(O)和自由(F)。危险指的是本车道或者要换的车道上有车且和本车距离比较近，很容易发生碰撞；占据指本车道或者要换的车道上虽然有车，但是和本车距离相对较远；自由指的是本车道或者要换的车道上前方无车或者和本车距离特别远。且由于传感器的不确定性，dj也具有不确定性，在不同的状况下的概率如下：

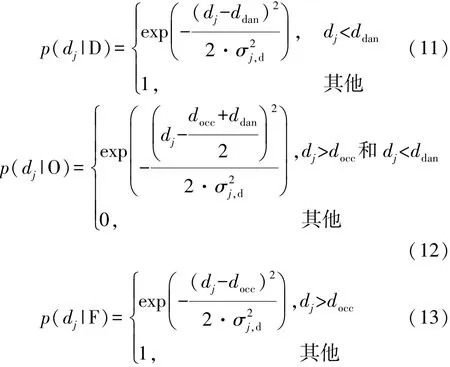
式中：ddan和docc分别为危险和占据情况时的临界加速度；σj，d为第 j辆车的 dj的方差。 由式(11)～ 式(13)和贝叶斯公式可得车道状态的概率：

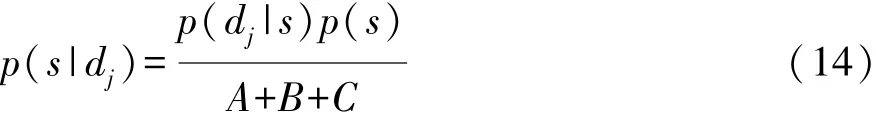
其中 A＝p(dj｜D)p(D)

式中s为车道状态。

由于道路状态满足均匀分布，即p(D)＝p(O)＝p(F)，则式(14)可以简化为

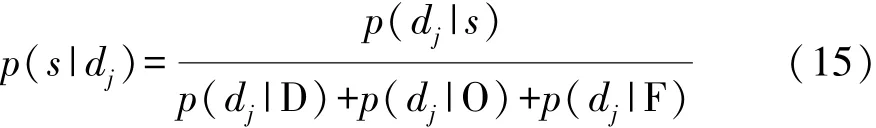
由式(9)和式(14)可得每条车道各个状态的概率：

式中：j为障碍物车的数目；q为障碍物车所在的车道。

根据专家知识，向左变道的条件概率表(CPT)如表1所示。

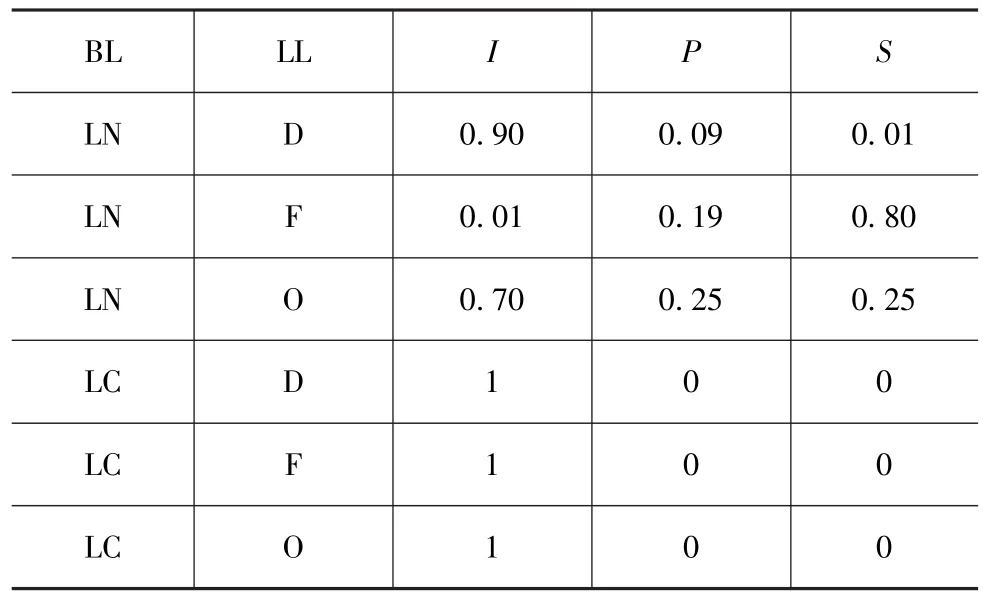
表1 向左变道的条件概率表

向右变道的条件概率表(CPT)如表2所示。

本文中将汽车的速度和位置设定为随时间变化的量，因此在贝叶斯网络的基础上加上随时间变化的汽车速度和位置，即建立了动态的贝叶斯网络。

2.2 变道决策

变道决策即在保持本车道、向左变道和向右变道3种可能性中选择最佳的。根据最大期望效用原可能和安全的效用。

表2 向右变道的条件概率表

最后比较EKL，ECL和ECR3个值的大小，最大的即代表最佳选择。比如若EKL最大，则本车此时应继续保持本车道前行。

3 实验与结果分析

则，即比较3种行为的安全效用，最大的即是最佳选择。保持本车道的安全效用值：

式中：PD，PO和PF分别为本车道危险、占据和自由的概率；UD，UO和UF分别为危险、占据和自由3种状态的效用值。类似地，向左变道的安全效用值：

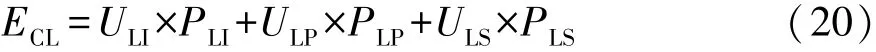
式中：PLI，PLP和PLS分别为向左变道不可能、可能和安全的概率；ULI，ULP和ULS分别为向左变道不可能、可能和安全的效用。

向右变道的安全效用值：

式中：PRI，PRP和PRS分别为向右变道不可能、可能和安全的概率URI，URP和URS分别为向右变道不可能、

为验证用贝叶斯网络和期望效用最大化决策车变道的正确性，对以下3种典型场景进行分析。

场景1：本车在中间车道，规定 ve＝90km/h，本车正前方有一辆障碍物车，vo＝70km/h，两辆车间距为1km，左边车道线是实线，右边车道线是虚线。效用值分别为：EKL＝0.1693，ECL＝0.0831，ECR＝0.7476。ECR最大，即本车应该向右变道，结果正确合理。

场景2：本车在中间车道，规定 ve＝90km/h，本车正前方有一辆障碍物车，vo1＝100km/h，两辆车间距为1km，本车的右车道有一辆车，且速度 vo2＝60km/h，它和本车之间的间距为800m，左边车道线是实线，右边车道线是虚线。效用值分别为：EKL＝0.5599，ECL＝ 0.2248，ECR＝ 0.2153。 EKL最大，即本车应该保持本车道前行，结果正确合理。

场景3：为动态场景，相应Prescan场景如图3和图4所示。

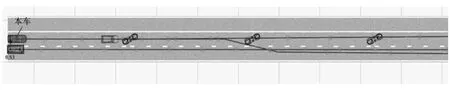
图3 场景3中开始时车的状态

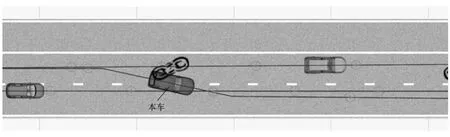
图4 场景3中变道时车的状态

本车在中间车道，在它的正前方和右边车道上均有一辆障碍物车。3辆车的起始速度均为15m/s，本车的加速度为4.11m/s2，正前方的车的加速度为2m/s2，右边车的加速度为0.47m/s2。本车在t≈2s时向右变道，在t≈3.5s时变道完成，本车沿着右边的车道继续行驶。3个期望效用值曲线如图5所示。

开始时EKL最大，即本车保持本车道运行，t≈2s时，ECR最大，即本车开始向右变道，从t≈3.5s后，EKL最大，即本车沿着右车道继续行驶，结果正确合理。

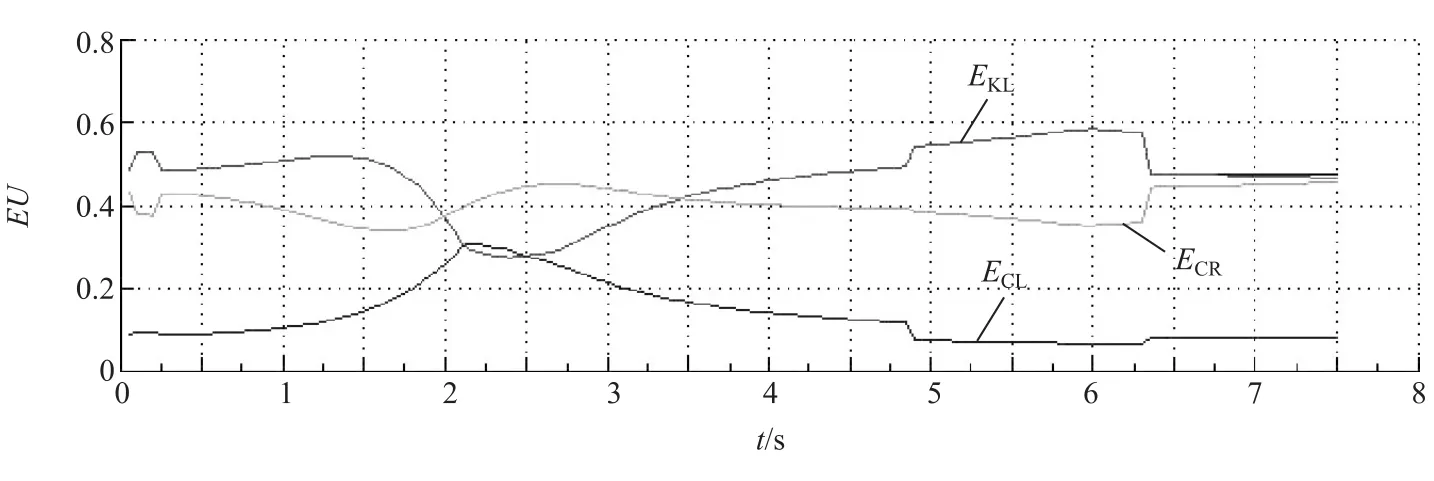
图5 保持本车道、向左变道和向右变道随时间变化的期望效用曲线

4 结论

针对智能车传感器信息的不确定性，本文中在态势评估的基础上研究自主变道决策机制。基于人类驾驶认知机理将智能车环境态势评估分为目标感知、情境理解和态势预测3个层次，然后利用动态贝叶斯网络实现情境理解和态势预测，最后结合期望效用最大化原则实现自主变道决策。典型场景实验的结果表明决策正确合理。本文中实验只选用了若干典型场景，测试场景还有待于复杂化和多样化，比如直车道换成弯道，增加周围障碍物目标车辆的数量和状态，以及变道模型设计为正弦函数变道轨迹等，这些都有待今后进一步研究。