基于DL-MOPSO算法的等效燃油消耗最小能量管理策略优化研究∗
石 琴,仇多洋,吴 冰,刘炳姣,陈一锴
(合肥工业大学汽车与交通工程学院,合肥 230009)
前言
混合动力汽车的能量管理是一个非线性、多变量、多目标的时变系统,其策略的优劣直接影响着混合动力汽车的动力性、经济性和排放性能。大量的文献从不同的角度提出了不同的能量管理策略。其中基于规则的管理策略主要是依据工程经验或实验数据反复调试控制阈值,因此较易实现,鲁棒性好,开发成本低,但依赖于经验水平,且工况适应性差[1-4]。基于全局优化的能量管理策略需要预知行驶工况信息,因此具有一定的局限性,难以用于实车控制[5-7]。而等效燃油消耗最小策略(equivalent fuel consumption minimization strategy, ECMS)具有结构简单,运算量小,无需先验知识,并且通过引入惩罚函数,使得该策略具有良好的电量保持特性,使其较好地适用于插电式混合动力汽车的电量保持阶段的能量管理,因此被广泛研究[8-10]。ECMS最早作为一个求解最小值方法由Paganelli提出,并应用在混合动力系统能量管理中[11];Aiyun Gao等人将ECMS应用在并联混合动力汽车的实时优化控制中,获得了较好的燃油经济性和电量保持性能[8];Chao Sun等人建立了一种带有车速预测的自适应ECMS,最终油耗减少超过3%[9];沈登峰等人基于庞氏最小值原理,建立以等效瞬时燃油消耗最小为目标的ECMS,结果显示油耗降低12.31%[12];詹森等人将行驶工况识别技术和ECMS结合起来,通过识别当前工况类型,调整等效因子,获得实时最优控制,与未采用识别相比,油耗降低7.47%[13]。苗强等人建立一种可变SOC参照的ECMS,相比于固定SOC参照,减少了23kJ等效能量消耗[14];徐成善等人在循环工况已知的前提下,将ECMS应用于某增程式混合动力汽车,结果表明ECMS更适用于增程式混合动力汽车[15];陈龙等人将ECMS应用于插电式串联混合动力城市公交车,硬件在环实验表明ECMS能减少能量的消耗,实时控制性好[16];林歆悠等人对ECMS中SOC惩罚系数进行修正,并利用遗传算法优化了修正系数,燃油经济性提高20.81%[17];司远等人将ECMS应用在四驱混合动力系统中,利用遗传算法优化充放电等效因子,硬件在环仿真表明,相比未优化的ECMS,燃油经济性提高2.68%[18]。
ECMS核心算法包括3个关键部分,第1部分是对于某一特定行驶工况,寻找最优充电和放电等效因子,第2部分是在确定等效因子的前提下,对于任意瞬时功率或转矩需求,求解发动机和电机的最优功率或转矩分配,第3部分是选择合理的惩罚系数,提高混合动力汽车的电量保持性能。而当前对于ECMS的研究大都侧重于某一部分,并未综合考虑3个部分对ECMS的影响,且研究过程中,大多采用离散穷举法获得最优充电和放电等效因子以及发动机和电机的功率分配方式,寻优结果较好,但未利用智能优化算法进行寻优。部分文献利用遗传算法获得最优充电和放电等效因子,而功率分配方式则采用穷举法获得,因此若在优化等效因子的同时利用智能算法对功率分配进行寻优,则可进一步提升整车燃油经济性。因此对于ECMS的优化问题,是一个不连续、非可导的内外层嵌套多目标优化问题,目前尚未见利用多目标智能优化算法同时对充放电等效因子和功率分配方式进行寻优的研究。
针对以上问题,本文中以降低燃油消耗量和减小SOC终值与目标值偏差为优化目标,建立基于P2构型的某ISG型混合动力汽车Simulink模型,利用模型描述ECMS参数与目标参数之间的非线性关系,提出一种内外层嵌套的双层多目标粒子群算法(double-loop multi-objective particle swarm optimization,DL-MOPSO)对充放电等效因子和功率分配方式同时进行寻优,即以目标函数最小的前提下,寻得最优充放电等效因子下任意需求功率时发动机和电机最优功率分配方式的Pareto解集前沿,对寻优结果进行仿真,与传统基于穷举法构建的ECMS相比,燃油经济性明显提高。
1 ISG型混合动力汽车结构与建模
本文中研究的ISG型混合动力汽车整车结构如图1所示。模型涉及的主要零部件包括发动机,电磁离合器C,ISG电机,蓄电池组,AMT自动变速器,主减速器,电子附件和车轮。动力及传动系统参数如表1所示。
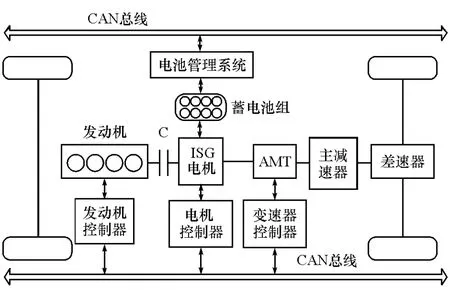
图1 整车动力传动系统结构图
1.1 整车纵向动力学模型
发动机和电机同轴相连,离合器闭合状态下转速相同,因此可根据转矩传递路径建模。具体运动学方程为
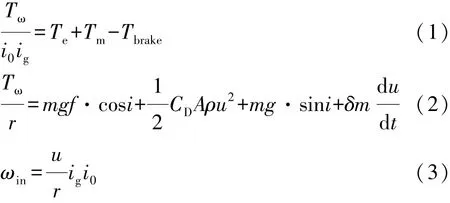
式中:Tω为车辆行驶所需转矩;Te为发动机输出转矩;Tm为电机输出转矩;Tbrake为摩擦制动转矩;i0为主减速器传动比;ig为变速器传动比;r为车轮半径;m为汽车质量;g为重力加速度;f为滚动阻力系数;CD为空气阻力系数;A为迎风面积;ρ为空气密度;i为道路坡度;u为车速;δ为汽车旋转质量换算系数;ωin为变速器输入轴旋转角速度;t为时间。
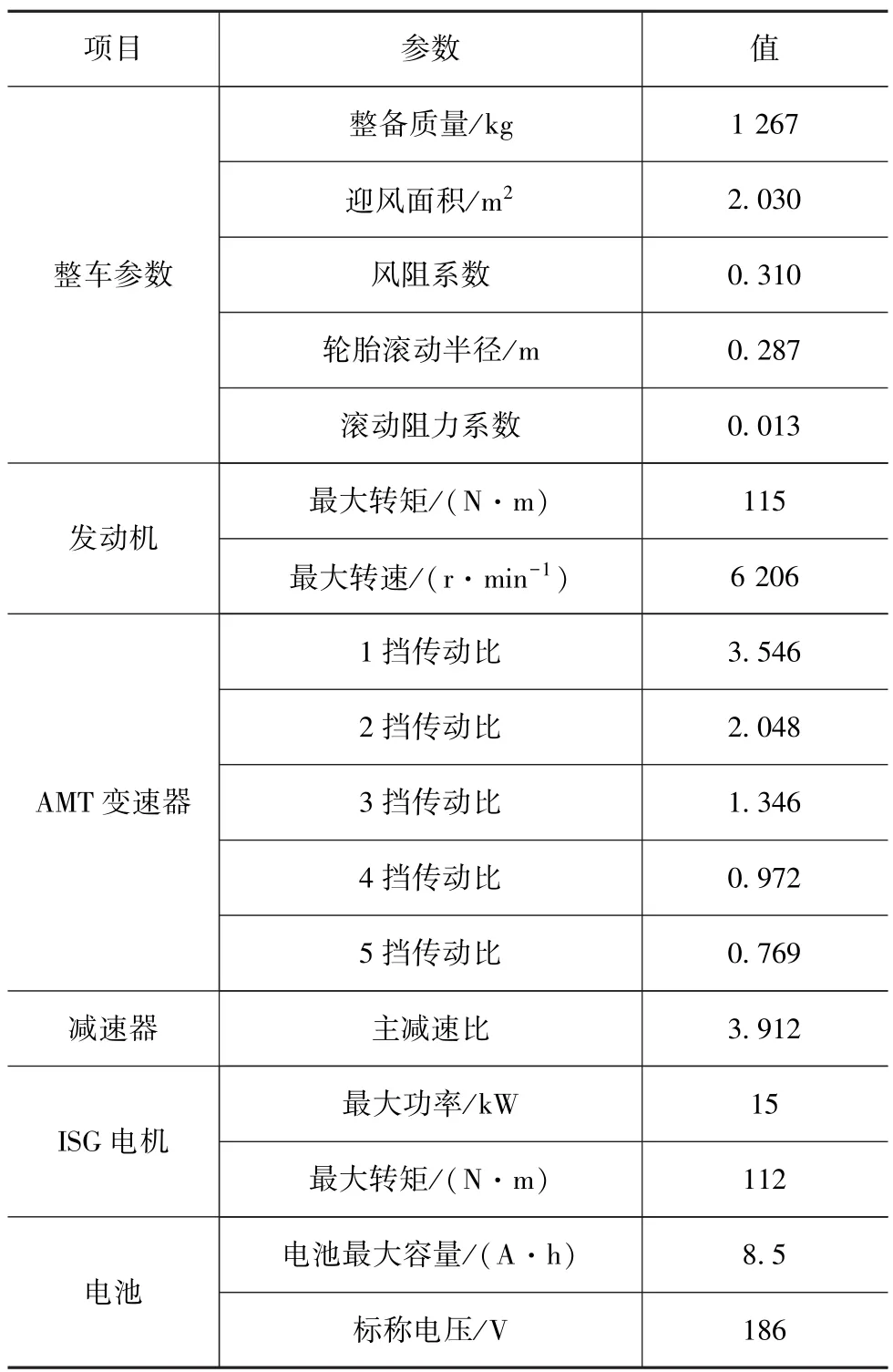
表1 动力及传动系统参数
1.2 发动机模型
发动机模型共包括两个子模块,分别是转矩计算模块和燃油消耗计算模块。采用实验数据法建模,即通过查询发动机速度特性曲线和万有特性曲线插值计算发动机实际输出转矩和消耗的燃油。方程如下:

式中:ne为发动机转速;α为节气门开度;Te为发动机输出转矩;bfuel为发动机瞬时燃油消耗率。
1.3 ISG电机模型
电机模型共包括3个子模块,分别是转矩计算模块、驱动模式电流计算模块和发电模式电流计算模块。转矩计算模块方程为

式中:Tm为电机输出转矩;nm为电机转速;U为电机工作电压。
在电流计算模块中,电机工作效率受电机工作状态影响较大,因此同样采用实验数据法建立电机效率模型,驱动和发电两种工作模式下电流计算方程为

式中:η为电机效率;Idis为驱动模式工作电流;Ichg为发电模式工作电流;Treg为制动回收转矩。
1.4 电池模型
电池模型采用内阻 开路模型,包括电池温度计算模块、电池开路电压及内阻计算模块、SOC估计模块,电压动态关系为

式中:Rbat为电池内阻;T为电池温度;SOC为电池荷电状态;Uocv为电池开路电压;SOC0为电池初始荷电状态;C为电池容量;Ibat为电池电流;Pbat为电池功率。
1.5 驾驶员模型
驾驶员模型根据车辆需求车速和实际车速的偏差控制加速踏板和制动踏板的大小,使得行驶车速跟随目标车速。该模型采用PID控制,即通过调整上述车速偏差、车速偏差变化率和车速偏差的积分的增益系数(比例kp,积分ki,微分kd)的大小达到车速跟随的目的,调整公式如下:
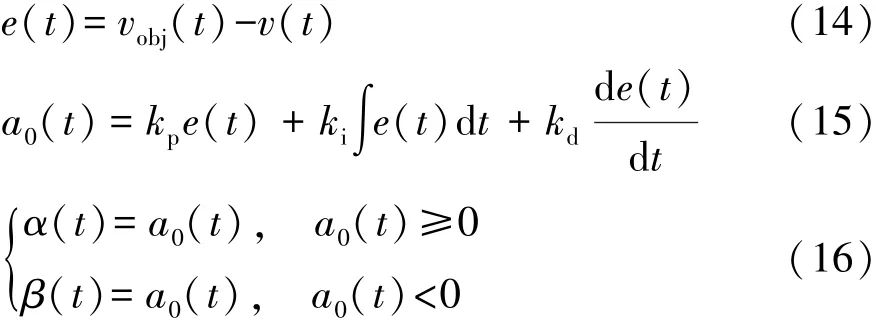
式中:e(t)为车速误差;vobj(t)为目标车速;v(t)为实际车速;α(t)为加速踏板开度信号;β(t)为制动踏板开度信号;a0(t)为PID控制信号。
2 构建DL-MOPSO算法的ECMS优化模型
2.1 ECMS控制算法
ECMS控制思想为:根据整车的实际驾驶员请求功率,在发动机和电机的功率范围内合理分配发动机和电机的实际输出功率,使得发动机瞬时燃油消耗率me和电机消耗电量的等效燃油消耗率mm的总和最小,即

式中:mequ(t)为t时刻系统总燃油消耗率;me(t)为发动机燃油消耗率,可由发动机模型求得;mm(t)为电机消耗电量的等效油耗。mm(t)计算公式为

式中:Pm(t)为t时刻电机的功率;HL为汽油质量热值常数;ηdis(t)和ηchg(t)分别为t时刻某种功率分配方式时电池放电和充电的效率;λdis和λchg分别为驱动和发电模式时放电和充电等效因子,其值与行驶工况类型有关。
由于单纯的ECMS不能很好地维持电池SOC平衡,因此引入惩罚函数对等效油耗进行修正,使其维持在目标SOC附近。具体原则为电池SOC高于目标SOC值时,惩罚系数小于1,通过惩罚系数降低电机消耗电量的等效油耗,使控制策略更倾向于使用电能;电池SOC低于目标SOC值,惩罚系数大于1,通过惩罚系数增大电机消耗电量的等效油耗,使控制策略更倾向于使用燃油,惩罚函数如下:

式中:ψ(SOC)为惩罚系数;SOCtar为目标 SOC值;SOChigh和SOClow分别为SOC维持范围的上下限。修正后的充电和放电等效因子可分别表示为

将式(18)中等效因子 λdis和 λchg替换为 λ∗dis和,同时考虑t时刻制动能量回收功率P(t)对电reg机消耗的功率进行补偿,则修正后电机消耗电量的等效燃油消耗率计算公式如下:

2.2 内外层嵌套ECMS优化问题提出
ECMS的目标函数是使系统总等效燃油消耗量最小,但若仅考虑总等效油耗,必然导致电池电量难以保持平衡。从维持电池电量平衡的角度出发,应使SOC终止值与目标值差值最小。因此ECMS的优化是一个多目标优化问题,即保持总等效燃油消耗量和SOC终止值与目标值差值同时最小。从ECMS的计算流程可以看出,在计算系统总等效燃油消耗量时,主要变量为充电等效因子、放电等效因子和分配的电机功率。而对于某一行驶工况而言,充电等效因子和放电等效因子是一对常数,分配的电机功率是随着行驶功率需求变化而不断变化,因此既要寻找该行驶工况下最优充放电等效因子,又要获得该充放电等效因子下发动机和电机最优功率分配方式。所以上述ECMS的多目标优化函数是一个涉及内外层嵌套优化的不连续优化问题,基于梯度的最速下降法、共轭梯度法等传统优化方法难以有效解决该问题,而遗传(GA)算法,多目标粒子群优化(MOPSO)算法等仿生算法虽不受优化问题的连续性限制,但并不能同时满足内外双层的优化目的,故也无法直接用于求解内外层嵌套优化问题。因此,应设计出一种不受优化问题连续性限制的算法,用于求解上述多目标优化问题。本文中基于多目标粒子群优化算法(MOPSO),设计出一种新颖的内外层嵌套的双层多目标粒子群优化(DL-MOPSO)算法,用于解决上述不连续的内外层嵌套优化问题。DLMOPSO算法由内层MOPSO算法和外层MOPSO算法嵌套而成。其中,内层MOPSO算法用于计算某一对充放电等效因子下,该行驶工况需求功率变化时发动机和电机最优功率分配方式,外层MOPSO算法用于寻找该行驶工况对应的最优充放电等效因子,并通过Pareto解集前沿的更新建立内外层算法之间的联系,以保证外层MOPSO算法对充放电等效因子的不断寻优,进而可解决不连续的内外层嵌套优化问题。
2.3 内外层嵌套ECMS优化算法
DL-MOPSO算法流程图如图2所示。图中外层MOPSO算法的收敛条件包括两个:最大迭代次数;连续30次迭代,无新的Pareto解保存到外部归档集。满足两个条件其中之一,则DL-MOPSO算法停止。

图2 DL-MOPSO算法流程
DL-MOPSO算法的基本步骤如下。
若已知下游断面水位Z下,按公式推算上游一断面水位Z上,该水位对下一个流段来讲,又是下游水位。循环上述步骤,可依次求出上游各断面水位。
(1)设置外层MOPSO算法的种群粒子个数为250,即第m代外层种群为 X(m),X(m)=[,,…,,…,](m为外层算法迭代次数,设置为100,初始值为1)。
(3)设置内层MOPSO算法的种群粒子个数为250,即第 n 代内层种群为 un,un= [,,…,,…,],(n为内层算法迭代次数,设置为100,初始值为1)。
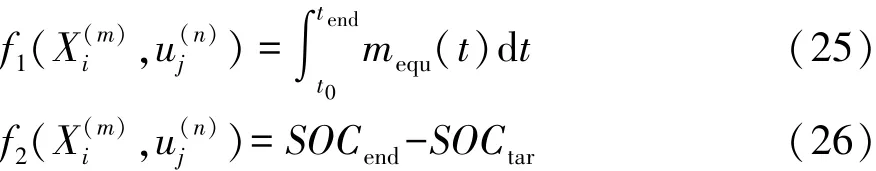
(5)j=j+1,如果 j>250,则跳转至步骤(6),否则,跳转至步骤(4)。
(6)n=n+1,如果 n>100,则跳转至步骤(8),否则,跳转至步骤(7)。
(7)内层粒子的位置更新公式:

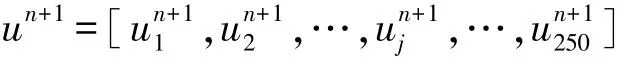
跳转至步骤(4),并更新MOPSO算法外部归档集中的Pareto解集。
(8)i=i+1,如果 i>250,则跳转至步骤(9),否则,跳转至步骤(2)。
(9)m=m+1,若满足收敛条件,则跳转至步骤(11),否则,跳转至步骤(10),收敛条件如下:
a.m>250;
b.连续30次迭代,无新的Pareto解保存到外部归档集。
(10)外层粒子的位置更新公式:

式中参数解释同内层。得到新的外层种群:
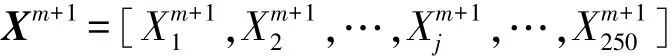
跳转至步骤(1)。
(11)输出Pareto解集前沿。
2.4 约束条件
在双层MOPSO算法寻优过程中,需要对涉及的变量进行约束,包括发动机功率、电机功率和电池SOC。诸多ECMS的研究中,对上述参数的约束只考虑最值问题,并未考虑转速状况和行驶功率需求,
(5)j=j+1,如果 j>250,则跳转至步骤(6),否则,跳转至步骤(4)。
(6)n=n+1,如果 n>100,则跳转至步骤(8),否则,跳转至步骤(7)。
(7)内层粒子的位置更新公式:

式中:ω为惯性权重;r1和r2为分布于[0 1]区间的随机数;n为当前迭代次数;p为个体最优粒子位置;g为全局最优粒子位置;c1和c2为常数;v为粒子速度;u为粒子位置。得到新的内层种群:因此需要对约束条件进行改进,约束如下:
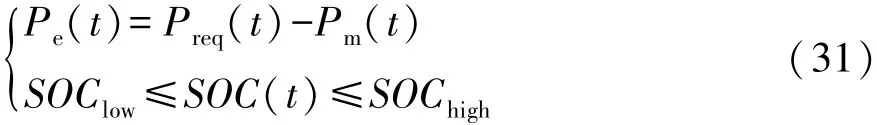
式中:Pe(t)为t时刻发动机的功率;Preq(t)为t时刻行驶工况的需求功率。对电机和发动机功率的约束具体分以下两种情况:
(1)当Preq(t)>Pm_max(nm(t))时,

(2)当Preq(t)≤Pm_max(nm(t))时,

式中:Pm_max(nm(t))为t时刻转速nm时电机所能提供的最大功率,即最大驱动功率;Pm_min(nm(t))为t时刻转速nm时电机所能提供的最小功率,即最大发电功率;Pe_max(ne(t))为t时刻转速ne时发动机所能提供的最大功率。
3 DL-MOPSO算法求解
本文中在Matlab/Simulink平台搭建ECMS控制策略模型,并将控制策略模型嵌入已建立好的整车模型,顶层控制策略和整车模型如图3所示。利用Matlab编写充放电等效因子和功率分配方式同时优化的DL-MOPSO算法程序,优化过程中通过函数不断调用Simulink整车和控制策略模块,获得适应度函数值。参考文献[13]~文献[18],充电等效因子和放电等效因子的优化范围设置为[0,5],工况选择燃油经济性评价常用的NEDC工况。电池SOC上下限分别为0.7和0.6。最终得到多目标优化的Pareto解集前沿。这里分别列举优化过程中随机保存的某一组外层粒子时得到的内层Pareto解集和最终DL-MOPSO算法优化得到的Pareto解集前沿,分别如图4和图5所示。由图4可以看出,该内层解集中适应度函数f1的值均较大,因此该外层粒子对应的内层解集均不保存在外层解集前沿中。由图5可以看出,最终保存的解集中,油耗范围为5.6~5.8,而SOC终值与目标值之差变化范围为0~0.05。Pareto解集前沿由Pareto解构成,设计人员仍需从解集前沿中选出最优解。本文中通过构建评价函数,用于选择最优解。
MOPSO中粒子的拥挤距离越大,该粒子被选为最优粒子的概率也越大[19],将上述Pareto解集前沿按拥挤距离从大到小排序,取前30个Pareto解所对应的f1和f2,构建总评价函数:
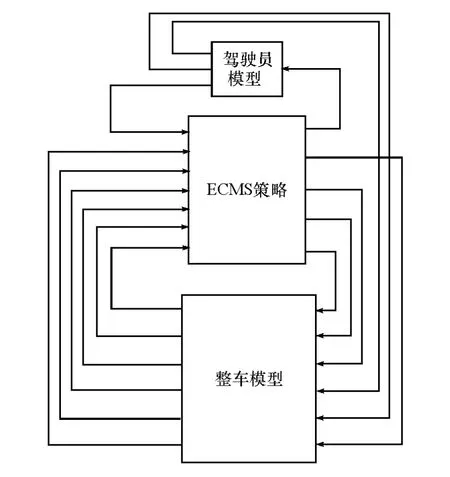
图3 整车及控制策略顶层模块

图 4 λchg=2.1,λdis内层 Pareto解集

图5 DL-MOPSO算法输出的解集前沿

式中:∂1和∂2为权重系数;γ为评价指标。依据上述30个Pareto解的f1和f2,采用直接加权法[19],可计算权重系数∂1和∂2。采用该方法取权重系数时,当某适应度函数的数值变化范围愈宽时,权重系数就取较小值;当数值变化范围愈窄时,权重系数就取较大值,因此该方法可以达到平衡各分适应度函数值数量级的作用。 求得 ∂1=143.885,∂2=1810.938。分别将30个Pareto解的f1和f2带入式(32)中计算。评价函数γ值越小,表明在整车仿真中,燃油经济性和SOC偏差总体水平越好。最小γ=836.243,所对应的外层解为 λchg=1.549,λdis=1.202,所对应的内层解,即该充放电等效因子下发动机和电机最优功率分配方式如图6和图7所示。
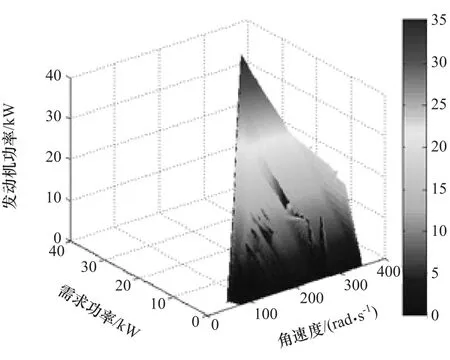
图6 发动机功率分配方式
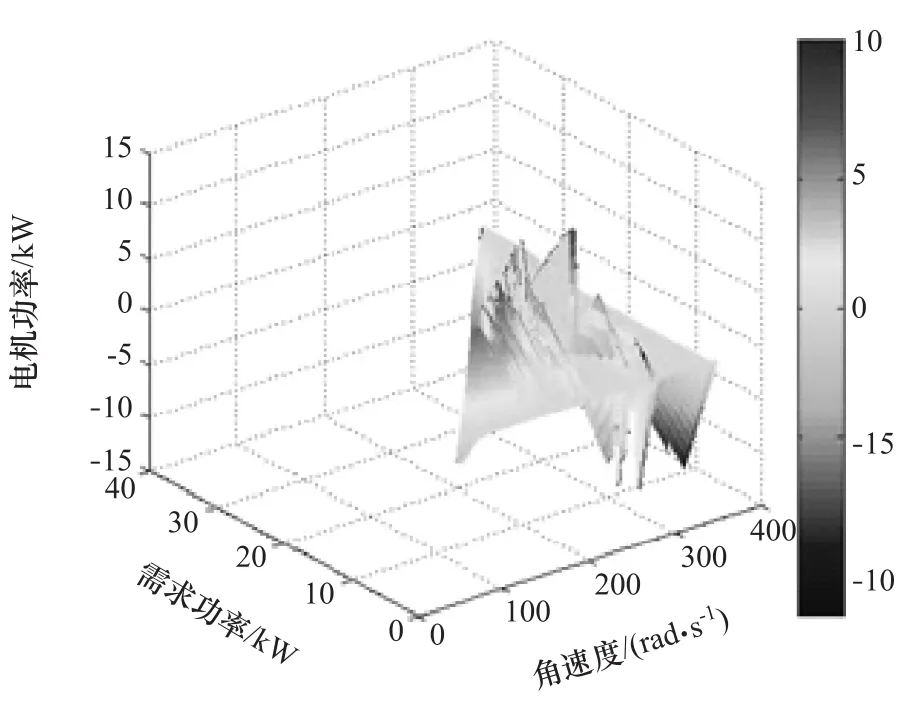
图7 电机功率分配方式
4 基于DL-MOPSO算法优化的ECMS效果分析
为了进行对比分析,分别将传统ECMS和经过DL-MOPSO算法优化的ECMS封装成模块嵌入整车模型中,初始SOC设定为0.63,电池SOC上下限分别为0.7和0.6,仿真工况为NEDC工况。传统ECMS中利用穷举法获得的最优充放电等效因子为λchg=2.250,λdis=2.130。 两种情形下仿真过程车速跟随情况及主要部件工作状况如图8~图10所示。由图8可知,两种情形下ECMS都满足车辆需求功率,使得实际车速与目标车速基本吻合,车速跟随误差较小。

图8 两种情形下车速跟随情况

图9 发动机输出功率
由图9和图10可见,在NEDC工况的前4个ECE阶段,穷举法获得的ECMS下(以下简称策略1),发动机和电机的输出功率波动较大,而经过DLMOPSO算法优化的ECMS(以下简称策略2)下,发动机和电机的输出功率波动均减小。该阶段需求功率较小,在满足功率需求的前提下,通过寻优,合理地确定ISG电机输出的功率补偿需求功率与发动机功率之间的差值,从而保证发动机工作在中等负荷的最佳燃油经济性区域。而在EUDC阶段,功率需求较大的情况下,策略2则使发动机始终保持较大的功率稳定输出,而ISG电机则起到辅助作用,因此电流波动不大,需求功率减小则对电池充电,需求功率增大则进行助力。而策略1下,发动机输出功率则波动剧烈,进而使得电池输出和输入电流波动剧烈,降低充放电效率,同时发动机也因输出功率剧烈变化而降低燃油经济性。

图10 电机输出功率
由图11可知:策略2累积燃油消耗量为960g,百公里油耗为5.788L;策略1燃油消耗量为1 070g,百公里油耗为6.451L。经过DL-MOPSO算法寻优后,燃油经济性提高10.28%。由图12可知,两种策略下SOC保持性能均较好,但策略2下SOC变化相对平稳,且电池充放电次数减少,有利于提高系统效率和电池寿命。

图11 累积燃油消耗量
5 惩罚系数对ECMS影响分析

图12 SOC变化情况
通过惩罚函数计算得到惩罚系数值,主要用于修正电机消耗电量的等效油耗,调控对电能的使用倾向,维持电量在SOC目标值附近。由图13可知,电池SOC大于SOC目标值0.65时,惩罚系数小于1,降低电机消耗电量的等效油耗,增加使用电能倾向;电池SOC小于SOC目标值0.65时,惩罚系数大于1,增大电机消耗电量的等效油耗,增加使用燃油倾向。相同SOC值时,由于β不同,惩罚力度也不同,等效油耗也不同,进而影响发动机和电机的功率分配,因此需进一步分析不同β值对ECMS的影响。由图13可以看出,随着β不断增大,惩罚系数曲线趋于收敛,因此这里分别以β值为图13中6种情况优化时得到f1和f2两个适应度函数值为例分析,得到的f1和f2结果如图14。

图13 惩罚系数随SOC变化情况

图14 不同β时f1和f2结果
由图14可知,随着β的增大,电池SOC的保持性能越来越好。当β较小时,f1和f2均较大;当β较大时,虽具有良好的电量保持性能,但是整车燃油经济性较差;当β取中间值时,SOC偏差的量级已经很小,且燃油经济性最佳。综上所述,在选择惩罚系数的β参数时,应取中间值,即5或7。
6 结论
(1)将ECMS封装嵌入整车Matlab/Simulink模型中,建立基于PID控制的驾驶员模型,仿真结果表明车速跟随效果良好,车速跟随误差较小。
(2)针对ECMS核心算法的前两个关键部分,以降低燃油消耗量和减小SOC终值与目标值偏差为两个优化目标,提出一种内外层嵌套的DL-MOPSO算法对充放电等效因子和功率分配方式同时进行寻优,得到最优充放电等效因子下任意需求功率时发动机和电机最优分配方式的Pareto解集前沿,并通过直接加权法获得最优解。对寻优结果进行仿真,与传统基于穷举法构建的ECMS相比,燃油经济性提高10.28%,电池SOC具有良好的保持性能且更加稳定。在后续的研究中,将通过在环实验,验证该优化的ECMS具有更好的整车燃油经济性和电量保持性能。
(3)分析了惩罚函数中β参数值对EMCS策略寻优结果的影响。结果表明:随着β值的增大,电池SOC保持性能逐渐增加,但整车燃油经济性先减小再增加,因此β应取中间值5或7。

