同步发电机不同实用模型对暂态稳定极限准确性的影响

宋美红

(中国城市建设研究院有限公司, 北京 100120)

0 引言

暂态稳定性是指电力系统发生大扰动后，发电机功角能够在第一、二个振荡周波内不发生失步的能力[1-2]，该指标对于评估发电机承受电力系统扰动的能力具有重要意义[3-6]。通常在研究电力系统及发电机稳定问题时，采用发电机的实用模型进行仿真计算，而目前发电机的实用模型有两类，均是以发电机Park方程为基础推导得出[6-9]。因此，研究两种实用模型对发电机暂态稳定极限计算结果的影响十分必要。

由于发电机转子存在阻尼绕组、励磁绕组等多个回路，且有些阻尼回路，如汽轮发电机转子，是由整块导电钢构成，因而很难准确获得这些绕组的电感和电阻参数[10-11]。在分析发电机动态过程时通常采用基于瞬态，超瞬态参数的实用模型来描述同步发电机[12-14]。然而，在Park方程到实用模型的推导过程中，由于参数不对等，通常需引入一些假设条件才能推导出相应的实用模型[13-14]。文献[15—16]给出了从Park方程到实用模型的推导过程，得出了两种发电机实用模型的差异；文献[17]通过对比得出了两种实用模型的仿真差异，但是文献中并没有对两种实用模型仿真结果的准确性和适用性进行深入的校核和分析。

为了获得两种实用模型在仿真过程中准确性的差异，采用计及因素更加全面的发电机时步有限元结果作为标准对其进行校核。时步有限元模型以发电机结构为基础，通过计算动态过程中的磁场分布与变化，计及了饱和，交叉磁化和集肤效应等因素的影响[18-20]。文献[21—22]对比了时步有限元仿真结果与试验测试结果，发现两者非常一致。但是时步有限元仿真计算所需资源庞大，计算时间较长，一般不适于大规模电力系统仿真，因此仅用来校核两种实用模型的仿真结果。

文中对比分析了两种发电机实用模型和时步有限元模型的差异。采用假设A实用模型和假设B实用模型计算了发电机大扰动过程和暂态稳定极限，并将其与时步有限元计算结果进行对比，获得了两种实用模型的准确性差异。

1 同步发电机两种实用模型的对比

发电机实用模型是在Park方程的基础上引入两种假设条件得到的。Park方程转子电路方程由4个绕组来描述，分别为直轴励磁绕组f和阻尼绕组D，交轴阻尼绕组g和Q。4个绕组的电抗可表示如下：

(1)

式中:xf,xD,xg,xQ为直轴励磁绕组f和阻尼绕组D、交轴阻尼绕组g和Q的电抗；xfσ,xDσ,xgσ,xQσ为励磁绕组和三套阻尼绕组的自漏电抗；xfD为励磁绕组f和阻尼绕组D之间的互电抗；xgQ为阻尼绕组g和Q的之间的互电抗；xfDσ为励磁绕组f和阻尼绕组D之间的互漏电抗；xgQσ为阻尼绕组g和Q的互漏电抗；xad和xaq为直轴和交轴的电枢反应电抗。

第一种假设条件通常称为假设A，满足如下参数关系：

(2)

式中:xaf,xaD,xag,xaQ分别为电枢绕组与励磁绕组f、阻尼绕组D、g、Q的互电抗。

根据式(2)和文献[8]中的参数定义得到假设A实用模型如下：

(3)

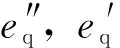
第二种假设称为假设B，参数满足如下关系：

(4)

根据式(4)和文献[9]中的参数定义得到假设B实用模型如下，其中x1为定子漏电抗：

(5)

2 场-路耦合时步有限元模型

2.1 时步有限元方程

在麦克斯韦方程组的基础上，列写同步发电机电磁场方程如下所示：

(6)

式中：A为矢量磁位；μ为磁导率；Jsource为源电流密度；Je为感应电流密度。

源电流密度包括定子绕组电流密度Jst与励磁绕组电流密度Jf，可通过式(7)求得。

(7)

式中：Ns和Ss分别为定子绕组匝数和截面积；Nf和Sf为励磁绕组匝数和截面积；a为定子绕组并联支路数；Is为定子电流的矩阵形式；if为励磁电流。

发电机动态过程中，转子阻尼绕组中感应电流的大小取决于切割磁场的变化快慢和阻尼绕组的电导率，可表示为：

(8)

式中：σd，σs，σr分别为发电机转子大齿导条、转子槽楔与转子铁心的电导率。

将式(8)的感应电流密度与磁场方程(6)相结合，可得：

(9)

式中：K为刚度矩阵；Cs和Cf分别为定子电流和励磁电流的关联矩阵；Dd，Ds，Dr分别转子阻尼电流的关联矩阵。

发电机定子绕组和励磁绕组的电压方程为：

(10)

式中：Ul为定子电压，其矩阵形式可表示为[UA,UB,UC]T；Is为定子电流，其矩阵形式可表示为[iA,iB,iC]T；Rs和Ls为定子电阻和漏电感，可表示为diag[ra,ra,ra]和diag[ls,ls,ls]；lef为轴长；rf为励磁电阻；ls和lf为定子绕组和励磁绕组的端部漏抗。

结合磁场方程(9)和定、转子绕组电路方程(10)，可得发电机场-路耦合时步有限元方程：

(11)

由于时步有限元针对发电机内部实际的电磁场进行计算，因而可以准确的计及励磁绕组和转子阻尼绕组之间的互漏磁场。除此之外，对于发电机动态过程中转子铁心，导电槽楔和转子大齿导条中涡流所产生的阻尼以及涡流的集肤效应、交叉磁化等非线性因素均进行了准确计及。

2.2 时步有限元模型的试验验证

在发电机动态分析中，以时步有限元计算结果为标准响应校核实用模型的结果。为了验证时步有限元模型的准确性，在一台2极7.5 kW的同步发电机模型机上进行试验。该模型机如图1所示，采用直流电动机作为原动机将模型机拖动到同步转速，并在励磁绕组上施加空载励磁电流，将机端三相突然短路，并测试定子电流与励磁电流变化。将实验和仿真结果进行对比，如图2所示，从中可以看出仿真与实测曲线基本一致。

图1 7.5 kW 模型机Fig.1 7.5 kW model machine

图2 7.5 kW模型机的空载突然短路试验和仿真对比Fig.2 Comparison between the simulation result of T-S FEM and testing of 7.5 kW Model machine

3 同步发电机不同模型计算的暂态稳定极限对比

3.1 系统仿真模型

文中采用单机-变压器-双回线-无穷大系统来研究不同发电机模型对暂态稳定极限仿真结果的影响，系统的仿真模型如图3所示。发电机模型分别采用时步有限元模型和基于电机参数的两种实用模型。图3中：UG为发电机的机端电压；UT为变压器高压侧电压；US为电网电压。

图3 系统仿真模型Fig.3 System simulation model

文中采用的发电机为QFSN-2-300 MW型同步发电机，变压器为Dy11联结组别的理想变压器。变压器与无穷大系统之间的线路电抗决定了系统的连接强弱，系统连接强弱不同，其暂态稳定极限相差较大，因此文中对比了线路电抗为0.25 p.u.的强连接系统和0.5 p.u.的弱连接系统情况下，3种发电机模型所计算的暂态稳定极限。

3.2 不同模型计算的大扰动结果对比

发电机的暂态稳定极限是指其发生大扰动后的稳定问题，因此首先计算了发电机的大扰动过程，对比分析了时步有限元、假设A和假设B模型所计算的大扰动过程的差异。文中设定的大扰动包括2个过程：(1) 图3所示F点三相突然接地短路；(2) 短路持续0.1 s后故障线路切除。采用3种模型分别计算了系统强连接和弱连接时的动态过程，结果如图4所示。

图4 3种发电机模型计算的大扰动功角曲线Fig.4 The large disturbance curves calculated by three synchronous models

从图4可以看出，3种发电机模型计算的功角曲线均存在差别，且系统弱连接时，这种差别更加明显。同时，从图4也可以看出，假设A模型计算结果与时步有限元结果接近，而假设B模型的计算结果与时步有限元相差较大。

3.3 不同模型计算的暂态稳定极限对比

逐渐增加大扰动前发电机稳态运行时的输出有功(P0)，采用3种模型计算发电机在输出不同有功功率时的大扰动过程，获得发电机大扰动后能够维持稳定运行的暂态稳定极限，此时对应的稳态输出功率称为极限功率(Plim)。

系统强连接时，3种发电机模型计算发电机极限功率的过程如图5所示。

图5 不同输出功率下3种模型计算的大扰动功角曲线Fig.5 The large disturbance curves calculated by three synchronous models under different P0

随着发电机扰动前输出功率的增加，当P0增加到421.14 MW时，假设B 模型计算的功角失去稳定；当P0增加到426.67 MW时，假设A模型计算的功角失去稳定；当P0增加到437.42 MW时，时步有限元模型计算的功角失去稳定。由此可以得出时步有限元、假设A和假设B模型计算的暂态稳定极限分别为437.42 MW，426.67 MW和421.14 MW。系统弱连接时，3种发电机模型计算发电机极限功率的过程如图5所示。从图5可以得出时步有限元、假设A和假设B模型计算的暂态稳定极限分别为367.34 MW，360.16 MW和356.06 MW。

按照相同的计算方法，分别得到了系统强弱连接情况下，80%励磁时3种发电机模型的暂态稳定极限，结果如表1和2所示，其中ξ为实用模型计算的极限功率相对于时步有限元计算结果的偏差。

表1 系统强连接时3种模型计算的暂态稳定极限Tab.1 Transient stability limits calculated by three synchronous models under different initial condition MW

表2 系统弱连接时3种模型计算的暂态稳定极限Tab.2 Transient stability limits calculated by three synchronous models under different initial condition MW

从表中可以得出：(1) 无论系统强弱连接还是励磁条件改变，假设A模型计算的暂态稳定极限均与时步有限元结果最接近，而假设B模型计算结果与时步有限元模型结果则相差较大，相差最大的极限功率为16.28 MW。(2) 额定励磁下，实用模型计算结果与时步有限元结果相差较大，而80%励磁时则相差较小。系统强连接时，实用模型计算的暂态稳定功率与时步有限元结果相差较大，系统弱连接时相差较小。

4 结语

文中通过研究实用模型与时步有限元在计算同步发电机大扰动过程和暂态稳定极限时的差异，得出如下结论：

(1) 假设A模型计算的大扰动特性及暂态稳定极限与时步有限元结果最接近，而假设B模型计算结果与时步有限元模型结果相差较大，因此可以得出，在计算大扰动及暂态稳定极限时，假设A模型更加准确。

(2) 在计算同步发电机大扰动过程时，系统强连接时实用模型结果与时步有限元相差较小；在计算同步发电机暂态稳定极限时，系统弱连接时实用模型计算结果与时步有限元结果相差较小。