敏感负荷对含新能源配网规划的影响

赵 芳, 杜兆斌

(华南理工大学电力学院，广东 广州 510640)

0 引言

大规模风电、太阳能等可再生能源发电功率波动会造成电压、频率波动和电能质量问题[1]，其高比例入网会造成一定程度的电压波动，增加网络的不确定性。相同功率因数时，光伏电源的渗透率越高，引起的节点电压波动幅值也越大，同时若注入的无功功率超过局部无功负荷的需求，也会引起潮流反向[2]。如今异步电机在发电场应用仍比较普遍，运行中会消耗电网中的无功功率，在无功容量不足的情况下，会降低整个配电系统的电压值[3-4]。

另一方面，计算机、可调速电机、直流电机驱动、交流接触器、可编程逻辑等设备大量投入使用，其运行状态极易受到电压变化的影响，往往几个周波的电压暂降或供电中断都会导致设备运行异常，严重时导致设备故障，造成大量的损失[5-7]。考虑到电压敏感型负荷的比重在逐渐增加，配网规划现须更加重视其供电可靠性。这些都对电网的运行和规划提出了新的要求。从长远来看，现有的网架规划方案将可能满足不了未来负荷发展的需求。

目前，国内外针对负荷的电压敏感性以及含分布式能源发电的配电网规划都各有不少研究。文献[8]对可调速驱动装置的电压敏感度进行了分析，并绘制了不同电压暂降类型、电容大小的电压耐受曲线，但未考虑敏感负荷在不确定区域的损失概率。文献[9]用电压耐受曲线和负荷敏感度随机模型表征负荷对电压凹陷的敏感特性，提出了敏感负荷电压凹陷敏感度的随机估计方法。文献[10]以电压暂降严重性指标为依据，提出一种基于最大熵原理的负荷电压暂降敏感度评估方法，该方法对样本数依赖性小，无需主观假设，但文献[9—10]均未考虑电压凹陷的起始点和相角跳变等因素对负荷电压凹陷的敏感度的影响。文献[11—12]考虑了大量分布式电源接入，其出力的波动、间歇和随机特性对配电网风险评估造成的影响，建立了基于配电网运行风险指标的配电网评估模型。文献[13—15]分析了分布式电源容量对配电网的影响，以维护、投资费用最低为目标函数，建立了配电网规划多目标模型，但是规划中缺少对配电网风险因素的考虑。文献[16]提出了综合考虑配电网规划与系统运行的优化模型，将负荷丢失成本作为评价配电网可靠性的指标，但该指标不可量化计算，评价精度有待提高。由此可见，现有配电网规划都未考虑负荷的电压敏感特性对配网规划的影响，规划模型对负荷的描述可进一步发展。

本文以变频调速电机型负荷为代表分析电压敏感型负荷对配电网规划的影响。首先在仿真软件MATLAB/SIMULINK上建模，研究变频调速电机对电压凹陷的耐受能力，并通过电压敏感度曲线和负荷敏感度随机模型确定其在电压耐受曲线不确定区域的负荷损失概率。然后分析了配网中大量敏感负荷对安全性和经济性的影响，论述了将敏感负荷损失引入配电网规划模型中的必要性，最终对配电网的网架规划模型做出了改进和案例展示。

1 敏感负荷的电压敏感特性

应用MATLAB/SIMULINK建模对典型用电设备(如变频调速类设备)的电压耐受能力进行分析，得到其电压耐受能力。为后续电压凹陷造成负荷损失的分析和评估提供数据支持。

1.1 变频调速电机的电压敏感性仿真

变频器广泛应用于电机调速，与控制系统及异步电动机一起构成变频电机的主要组成部分，变频方式多采用交-直-交变换，即先把工频交流电源通过整流器转换成直流电源，然后通过控制系统和逆变器把直流电源转换成频率、电压均可调节的交流电源[17]。电压凹陷可能影响变频调速器的正常运行，导致电机异常，对生产过程造成损失。建立变频电机的MATLAB/SIMULINK仿真模型，交流调速控制方式采用直接转矩控制方式，该系统的控制部分由PI调节器、两相/三相坐标变换、PWM脉冲发生器等环节组成。采用的电动机为MATLAB自带模型，仿真参数为：Rs=0.214 7 Ω，Rr=0.220 5 Ω，Ls=Lr=0.009 91H，Lm=0.064 19 H，J=0.102 kg·m2，np=2，UN=400 V，fN=50 Hz。仿真模型如图1所示。

图1 变频电机的仿真模型Fig.1 Simulation model of frequency converter

影响变频器的电压暂降敏感度的主要因素有负载转矩、电机转速和电压暂降类型。根据图1的仿真模型对直接转矩控制的三相异步电动机进行仿真研究，得到变频电机的转差波形，如图2所示。仿真定转速为1420 r/min时的空载启动，启动后0.1 s时加额定负载TL=100 N·m，在0.2 s时设置三相电压暂降幅值分别为0.6 p.u.，0.7 p.u.，0.8 p.u.和0.9 p.u.，仿真时长为0.4 s。

若要求转速不得低于1400 r/min，即转差s不得大于0.066，该变频电机的电压暂降幅值和对应的临界凹陷时间如表1所示。

1.2 部分代表性设备的电压耐受能力

各类负荷在电网事故中对电能质量的敏感程度各有不同，通过现场调研和文献查阅，得到几种典型敏感负荷的电压耐受能力:

(1) 计算机。当系统电压降至60%，持续时间达到240 ms时，其正常运行会受到影响，导致数据丢失、重启、关机等。

(2) 精密机械工具。电压低于90%且持续时间超过2～3个周期，就会停止工作。

(3) 直流电机。当电压降低到88%时，直流驱动能力将开始减弱，直流驱动的生产线将会减速，导致出现不合格产品；当电压低于80%时，直流电机就会被跳闸，生产线会停止运转。

(4) 变频调速器。系统电压低于70%并持续超过120 ms，电机自动切除。

2 电压波动引起的敏感负荷损失

试验表明，敏感负荷如可编程逻辑控制器(PLC)、计算机(PC)、交流调速器(ASD)的电压耐受曲线(VTC)一般呈矩形[13]。不同的负荷类型对电压凹陷的敏感度也有所差异，同种负荷也会受到环境温度、安装位置、运行时间和保养频度等因素影响，因此负荷的电压耐受曲线存在着不确定区域。当敏感负荷遭受该区域范围内的电压暂降时，负荷能否继续正常工作并不能完全确定，而是存在一个概率。本文以这个概率作为敏感度的指标,结合电压暂降平均水平，可评估敏感负荷受扰的经济损失。

图2 变频电机转差变化曲线Fig.2 Slip curve of variable frequency motor

电压幅值/p.u.电压凹陷时间/ms0.9198.30.8183.30.7126.40.636.6

图3中，T为电压凹陷的持续时间；U为电压幅值；Umin和Umax分别为实际负荷VTC的电压幅值最小值和最大值；Tmin和Tmax分别为实际负荷VTC持续时间的最小值和最大值。曲线1的外部区域(U>Umax且TTmax为故障运行区；曲线1、2之间为不确定区域。

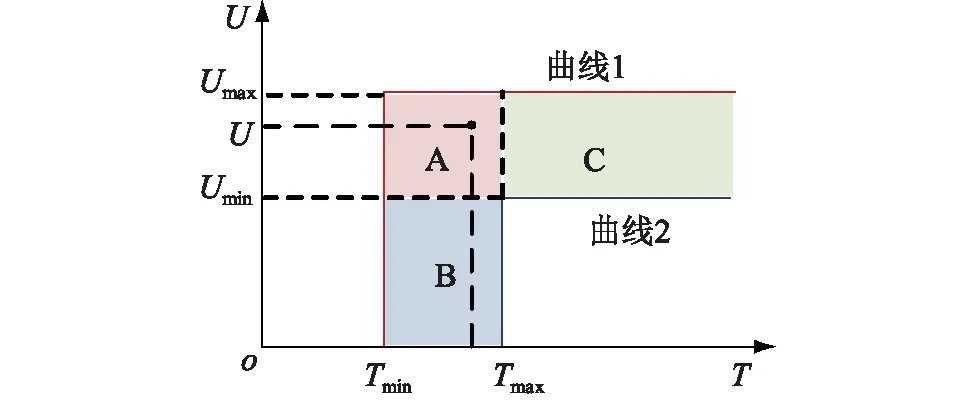
图3 负荷电压耐受曲线Fig.3 Load voltage tolerance curve

实际运行中负荷母线的U和T是随机变量，用正态分布概率密度函数表征U和T的随机性。假设B区和C区内随机变量T和U的概率密度分别为fx(T)和fx(U)，则A区内随机变量T和U的联合概率密度函数及VCT 曲线的标准概率模型如下[9,18]：

fx,y(T,U)=fx(T)fy(U)

(1)

(2)

(3)

(4)

式中:σ1,σ2分别为负荷VTC在不确定区域的分布密度；T0,U0分别为VTC中T和U概率最大处的持续时间和电压幅值。在不确定区域内，VTC 的顶点均在A区，如果已获得母线实际电压幅值和持续时间，则根据不同负荷的 VTC 的变化范围可确定T0,U0，σ1,σ2，将其代入式(1—4)即可得到不确定性区域内负荷VTC的随机估计模型。对fx,y(T,U)求定积分可求出负荷在电压耐受曲线不确定区域范围内的故障概率。

以变频调速类负载为例，Umax，Umin，Tmax，Tmin在VTC中的数值分别为1 p.u.，0.7 p.u.，120 ms，0 ms。代入VCT 曲线的标准概率模型中，得到VTC在A区的概率分布，见图4。

图4 变频调速器的VTC在A区的概率分布Fig.4 Occurrence probabilities of voltage tolerance characteristics of frequency converter in region A

对fx,y(T,U)求定积分，得到变频调速器类负载在VTC不确定区域范围内的故障概率如表2—4所示。

表2 变频调速器的VTC在A区的损失概率Tab.2 Loss probability of frequency converter in region A

表3 变频调速器的VTC在B区的概率分布Tab.3 Loss probability of frequency converter in region B

表4 变频调速器的VTC在C区的概率分布Tab.4 Loss probability of frequency converter in region C

由表2—4可以看出，假若电压降幅和电压凹陷持续时间同时接近极限值时，敏感设备故障的概率极大。同样，假若两个变量同时接近安全值，那么故障概率将会非常小，而只有一个变量接近安全值的情况下也存在一定几率发生故障。

3 考虑负荷损失的配网规划模型

3.1 敏感负荷对配网的影响

电压凹陷发生时，敏感负荷单个设备或元件的故障可能使整个生产线的产品报废，给用户带来极大的经济损失[19-20]。除此之外，大量敏感负荷还会对配网的以下几个方面产生影响。

(1) 负荷预测。敏感负荷的产生负荷损失以及负荷恢复期间，会增大超短期负荷预测值与实际负荷值的偏差，使得用户用能需求评估不准确。

(2) 无功规划。对含大规模分布式电源接入的电网来说，电源接入位置和容量会影响到母线电压水平[21]，因此敏感负荷对电压质量的高要求会影响到无功电源的建设。

(3) 电力平衡。大量敏感负荷的突然损失及负荷恢复会造成瞬间的电力不平衡。

(4) 投资估算。负荷损失可能导致严重的经济损失。此外，在响应用户电能质量要求时，也影响到调压稳压设备的配置，从而导致投资成本的增加。

从以上分析可以看出，敏感负荷的电压耐受度对电网的影响主要体现在安全性和经济性方面，因此在未来进行网架规划时，需要考虑敏感负荷对电压的特殊要求。故在风险规划的基础上，追加考虑敏感负荷损失造成的经济代价，对现有的网架规划模型进行扩展和改进。

3.2 配电网规划的数学模型

配网规划时，在经济性、稳定性的基础上考虑运行风险、不同天气状态对网络的影响等因素。风险因素包括切负荷和电压越限两个方面[3,18]，本文在此基础上增加了电压波动导致的负荷损失因素。根据正常和恶劣天气条件下的线路设备故障率，采用系统切负荷期望值对切负荷量进行计算，电压越限惩罚函数作为电压越限评价指标。敏感负荷的损失概率和损失量的计算方法为：考虑不同天气对发电系统输出功率的影响，建立分布式发电系统的概率模型[22]，得出新能源在连续时间段内的输出功率概率。依次计算潮流，得到稳态电压分布和电压幅值波动的影响，进而得到电压波动曲线。在得到敏感负荷的VTC顶点后，将其代入到联合分布密度函数(1)中，通过确定函数的积分结果，计算出电压凹陷影响下的负荷损失概率。根据电压波动曲线，确定各类敏感负荷的负荷损失概率，得出敏感负荷损失量及其导致的经济损失。

3.2.1 目标函数

文中配电网风险规划模型以待选路径及回数作为决策变量，在保证合理风险水平的前提下，综合考虑在规定年限内的经济投资收益最大值。传统风险规划模型未考虑敏感负荷损失量，其目标函数表达式为[3]：

maxF=FPV-FL-FEC-FV

(5)

目标函数中的各分量表达式如下：

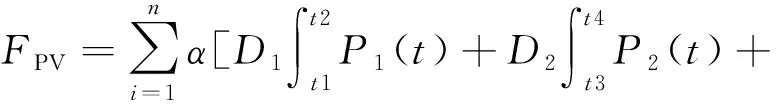
(6)

(7)

(8)

(9)

式中：F表示配电网规划收益目标函数，求取其最大值；FPV表示配网规划时的分布式电源总投入在一定时期内的收益；FEC表示故障线路设备引起的系统切负荷成本；FV表示电压越限惩罚成本；FL表示配电网新增线路的投资成本；α表示平均电价；Di，Pi分别代表在不同天气情况下的时间和发电特性曲线；CDG表示分布式发电设备建设成本；n表示分布式发电设备计划发电年限；FL表示规划线路造价成本；r表示贴现率；m表示规划期限内线路设计寿命；nl表示增加线路数量；Li表示第i条线路长度；Cli表示第i条线路单位长度价格；Pk为第k种预想故障发生的概率；Ck为因第k种预想故障发生而丢失负荷量；E为所有的预想事故集；β表示单位负荷损失量的平均成本。

考虑敏感负荷损失因素，对风险规划模型进行改进，建立目标函数：

maxF=FPV-FL-FEC-FV-Fl

(10)

Fl的表达式为：

(11)

3.2.2 约束条件

(1) 功率平衡约束：

∑pij=PGi-PDi

(12)

(2) 线路潮流约束：

(13)

(3) 线路回路数目上下限约束及整数约束：

(14)

3.2.3 风险规划流程图

考虑天气因素对配电网运行风险和新能源出力的影响，经过本节所述改进风险规划评估指标进行评估，得到合理的规划方案，改进的计算流程如图5所示。

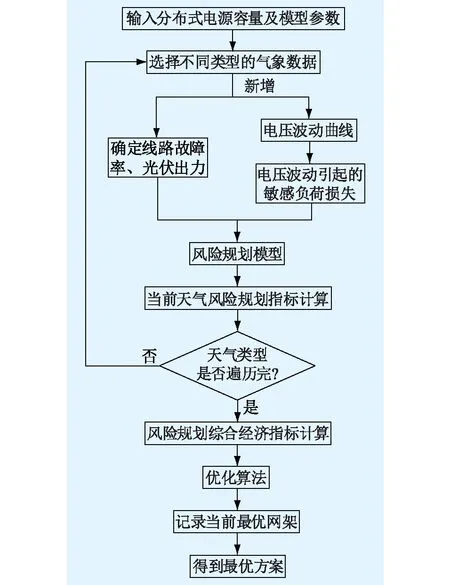
图5 规划流程Fig.5 Planning flow chart

4 算例

本节以配电网6节点系统为例，验证提出的考虑敏感负荷损失配电网风险规划方法的可行性和有效性。配网长期运行时，配网产生的电压暂降时间都足够长[23]，故主要考虑敏感负荷在C区的损失概率。6节点系统作为一个配电网小型测试系统，节点3为平衡节点，其余皆为PQ节点，其中节点1接有发电机，节点6上安装了光伏装置。具体数据见表5和表6，其中，光伏装置投资费用11.5 元/W。

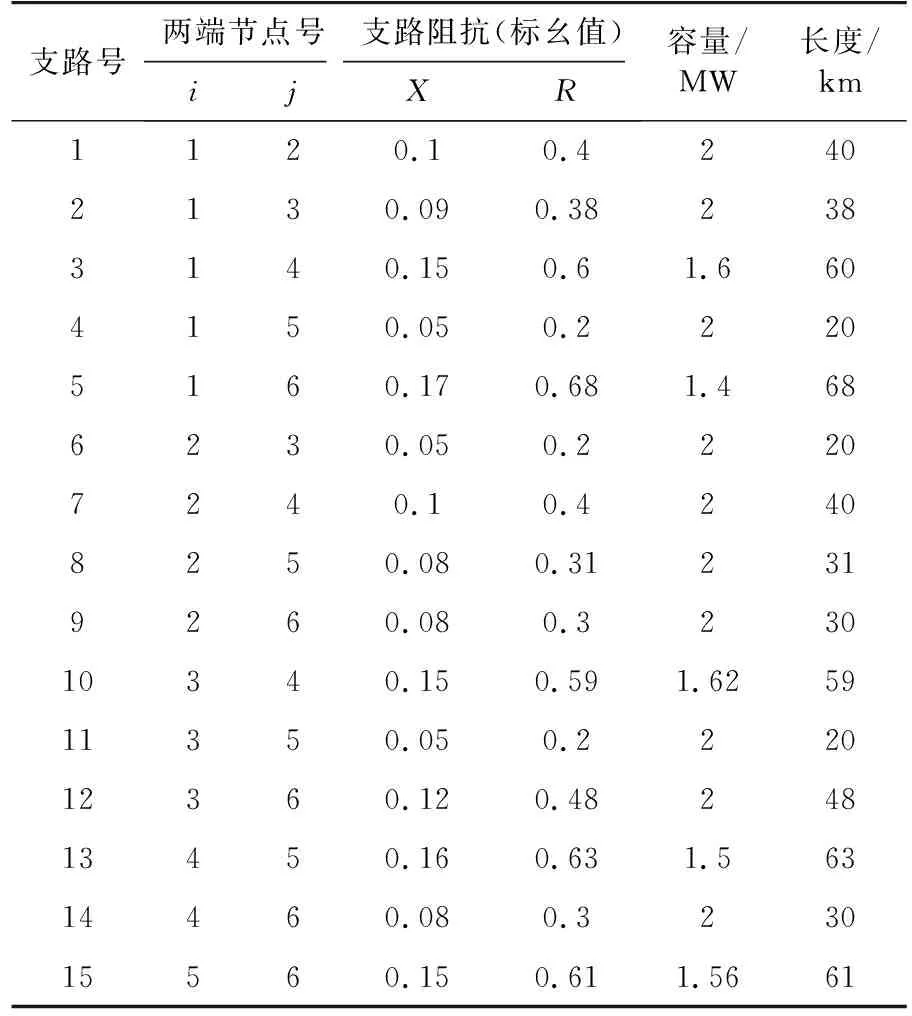
表5 支路数据Tab.5 Branch data

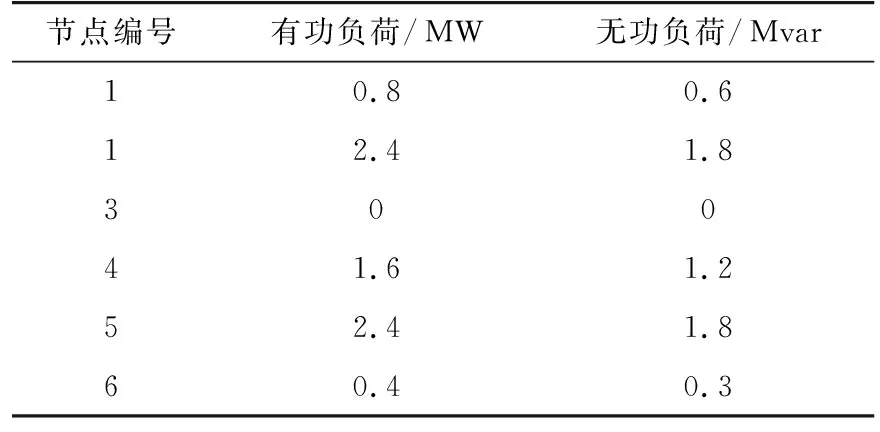
表6 节点数据Tab.6 Bus data

每度电发电收益1.15 元，规划年限为20 a，为了分析方便，算例假设节点1,2,4,5,6存在敏感负荷，且容量均为各节点总负荷的50%，并选用我国南方某区域呈较接近正态分布的光伏出力数据，光伏渗透率约30%。

图6中，6节点之间的15条可增线路走廊，其中实线表示现有网架，为4条单回线路。在现有网架的基础上，每条线路走廊最多可扩建2回线路。采用粒子群算法对规划模型进行求解，将粒子位置用支路回数的数组来表示，粒子速度用各走廊线路回数变化值矢量表示。经过500次迭代，得到不考虑敏感负荷损失时的最优网架规划结果见图7(a)，考虑敏感负荷损失的最优网架规划结构见图7(b)。

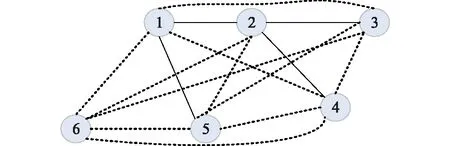
图6 6节点网络拓扑Fig.6 6 nodes network topology

图7 网架规划结构Fig.7 Grid line planning topology

当考虑敏感负荷损失因素时，网架规划方案与用不考虑敏感负荷损失得出的方案相比，虽然网损和线路投资总费用有所增加，但降低了配网失负荷的风险，并且在将敏感负荷损失量转化为相应经济损失后，综合投资费用从3 605.1万元下降至3151.0万元，提高了配网规划的经济性。因此在进行网架规划时，考虑电压暂降导致的敏感负荷损失量是合理且必要的。

5 结语

可再生能源发电受天气和季节的影响比较大，抗干扰能力较差，大量新能源接入电网，对电网电压产生大幅扰动。针对变频器接入型负荷的适应性，本文总结了多种主要敏感设备的电压耐受特性，建立了变频调速电机的仿真模型，并计算了变频调速器在VTC不确定区域内受电压波动影响的负荷损失概率。在原有风险规划的基础上，提出了考虑电压波动下敏感负荷损失的配电网规划模型，提高了规划方案的合理性。以6节点系统电网为例，利用粒子群算法对考虑敏感负荷损失的风险规划模型进行求解。与不考虑敏感负荷损失时的规划方案相比，降低了敏感负荷损失的风险，提高了配网规划方案的经济性。