MOA冲击电流模型的建模仿真及试验研究

姚亚鹏， 刘崇新， 庄建煌

(1. 电力设备电气绝缘国家重点实验室(西安交通大学)，陕西 西安710049；2. 国网福建省电力有限公司莆田供电公司，福建 莆田351100)

0 引言

金属氧化物避雷器(metal oxide arrester，MOA)的电气性能优异，是限制雷电过电压、操作过电压和保护其他的电气设备免受过电压损害的重要设备[1-6]，在电力系统过电压防护中应用十分广泛。在MOA投入使用前对其进行出厂试验或验收试验时，须采用产生指数波的冲击电流发生器对MOA进行冲击残压试验来模仿雷电流对保护设备的破坏作用，检验电气设备耐受冲击电流的稳定性。仿真过程中，正确有效地建立雷电流模型对MOA的特性分析和模拟计算的准确性具有重要意义。

雷电流波形具有偶然性、随机性和不规则等特点，长期大量研究得出雷电流共有特征为大部分的雷电流都是短时电流，且大部分短时雷电流的形式是单极性脉冲等。结合前人观测数据，通过实验等方式，多种雷电流模型被提出[7-14]。1941年，Bruce和Golde提出了双指数模型[7]，这是首次被提出的雷电流模型，也是目前应用较为广泛的模型，但该函数表达式中参数物理意义不明确，且在t=0时没有连续可导的一阶导数。为避免在t=0时刻导数的不连续性，很多学者针对Bruce提出的双指数模型进行了修正，Jones，Gardner和Raicic等人先后提出了多种修正函数[8,10]，但由于参数计算复杂度及雷电流特征量的差异使其在工程应用中不是很广泛。1969年，Uman和Mclain[9]提出了传输线模型；1985年，Heidler提出了新的函数模型并对模型参数确定[10]进行了分析；1987年，Rakov和Dulzon对TL模型进行了修正提出了MTLL模型；之后，Nucci等人对TL模型修正提出了MTLE模型；1995年国际电工委员会在IEC 62305-1文件[11]中规定Heidler函数为仿真雷电流的模型。1998年，Rokov和Uman[12]将当前雷电流模型分为4类，并对4类模型做了详细定义和阐述；2000年，Rouzbeh Moini等人[13]基于天线理论提出AT模型，与已有的多种模型进行了对比分析，所得波形变化规律与观测数据相符。2002年，张飞舟和刘尚合学者[16]针对闪电回击电磁场提出了一种新的脉冲函数模型；2009年，Rokov等人对雷电研究及防护进行了总结分析[15]，从雷电放电观测、雷电放电模型、雷电发生特性/雷电定位系统、雷电电磁脉冲、雷电感应效应及防护等5个方面进行了较为详细的分析研究。2011年，Javor和Rancic[14]提出了一种新的雷电回击基电流函数(new channel-base current，NCBC)模型，输出波形与国际标准IEC 62305-1相符。2015年，Andreotti和 Verolino[17]提出了新的基电流分段函数模型，满足标准雷电流波形主要特性。

国内外关于雷电分析的研究成果较为丰硕，由于以上雷电流函数模型有确切的表达式，即输出波形不受负载非线性影响，而在MOA实际冲击电流试验中，采用的冲击电流发生装置需要根据负载情况适当调节回路参数以产生满足工程需要的波形，在仿真分析中直接采用雷电流函数模型代替冲击电流回路来研究MOA的非线性特性，忽略了电流波形的差异对负载特性的影响。文中主要针对MOA冲击试验中冲击电流装置冲击电流模型进行分析，选取了3种常用的雷电流函数模型，分析了冲击电流发生回路与上述雷电流模型的基础理论，在ATP-EMTP及MATLAB/Simulink软件中搭建冲击试验回路，结合试验数据进行仿真分析。仿真结果表明，选取不同的雷电流函数模型会对仿真结果造成明显的差异，雷电流对负载特性的影响不容忽略。

1 雷电流模型

1.1 双指数函数模型

双指数函数(double-exponential function, DEXP)模型作为首次被提出的雷电流模型，应用较为广泛，其函数表达式如下。

(1)

式中：I0为电流峰值；α，β分别为决定上升时间和衰减时间及电流最大陡度的时间常数；η=e-αTm-e-βTm表示峰值修正系数，其中Tm为峰值时间，可通过对函数求一阶导数得出，Tm=ln(β/α)/(β-α)。将电流幅值的50%时对应的时间T50代入式(1)，有Im/2=I0/η(e-αT50-e-βT50)。由此可知，由特定的参数I0，α，β可绘制出相应的电流波形图，并得到对应的波形参数。

1.2 Heidler函数模型

Heidler所提雷电基电流函数表达式如下[10,18]。

(2)

式中：I0，τ1，τ2和n为可调节参数，τ1，τ2分别为上升时间和衰减时间常数；n为电流陡度系数，η=e-τ1/τ2(nτ2/τ1)1/(n+1)表示峰值修正系数。

1.3 脉冲函数模型

采用函数-脉冲函数模型(pulse function)来表示闪电回击电流，可以避免双指数函数在t=0时刻一阶导数过大且不连续及Heidler函数不可积、 雷电电磁脉冲(lightning electromagnetic pulse, LEMP)数值计算麻烦的问题。

(3)

通过调节参数I0，n，τ1，τ2亦可得到所需波形。

2 MOA冲击电流发生回路

在对MOA进行出厂试验或是验收试验时，须采用冲击电流发生器产生特定指数波冲击电流进行残压试验。指数波冲击电流回路可简化为RLC放电回路，基于线性负载的研究现已有较为成熟的理论基础，而对于带有不可定量确定的非线性负载的冲击电流回路的设计常基于线性负载设计理论进行改进，以满足工程需要。

2.1 带线性负载放电回路的理论分析

图1为指数波冲击电流装置主放电回路，C为许多并联电容器的电容总值，L及R为包括电容器、回路连线、分流器、球隙和负载的电感和电阻值。结合电路理论可得式(4)。

图1 冲击电流装置主放电回路Fig.1 Main discharge circuit of impulse current device

(4)

公式(4)是一个二阶常系数齐次微分方程，将其转换为特征方程，并求其特征根，根据特征根量值分3种情况进行分析。

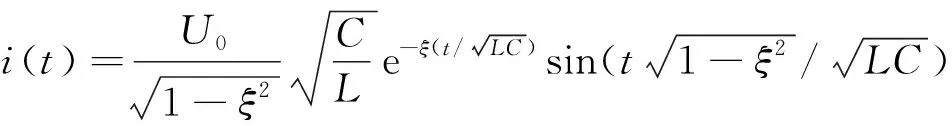
(5)

式(5)输出波形为振荡波，对其求导可得:

(6)

为更好地分析阻尼系数与冲击电流发生波形的关系，对式(5)进行归一化，i*，t*分别为归一化冲击电流参数和归一化时间参数。将式(7)和(8)代入式(5)可得式(9)。

(7)

(8)

(9)

(10)

(11)

i*=t*e-t*

(12)

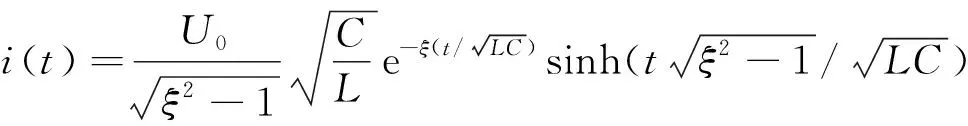
(13)

(14)

(15)

2.2 带线性负载放电回路的仿真与设计

由以上冲击电流回路基础理论分析可知冲击电流波形与阻尼系数的关系，采用MATLAB语言可编程绘制出阻尼系数与输出波形的关系曲线，根据IEC和国标对不同波形容许偏差的要求绘制阻尼系数与各波形参数间的曲线。在仿真过程中，可采用以下公式对波前时间T1、半峰值时间T2进行计算。

(16)

(17)

式中：T10，T50，T90分别为电流幅值的10%，50%，90%时对应的时间,且这些数值可直接测得。

(18)

实际工程中可根据波形参数容许误差选取合适的阻尼系数和归一化波形参数值，进而通过计算求得放电回路各线性元件值。根据IEC和国标规定，8/20s、10 kA的冲击电流波的容许偏差范围为：峰值im(±10%)，波前时间T1(±10%)，半峰值时间T2(±10%)，反极性振荡幅值/峰值im2/im1(<20%)。

图2(a)为根据其反极性振荡要求选取合适的阻尼系数范围ξ>0.455 9，图2(b)为根据半峰值时间与波前时间之比在工程容许偏差范围内选定阻尼系数的范围0<ξ<0.662，结合这两个范围进一步确定输出波形满足工程需要的阻尼系数取值范围为0.455 9<ξ<0.662。图2(c)-(d)分别为T1*和im*与阻尼系数的关系曲线，阴影部分为满足实际工程需要的取值范围，选定某一阻尼系数值通过式(7—8)可得各线性元件值。

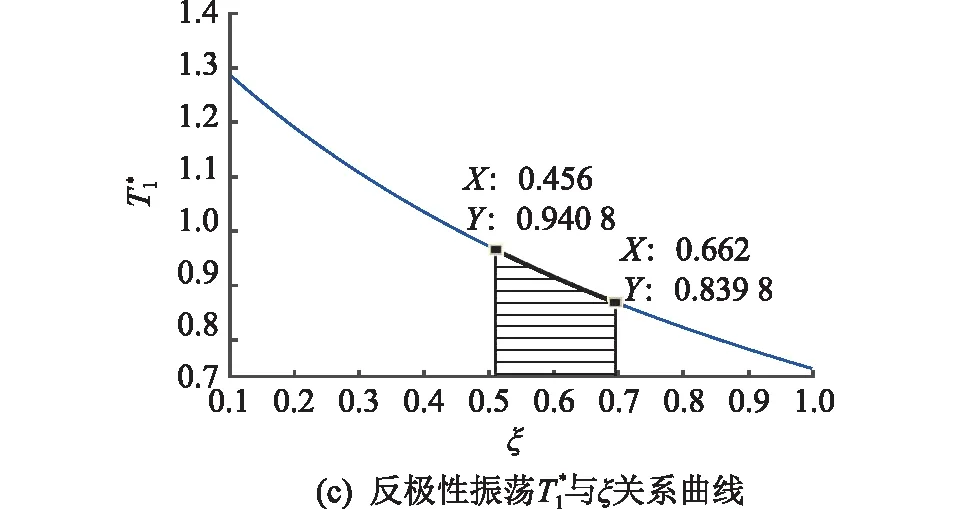
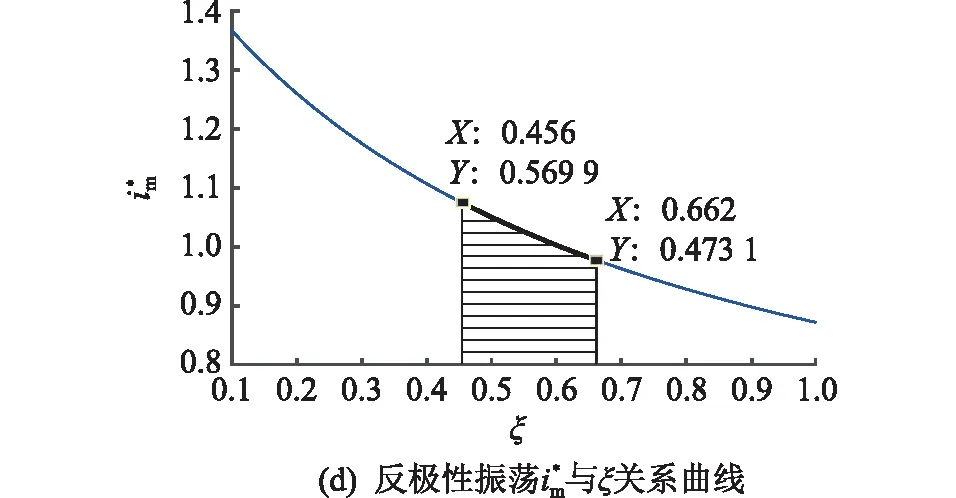
图2 波形参数与关系曲线Fig.2 The curve between waveform parameter and ξ

图3 8/20 s、10 kA冲击电流回路仿真Fig.3 Simulation waveform

表1 8/20 s、10 kA冲击电流回路仿真结果Tab.1 Simulation results

表1 8/20 s、10 kA冲击电流回路仿真结果Tab.1 Simulation results

2.3 MOA放电回路仿真设计

针对负载为非线性电阻(MOA、压敏电阻片等)冲击电流回路的研究，现有两种较为常见的设计方法。(1) 在已知MOA结构系数和非线性系数的前提下，选定在某一冲击电流幅值点的等效动态电阻作为设计依据，将冲击电流回路设计在临界阻尼状态，再在回路中加入适量的线性调波电阻，进而得到符合标准要求的波形。(2) 未知负载参数时，通过冲击电流试验得到负载动态电阻变化范围，采用线性调波电阻的理论进行设计[19-24]。文中基于现有理论，采用冲击电流试验中发生器的参数搭建仿真回路，根据实际试验数据来模拟MOA伏安特性。

3 仿真与试验结果分析

文中主要针对MOA冲击电流残压试验进行仿真研究，搭建冲击电流试验仿真电路，通过不同冲击电流波形(雷电波8/20s,操作波30/80s, 陡波1/5s)确定上述各雷电流模型参数，并绘制出相应的电流、残压波形。金属氧化物避雷器电阻片(metal oxide varistors, MOV)试品参数数据为：尺寸(直径×高度) 42×24 mm，标称放电电流10 kA，额定电压3.67 kV，8/20s、10 kA冲击电流下残压8.85 kV， 30/80s、500 A冲击电流下残压6.93 kV，1/5s、10 kA冲击电流下残压10.02 kV。以雷电波冲击电流波形为8/20s、幅值10 kA为例进行分析研究，其试验波形如图4(a)所示。

在ATP-EMTP软件中搭建电路，MOV伏安特性选用type-92来建模，根据已知样品数据用分段线性的V-I点组成伏安特性曲线。由于ATP-EMTP软件中type-92模型实质上采用最小二乘法进行拟合，拟合目标函数公式为i=p(v/vref)q，p，q为电阻片特性系数，vref为任意基准电压，可防止指数运算时数据溢出(取vref=10 kV)。为尽可能准确的表示该样品的非线性特性，根据已知数据点设置容许误差对其拟合求出目标函数表达式，采用曲线拟合工具求出此时的p=4.466×104，q=12.25。

遵照GB 11032—2010交流无间隙金属氧化物避雷器要求进行冲击电流残压试验，试验波形如图4(a)所示。采用RLC冲击电流回路仿真波形如图4(b)所示。由于波前时间T1和半峰值时间T2不可直接测得，须通过公式(16—17)进行计算得出，对于雷电流函数模型，可以将峰值时间Tm，T10，T90或T50及对应电流值代入函数，根据电流波形容许偏差求出函数波形调节参数。

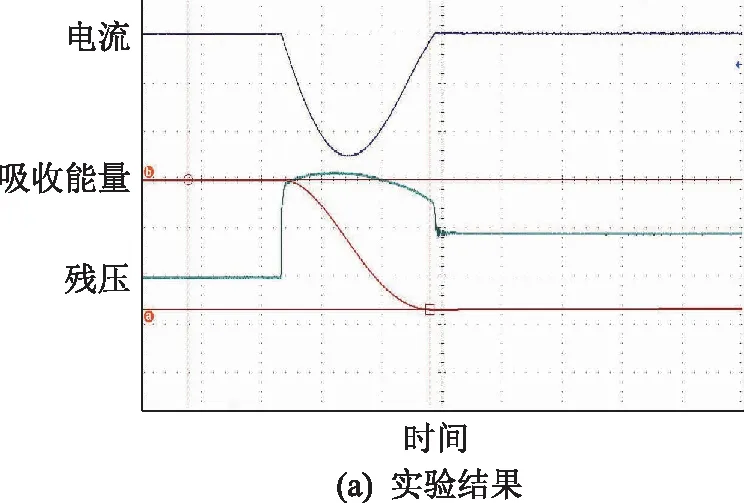
图4 MOA 8/20s、10kA试验与仿真结果Fig.4 The measured and simulated waveforms

由于ATP-EMTP软件中不支持以上部分函数模型仿真研究，文中在MATLAB/Simulink中搭建仿真电路，MOA特性通过引入上述计算所得参数进行模拟。表2为8/20s、10kA冲击电流下上述3种雷电流函数模型的选取参数。

表2 8/20 s、10 kA下雷电流函数模型参数Tab.2 The parameters of lightning current model

表2 8/20 s、10 kA下雷电流函数模型参数Tab.2 The parameters of lightning current model

结合图5中曲线及表3中数据可知，在不同雷电流函数模型的激励下，8/20s、10 kA雷电流残压值结果近似相等，吸收能量值结果各异；即不同的雷电流函数模型输出波形的微小差异对残压值不会造成较大影响，而在计及吸收能量时，累积误差使得最终结果偏差较大。在以往的研究中，吸收能量值相对误差不能较好地用来证明MOA动态模型模拟的准确性。因此，选择并建立正确的雷电流模型对研究MOA动态模型较为关键。

图5 8/20s、10 kA下各模型仿真波形Tab.5 Simulation waveforms of different models

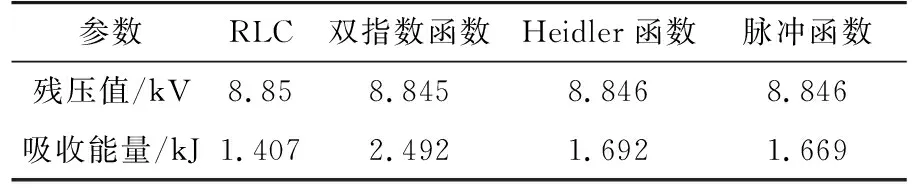
参数RLC双指数函数Heidler函数脉冲函数残压值/kV8.858.8458.8468.846吸收能量/kJ1.4072.4921.6921.669

在上述3种模型选取参数时，双指数函数模型在保证波前时间满足工程需要的前提下，半峰值时间不能满足要求，函数参数没有严格的物理意义，选参较为复杂且不易调节，而Heidler函数和脉冲函数可输出较为满意的波形。

4 结论

文中主要针对MOA冲击试验中冲击电流装置冲击电流模型进行分析，选取双指数函数模型、Heidler函数模型、脉冲函数模型，分析了冲击电流发生回路与上述雷电流模型的基础理论，基于ATP-EMTP 和MATLAB/Simulink搭建冲击试验回路，结合试验数据进行仿真分析，并给出了ATP-EMTP软件中常用模型的波形参数。研究结果表明：

(1) 双指数函数参数由于没有严格物理意义，选参较为复杂；Heidler函数模型和脉冲函数模型可通过调节参数输出较为满意的波形，且在模拟MOA残压试验时，模拟结果相对较为准确。

(2) 不同的雷电流函数模型输出波形的微小差异对残压值不会造成较大影响，而在计及吸收能量时，累积误差使得最终结果偏差较大。在以往的研究中，吸收能量值相对误差不能较好地用来证明MOA动态模型模拟的准确性。